-
用电负荷是电力系统规划设计和运行管理的最重要的指标之一[1],受许多因素的共同影响,在极端天气条件下天气气候的影响尤为重要[2]。由于用电负荷与气象条件和气象因子的变化有很大关系[3-4],气象因子是影响电力系统负荷预测的重要因素,可引起30%左右的电力负荷上升[5]。气象因子在短期负荷预测中应用十分广泛[6-7],众多学者基于气象条件的用电负荷预测方面做了许多有意义的工作。很多学者研究了中国不同区域、不同时段气象条件与用电负荷的关系[8-9],还考虑了气象综合指数和气温等要素的累积效应[10]。但由于气候条件、经济结构和发展水平的不同,各电网电力负荷与气象因子的关系也不尽相同[11];因此,研究气象与用电负荷的关系对负荷预测的工作具有重要意义。
准确高效的短期用电负荷预测是保证电力系统安全可靠运行的前提,也是电网合理安排发电计划的依据。由于电网系统是一个复杂的、非线性的耦合系统,用电负荷的时间序列一般也具有非线性、非平稳的特点[12]。因此,用电负荷预测方法和模型的构建引起了众多学者的极大关注。以往的用电负荷预测的方法主要包括自回归法[13]、支持向量机法[14]、神经网络法[15],也有基于波动模型[16]、模糊逻辑[17]、递归数字滤波器[18]、专家系统等方法。但传统方法一般忽略了电网具有的随机、突发等特性,导致预测结果与实际需求有一定的差距。随着深度学习算法的快速发展,一些专家学者利用BiLSTM神经网络、长短时记忆LSTM(Long Short-Term Memory)神经网络等方法在用电负荷预测中进行了探索[19]。这类神经网络学习方法的优势在于,不需要对输入变量做复杂的假设,可以模拟多个变量;利用输入变量在训练过程中,通过学习来抽取和逼近隐含的输入和输出变量之间非线性关系。
我国华北地区相对干旱少雨,常出现用电紧缺现象,夏季持续高温造成电网用电负荷屡创新高。2022年8月6日,石家庄市最大日用电负荷高达9.634 GW,为近10 a历史最高值,且8月3~6日,连续4 d日用电负荷最大值超过9.4 GW,分别为9.425 GW、9.444 GW、9.571 GW、9.634 GW,给电网用电负荷预测带来前所未有的压力。本文以石家庄为例,揭示中国华北地区主要城市过去10 a的用电负荷与气象条件的关系,并引入相对危险度分析得出二者之间的定量关系,并基于此探讨一种日用电负荷峰值的预测方法,以期为改进和完善电力负荷短期预测方法提供参考和指导。
-
本文所用用电负荷数据来自于国网河北省电力公司,时间长度自2013年1月1日至2022年12月31日,时间间隔为逐15 min,选取每日最大值作为日最大电力负荷,采用比较滤波法对逐日最大负荷数据进行质量控制。所用气象数据来自于河北省气象大数据云平台,包括石家庄站(53698站)日最高气温、最低气温,日最小相对湿度,日最大风速、平均风速,过去24 h变温,08~次日08时24 h、48 h、72 h累计降水量。时段与用电负荷数据时段一致,且经过严格的质量控制。
-
用电负荷的构成包含3个方面[20]:
$$ L={L}_{{\mathrm{t}}}+{L}_{{\mathrm{m}}}+\varepsilon $$ (1) 式中:
$ {L}_{{\mathrm{t}}} $ ——受经济发展影响的基础负荷,也叫经济负荷;
$ {L}_{{\mathrm{m}}} $ ——受气象因素影响的气象敏感负荷;
$ \varepsilon $ ——随机分量,包含节假日效应、工业检修、电网调价等不确定因素。
在本研究中,针对随机分量$ \varepsilon $,受资料限制,个别因工业检修、电网调价等不确定因素未考虑,且根据本文分析和已有研究得知,除劳动节、国庆节、春节等假期明显影响电力负荷以外,普通小长假和周末对日用电负荷最大值影响较小。
剔除用电负荷奇异值后,计算当天日用电负荷最大值与前1天日用电负荷最大值的差值,并将其作为当天日最大用电负荷峰值的变化幅度$ \Delta L $(简称变幅),因经济负荷$ {L}_{{\mathrm{t}}} $在一段时间内相对固定,因此$ \Delta L $可视为气象条件引发的日用电负荷最大值的变幅,本文共得到有效的$ \Delta L $样本3649个。在分析用电负荷分布特征时,选取全部有效样本进行分析。在分析气象条件引发的日用电负荷最大值变幅时,只选用剔除随机分量(重污染导致限产日的数据和劳动节、国庆节、春节期间假期首日及增幅明显日数据)影响后的3593个样本。
-
本文采取Tom提出的、由Boserl进一步发展的温湿指数计算方法,综合考虑气温和相对湿度的影响,其具体计算公式为:
$$ {E}_{{\mathrm{t}}}={T}_{{\mathrm{d}}}-0.55\times (1-R)\times ({T}_{{\mathrm{d}}}-58) $$ (2) 式中:
$ {T}_{{\mathrm{d}}} $ ——干球气温(°F);
R ——相对湿度(%);
$ {T}_{{\mathrm{d}}} $ ——华氏温度利用公式,$ {T}_{{\mathrm{d}}}=T\times \dfrac{9}{5}+32 $计算;
T ——气温(℃)[21]。
-
由于日最大用电负荷变幅及部分气象要素可能为非正态分布,在相关分析时,采用Spearman秩相关方法[22]。Spearman秩相关方法也叫Spearman等级相关系数法,是一种非参数检验方法。对于n对观察数据$ \left({{x}}_{{i},\;}{{y}}_{{i}}\right)({i}=\mathrm{1,2},\cdots {n}) $,按照每组变量n个数据的大小次序,分别由小到大编上秩次,对重复数据取平均等级,再检验2组变量的等级或秩次之间是否相关。通常用秩相关系数$ {r}_{\mathrm{s}} $表示,其值介于−1~1之间,$ {r}_{\mathrm{s}} $是正值时表示正相关,$ {r}_{\mathrm{s}} $是负值时表示负相关。其表达式为:
$$ {r}_{{\mathrm{s}}}=1-\dfrac{6}{n\left({n}^{2}-1\right)}\displaystyle \sum\limits _{i=1}^{n}({R}_{i}{-{Q}_{i})}^{2} $$ (3) 式中:
n ——时间序列的长度;
$ {R}_{i} $、$ {Q}_{i} $ ——$ {x}_{i} $和$ {y}_{i} $的秩次。
利用T检验法检验$ {r}_{{\mathrm{s}}} $的显著性,计算公式为:
$$ t={r}_{{\mathrm{s}}}\sqrt{\dfrac{n-2}{1-{r}_{{\mathrm{s}}}^{2}}} $$ (4) -
在分析日最大用电负荷与气象条件定量关系时,主要分析不同气象要素引发的日最大用电负荷的相对危险度,相对危险度(Relative Risk,RR)表示气象要素每发生单位变化,对应日最大用电负荷的相对改变量。利用泊松分布和平滑曲线拟合,采用R语言及EmpowerStats统计分析软件计算日最大用电负荷相对危险度,并进行气象要素对日最大用电负荷的响应分析[23]。以日最大用电负荷作为因变量,以相关气象要素为自变量,挖掘日最大用电负荷与气象因子的关联关系。两者的对数关系为:
$$ {\mathrm{ln}}\left[E\left({{Y}}\right)\right]=\beta X+\alpha $$ (5) 式中:
$ E\left({{Y}}\right) $ ——日最大用电负荷的期望值;
$ X $ ——气象影响要素;
β、α ——系数、截距,均通过秩相关分析得来。
$$ {\mathrm{RR}}={\mathrm{EXP}}(\beta \Delta X) $$ (6) 当RR>1(β>0)时,随着X每增加1个单位,$ Y $的发生风险也相对增加,增加率为(RR−1)×100%;同理,RR<1(β<0)时,随着$ X $每增加1个单位,$ Y $的发生风险相对减小,减小率为(1−RR)×100%。
-
首先选取与日用电负荷峰值相关性显著的气象要素,计算因不同气象要素发生单位变化所引发的日用电负荷峰值的变化率($ \Delta {{\mathrm{RR}}}_{i} $),即不同气象要素对日用电负荷峰值的相对危险度。其次根据日用电负荷峰值的变化率以及实时的气象要素数据,计算得出由所有显著性相关的气象要素所引发的次日用电负荷峰值累积变化量$ {\Delta L}_{{\mathrm{m}}} $,即因气象条件所引发的次日用电负荷峰值变化量。然后计算节假日用电负荷随机分量$ \varepsilon $,计算每年节假日中的日用电负荷明显下降日和日用电负荷明显上升日这两日的日用电负荷峰值变化量的中位数,将其作为该年度的主要节假日用电负荷随机分量。经统计,近10 a节假日用电负荷随机分量的中位数为270 MW,占前1日用电负荷峰值的2%~5%。最后根据当日用电负荷峰值数据和当日气象要素观测数据以及次日气象要素预报数据、主要节假日用电负荷随机分量,计算次日用电负荷峰值$ {L}_{{\mathrm{max}}(t+1)} $。
$$ {\Delta L}_{{\mathrm{m}}}={L}_{{\mathrm{max}}\left(t\right)}.\displaystyle \sum\limits _{i=1}^{m}\left[{X}_{i(t+1)}-{X}_{i\left(t\right)}\right]\Delta {{\mathrm{RR}}}_{i}/{{m}}_{i} $$ (7) 式中:
$ {\Delta L}_{{\mathrm{m}}} $ ——受气象因素影响的用电负荷变化量;
$ {L}_{{\mathrm{max}}\left(t\right)} $ ——当日用电负荷峰值;
$ {X}_{i(t+1)} $ ——某气象要素次日预报值;
$ {X}_{i\left(t\right)} $ ——该气象要素当日实况值;
$ {m}_{i} $ ——单位变化,气温和风速分别取1,温湿指数取100,降水量取10。
$$ {L}_{{\mathrm{max}}(t+1)} = {L}_{{\mathrm{max}}\left(t\right)} + {\Delta L}_{{\mathrm{e}}} + {\Delta L}_{{\mathrm{m}}} + \varepsilon $$ (8) 式中:
$ {L}_{{\mathrm{max}}(t+1)} $ ——当日用电负荷峰值;
$ {\Delta L}_{{\mathrm{e}}} $ ——受经济发展影响的基础用电负荷变化量;
$ \Delta {L}_{{\mathrm{m}}} $ ——受气象因素影响的用电负荷变化量;
$ \varepsilon $ ——主要节假日用电负荷随机分量;
$ {\Delta L}_{{\mathrm{e}}} $ ——受经济发展影响的基础用电负荷变化量,本文指次日基础用电负荷与当日基础用电负荷的差值,连续两日,视为经济发展影响的基础负荷不变即相等,所以$ {\Delta L}_{{\mathrm{e}}}=0 $。
-
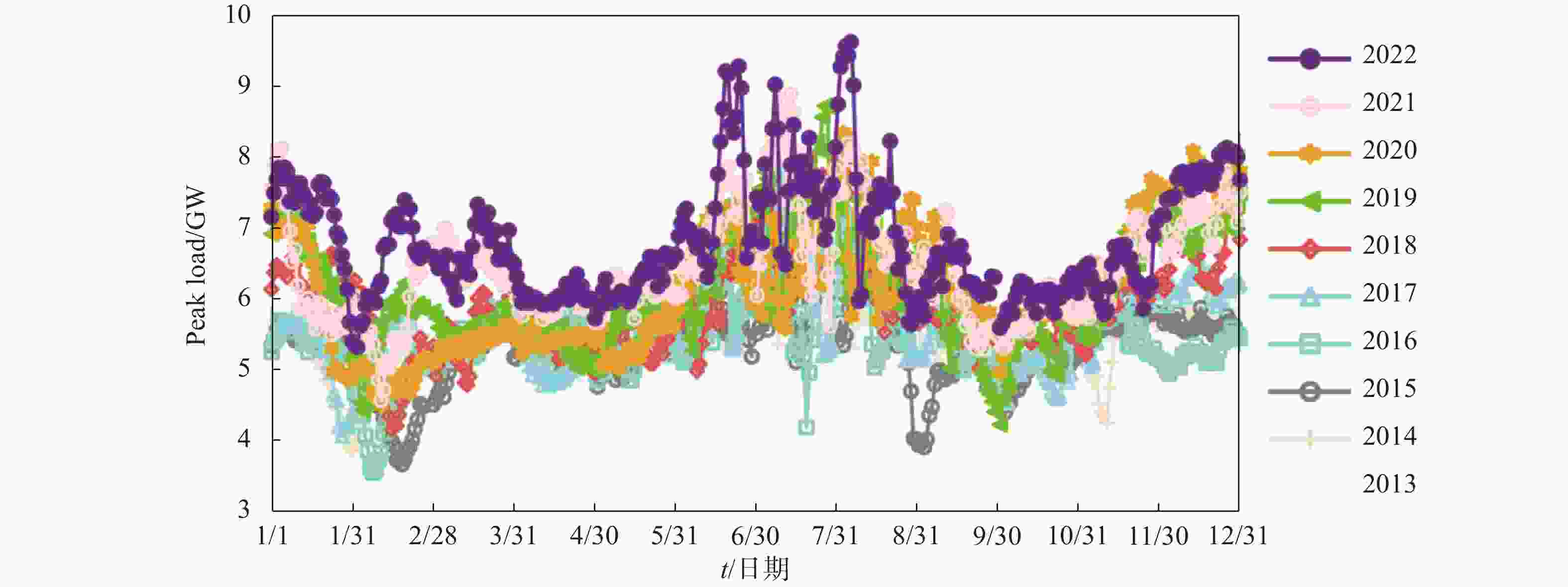
从2013~2022年日用电负荷峰值的时序图(图1)可见,石家庄市过去10 a用电负荷呈增长的趋势。2013年石家庄市逐日用电负荷峰值平均为5.451 GW,2022年增长为6.81 GW,增长近25%;这种用电负荷峰值显著增长的趋势与社会经济发展和人们生活水平提升密不可分。同时,年度负荷呈“双峰双谷”型分布,高峰出现在夏季6~8月,7月最高,次高峰出现在冬季11月~次年1月。低谷持续时间较短,主要出现在每年的2月和10月,基本对应春节和国庆节,工业用电量明显减小。这种双峰型分布特征主要是夏季降温能耗和冬季采暖能耗造成的,而降温和采暖往往是由气象因素引起的,这与前人的研究比较一致[24]。
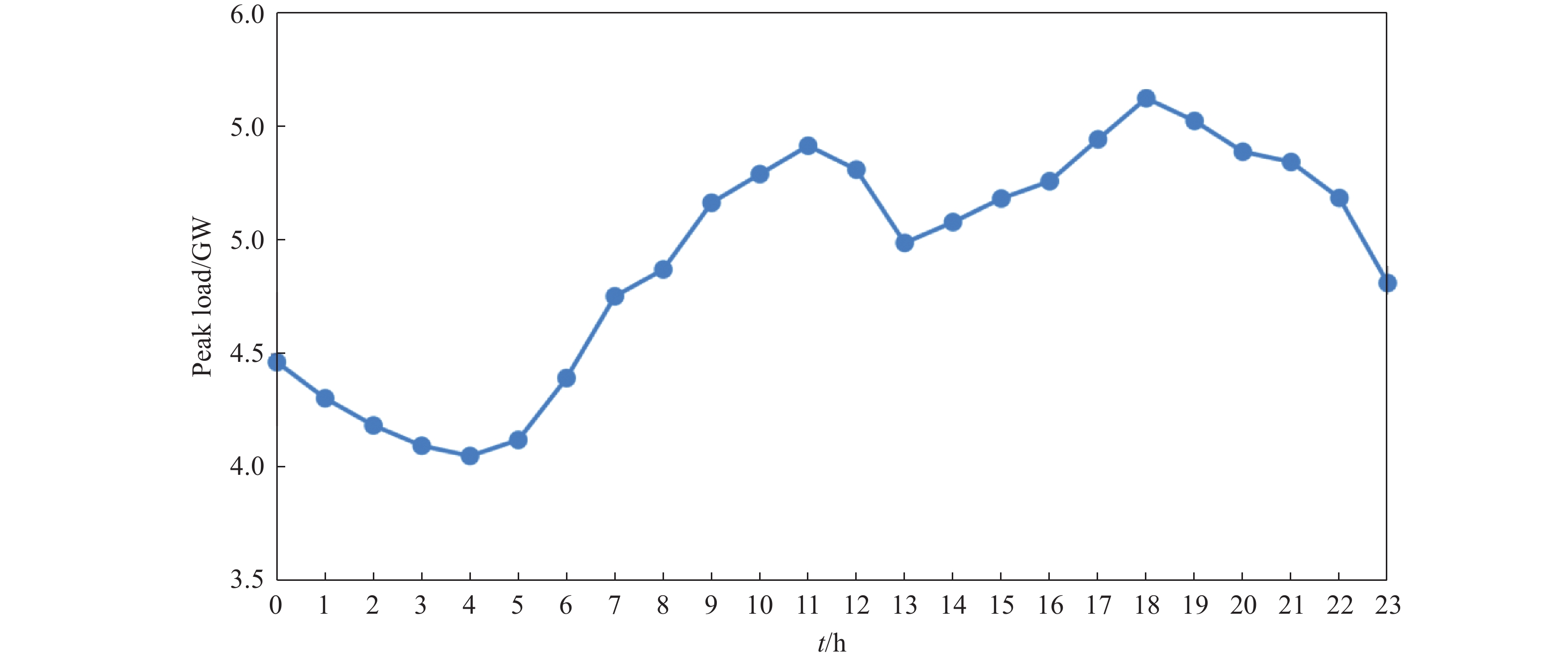
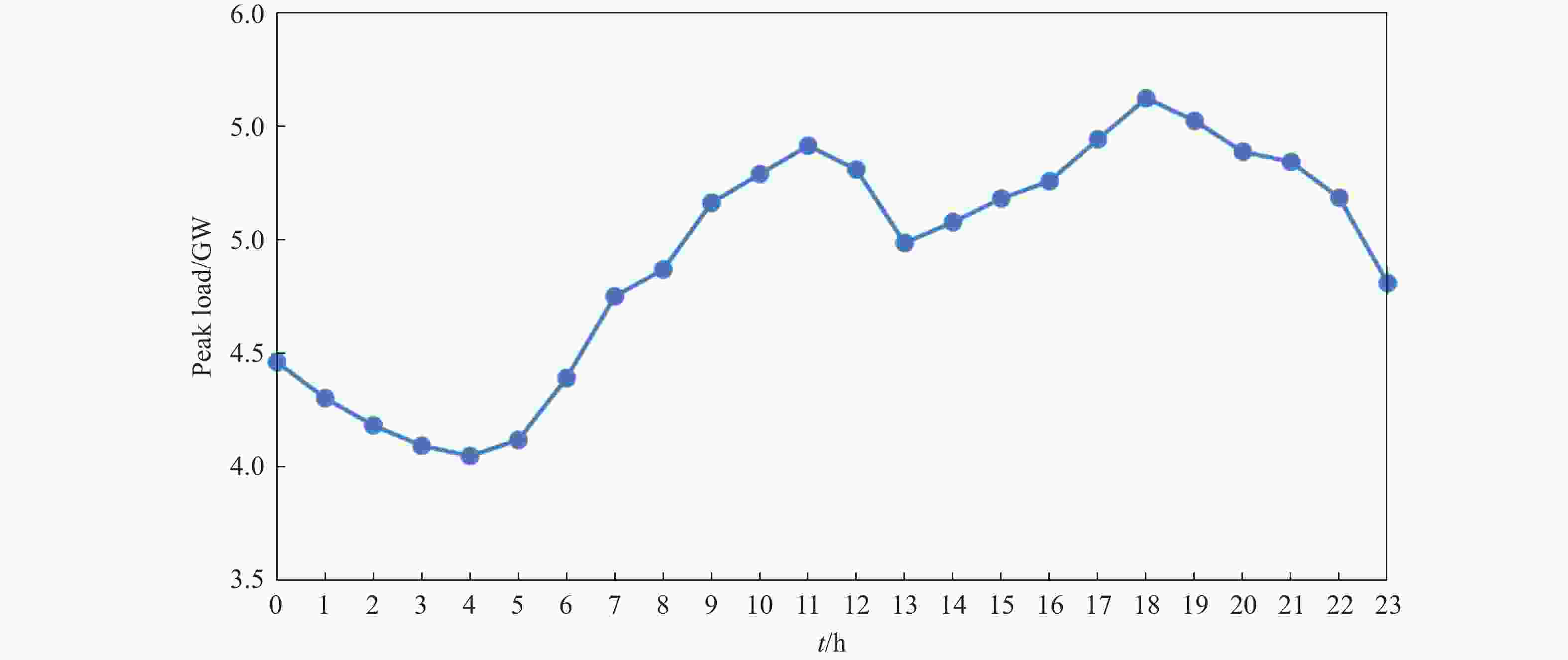
从过去10 a石家庄市用电负荷日变化曲线(图2)来看,在一天当中,用电负荷也呈现出“双峰双谷”型,但是波动范围不如月际之间波动大。早晨06时负荷开始增大,且06~08时之间增长幅度较大,各个时次较上1个时次的增长比例都在5%以上。上午11时达到一天中第1个峰值,之后出现“午间效应”,负荷开始降低,中午13时为白天时段最低。下午用电负荷再次上涨,到18时左右再次出现峰值,且这个峰值略高于上午11时。前半夜缓慢下降,22时~0时下降明显,降幅再次超过5%,之后平缓下降。有研究发现,负荷的日变化除受温度的影响之外,还受到居民生活习惯、电价等因素的影响。
-
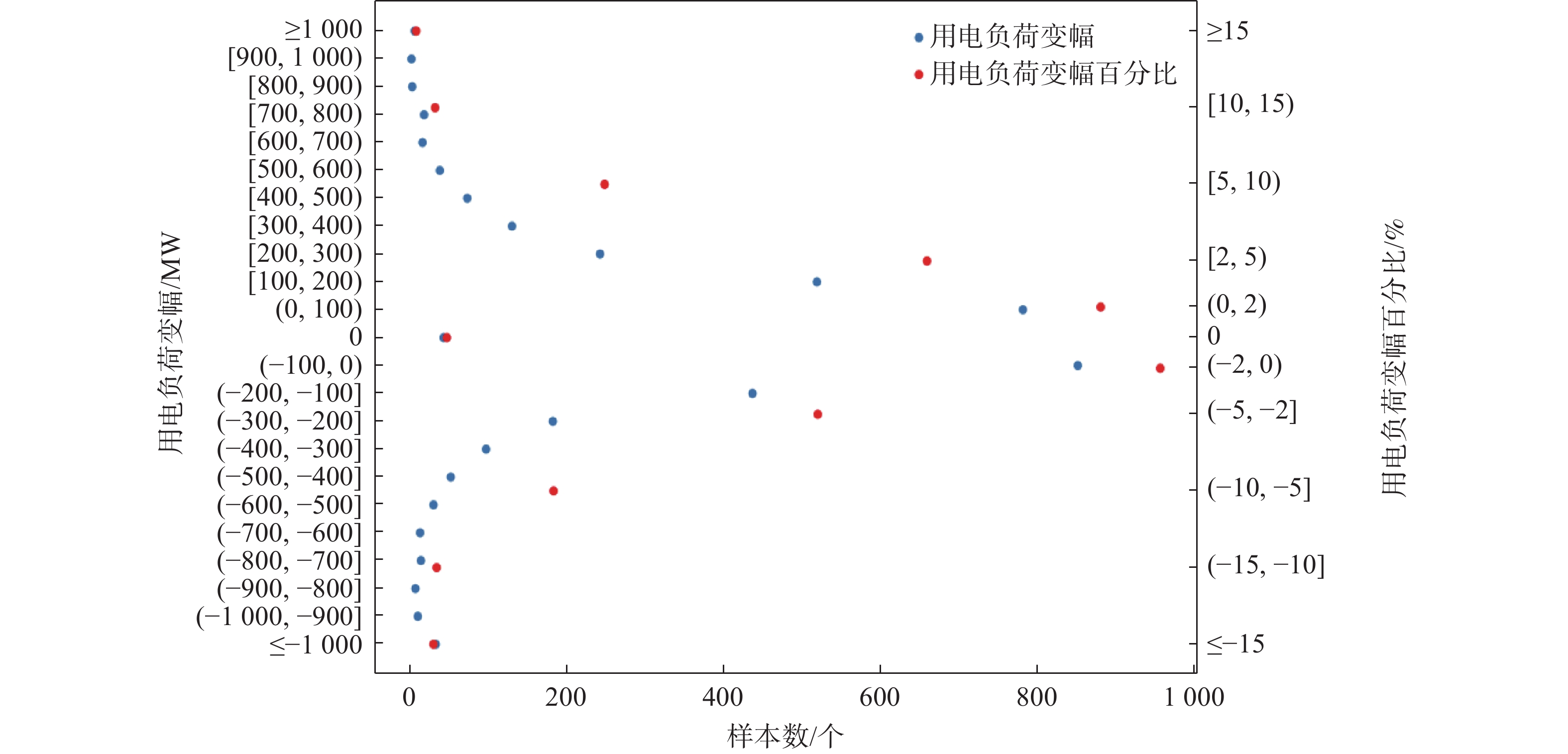
将$ \Delta L $与前1日用电负荷最大值作为日用电负荷变幅百分比,绘制日用电负荷变幅$ \Delta L $与日用电负荷变幅百分比的分布图(图3)。可见,共有2 627 d用电负荷变幅都处于±200 MW之间,占样本总数的73.11%;变幅在300~<500 MW的有776 d,占比为21.6%;500~<1 000 MW的有151 d,占比为4.2%;变幅超过1 000 MW的有39 d,占比为1.09%。
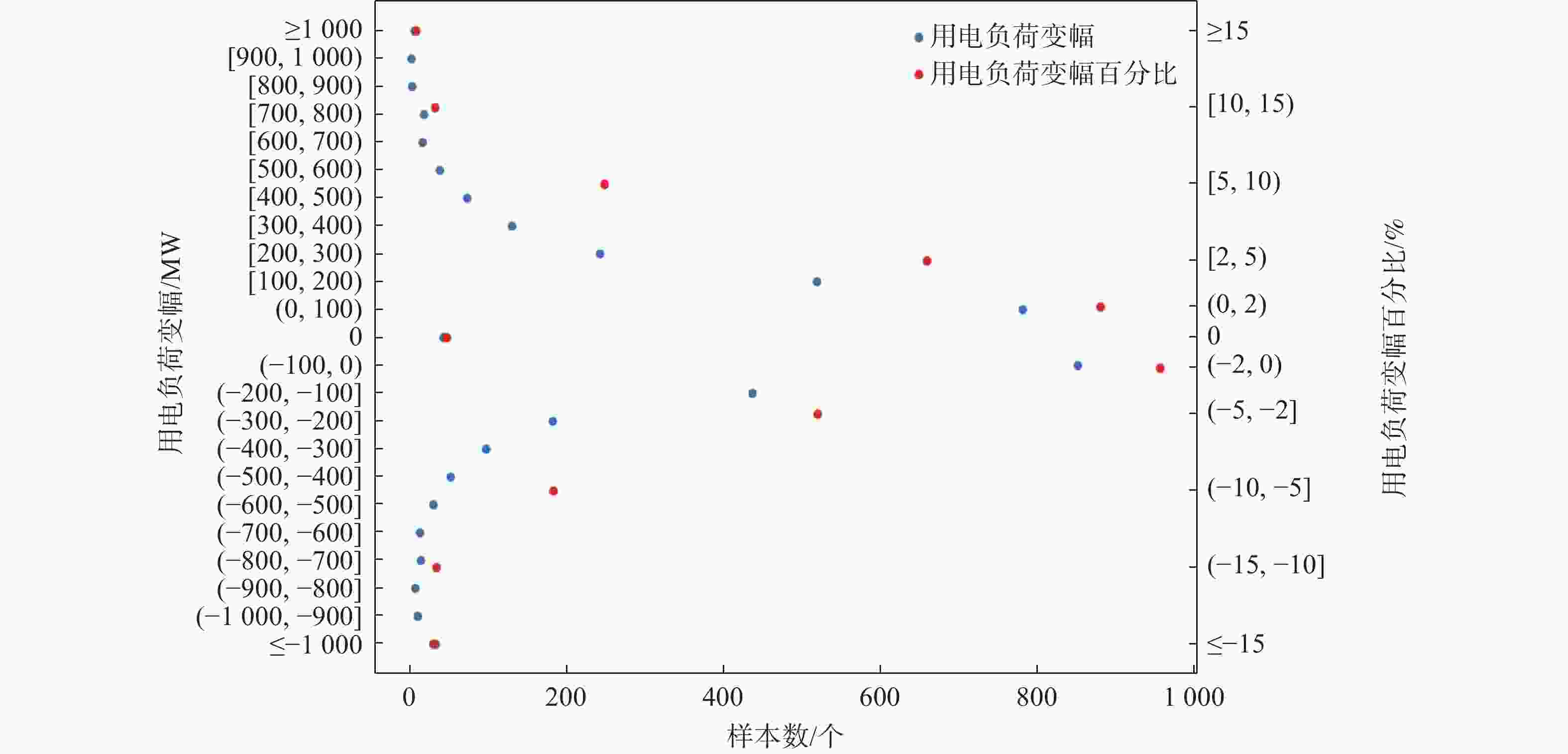
Figure 3. Distribution of amplitude variation of daily peak electricity load in Shijiazhuang from 2013 to 2022
变幅百分比处于±2%的占样本总数的52.35%,处于2%~5%的占32.76%,处于5%~10%的占12%,处于10%~15%的占1.84%,超过15%的占1.06%。其中增幅最大值为18.42%,降幅最大值为24.1%。通过查询气象条件发现,有62个样本出现在6~8月,有52 d对应出现明显降雨,中雨以上量级有26 d,有5 d对应前1日出现降雨。另有1 d对应出现大风。增幅超过10%的39次个例中,36 d出现在6~8月,其中12 d是前1天或前2天连续出现明显降雨,21 d是平均气温高于28 ℃且温湿指数在1 000以上,2 d是温湿指数不高但是最高气温较前期明显升高,另有1 d无明显特征。另外3次个例出现在11月和3月,对应明显降温或较大的负温湿指数。
分析过去10 a劳动节、国庆节和春节期间石家庄市用电负荷数据,发现假期首日用电负荷降幅百分比基本都超过5%,7 d长假基本在第3或第4天明显上涨,因此在下面的分析时将这部分数据作为“节假日效应”予以剔除。
-
采用Spearman秩相关方法计算2013年1月1日至2021年12月31日石家庄地区日用电负荷峰值与当日、前1日以及前2日气象条件的相关关系,发现日用电负荷峰值与前1日气象要素相关性最好(表1)。而其中日平均气温、日最高气温、日最低气温、日平均风速、日最大风速、温湿指数、降水量与日用电负荷峰值的相关系数通过了$ \alpha =0.01 $的显著性检验。气温和温湿指数对日用电负荷峰值的相关关系表现为春夏季呈正相关,夏季尤其显著,秋冬季呈负相关;气温和温湿指数与用电负荷峰值的季节相关性与前人的研究比较一致。风速整体呈现正相关,降水量呈现出负相关,冬季降水影响不如其他季节显著,但降水量和风速与用电负荷在不同月份的相关性差异较大,存在一定的不确定性。
气象要素 与日用电负荷峰值的秩相关系数 日平均气温 0.219 8** 日最高气温 0.214 1** 日最低气温 0.210 1** 24 h变温 −0.012 4 日平均相对湿度 −0.001 6 日最小相对湿度 0.021 4 温湿指数 0.213 2** 日平均风速 0.139 4** 日最大风速 0.158 7** 降水量 −0.271 3** 48 h累计降水 −0.092 6 72 h累计降水 −0.010 8 注:*表示通过0.05的显著性检验;**表示通过0.01的显著性检验。 Table 1. Rank correlation coefficient between daily peak electricity load and meteorological factors of the previous day in Shijiazhuang from 2013 to 2022
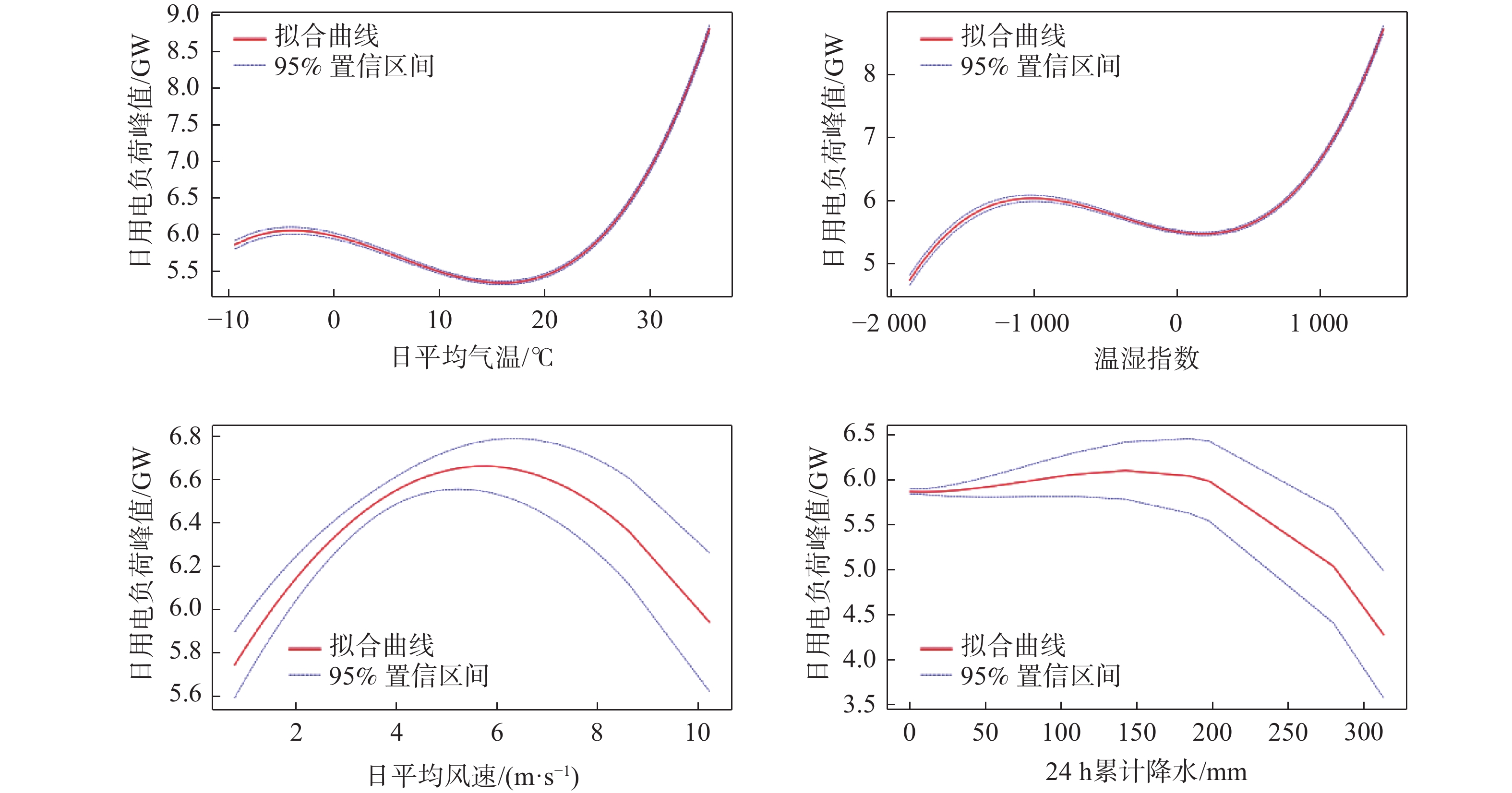
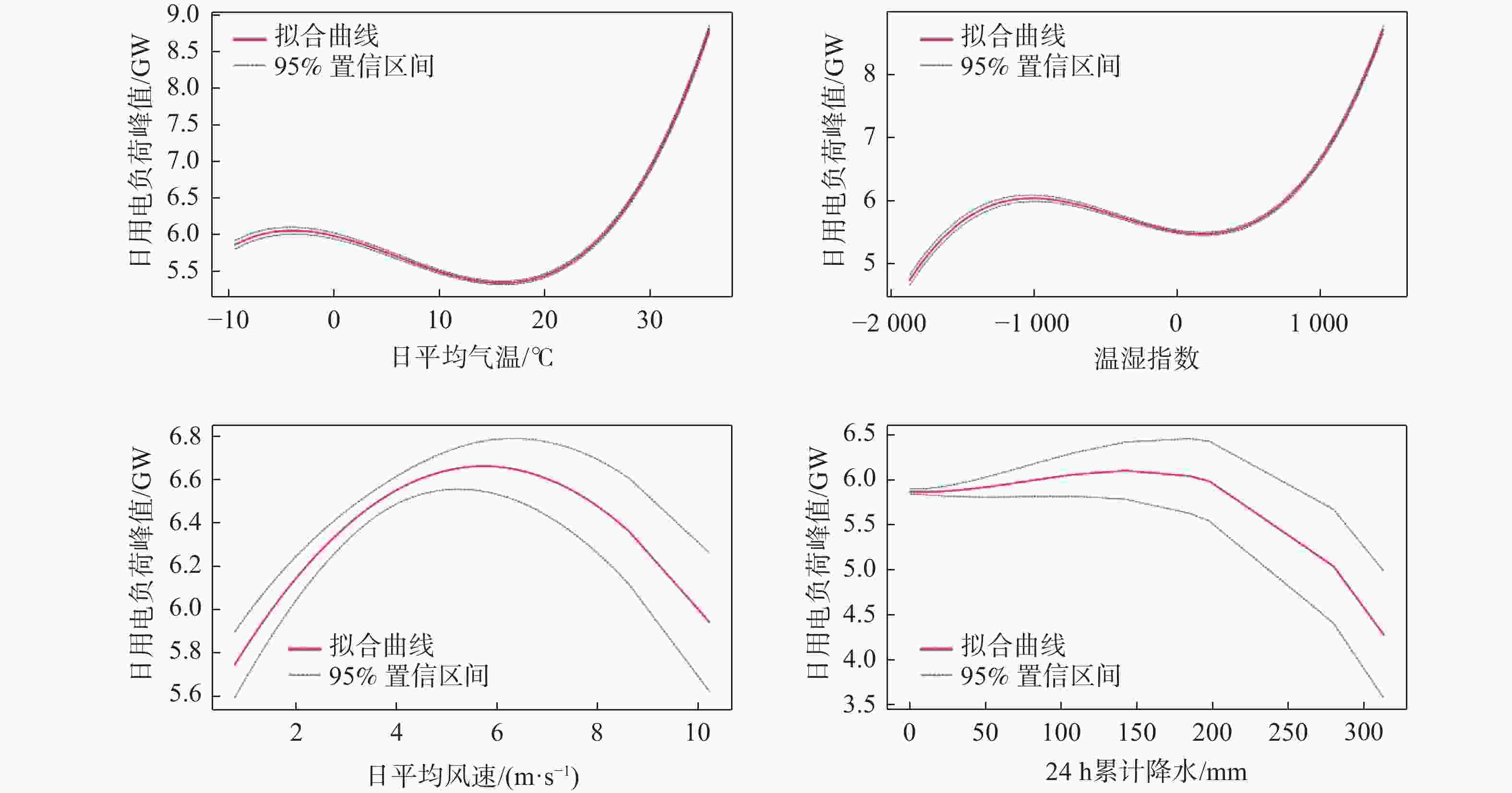
图4为石家庄地区过去10 a逐日用电负荷峰值与各气象要素的响应曲线,日用电负荷峰值对日最高气温、日最低气温与日平均气温的响应曲线趋势基本一致,对日最大风速与日平均风速的响应曲线趋势基本一致,因此略去部分图。可以看出,石家庄地区用电负荷峰值对日平均气温、温湿指数、日平均风速的响应曲线存在明显的阈值效应。日平均气温<16 ℃时,随着气温上升,日用电负荷峰值整体为减小趋势;日平均气温>16 ℃时,随着气温上升,日用电负荷峰值整体为上升趋势。日平均风速<5 m/s时,日用电负荷峰值随着风速的上升而减小,超过阈值时反之。温湿指数存在2个阈值,当温湿指数<−1 000时,随着温湿指数的增长日用电负荷峰值呈现增长趋势;当温湿指数处于−1 000和500之间时,日用电负荷峰值随着温湿指数的增长而下降;超过500时再次呈现<−1 000时的趋势,但是曲线陡度变大。随着累计降水量的增大,日用电负荷峰值呈现下降趋势,研究表明,有效降水对用电负荷的影响具有滞后性。
-
表2列出石家庄地区各气象要素对日用电负荷峰值变化的相对危险度。可以看出,日平均气温、日最高气温、日最低气温高于阈值时,每上升1 ℃,用电负荷峰值的相对危险度分别增加2.25%、1.92%、2.07%;低于阈值时,每上升1 ℃,用电负荷峰值的相对危险度分别减少0.62%、0.57%、0.60%。日平均风速达到5 m/s时,每上升1 m/s,用电负荷的相对危险度减少4.31%;日平均风速和日最大风速分别<5 m/s和10 m/s时,每上升1 m/s,用电负荷的相对危险度分别增加2.04%和1.98%,而高于阈值时,风速每增加1 m/s,用电负荷的相对危险度分别减少4.31%和2.44%。当温湿指数≤−1 000时,随着其发生100个单位变化用电负荷相对危险度增加3.66%,温湿指数在−1 000至500之间时,用电负荷相对危险度减少0.31%,温湿指数超过500时,对应用电负荷相对危险度增加4.22%。20~次日20时24 h累计降水量每增加10 mm,用电负荷相对危险度减少3.47%。
气象要素 阈值范围 相对危险度 95%置信区间 日平均气温 ≥16 ℃
<16 ℃1.022 5**
0.993 8**(1.021 4, 1.023 6)
(0.993 5, 0.994 1)日最高气温 ≥22 ℃
<22 ℃1.019 2**
0.994 3**(1.018 2, 1.020 1)
(0.994 0, 0.994 6)日最低气温 ≥12 ℃
<12 ℃1.020 7**
0.994 0**(1.019 6, 1.021 7)
(0.993 7, 0.994 3)日平均风速 ≥5 m/s
<5 m/s0.956 9**
1.020 4**(0.954 8, 0.959 0)
(1.019 3, 1.021 4)日最大风速 ≥10 m/s
<10 m/s0.975 6**
1.019 8**(0.975 4, 0.975 8)
(1.019 3, 1.020 3)温湿指数 ≥500
<−1 000<500
≤−10001.042 2**
0.996 9**
1.036 6**(1.040 1, 1.055 5)
(0.996 7, 0.997 0)
(1.035 9, 1.037 2)24 h降水量 >0 mm 0.965 3** (0.965 0, 0.965 9) 注:**表示通过显著性检验。 Table 2. Relative risk of meteorological factors to daily peak electricity load in Shijiazhuang from 2013 to 2022
-
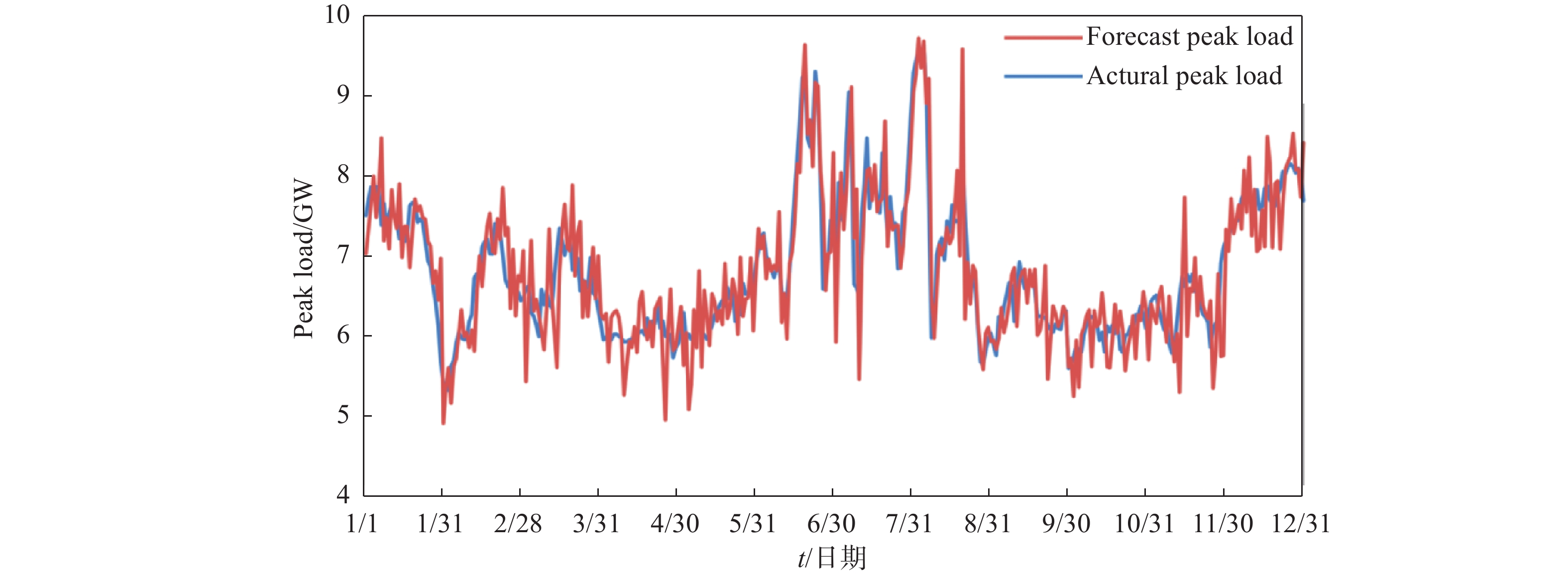
在日常气象服务中,可根据气象要素对日用电负荷峰值的相对危险度开展日用电负荷峰值预测,具体方法如前文所述。根据2013年1月1日至2021年12月31日石家庄市日用电负荷峰值与气象条件的关系计算二者之间的相关关系和相对危险度,利用2022年1月1日至2022年12月31期间对应数据进行检验。由图5的预测值与实际负荷值的对比曲线可见,2条曲线高度一致,预测误差分布情况如表3所示,预报误差在±50 MW之间的有101 d,占比为27.7%,90.1%的预报误差位于±200 MW之间。经分析,预测误差较大的样本,偏低的主要集中在春季,这应该与河北当地春季农田灌溉有一定关系。而预测偏高的样本在夏季和冬季都出现过,经翻查历史资料和分析,夏季主要受转折性天气也就是突发强对流天气的预报准确率限制所致,而冬季则一定程度上与空气污染导致的部分限产有关。整体来说,该预报方法可以用于电力气象服务业务。
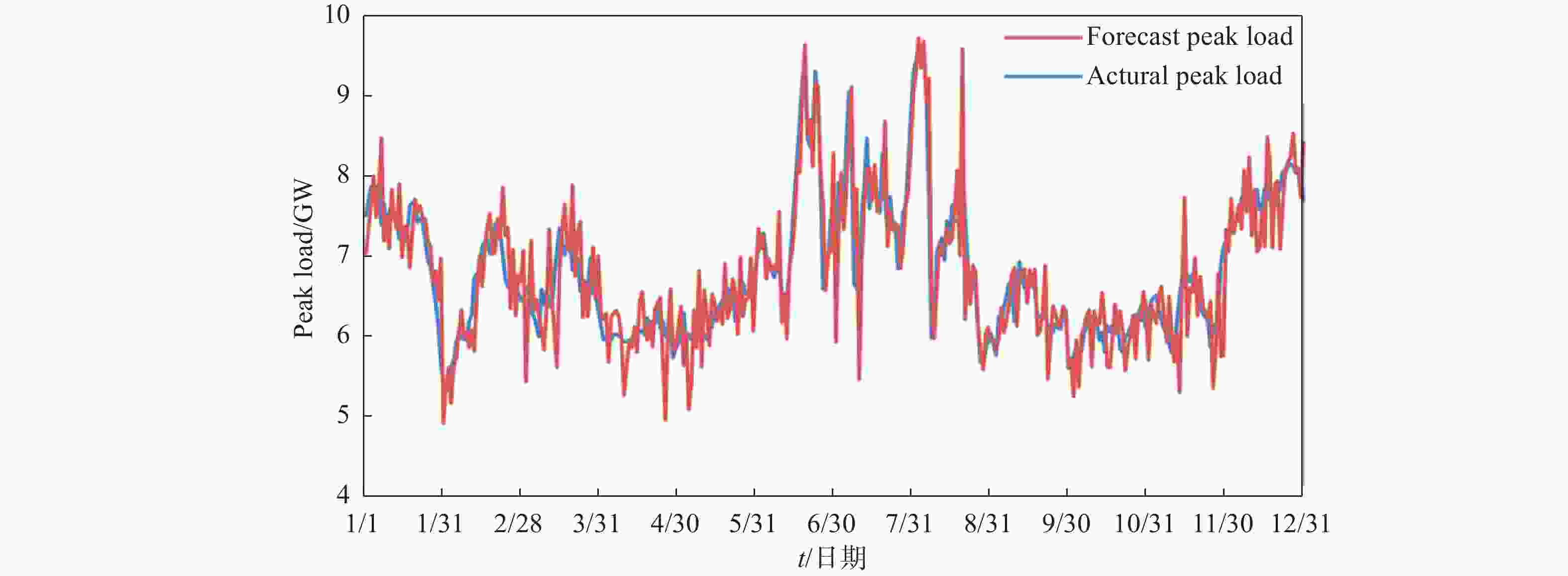
Figure 5. Comparison curve between predicted and actual values of daily peak electricity load in Shijiazhuang in 2022
误差E范围/MW 样本数/个 占比/% −50≤E≤50 101 27.7 −100≤E≤100 186 50.9 −200≤E≤200 329 90.1 E<−200,E>200 36 9.9 Table 3. Prediction error of peak electricity load
-
1)过去10 a,石家庄地区日用电负荷峰值上升趋势较明显,2022年较2013年总体增长近25%。各年度的负荷分布均呈“双峰双谷”型,高峰出现在夏季6~8月,次高峰出现在冬季采暖期11月~次年1月。逐日分布也出现2个峰值,分别出现在上午11时和18时。
2)分析次日用电负荷峰值较当日用电负荷峰值变幅发现,较大变幅的情况多数出现在夏季,且增幅较大的个例多对应高温天气;降幅较大的个例多对应降雨天气。说明气象条件对用电负荷影响显著。
3)利用Spearman秩相关方法筛选出对日用电负荷峰值影响显著的气象要素,利用平滑曲线拟合法绘制气象要素对次日用电负荷峰值的响应曲线并获取到气象要素的响应阈值,根据阈值区间,分段计算气象要素对次日用电负荷峰值的相对危险度,得到不同气象要素发生单位变化引发的用电负荷峰值变化量。并基于此探讨了一种次日用电负荷峰值的预测方法,经检验发现可用于日常电力气象服务业务。
4)本文尝试将气象要素对用电负荷峰值的相对危险度引入用电负荷预测模型,取得了一定的效果。但是文章所研究的区域具有一定局限性,将来将尝试应用本方法开展区域级用电负荷预测,以期为河北用电负荷预测业务提供有力支撑。
Application of Relative Risk of Meteorological Factors in Power Grid Electricity Load Forecasting
doi: 10.16516/j.ceec.2024.1.17
- Received Date: 2023-10-08
- Rev Recd Date: 2023-11-14
- Available Online: 2024-01-30
- Publish Date: 2024-01-10
-
Key words:
- load forecasting /
- Spearman′s rank correlation /
- relative risk /
- quantitative analysis /
- predictive test
Abstract:
| Citation: | QU Xiaoli, YOU Qi, LI Wenqing, et al. Application of relative risk of meteorological factors in power grid electricity load forecasting [J]. Southern energy construction, 2024, 11(1): 166-175 doi: 10.16516/j.ceec.2024.1.17 |







 DownLoad:
DownLoad: