-
随着我国风电事业不断发展，我国海上风电场单机容量从3 MW增长到10 MW，建设场址从沿岸浅海走向深远海[1]。近海的风力发电机基础一般为固定式结构和重力式基础。但是在深远海不易安装，浮式基础在解决深海区风机安装问题上起着重要作用[2]。而浮式风机拖航运输的安全问题亟待解决，本文研究一种新型全潜式浮式风机的拖航稳性，为解决浮式风机拖航运输提供一些参考。
对全潜式浮式风机拖航研究可以参考筒型基础或其他气浮结构的拖航研究以及国内外学者提出的新型浮式结构的理论分析和模型试验。Dymarski等[3]进行了浮式风机在65 m以上水域拖航过程中的稳定性分析，通过模型试验的CFD方法才能获得风机拖航过程中行为的可靠预测。Han等[4]提出了一种水深70~150 m的半潜式水下张力腿平台STLP，研究了其在二阶波浪荷载、风荷载和不同水深的影响下的动力响应。张浦阳等[5]建立海上气浮筒型基础结构拖航模型，对气浮基础进行浮态、稳性、频域和时域分析。韩彦青等[6-7]使用多体动力学方法，建立全潜式浮式风机拖航系统的整体模型，研究了拖航过程中风、浪、流等环境影响因素对风机拖航运动稳定性的影响。丁红岩等[8]采用FAST软件研究全潜式浮式风机在海洋环境下的自振频率及其在不同风环境下的动力响应，得到了全潜式浮式基础的动力特性。倪道俊等[9]通过一步式运输安装船运输现场实验，对复合筒型基础在施工过程中的稳定性。任灏等[10]使用数值模拟软件Moses探究三筒导管架基础湿拖方式以及研究其自浮湿拖浮运特性。
以往的研究中有对浮式基础的拖航进行动力响应分析、稳性分析以及频域和时域分析等，也有对其他结构型式的整机拖航进行稳性分析和动力响应分析。本文所采用的全潜式浮式风机整机重心高，属于高耸的结构物，其浮式基础是基于3种传统结构提出的新型结构型式，相较于一般海洋结构拖航其拖航安全性将面临更多挑战。由于风机结构高耸，拖航过程中受风荷载影响较大，通过研究风荷载对全潜式浮式风机拖航响应及结构动力特性的影响，进一步探讨风速和风向对结构物拖航运动的影响水平。通过NPD风谱，生成时程风速序列[11]，研究不同风速和风浪方向条件下全潜式浮式风机拖航运动特性，以保证漂浮式风机拖航运输的安全，为实际工程提供理论依据。
-
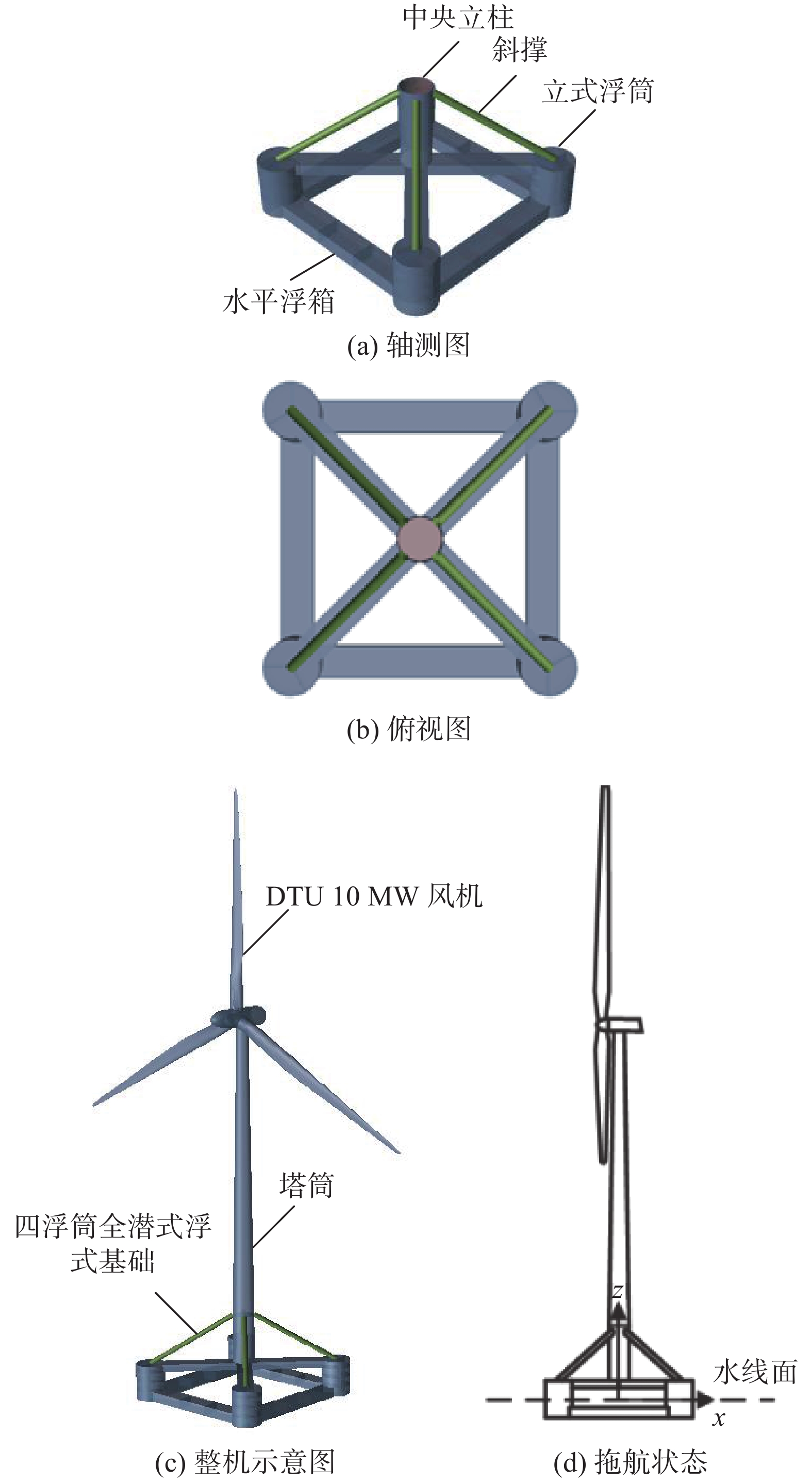
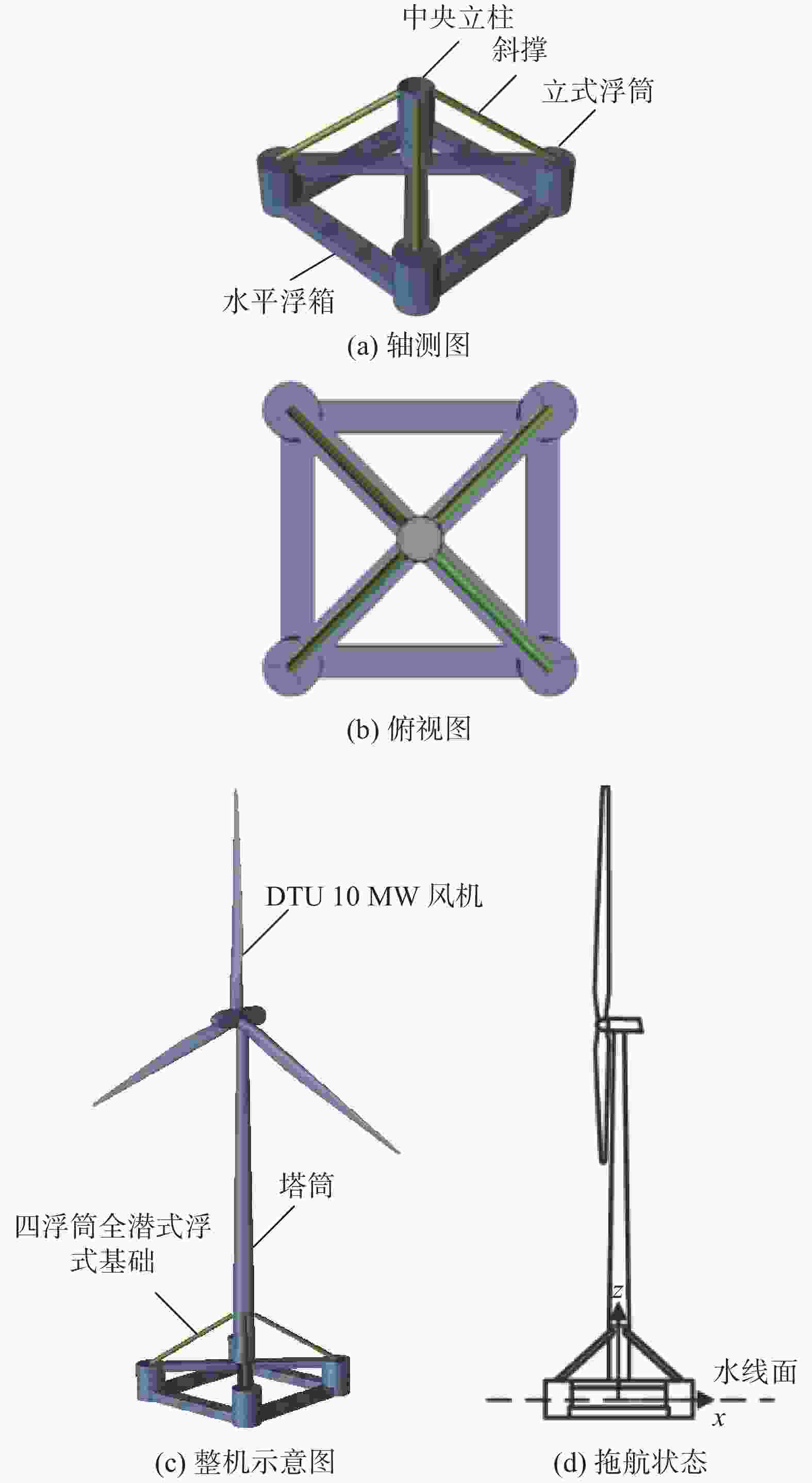
全潜式浮式风机是丁红岩等综合3种传统的结构型式单立柱（Spar-buoy）式、张力腿式（Tension-leg platform）和半潜式（Semi-submersible platform）基础的优点提出一种新型浮式风机[12]，适合超过60 m的深海区域。全潜式浮式风机的拖航系统由基础、风机、拖船和缆绳组成。全潜式基础由立柱、水平浮箱、浮筒、斜撑和水平浮箱组成，基础结构如图1所示，尺寸如表1和表2所示。
Figure 1. Structure diagram of fully submersible floating OWT
参数 值 参数 值 浮筒直径/m 11 水平浮箱高度/m 4 浮筒高度/m 15 水平浮箱宽度/m 6.5 浮筒中轴线间距/m 50 水平撑杆高度/m 3 立柱高度/m 22 排水体积/m3 12 811 立柱直径/m 8.3 基础质量/t 4 812 撑杆直径/m 2 Table 1. Parameters of submersible floating OWT
参数 值 叶轮直径/m 178.3 叶片长度/m 86.366 轮毂高度/m 119 叶轮质量/t 227.962 机舱质量/t 446.036 塔筒质量/t 628.442 Table 2. Parameters of DTU 10 MW OWT
-
本文采用Moses（Mulyi-operational Structural Engineering Simulator）软件[5]进行数值模拟计算，是一种将建模与结构应力分析整合到一起的编程软件。其主要功能包括海上安装模拟、水动力分析、稳性校核、结构分析校核等多个方面。计算时Moses可以实现模拟环境荷载并进行应力分析。
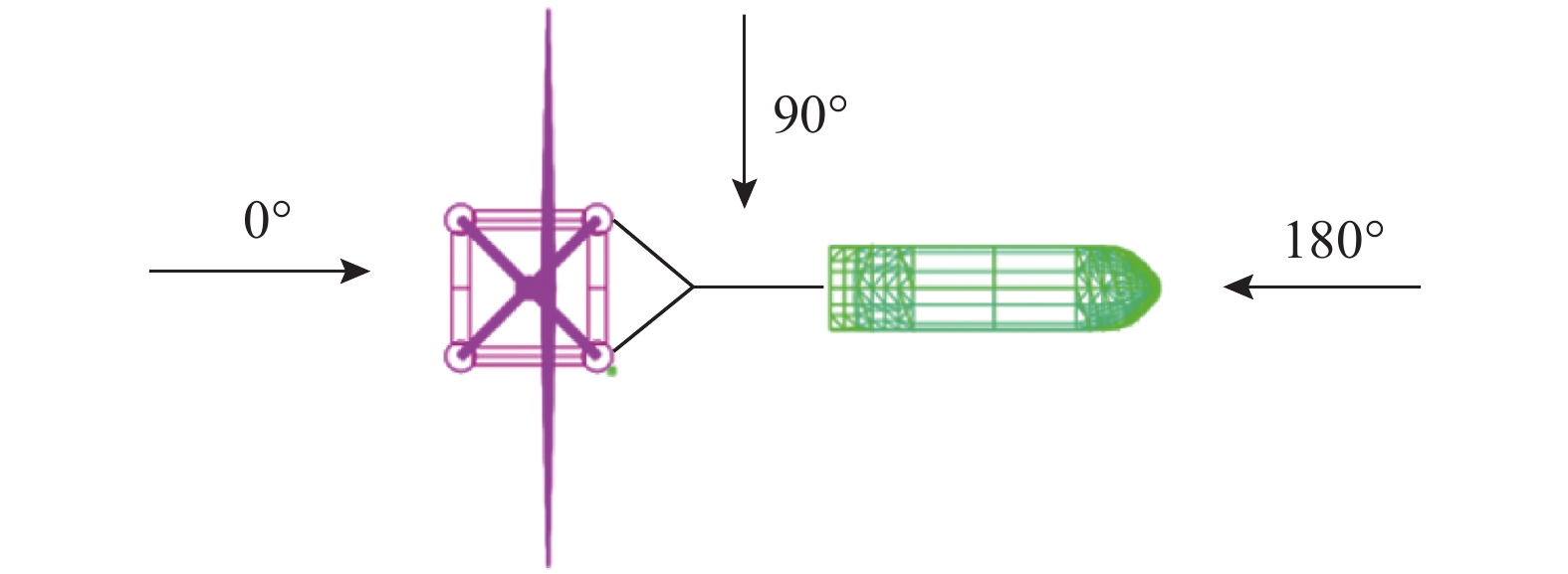
在Moses中建立的模型拖船——全潜式浮式风机拖航系统如图2所示，由拖船-龙须缆-风机组成，其中风机的主要结构可划分为全潜式浮式基础、塔筒和机头。风机和拖船通过Y形的龙须缆相连，龙须缆一端系在拖船尾部，另外两端分别与全潜式浮式风机前端立柱相连。风机整体吃水为5.15 m，基础底座提供的浮力可以承担起整个风机结构的重量。以塔筒底面的几何形心为原点，x轴为垂直正对风机叶片方向，z轴为垂直海面向上，y轴按右手定则确定，则上部风机的重心为（−0.3，0.0，85.5），考虑全潜式基础后，以基础底面的几何形心为原点，重心位置为（−0.3，0，32）。
Figure 2. Towing model diagram of submersible floating OWT
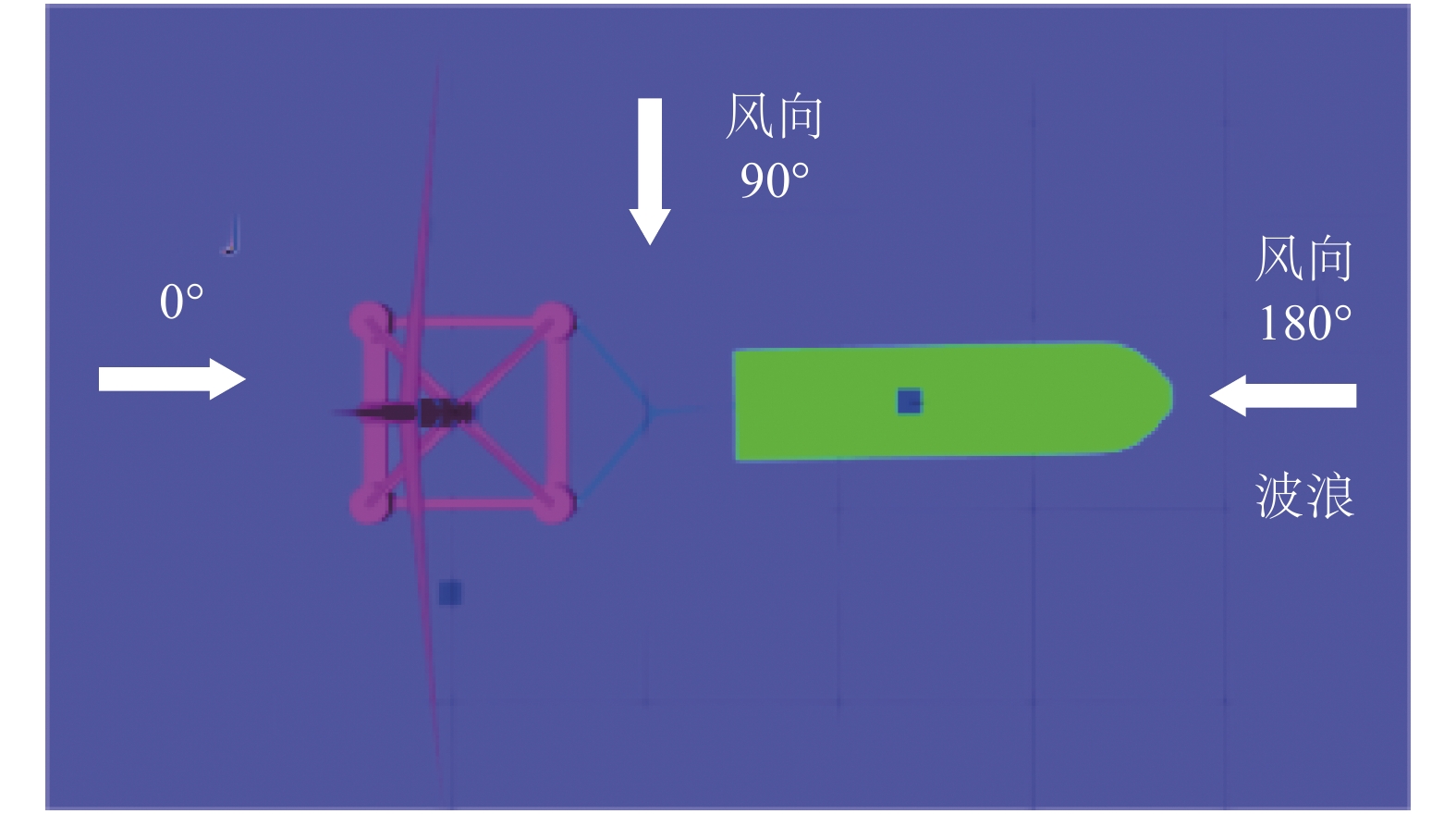
本文主要研究海洋中风荷载对全潜式浮式风机拖航运动稳定性的影响。采用NPD风谱生成时程风速序列进行模拟，张延涛等[13]对渤海风速进行采集与分析，得到某天渤海10 min内平均风速分布在0~18.5 m/s。为研究风速对全潜式浮式风机拖航运动响应的影响，得到不同风速下较为明显的运动响应差别，同时考虑到特殊天气的影响，这里选取渤海某天10 min内的，水面以上0~15.3 m高度范围内的平均风速，即10.3 m/s、20.6 m/s和30.9 m/s 3种不同高度下的风速进行模拟。选取5组不同工况开展全潜式浮式风机的拖航仿真，如表3所示。全潜式浮式风机的基础为漂浮式基础，而漂浮式风机多适用于水深超过50 m的深海区域[14]，本文为研究风速和风向对全潜式浮式风机在深海拖航时的影响，在数值模拟过程中采用控制变量的方法，研究不同风速下全潜式浮式风机的运动响应，以实际情况为基础设置环境条件，拖航水深为100 m。由于实际工程中全部拖航过程可持续24 h以上，数值模拟全过程成本较大，同时一定环境条件下全潜式浮式风机的拖航运动响应时程曲线具有周期性变化规律，因此选择拖航从静止到开始运动的初始阶段中，稳定的1 000 s观察风速和风向对拖航影响程度。以全潜式浮式风机基础底面中点为原点，拖缆点高度同吃水高度为5.2 m。其中工况H1、H2、H3为一组研究不同风速对全潜式浮式风机拖航运动稳性的影响，工况H2、H4、H5为一组研究不同风向对风机拖航运动稳性的影响。
工况 风速/(m·s−2) 有义波高/m 波浪周期/s 风向/(°) H1 10.3 1 8 180 H2 20.6 1 8 180 H3 30.9 1 8 180 H4 20.6 1 8 90 H5 20.6 1 8 0 Table 3. Towing condition settings
-
风是一种不确定的自然环境条件，风压[15]和风力可用规定时段内的平均风速来计算。风荷载[16]的基本表达式为：
风压：
$$ q = \dfrac{1}{2}{\rho _{\mathrm{a}}}U_{T,Z}^2 $$ (1) 式中：
q ——基本风压（Pa）；
ρa ——空气密度（kg/m3）；
UT,Z ——T平均时间内的高度Z处对应的平均风速（m/s）。
和一般建筑结构荷载计算不同，此处基本风压指的是T平均时间内高度Z处的风压大小。
风力：
$$ {F_{\mathrm{W}}} = q\displaystyle \sum\limits_1^n {{C_{{Z}}}} {C_{\mathrm{S}}}{A_n} $$ (2) 式中：
CZ——受风结构高度系数；
CS——构件形状系数；
An ——受风部件的迎风面积（m2）。
由于全潜式浮式风机是高耸结构，风速随着高度的变化而变化，为准确计算风力，不同的高度需要采用不同的高度系数，规范API RP 2SK[17]给出的基于1 min平均风速的风力高度系数转换关系如表4所示，Moses中可以根据需要设置不同规范中的风荷载定义方式进行计算，本文选择国际上广泛认可的API规范作为依据进行计算。
水面以上面积中心高度h/m CZ 0＜h≤15.3 1.00 15.3＜h≤30.5 1.18 30.5＜h≤46.0 1.31 46.0＜h≤61.0 1.40 61.0＜h≤76.0 1.47 Table 4. Height coefficient CZ
由阵风引起的脉动风荷载也同样需要引起注意，当风场的主要能量周期和拖航系统的震荡周期相近时，脉动风可能对拖航系统产生较大的震荡[17]，甚至有可能会引起风和结构物的共振。由此引入了风谱的概念。根据API RP 2A[18]推荐，本文使用NPD谱进行计算：
海平面以上z米处的1 h平均风速Uz为：
$$ {{{U}}_{{z}}}= {{{U}}_{10}}\left[ {1 + {C{\mathrm{ln}}} \left( {\dfrac{{{z}}}{{10}}} \right)} \right] $$ (3) $$ {{C}} = 0.057\;3\sqrt {1 + 0.15{{{U}}_{10}}} $$ (4) 式中：
Uz ——海平面以上z米的1 h平均风速（m/s）；
U10 ——海平面以上10 m处的1 h平均风速（m/s）。
NPD谱表述了风中某一质点纵向风速能量密度波动：
$$ {S_{{\rm{NP}}{{\rm{D}}_f}}}= \dfrac{{320{{\left( {\dfrac{{{{{U}}_{0}}}}{{10}}} \right)}^2}{{\left( {\dfrac{{{z}}}{{10}}} \right)}^{0.45}}}}{{{{\left( {1 + {{{f}}^{0.468}}} \right)}^{3.561}}}} $$ (5) 式中：
${S_{{\rm{NP}}{{\rm{D}}_f}}} $ ——频率f的能量谱密度（m2/s）；
f ——频率（Hz）。
-
浮体在海洋中受力情况复杂，受到惯性力、附加力、回复力和环境荷载等的共同影响，国内外一般基于势流理论解决此类问题[19]。时域势流理论可以通过建立时域控制方程的方法计算浮体在任意波浪击力下的运动响应。目前常采用间接时域法，引入脉冲频谱来建立浮体时域运动方程[20]：
$$ (M + m)\ddot {X_t} + \int\limits_{ - \infty }^t {K_{t - \tau }\dot {X_\tau }{d_\tau }} + {K_{\mathrm{C}}}{X_t} = F $$ (6) 式中：
M ——浮体质量矩阵；
m ——附加质量矩阵；
Xt ——浮体运动位移；
KC——回复力矩阵；
Kt ——时延函数；
F ——波浪力。
Moses中根据纽马克β假设对式进行计算，式（6）可简化为：
$$ M\ddot X + B\dot X + KX = F $$ (7) 根据拉格朗日中值定理及纽马克假设，t时刻的速度可以表示为：
$$ {\dot X_{t + 1}} = {\dot X_i} + (1 - \delta ){\ddot X_t}\Delta t + \delta {\ddot X_{i + 1}}\Delta t $$ (8) 将一段时间内的时间段按照一定步长进行离散，根据拉格朗日中值定理并进行泰勒级数展开，得：
$$ {X_{t + 1}} = {X_t} + \dot X\Delta t + \left[ {\left( {\dfrac{1}{2} - \beta } \right){{\ddot X}_i} + \beta {{\ddot X}_{t + 1}}} \right]\Delta {t^2} $$ (9) 式中，$ \delta $和β是和精度、稳定性有关的参数，Moses中默认$ \delta $=0.5，保证积分过程中振幅保持不变，取β=0.25为平均加速度法。经计算，可以得到全潜式浮式风机在模拟工况中的运动响应时程曲线。
-
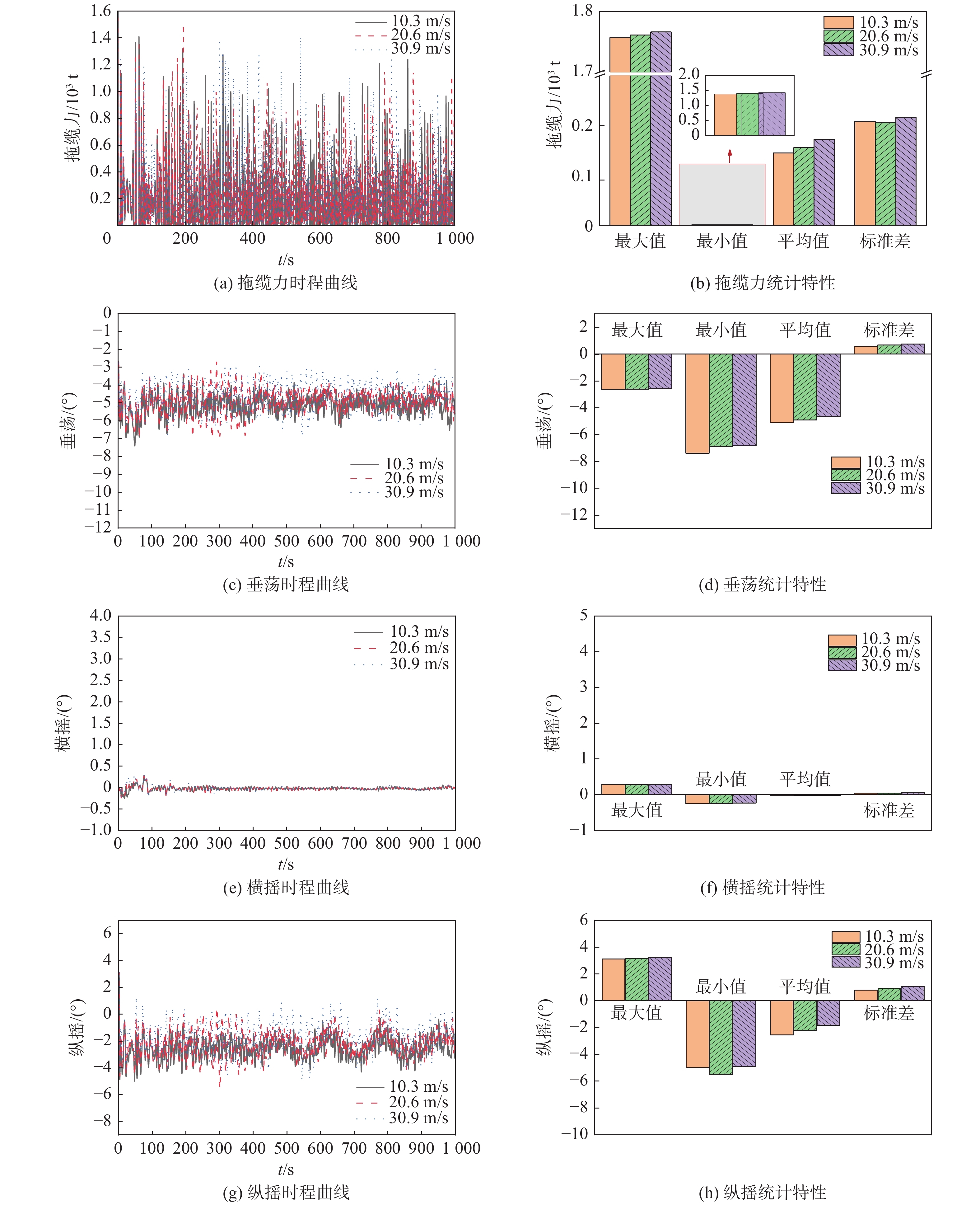
在波高为1 m，波浪周期为8 s，风浪方向为顺浪180°，航速为4.5 kn时，分别对风速为10.3 m/s、20.6 m/s、30.9 m/s时的拖航过程进行模拟，得到风机拖缆力、垂荡、横摇和纵摇随时间的变化曲线和运动统计数据，如图3所示。
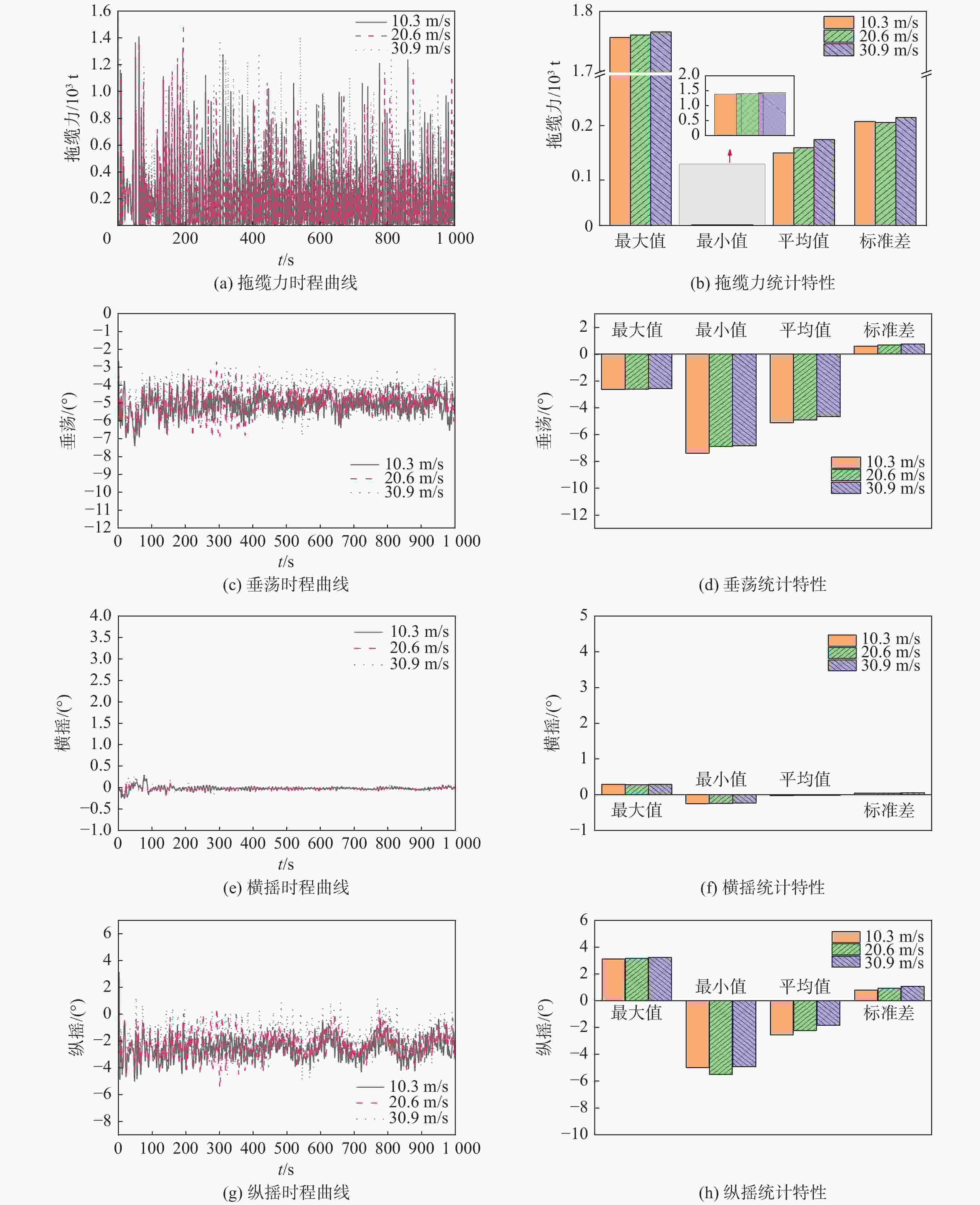
Figure 3. Time history curves and statistical parameters of fully submersible floating OWT at different wind speeds
图3（a）、图3（b）为不同风速下全潜式浮式风机的拖缆力时程曲线和统计特性，由图可知，全潜式浮式风机拖航过程中风机受到的拖缆力在一定范围内波动，并且随着风速的增加而增加。图3（c）、图3（d）为不同风速下风机的垂荡时程曲线和统计特性，由图可知，在起步时风机会有较明显的垂荡运动，之后的拖航过程中垂荡会在一定范围内波动。随着风速的增加震荡幅度也会增大，风速为30.9 m/s时风机垂荡的波动范围为±1.5°，风速为20.6 m/s时风机垂荡的幅动范围为±0.5 m。图3（e）、图3（f）为不同风速下风机的横摇时程曲线和统计特性，由图可知，在浪向180°的条件下，起步150 s时间内风机的横摇角相对较大，这是因为在惯性力和初始力瞬变的作用下，拖缆力和运动响应远大于稳定运动时情况的阶段，实际情况中不会出现上述情况，可以将其视为异常值进行清洗，之后会逐渐稳定在±0.1°范围内波动，因此风速的改变对风机拖航过程中的横摇角没有太大的影响。图3（g）、图3（h）为不同风速下风机的纵摇时程曲线和统计特性，由图可知，风机在拖航过程中的纵摇角在±3.5°内均匀波动，随着风速的增加风机纵摇角的幅动范围也有所增大。
-
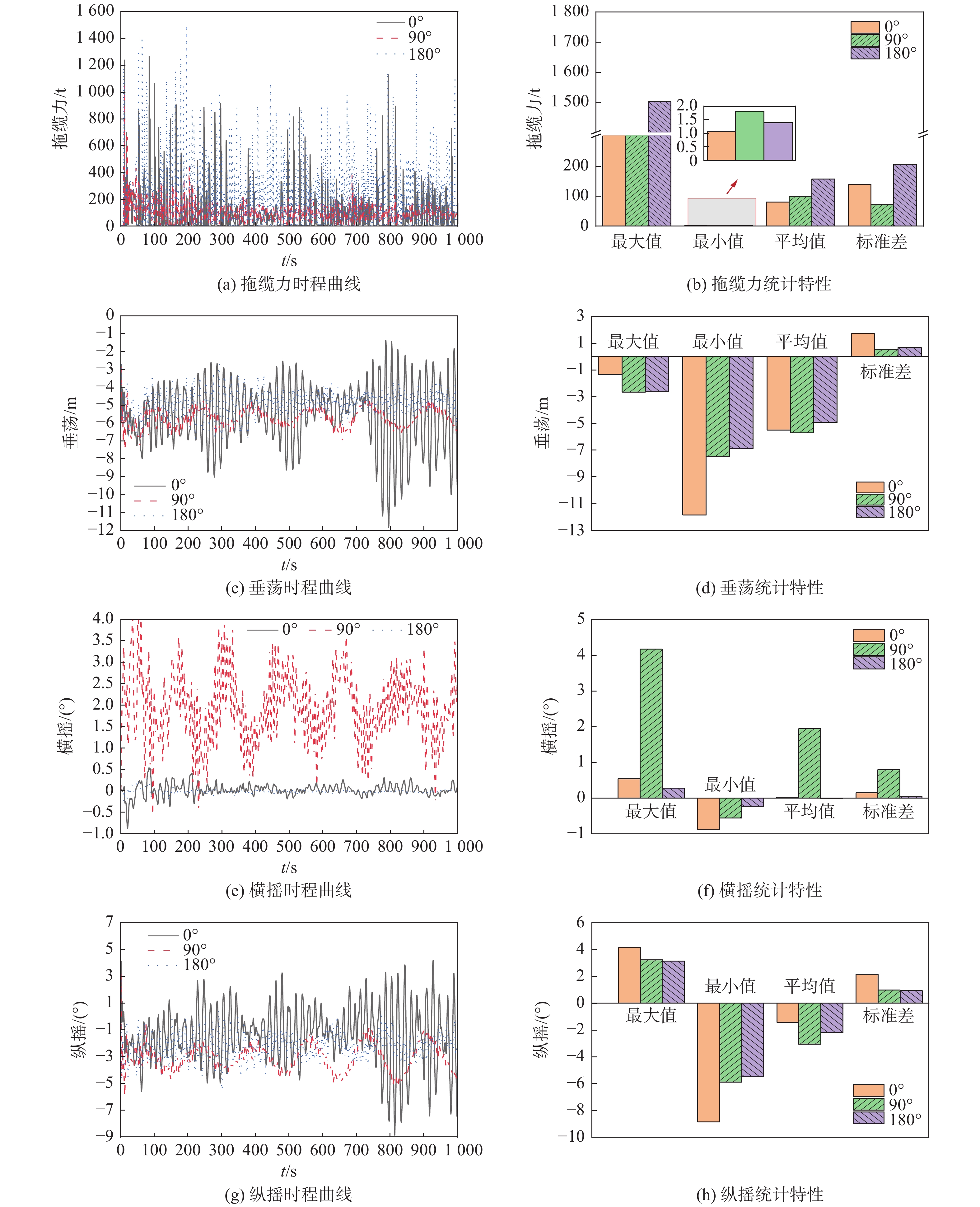
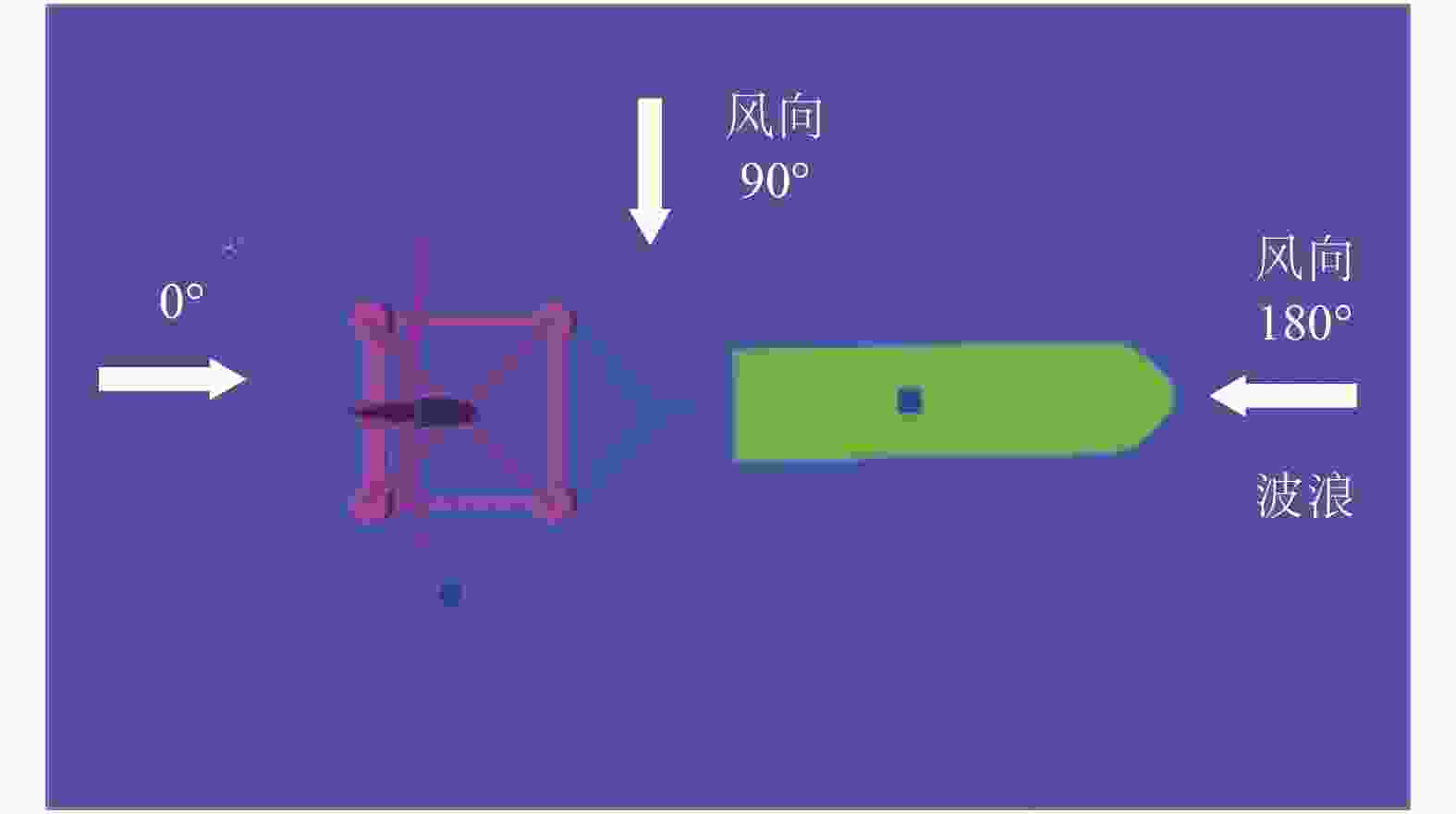
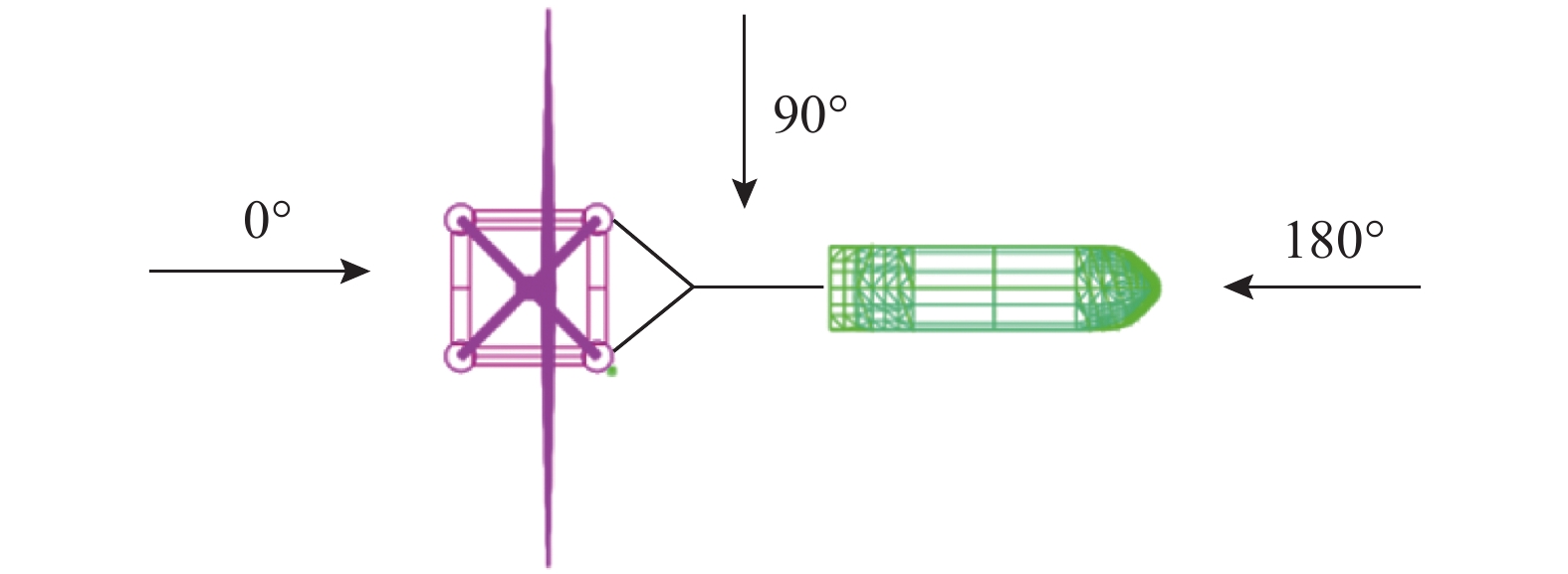
分析风速为40 m/s，波高为1 m，波浪周期为8 s，航速为4.5 kn下，风浪方向对拖航稳性的影响，选取相对于拖航坐标系顺浪0°、横浪90°和逆浪180°的海况进行模拟分析，如图4所示。
Figure 4. Definition of wind and wave direction
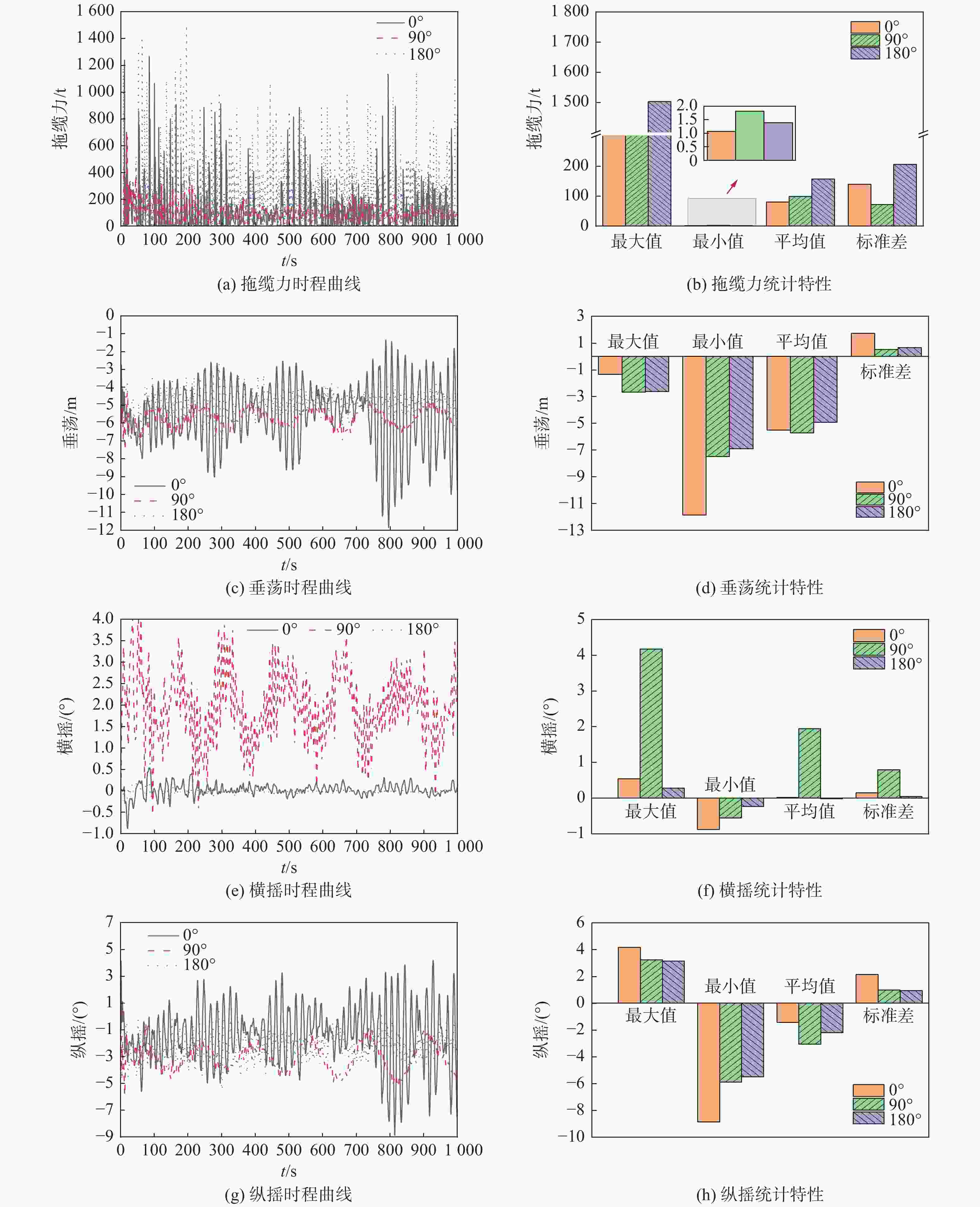
图5为不同风浪方向条件下拖缆力、垂荡、横摇和纵摇的时程曲线和运动统计数据。其中，图5（a）、图5（b）为不同风浪方向条件下全潜式浮式风机受到的拖缆力时程曲线和统计特性，当风浪方向为180°和0°时，拖缆力较大；当风浪方向为90°时，拖缆力较小。图5（c）、图5（d）为不同风浪方向条件下风机的垂荡时程曲线和统计特性，3种不同方向的垂荡运动中，相较于90°和180°浪向而言，0°浪向的垂荡运动幅度更大，且在700 s后，该幅度更为明显，最大达到±5 m。图5（e）、图5（f）为不同风浪方向条件下风机的横摇时程曲线和统计特性，当波浪方向与前进方向平行时，风机的横摇运动幅度较小；当风机受到横浪时，也就是90°时，风浪方向沿垂直风机前进方向入射，引起较大横摇弯矩，因此在此方向上横摇较大。图5（g）、图5（h）为不同风浪方向条件下风机的纵摇时程曲线和统计特性，拖航过程中风机的纵摇角变化趋势和垂荡类似，0°浪向的纵摇运动幅度更大，且在700 s后，该幅度更为明显。这是由于在700 s后，0°波浪条件下，与风机前进方向一致的波浪方向对风机的振动产生了正向激励，导致了风机固有周期的变动。波浪周期与风机固有周期接近，从而引发了风机与波浪之间的共振现象。相比之下，其他方向的波浪对风机固有周期的影响较小，不太可能出现类似的共振情况。
Figure 5. Time-history curves of fully submersible floating OWT at different wind and wave directions
-
相比于横摇运动，全潜式浮式风机的纵摇和垂荡运动受风速影响较为明显，风速越大，运动幅度越大。起步150 s时间内风机的横摇角相对较大，这是因为在惯性力和初始力瞬变的作用下，拖缆力和运动响应远大于稳定运动时情况的阶段，实际情况中不会出现上述情况，可以将其视为异常值进行处理，因此，风速的改变对风机拖航过程中的横摇角没有太大的影响。
0°波浪条件下，全潜式浮式风机的纵摇和垂荡运动较大，风机前进方向与0°波浪方向一致的，对风机的振动产生了正向击力，导致了风机固有周期的改变为与波浪周期固有周期接近，从而引发了共振现象。因此，在实际工程中，为了保证风机的稳定运行和减少振动问题，通常会采取避免顺浪拖航的措施。通过避免顺浪拖航，可以降低风机振动和共振的风险，提高风机的可靠性和运行效率。
-
本研究对全潜式浮式风机在不同工况的运动情况进行数值模拟，选取NPD风谱，研究不同风速和不同风向条件下对全潜式浮式风机拖航运动响应的影响。得出以下结论：
1）全潜式浮式风机在拖航过程中受到的拖缆力受风速和风浪方向产生的影响较明显，风速越大，拖缆力越大，风浪方向平行于拖航方向时，拖缆力较大。
2）全潜式浮式风机的稳性较好，除横浪作用下横摇角略大外，在所选工况中横摇角均小于1°，故风浪方向对全潜式浮式风机的横摇影响最大，这是因为拖航过程中全潜式浮式风机基础的横摇主要由基础与横摇自振频率上的外界荷载共振引起。
3）根据本研究的计算结果，在保证拖航过程在拖航窗口期的前提下，实际工程中全潜式浮式风机拖航建议最大程度地进行逆风拖航，逆风拖航时虽然拖缆力较大，但风机的横摇、纵摇以及垂荡运动响应较为稳定，对于全潜式浮式风机这一高耸结构物来说最为安全。当风向与拖航方向相垂直时，容易引发较大程度的横摇运动，拖航过程较为危险，实际工程中应尽量避免。
4）根据数值模拟结果，当拖航方向与风向相反时，即使是在超过平均海况的较大风速30.9 m/s下，全潜式浮式风机的运动响应及拖缆力仍能满足安全拖航的要求，说明全潜式浮式风机的稳定性较好，当实际工程中出现了因风荷载导致风机拖缆力、垂荡、横摇和纵摇等指标超出正常范围的情况，该风机结构具有一定的抗风险能力，可在辅助运输船的帮助下及时调整拖航方向，保证结构的稳定性。
Effect of Wind Loads on Towing Response of Submersible Floating OWT
doi: 10.16516/j.ceec.2024.1.18
- Received Date: 2023-08-14
- Rev Recd Date: 2023-09-12
- Available Online: 2024-01-30
- Publish Date: 2024-01-10
-
Key words:
- fully submersible floating OWT /
- towing stability /
- Moses numerical simulation /
- wind speed /
- wind direction
Abstract:
| Citation: | ZHAO Yebin, REN Jianyu, LE Conghuan. Effect of wind loads on towing response of submersible floating OWT [J]. Southern energy construction, 2024, 11(1): 176-184 doi: 10.16516/j.ceec.2024.1.18
|
DownLoad:
