Thermodynamic Analysis of Highview Power's Liquid Air Energy Storage Pilot Plant

降低能源供应中的碳含量，探索以可再生能源为主的电力系统已成为全球范围内的发展趋势。可再生能源的供应本质上是间歇性和分布不均的，储能成为不可或缺的支撑技术。压缩空气储能被认为是最具有发展前景的大规模储能技术之一^{[1- 2]}。储气装置是压缩空气储能的关键部件，地下洞穴受到地理环境的限制，而地面储气装置的设备成本较高^[3]。液化空气储能（Liquid Air Energy Storage，LAES）的基本原理是在电量富余时将空气液化储能，在用电高峰时利用液态空气发电释能^[4]。LAES系统的能量密度高于压缩空气，对地理环境的依赖较小，是一种新兴的技术经济可行的大规模储能解决方案^[5]。

LAES系统不仅可以作为独立的储能电站，还能实现可再生能源的空间转移。美国国家可再生能源实验室提出了一种解耦的LAES系统来利用海上可再生能源^[6]。海上可再生能源就地产生液态空气，然后利用液化天然气槽船、罐车将液态空气运输到最终使用地点，最后利用液态空气发电。此外，LAES可以与燃气轮机系统相结合，利用LAES技术提供燃气轮机工作所需的高压空气，同时提高燃气轮机的效能^[7]。

尽管关于LAES的第一篇文献出现在1974年，但该技术在最近几年才得到世界各地众多研究人员的关注，大多数研究工作通过过程建模和能量分析来研究LAES系统的热力学性能，相关模拟研究见表1。主流建模工具有Aspen HYSYS、Aspen Plus和MATLAB。前两者是成熟的过程模拟软件，自带物性库和单元模块，无需编程操作简便；后者是通用的编程环境，需要从REFPROP或者EES等软件调用物性库，可以便捷地使用智能优化算法。研究者们通过模拟不同的液化方式和储热储冷方式，使LAES的循环效率达到60%。近年来利用LNG冷能提升循环效率成为研究热点。由于LNG冷能（110～300 K）覆盖空气液化温区（80～300 K）的较大范围，可以极大减少空气液化耗能，使LAES的循环效率可以突破100%。

目前针对LAES系统级的实验研究还相当缺乏，仅Highview Power LAES中试装置公开了一部分现场试验测试数据^[18]。该中试装置于2010年在英国斯劳（Slough）开始运行，额定规模为350 kW/2.5 MWh，随后被搬迁到伯明翰大学进行进一步的研究和开发，于2015－2018年公开了部分测试数据^{[19- 20]}。文章基于Highview Power LAES中试装置建立热力学建模，采用MATLAB+REFPROP作为建模工具，利用中试装置公开的测试数据验证模型的准确性。在此基础上，分析该中试装置的㶲损失以及关键操作参数对储能过程和释能过程的影响规律，为提高LAES系统的循环效率提供参考依据。

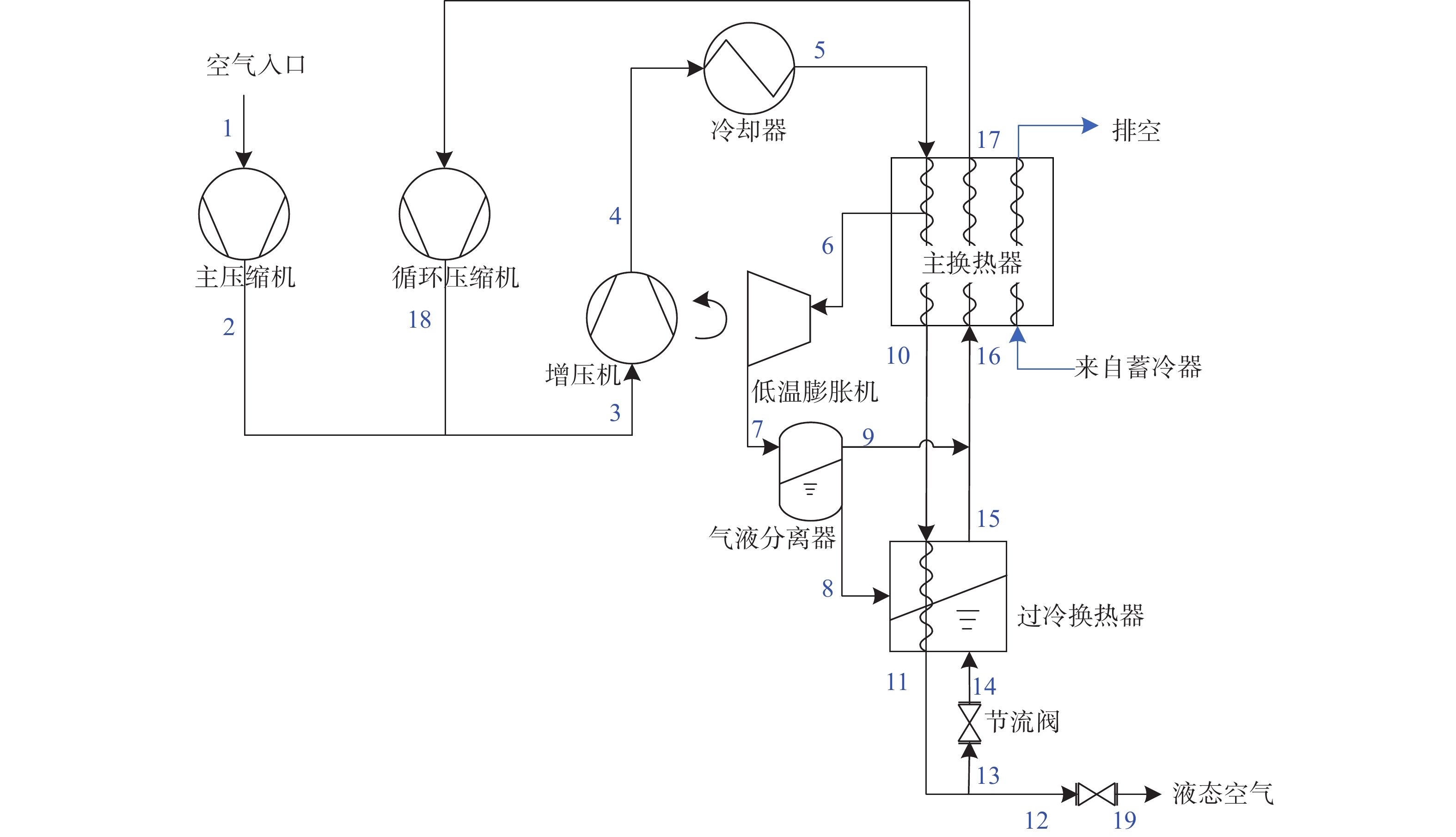
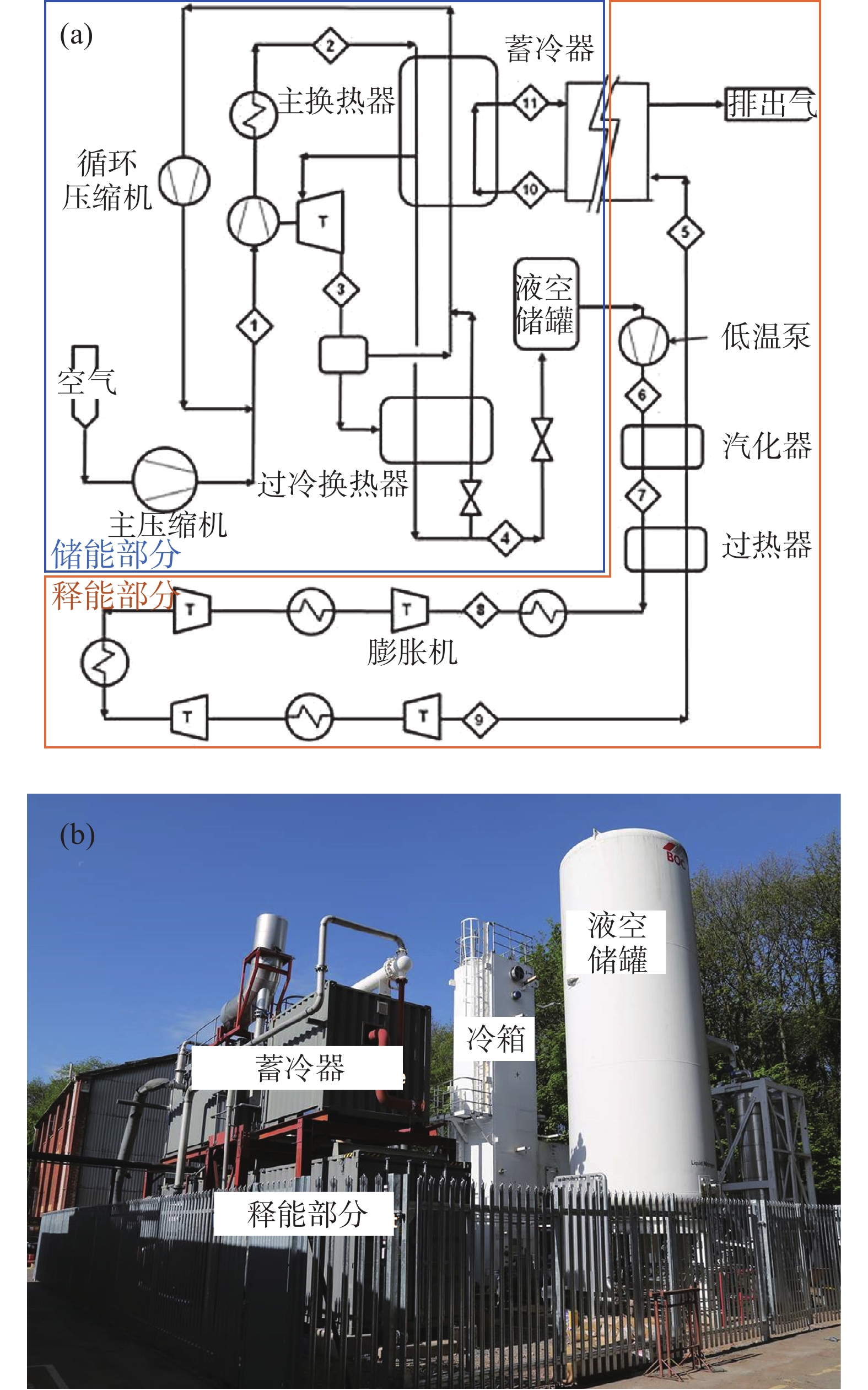
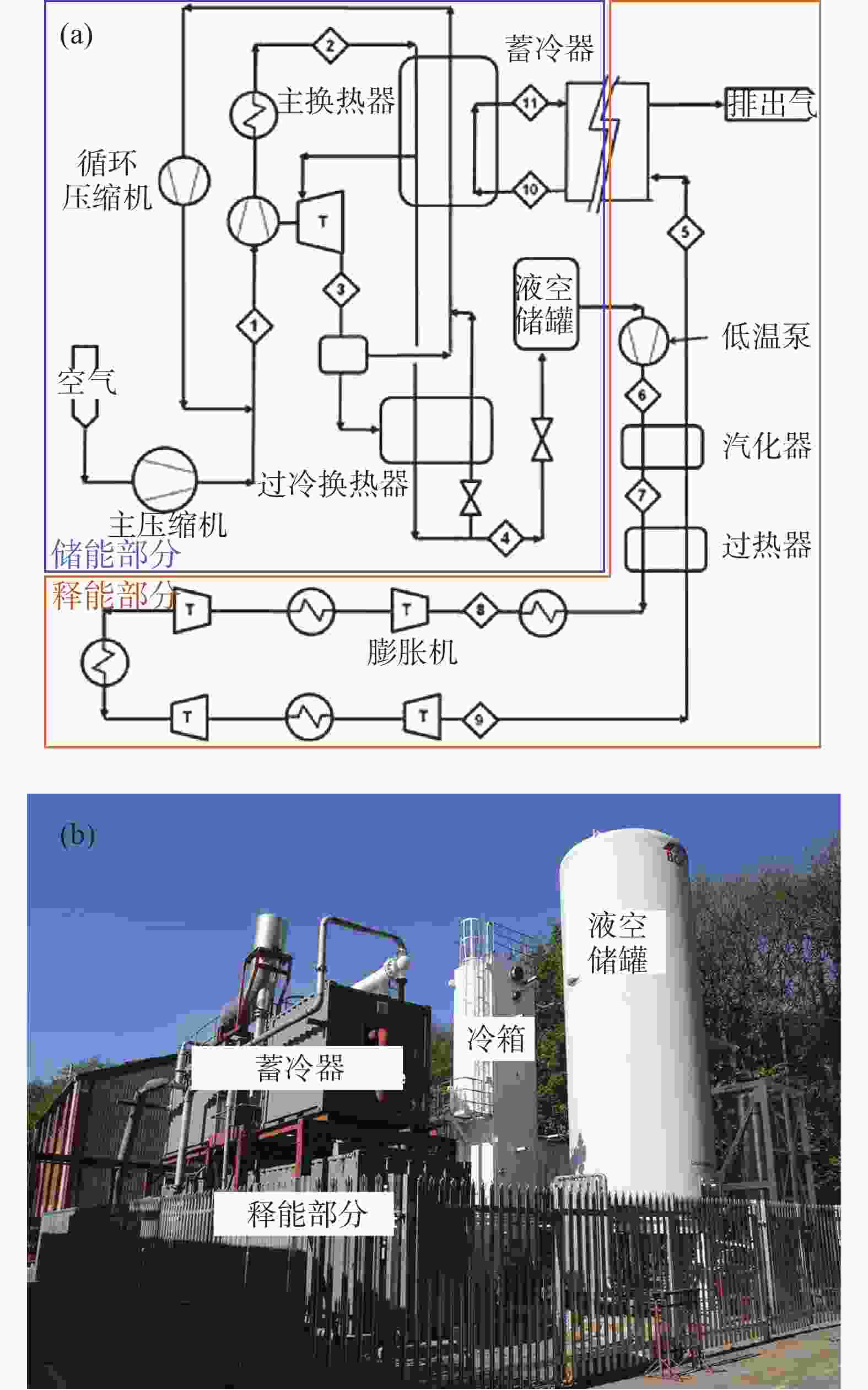
Highview Power LAES中试装置的流程如图1(a)所示，现场设备如图1(b)所示。空气液化部分由成都空分公司提供，采用改进的克劳德循环。循环压缩机和主压缩机均为螺杆式压缩机，由阿特拉斯·科普柯提供，两台压缩机由变速电机驱动，可调节空气质量流量。冷箱低温端设置了一个液体浸没式过冷换热器，旨在降低局部富氧液体蒸发导致的碳氢化合物着火的风险^[19]。蓄冷器由8个石英岩填充床组成，这些填充床可以串联或并联，安装在集装箱内，采用珍珠岩绝热^[9]。冷量通过释能后的干空气从汽化器中回收。释能部分由往复式低温泵、换热器和四级膨胀机组成。低温泵同样由变速电机驱动，可控制释能压力。膨胀机前的加热器为逆流式换热器，由水-乙二醇加热低温空气，热量来自邻近发电站的余热，使各级膨胀机入口温度维持在288～343 K。四级串联的膨胀机由Concepts NREC提供，实现近似等温膨胀。

Figure 1.  Flow chart (a)^[19] and site photo (b)^[11] of LAES pilot plant

在储能高压为12 bar、释能压力为56 bar的操作条件下，释能功率210 kW，储能循环效率仅8%^[19]。效率低的原因有待进一步分析。目前仅公开了中试装置储能过程和释能过程分开测试的数据，且储能过程使用空气、释能过程使用液氮作为工质。因此，文章将分别对储能过程和释能过程进行热力学建模与分析。

Highview Power LAES中试装置的储能过程如图2所示。针对各个部件建立质量平衡与能量平衡方程，根据已知的部分条件求解19个状态点的温度、压力、质量流量等热力学状态。

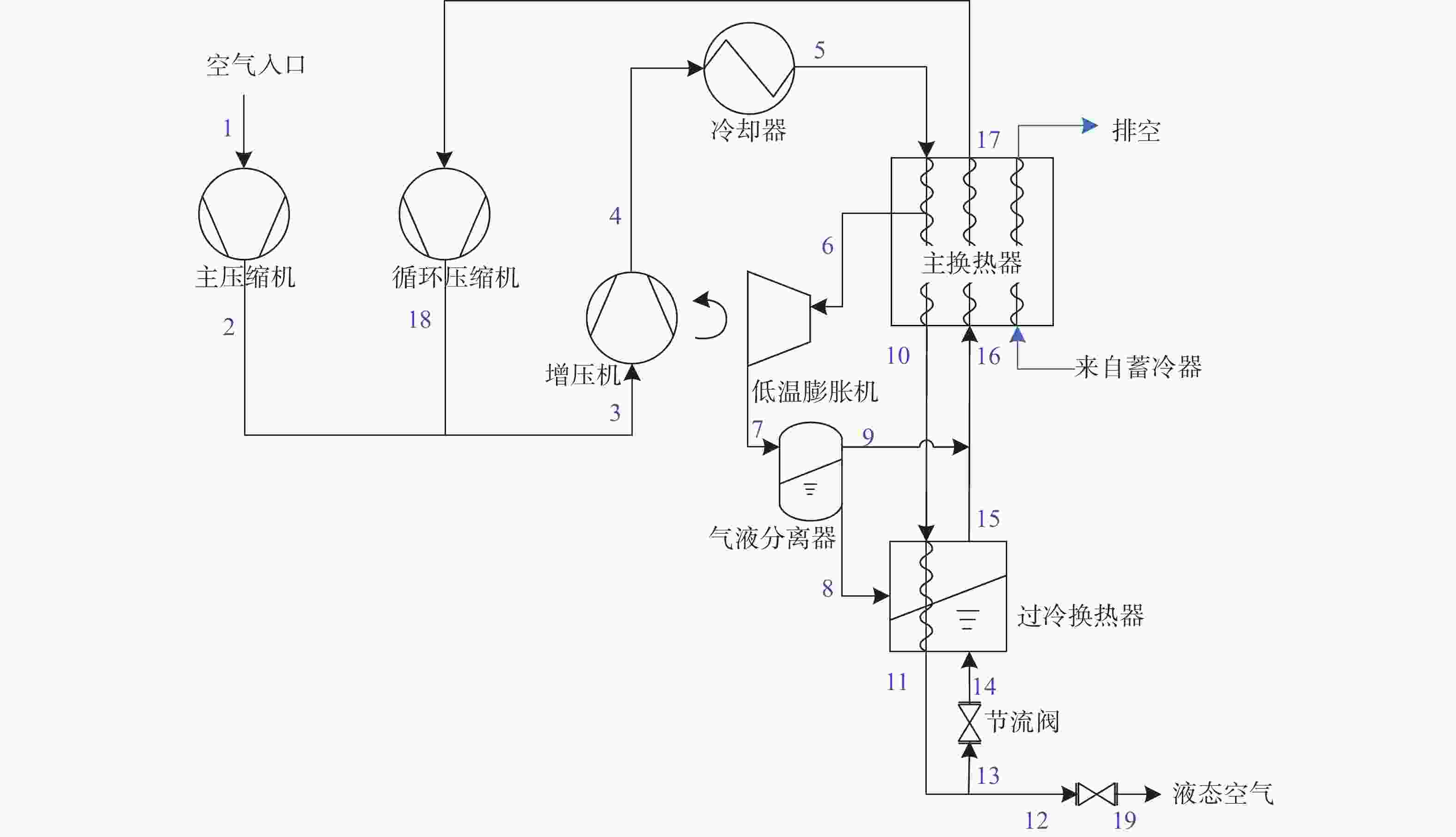
Figure 2.  Flow chart of LAES pilot plant charge process^[20]

进料空气以室温常压状态进入压缩机组，经主压缩机和增压机绝热压缩到指定压力然后冷却至室温；未液化的回流空气经循环压缩机和增压机绝热压缩到指定压力然后冷却至室温。主压缩机的功率和放热量为：

式中：

W_c,m ——主压缩机功率（kW）；

m_m ——主压缩机质量流量（kg/s）；

h ——空气比焓（kJ/kg）；

η_c ——压缩机等熵效率；

Q_c,m ——主压缩机放热量（kW）。

下标s表示等熵过程，2'表示压缩终了状态。循环压缩机的功率W_c,r和放热量Q_c,r计算方法与主压缩机相同，两台压缩机的功率之和为压缩机组总功率。

增压机由低温膨胀机驱动，压缩终了压力p₄由低温膨胀机的输出功率确定，反过来p₄又决定了低温膨胀机的入口压力p₆，即低温膨胀机的做功能力。计算过程中，4点的热力学状态需要迭代求解，使低温膨胀机的传动功率等于增压机的耗功，即同时满足下列两个式子：

式中：

W_c,b ——增压机功率（kW）；

m_b ——增压机质量流量（kg/s）；

W_e ——低温膨胀机输出功率（kW）；

η_e,b ——低温膨胀机驱动增压机的传动效率；

η_b ——增压机等熵效率。

低温膨胀机输出功率为：

式中：

m_e ——低温膨胀机质量流量（kg/s）；

η_e ——膨胀机等熵效率。

低温膨胀机的制冷量与输出功率相等，即Q_e=W_e。

压缩后的空气经冷却器降温至室温：

式中：

Q_c,b ——冷却器放热量（kW）。

低温膨胀机出口空气被少量液化，进入气液分离器，分离后的气体进入主换热器为其提供冷量，液体进入过冷换热器为其提供冷量，状态点7的干度x₇决定了气体和液体的质量。

主换热器为三股流体的逆流式换热器。热流体为压缩后的空气，从室温被冷却至100 K左右，一股冷流体为未液化空气，另一股冷流体来自蓄冷换热器。主换热器能量守恒和质量守恒分别为：

式中：

Q_cs ——蓄冷器带走的热量（kW）。

过冷换热器为两股流体的逆流式换热器，其中热流体为压缩后经主换热器冷却后的空气，冷流体来自节流阀和气液分离器。过冷换热器能量守恒和质量守恒分别为：

空气经主换热器和过冷换热器预冷到转化温度以下，此时焦耳-汤姆逊系数为正，节流后空气压力和温度均降低，空气被部分液化。节流为等焓过程：

根据19点的比焓和压力可以确定该点的干度x₁₉，即确定了液态空气量m_liq和液化率y：

式中：

m_liq ——液体质量流量（kg/s）；

y ——液化率。

液化耗能为每千克液态空气消耗的电能，即

式中：

w_liq ——液化能耗（kJ/kg）。

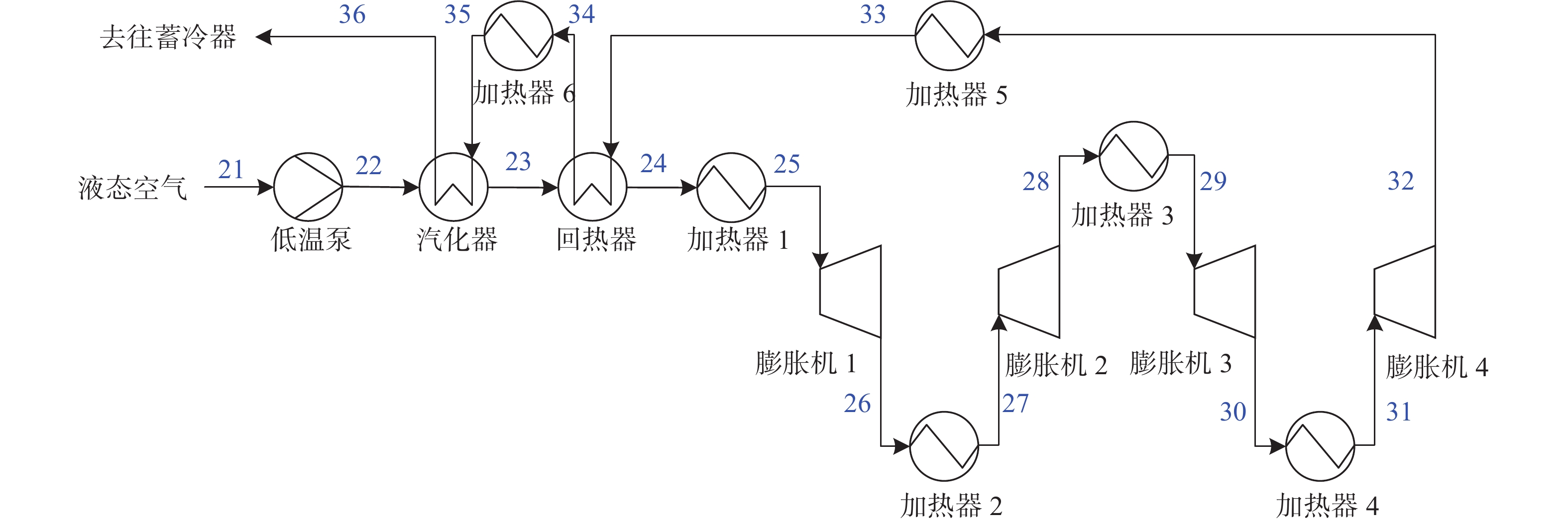
释能过程如图3所示。针对各个部件建立质量平衡与能量平衡方程，求解16个状态点的温度、压力、质量流量等热力学状态。

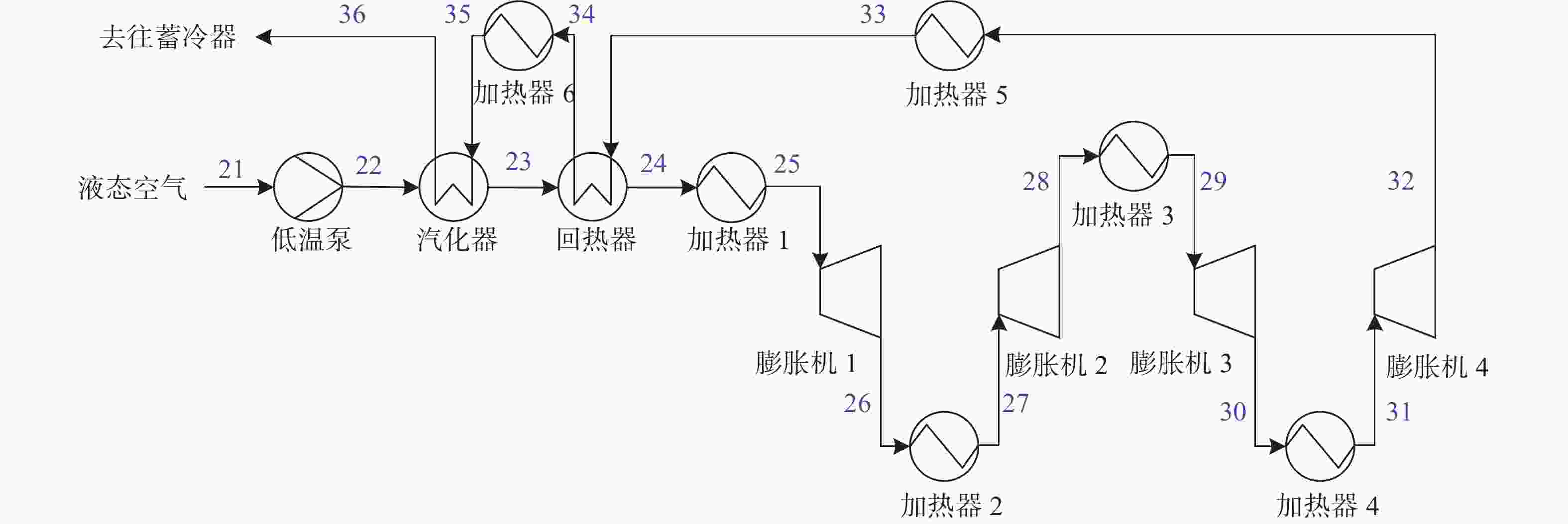
Figure 3.  Flow chart of LAES pilot plant discharge process^[20]

释能过程中，液体经低温泵加压至释能压力，低温泵消耗的能量和功率分别为：

式中：

w_p ——低温泵能耗（kJ/kg）；

p ——压力（kPa）；

η_p ——低温泵等熵效率；

ρ_l ——液体密度（kg/m³）；

W_p ——低温泵功率（kW）；

m_dis ——释能过程液体质量流量（kg/s）。

汽化器和回热器都是逆流式换热器。换热器的热力学状态受到能量平衡和夹点温差的限制，以汽化器为例，其能量平衡方程为：

液空复温后以高温高压气体状态进入膨胀机组，经绝热膨胀带动发电机完成释能。膨胀机组总输出功率为4台膨胀机输出功率之和，每级膨胀机做功：

式中：

w_t ——膨胀机输出比功（kJ/kg）；

W_t ——膨胀机输出功率（kW）；

η_t ——膨胀机等熵效率。

系统的循环效率定义为单位质量液体在释能阶段输出能量与储能阶段消耗的能量之比，代表着系统的综合储能效率。

式中：

η_cyc ——循环电电效率。

将热力学模型在MATLAB环境中进行编程求解，储能过程工质为空气，释能过程工质为液氮，采用以下假设条件：（1）空气为氮气、氧气、氩气的混合物，物理性质从REFPROP软件调用；（2）管道无压降，主换热器中存在0.2 bar压降，汽化器中存在3.5%压降；（3）不存在漏热；（4）气液分离器视为理想分离器，不考虑气液夹带。

根据文献[20]公开的中试装置实测参数设定模型的入口空气参数、高压压力、节流后压力、释能压力等部分参数，根据热力学模型计算其余状态点的热力学参数。储能过程各状态点的计算结果与测量结果列于表2，释能过程计算结果列于表3。计算结果与测量结果比较接近，表明热力学模型能较好地反映中试装置的运行情况。

表2和表3对应的储能、释能过程中各主要设备的能耗与做功功率计算结果列于表4。储能过程液化率仅0.17，液化能耗0.69 kWh/kg，而克劳德循环的液化率通常在0.6以上，液化能耗约0.3 kWh/kg^[21]。释能过程低温泵耗功10.87 kW，四级膨胀机共输出248.75 kW，单位质量液氮做功0.041 kWh/kg。若忽略储能和释能过程工质的差异，则循环效率η_cyc=0.041/0.69×100%=6%。文献报道该中试装置的循环效率为5%～8%^[19]。这么低的循环效率使该中试装置的实用性很低，有必要对循环的㶲损失及关键参数的影响进行分析，寻求提升循环效率的方法。

根据热力学第二定律，能量并不总是全部转换为功。其中可转换为功的能量被称为㶲，能量中㶲的比例越大表示其品味越高。㶲在不可逆过程中会损耗。㶲分析通过揭示各个过程存在的㶲损，反映各环节能量转换与传递的完善程度，其中㶲损最大的环节是最需要优化的。机械能和电能原则上可以全部转化为功，因此全为㶲。流动的流体所具有的㶲称为焓㶲，可表示为：

式中：

E_i ——第i个状态点的焓㶲（kW）；

T_a ——环境温度（K）；

s_i ——第i个状态点的比熵[kJ/(kg·K)]；

s_a ——环境状态比熵[kJ/(kg·K)]。

文章中环境状态的温度和压力分别为300 K和1 bar。

热量不能全部转化为功，其具有的㶲可表示为：

式中：

E_h,j ——第j个加热器的热量㶲（kW）；

${\bar T_{{\text{h}},j}}$ ——第j个加热器的平均温度（K）；

Q_h,j ——第j个加热器的热量（kW）。

各个设备的㶲平衡方程为：

式中：

ΔE ——㶲损（kW）。

下标in表示输入，out表示输出。输入或输出的㶲包括机械能、电能、焓㶲和热量㶲。

分别计算各个设备的㶲损，所有设备的㶲损之和为该过程的总㶲损。㶲效率定义为系统有效利用的㶲和外界输入系统的㶲的比值。储能过程和释能过程的㶲效率表达式如下：

式中：

η_E ——㶲效率。

表2和表3对应的储能、释能过程中主要设备的㶲损如图4所示。

Figure 4.  Exergy loss

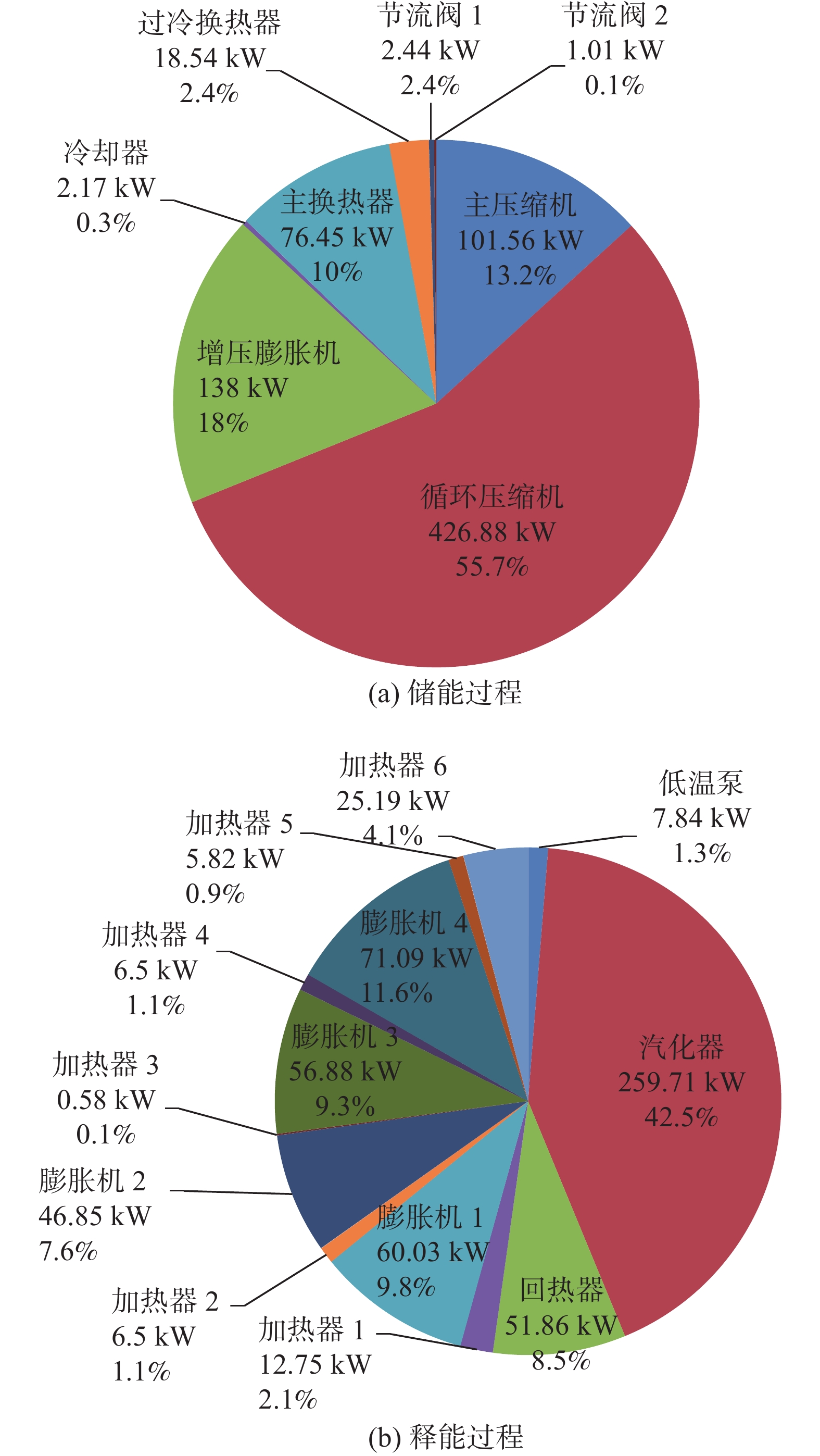
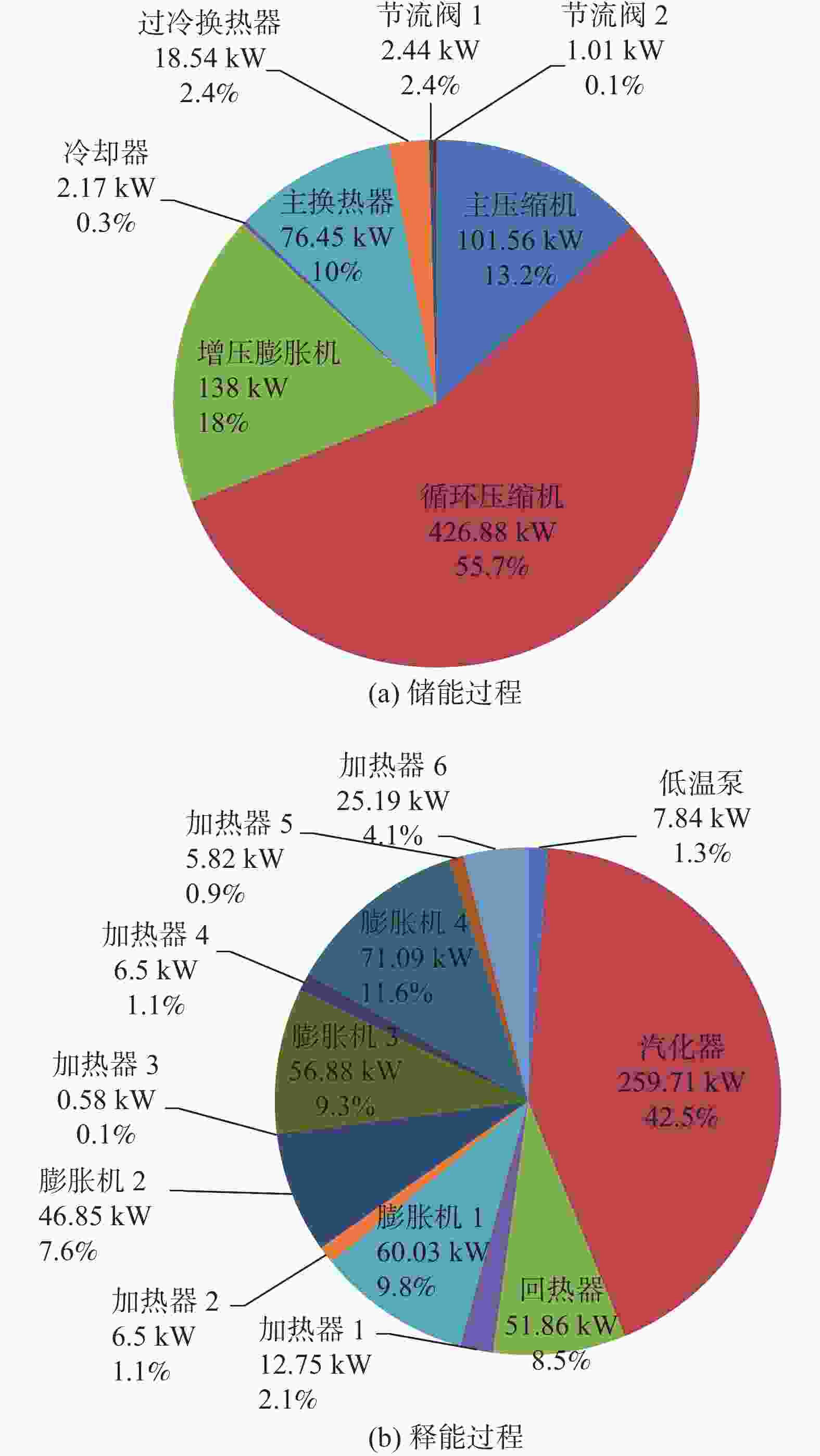
储能过程的总㶲损为767 kW，外界输入储能过程的㶲为1029 kW，可得储能过程㶲效率为25.5%。如图4(a)所示，㶲损最大的设备是循环压缩机，占总㶲损的比例达55.7%。一方面是因为78%的空气由循环压缩机增压，而且787.68 kW的压缩热未被回收利用；另一方面循环压缩机的等熵效率仅63%，不可逆损失较大。降低储能过程㶲损可以从回收压缩热^[22]、提升压缩机等熵效率着手。此外，可以尝试将合适的冷源引入系统，用来降低压缩机进口空气温度，减少压缩机的功耗^[17]。

释能过程的总㶲损为611.7 kW，外界输入释能过程的㶲为1.102 MW，释能㶲效率为44.5%。如图4(b)所示，㶲损最大的设备是汽化器，占总㶲损的比例达42%。汽化器中冷热两股流体在汽化器热端（状态点23和35）的温差达到约140 K，如此巨大的换热温差使得该换热器不可逆损失较大。降低释能过程㶲损可以从优化换热物流匹配，减小换热温差入手。

Highview Power LAES中试装置在不改变工艺流程的情况下，影响储能过程效率的独立变量有以下6个：高压压力p₂、节流后压力p₁₉、增压膨胀机分流量m₆、增压膨胀机入口温度T₆、节流分流量m₁₃、蓄冷器回收冷量Q_cs。本节通过控制变量法逐一分析6个关键参数对液化率和液化能耗的影响，6组参数的设置范围见表5。

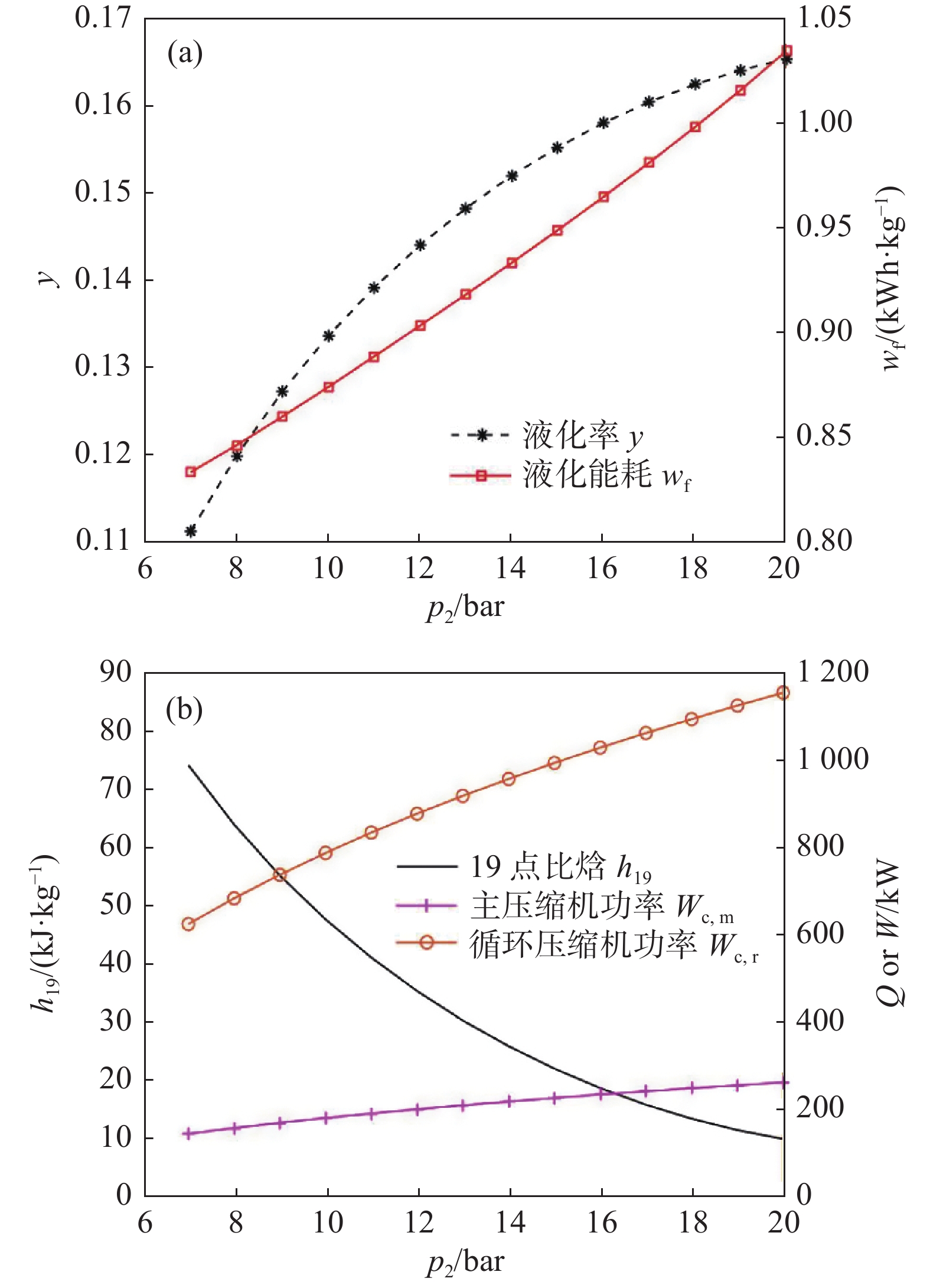
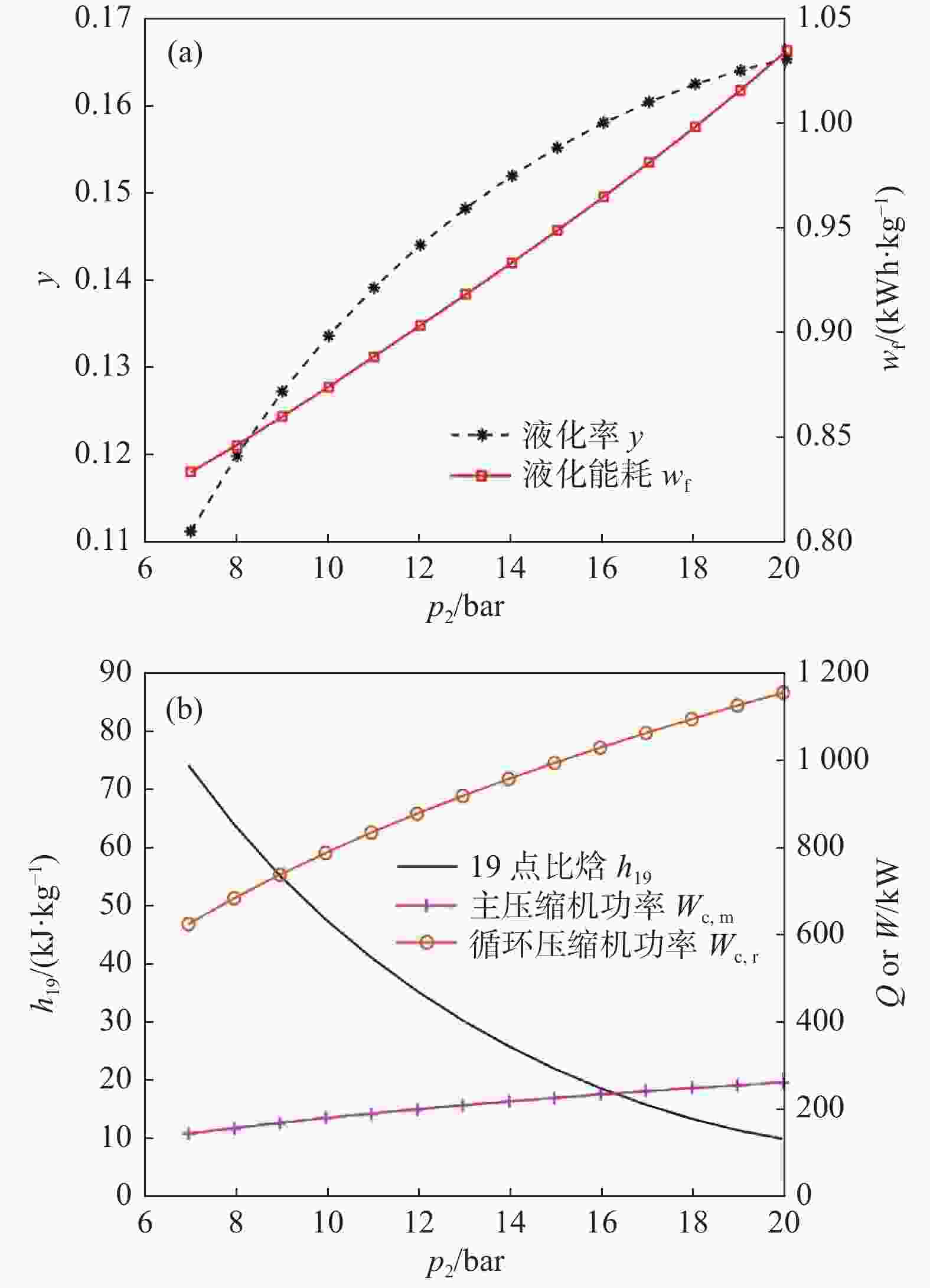
高压压力p₂对液化率和液化能耗的影响规律如图5所示。随着p₂增大，液化率和液化能耗同时增加。当p₂超过13 bar时，液化率增速放缓，而液化能耗几乎线性增加，如图5(a)所示。图5(b)解释了液化率和液化能耗增加的原因。p₂增加意味着压缩后比焓h₂降低，从而使节流后比焓h₁₉显著减低，状态点19为气液两相，其他条件不变时，比焓越低液化率越高。另一方面，p₂增加使主压缩机和循环压缩机功率均增加。p₂从7 bar增加至20 bar，液化率增加48%，压缩机组功率增加了84%，两者综合的结果导致液化能耗增加24%。因此不宜依靠增加p₂来提升液化率，对于此中试装置，10 bar左右是较合适的。

Figure 5.  Effect of compressor high pressure

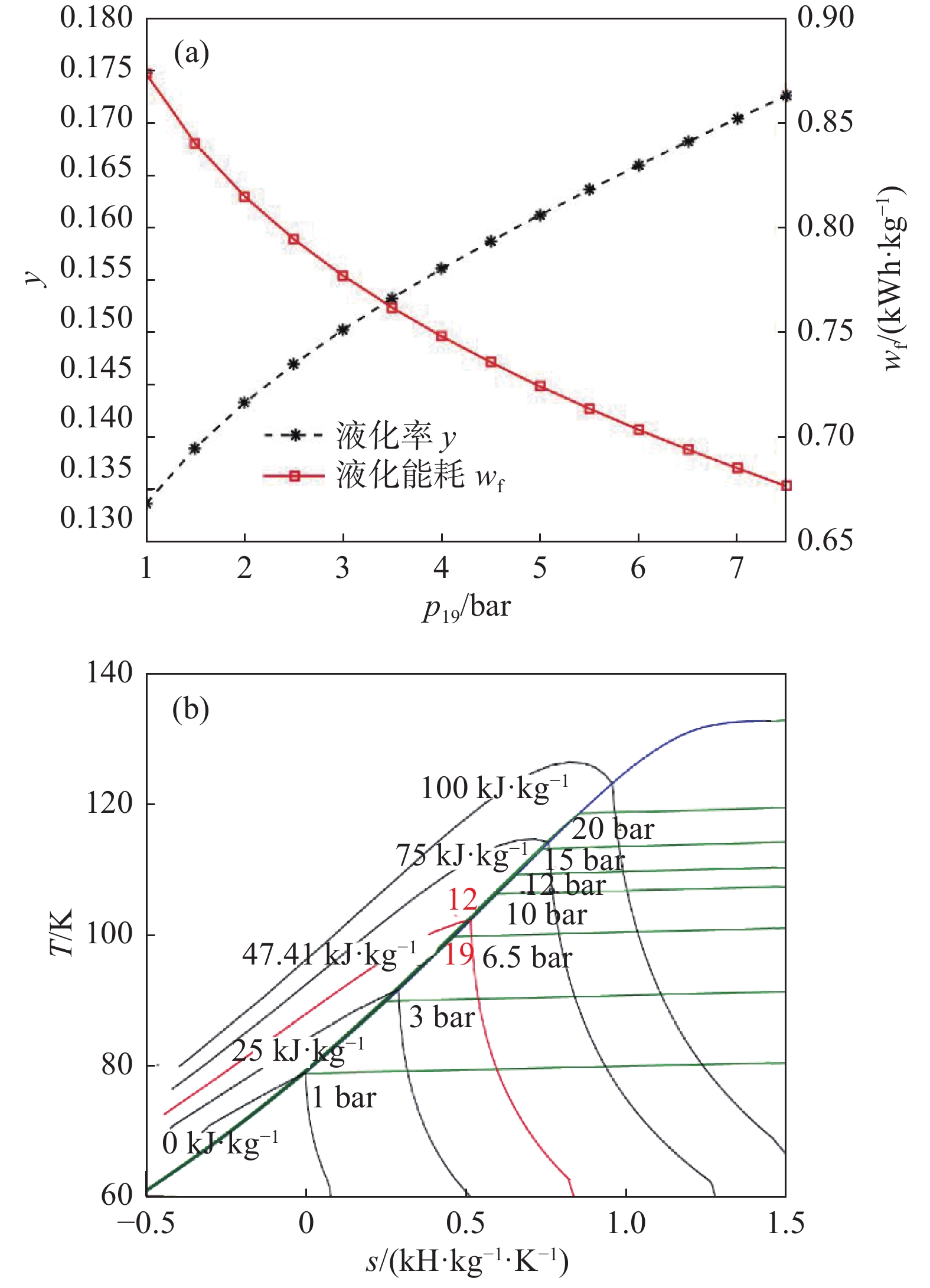
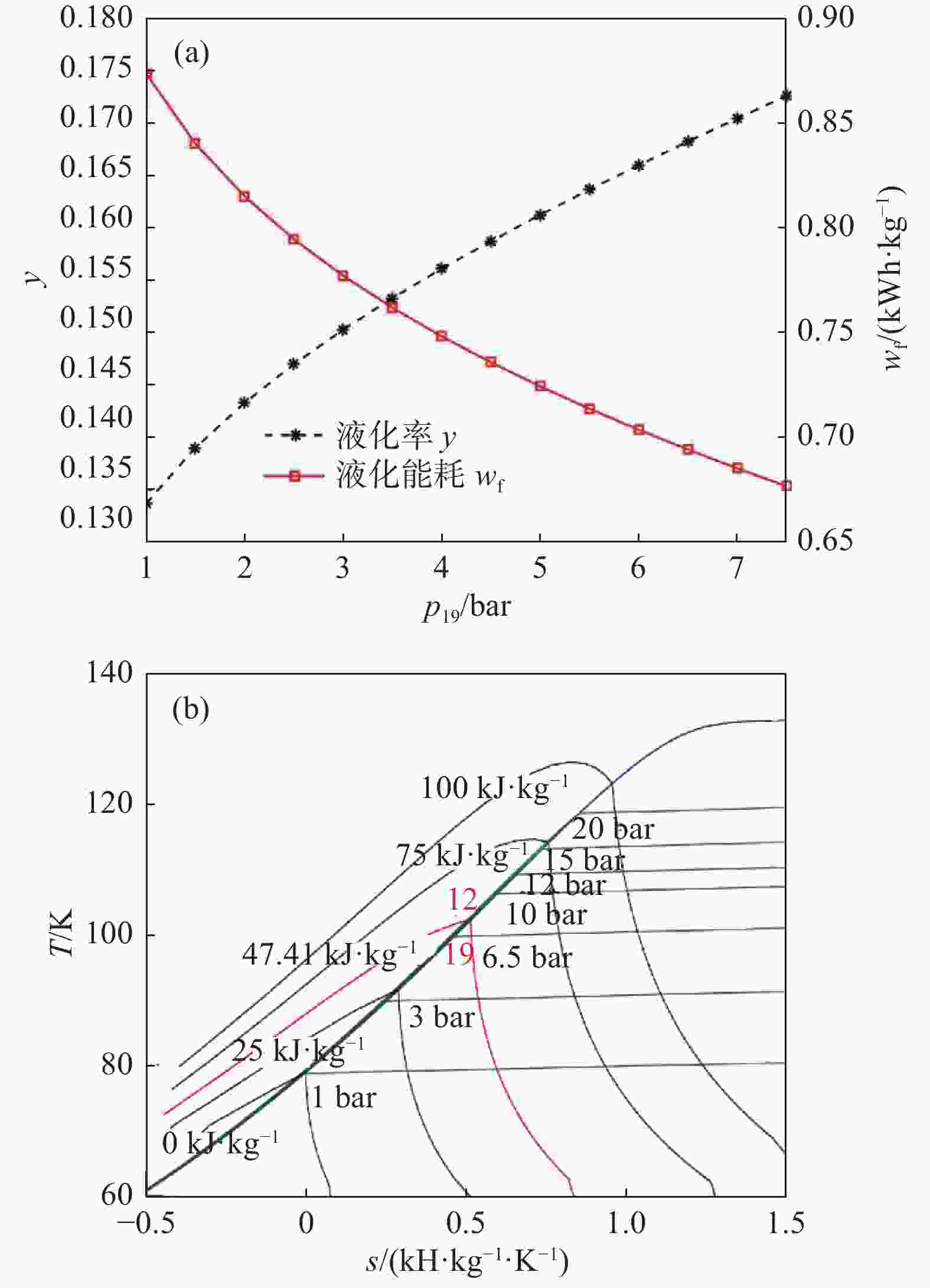
中试装置节流后（状态点19）的气液两相空气全部进入储罐，因此要求19点的干度低于0.1（即液体质量分数高于0.9），否则无法有效利用储罐容积。节流后的干度由压力p₁₉及其比焓h₁₉共同决定。h₁₉主要受高压压力p₂影响，保持其他变量不变，p₁₉对液化率和液化能耗的影响规律如图6所示。随着p₁₉增大，液化率增加、液化能耗降低。这是由空气的等焓线所决定的。图6(b)为空气的温熵图，其中红色等焓线表示节流过程，压力越高，等焓线越靠近左侧饱和液线，即液化率越高。p₁₉增大不影响压缩机组的功率，因此液化能耗随液化率升高而降低。需要注意的是，节流后压力越高越好仅适用于节流后气液两相全部进入储罐这种情况。实际上更为常见的做法是节流至更低压力（如3 bar）气液分离后仅液态空气进入储罐，气态空气返流至换热器提供冷量^[23]。因为较低的液空压力对应着较低的温度，有利于更长时间的存储。

Figure 6.  Effect of the pressure after throttling

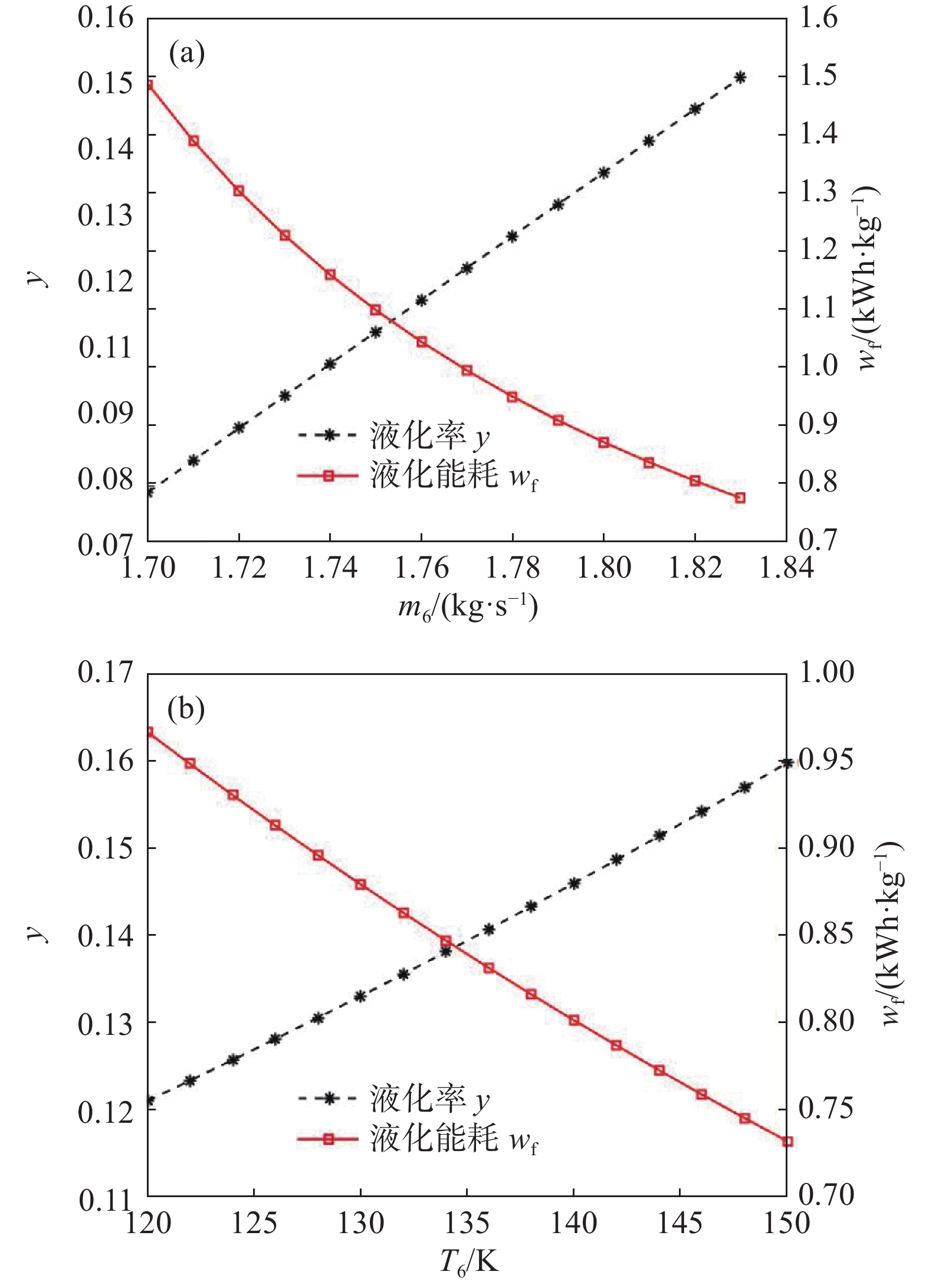
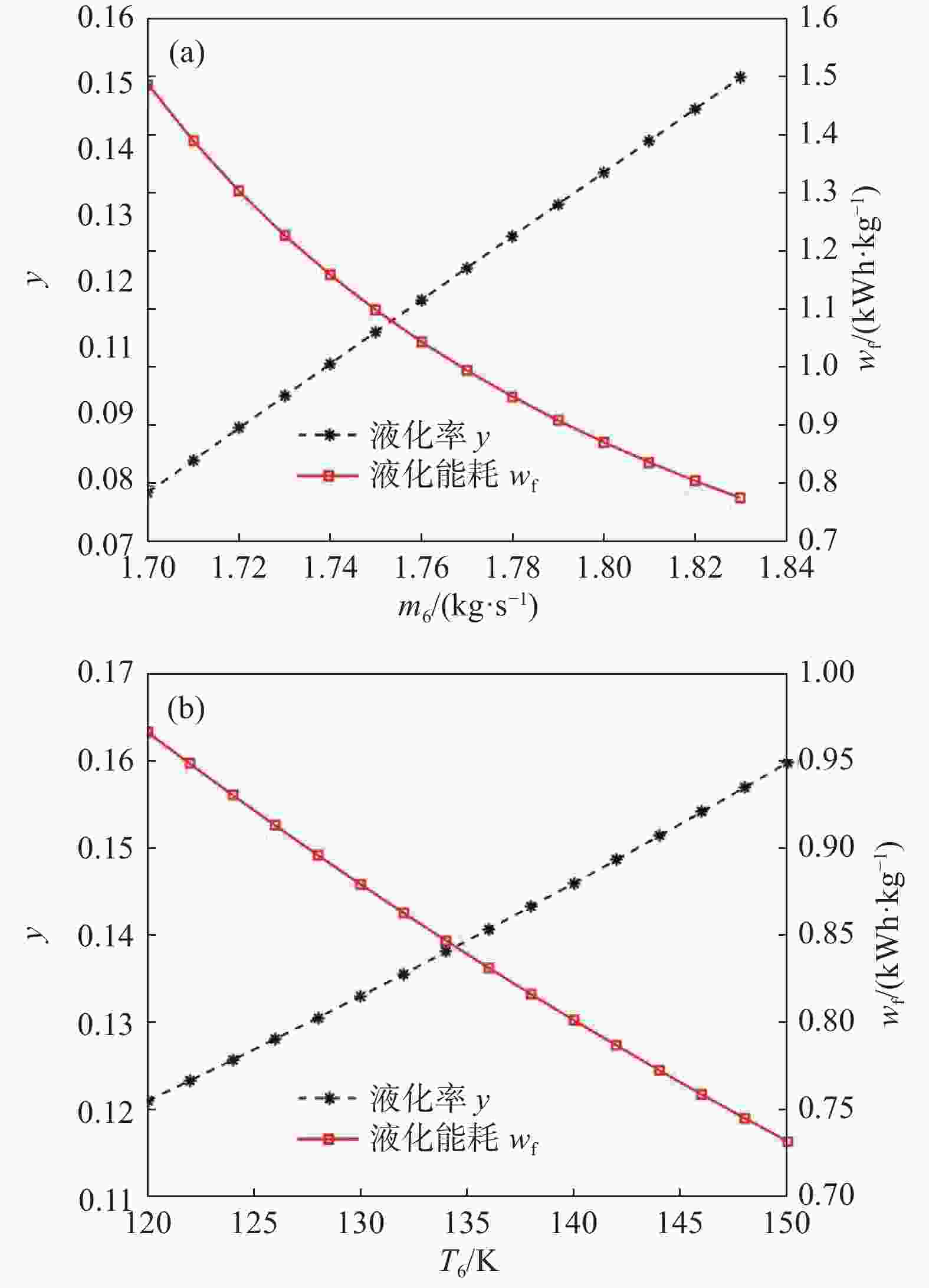
增压膨胀机分流量m₆和入口温度T₆是影响储能过程制冷量的关键参数。图7(a)表明随着m₆增大，液化率几乎线性增加，液化能耗下降且下降速率逐渐减小。m₆增加使增压膨胀机的制冷量增加，从而将节流前的空气（状态点12）预冷至更低温度，使液化率更高。同时，m₆增加使循环压缩机流量增加、主压缩机流量减少，总体来看压缩机组功率略微下降。得益于液化率升高，因此液化能耗降低。值得注意的是，1.83 kg/s是m₆的上限，再增加m₆将导致节流前温度低于空气转化曲线的下限，导致节流产生制热效应。中试装置将m₆设置为1.8 kg/s是合适的选择。保持m₆为1.8 kg/s，逐渐增大T₆，液化率近似线性增加，同时液化能耗线性下降，如图7(b)所示。增压膨胀机入口温度越高使其制冷量增加、做功能力增强，有利于空气液化。中试装置增压膨胀机入口温度为130.55 K，在不影响主换热器传热温差的前提下可以适当提高该温度。

Figure 7.  Influence of inlet flow (a) and inlet temperature (b) of cryogenic expander

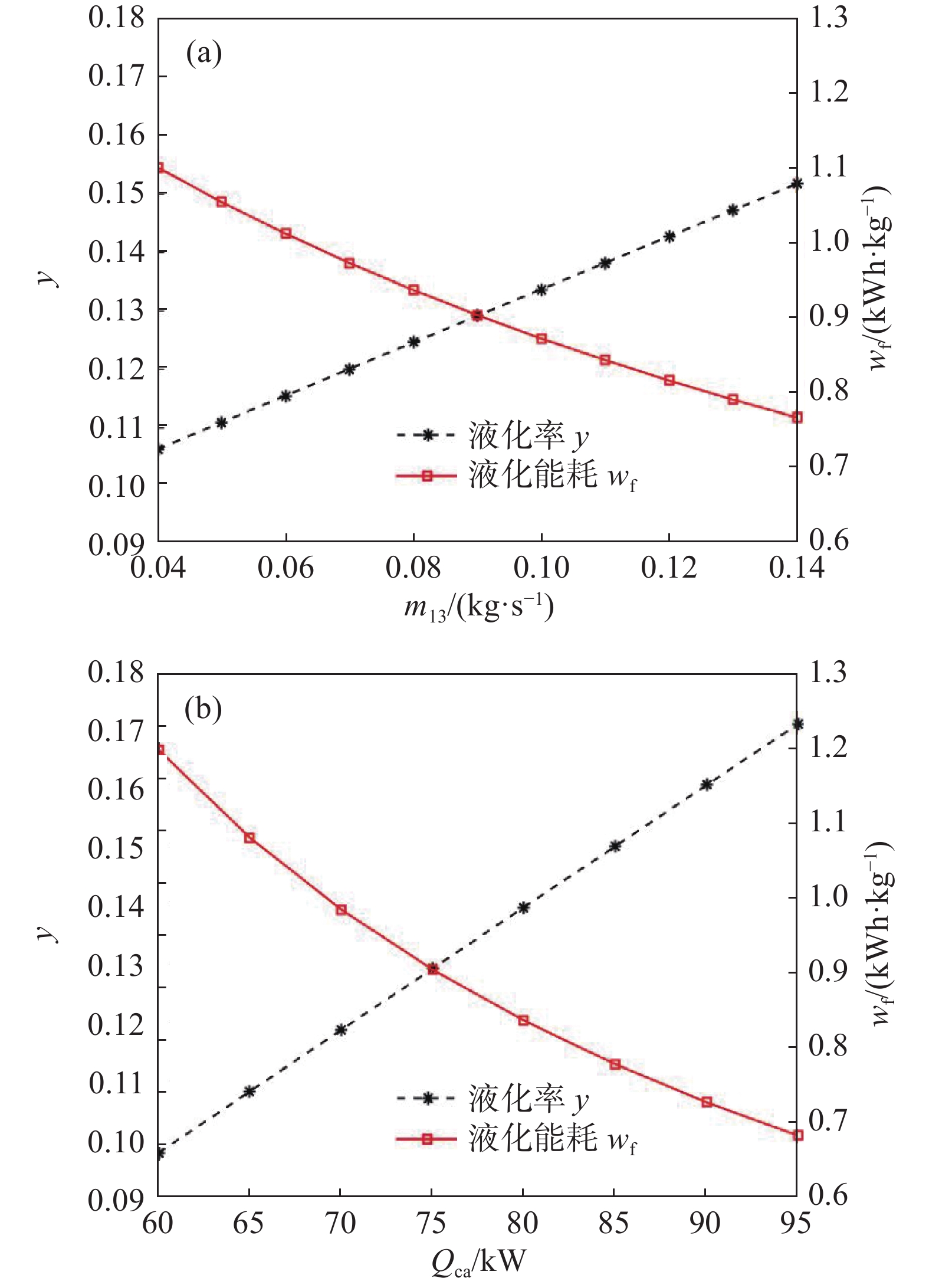
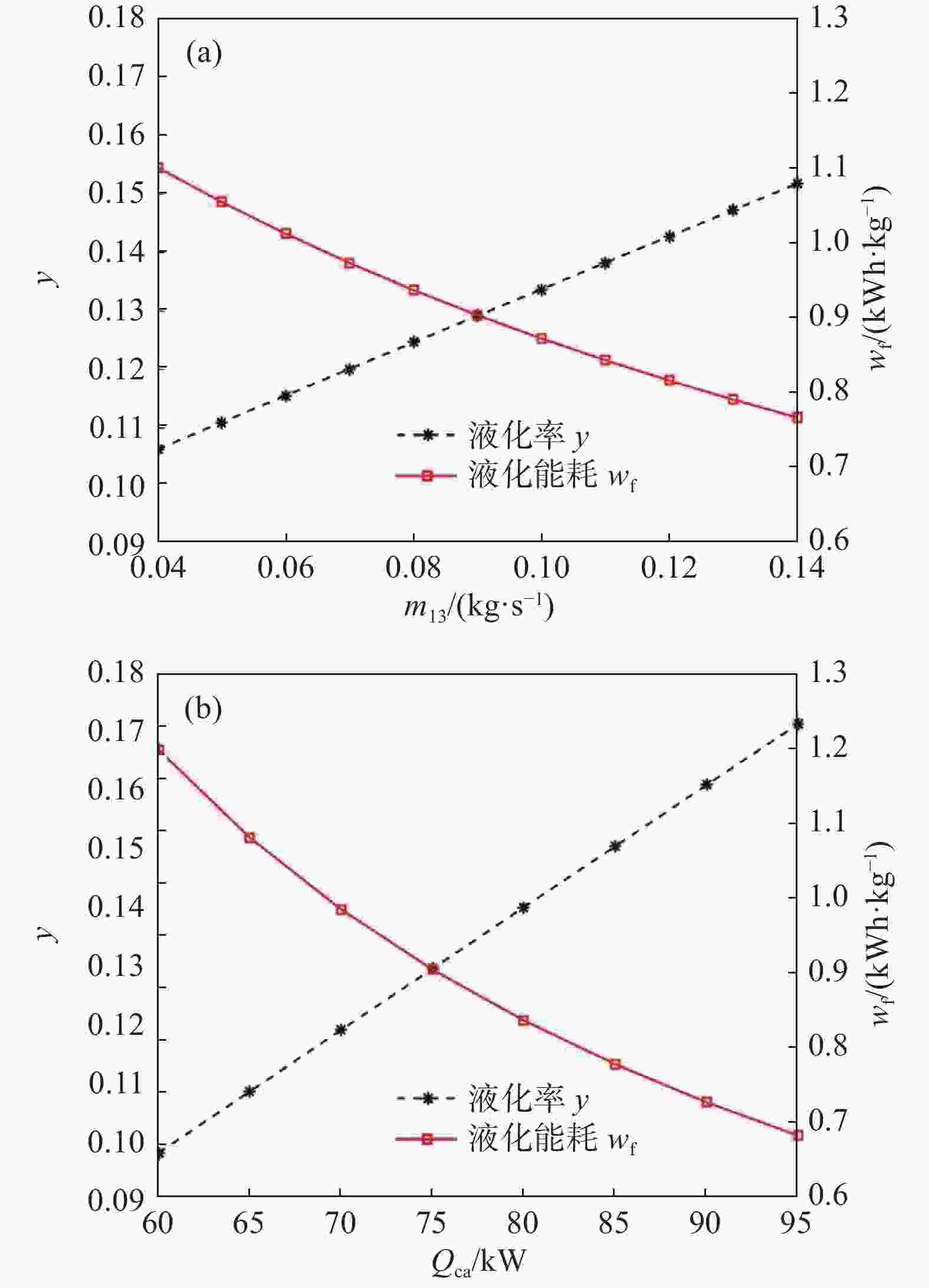
中试装置区别于克劳德循环的另一独特之处在于分出一小股流体节流制冷（状态点13），将高压空气在过冷换热器中进一步预冷。节流制冷流量m₁₃对液化率和液化能耗的影响如图8(a)所示，随着m₁₃增大，液化率线性增加，液化能耗逐渐降低。对比图8(a)和图7(a)，不难发现m₁₃和m₆的影响规律是一致的。分流的m₁₃和m₆都发挥制冷作用，由于增压膨胀机的不可逆损失比节流阀更小，因此大部分制冷量由增压膨胀机提供。除上述两部分制冷量之外，储能过程还有一部分制冷量为蓄冷量Q_cs。蓄冷量越大则液化率越高、液化能耗越低，如图8(b)所示。蓄冷量来自释能过程的汽化器，仅回收了110 K到180 K的冷量88.4 kW，被储能过程利用了77.1 kW。回热器所具有的180 K到254 K的冷量（35.6 kW）被加热器6消耗，实际上被浪费了。若将释能过程回热器的冷量回收，可进一步提升液化率、降低液化能耗。

Figure 8.  Effect of throttling mass flow (a) and cold storage capacity (b)

为方便比较上述具有不同量纲的参数对储能过程的影响程度，将这些参数无量纲化，用液化能耗的变化率和参数变化率比值的绝对值来表示各关键参数的影响程度。这些无量纲比值越大说明该参数对系统性能的影响程度越大。如表6所示，储能过程中对液化能耗影响最大的关键参数是增压膨胀机分流量m₆，影响最小的参数是节流后压力p₁₉。在进行设计优化时，应优先保证增压膨胀机分流量m₆在最优取值区间。

释能过程即液空汽化发电过程，其最重要的评价指标是输出功率。根据输出功率和液化过程的能耗可以计算得到LAES循环效率。释能过程的独立变量有释能高压压力p₂₂和4台膨胀机的入口温度T₂₅、T₂₇、T₂₉、T₃₁。为简化分析，将4台膨胀机入口温度视为一致T_t,in。从而释能过程的关键参数仅p₂₂和T_t,in两个。通过控制变量法分析上述两个关键参数对输出功率和循环效率的影响，参数设置范围见表7。

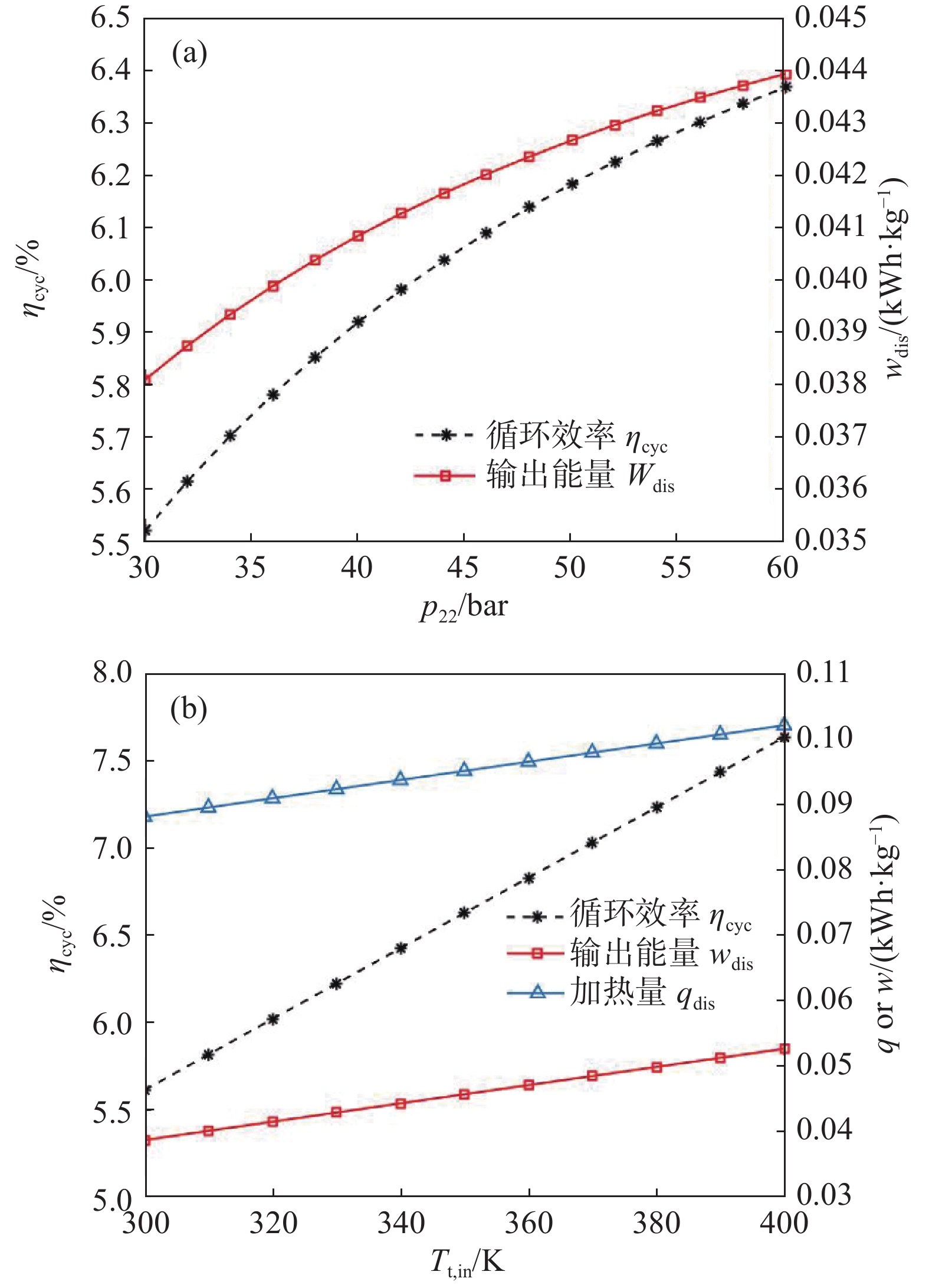
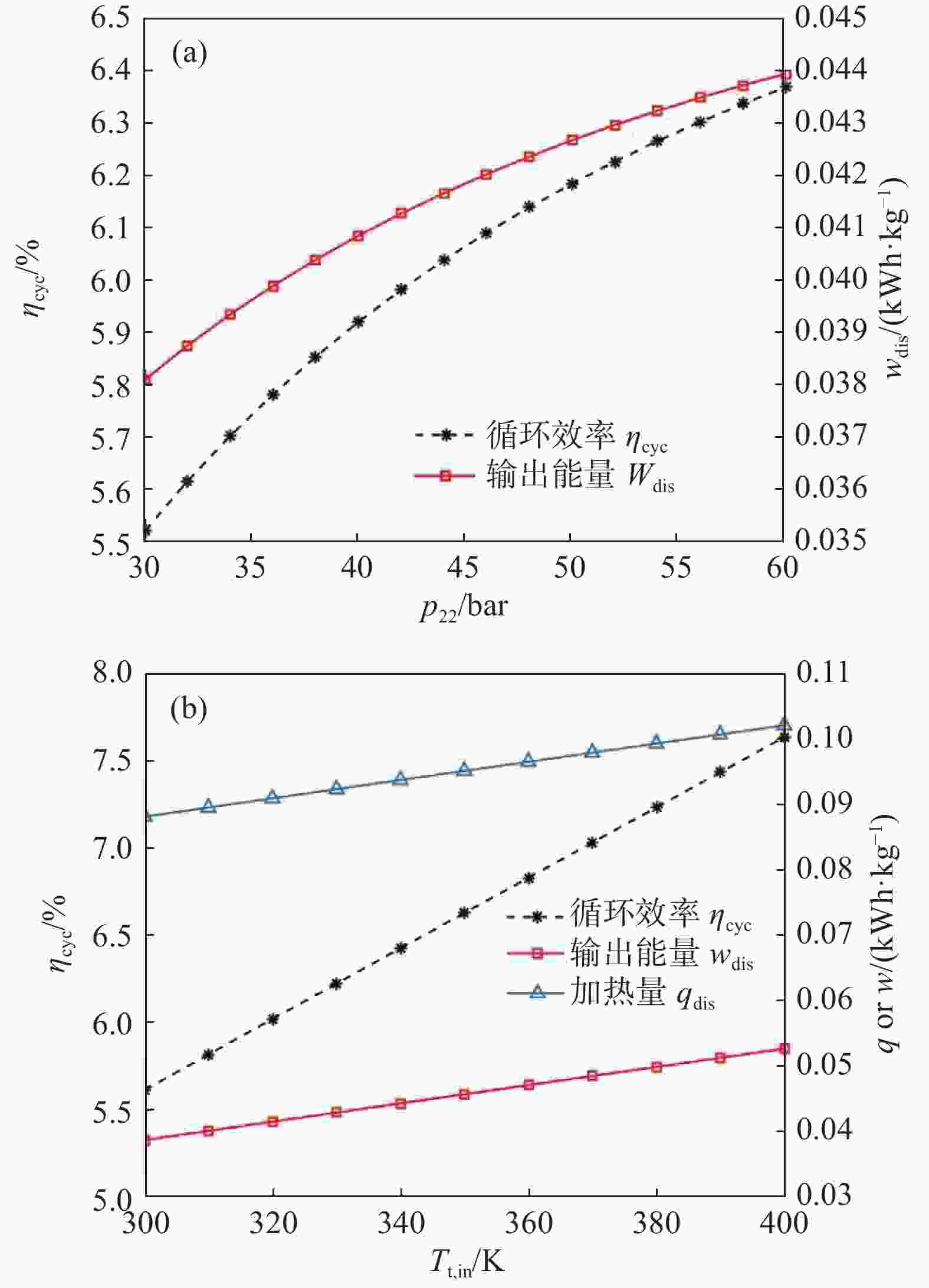
释能高压压力p₂₂直接决定了膨胀机组的入口压力，图9(a)表明p₂₂越高释能过程输出功率越大，循环效率越高。同时，p₂₂越高将使状态点22的比焓越大，导致汽化器可回收的冷量越少，因此循环效率的增速逐渐减缓。图9(b)表明膨胀机入口温度越高，释能过程输出功率越大，循环效率越高。同时，对加热量的需求也越大。中试装置的膨胀机级间再热由60 ℃的发电厂余热供热，因此膨胀机入口温度不到330 K，限制了膨胀机的输出功率。另一方面，压缩机组的放热量（972 kW）并未加以利用。将压缩机组放热量中高于60 ℃的部分加以利用，提高膨胀机入口温度，可以有效提升释能输出功率和循环效率。

Figure 9.  Effect of high pressure of discharge (a) and expander inlet temperature (b)

用单位做功量的变化率和参数变化率的比值表示各关键参数的影响程度。计算结果如表8所示，释能过程中对单位做功量影响最大的关键参数是膨胀机入口温度T_t,in，在进行设计优化时，应优先保证T_t,in在最优取值区间。

在上述控制变量法的基础上，中试装置8个关键参数的初步优化结果见表9。优化后的储能过程运行在更低压力，一方面降低了压缩机能耗，另一方面以更低压力储存液空更安全可靠；优化后的释能过程运行在更高的压力和温度，以增加做功量。中试装置的循环效率从6%提高到8.4%。尽管循环效率有了一定程度的提升，但仍然很低，主要受限于工艺流程，比如压缩热未利用、180 K到254 K的冷量被浪费等。参考表1中所列循环效率超过40%的LAES系统，中试装置的流程可以在以下方面进行改进：（1）液化循环由克劳德循环调整为卡皮查循环；（2）增加储热循环，用以回收主压缩机和循环压缩机的热量，提升膨胀机入口温度；（3）调整蓄冷循环，用单独的蓄冷回路替代排出气蓄冷的方案，使蓄冷温度不再受限于排出气温度，进一步回收冷量。

文章根据Highview Power液化空气储能中试装置的工艺流程建立了热力学建模，利用公开的测试数据验证了热力学模型的准确性。该中试装置循环效率仅6%，通过㶲分析发现储能过程㶲损最大的设备是循环压缩机，其㶲损占储能过程总㶲损的55.7%；释能过程㶲损最大的设备是汽化器，其㶲损占释能过程总㶲损的42%。回收压缩热、提升压缩机等熵效率、优化汽化器换热温差等措施将有效改善循环效率。

通过控制变量法探究关键操作参数对储能过程液化率、液化能耗、释能过程输出功率、循环效率的影响。结果表明尽量提升增压膨胀机入口温度、回收释能过程回热器的冷量有助于提升储能过程液化率、降低液化能耗；提高释能高压压力和膨胀机组入口温度有助于提升系统的输出功率和循环效率。总结了一组优化后的关键操作参数，使循环效率从6%提高到8.4%。

尽管控制变量法是揭示LAES关键参数影响规律的常用方法，但其局限性在于无法对同类型变量进行优化分配。针对LAES系统开展多参数协同优化值得进一步的研究。此外，中试装置的工艺流程存在一些不足，可以在以下方面进行改进：将液化循环调整为卡皮查循环；增加储热循环回收压缩热；设置单独的蓄冷循环。