Quench Voltage Detection for Superconducting Magnets in Tokamak

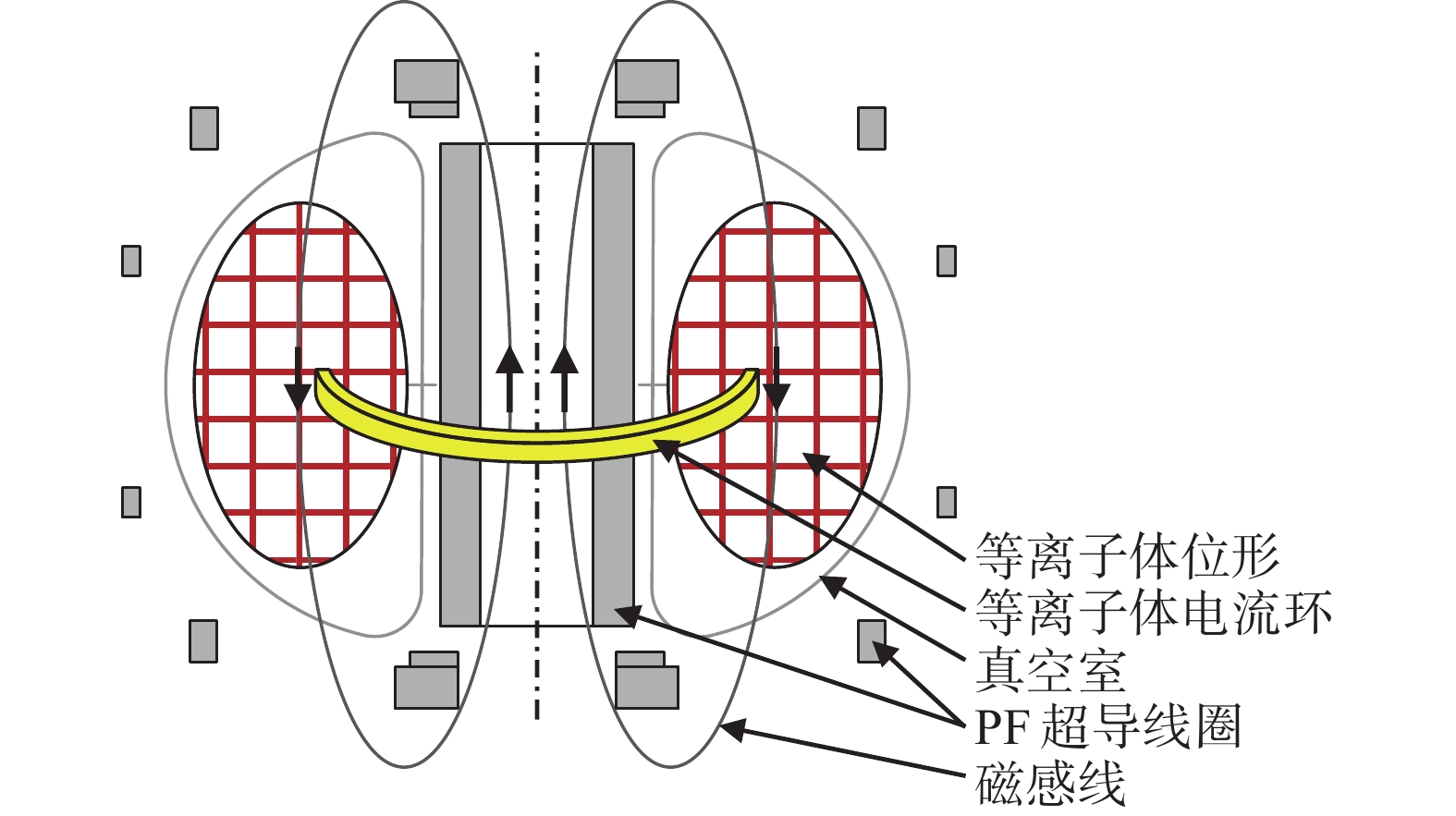
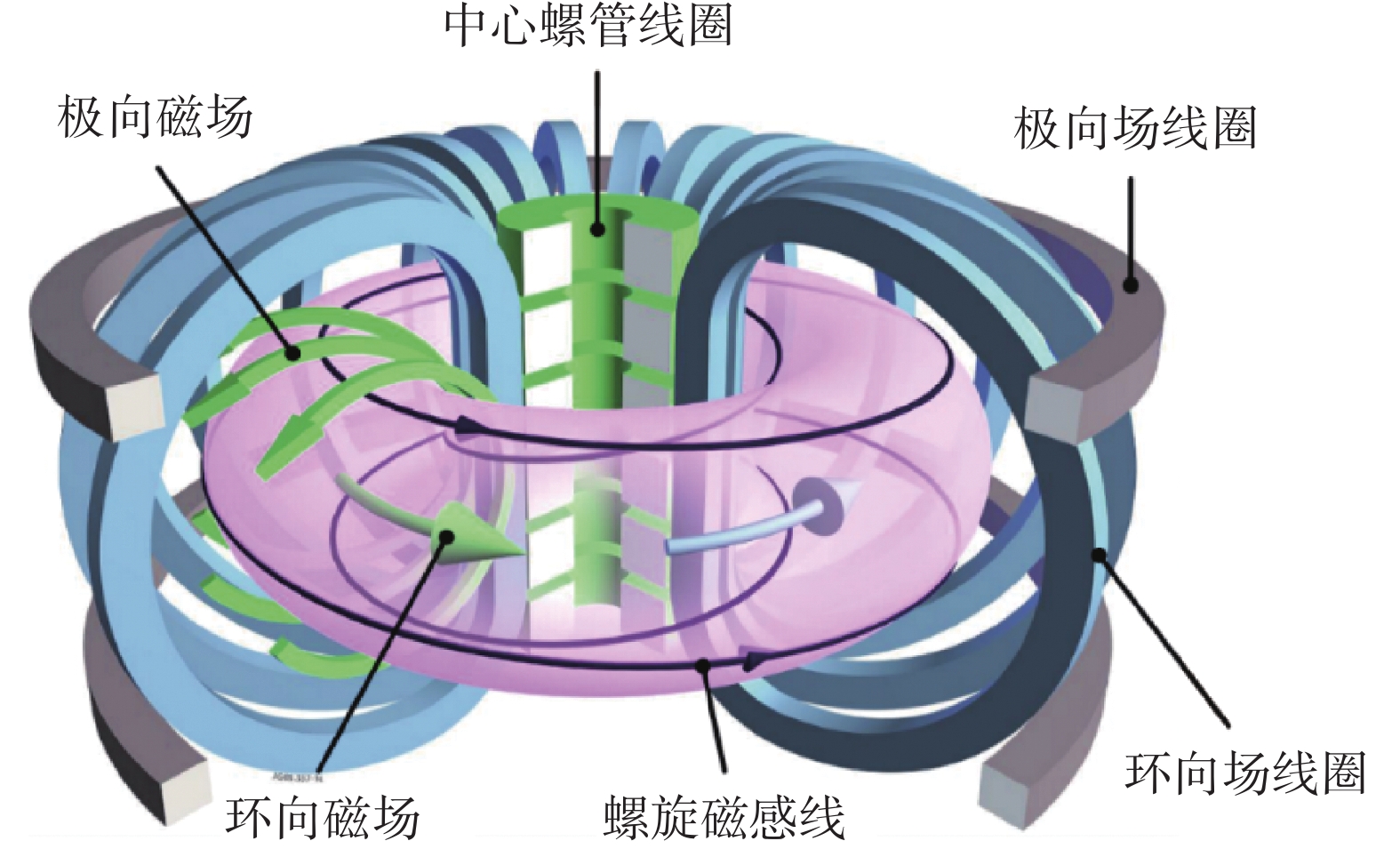
全超导托卡马克是稳态运行的基础，也是未来聚变堆的首选方案^[1]。目前，已建成运行的全超导托卡马克有中国的EAST装置^[2]、韩国的KSTAR装置^[3]和日本的JT-60SA装置^[4]等，尚处于建设中的全超导托卡马克有国际热核聚变实验堆（ITER）^[5]、意大利的DTT装置^[6]和美国的SPARC装置^[7]等。另外，一些国家和组织在各自的聚变能发展路线图中也明确规划建造全超导聚变示范堆，比如中国CFETR项目^[8]、欧盟EU-DEMO项目^[9]、日本JA-DEMO项目^[10]和韩国K-DEMO项目^[11]等。托卡马克超导磁体系统包括纵场线圈、中心螺管线圈和极向场线圈^[12]，其中纵场线圈运行稳态电流产生环向磁场，中心螺管线圈和极向场线圈运行变化电流用于击穿和控制等离子体^[13]，如图1所示。由于运行电流大、磁场高、应力强，托卡马克超导磁体多采用穿管线导体（CICC）绕制^[14]。

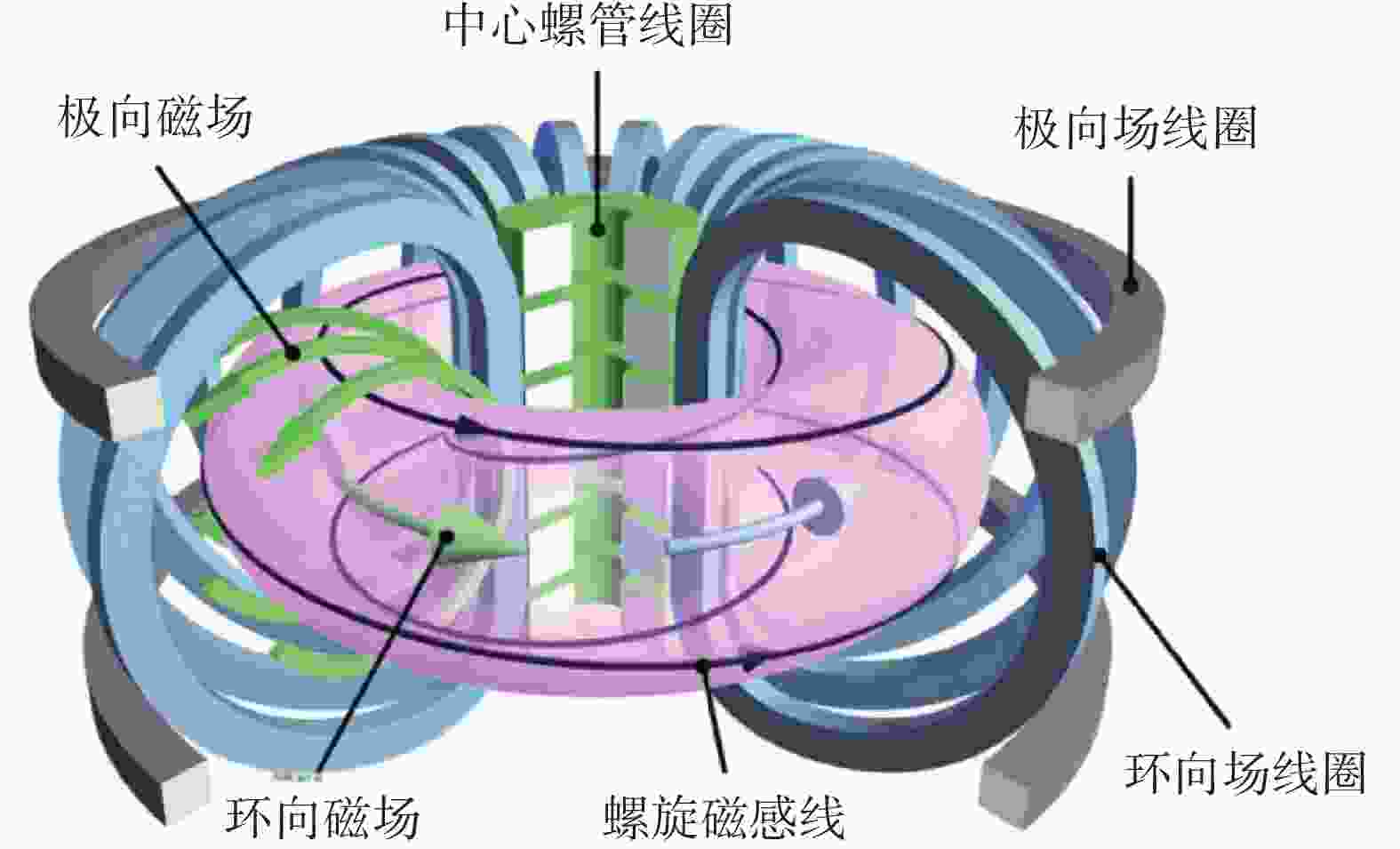
Figure 1.  Superconducting magnet system in tokamak^[15]

超导磁体有临界温度$ {T}_{{\mathrm{c}}} $、临界磁场$ {{\boldsymbol{B}}}_{{\mathrm{c}}} $和临界电流$ {I}_{{\mathrm{c}}} $三个关键参数，当超导磁体的运行温度、磁场和电流均低于临界值时才能处于超导态，其中任一条件不满足都会导致磁体失超^[16-17]。尽管托卡马克超导磁体在设计时留有一定温度裕度^[18]，但运行中任何剧烈的热、电磁和机械扰动都可能导致超导磁体正常区扩展不可控，造成磁体不可恢复失超。随着失超传播，超导磁体电磁储能会通过正常区电阻迅速转化为焦耳热，如不及时探测到失超发生并采取有效的失超保护措施，则会导致局部热点温度过高，进而造成磁体局部损伤^[19]。托卡马克复杂工况下还应保证失超探测的可靠性，避免信号干扰导致失超保护的误触发和磁体性能衰退，例如ITER纵场磁体设计的最大失超保护次数只有50次^[20]。因此，及时、可靠的失超探测是超导磁体运行安全的关键所在，享有托卡马克装置安全的最高等级。

失超探测重点是寻找电压、电流、温度等参量在失超传播过程中的变化规律，由此发展的失超探测方法主要包括：电压检测、温度检测、压力流量检测、主动检测等^[21]。近年来高温超导应用于聚变磁体日趋成熟，但高温超导失超传播速度慢导致传统失超探测方法难以响应及时，因此一些新型失超探测技术应运而生，包括射频波检测技术、光学检测技术、声学检测技术和磁场检测技术等，相关研究目前仍以导体短样和小线圈为实验对象，尚未发展到可应用于大型聚变磁体的成熟阶段^[22]。

电压检测由于响应迅速通常被用作聚变磁体的主失超探测方案，但在托卡马克复杂电磁环境下容易受到感应电压干扰，需要针对感应电压进行补偿抑噪以保证失超探测的可靠性。EAST作为首个全超导托卡马克实验装置，其采用电压检测作为主失超探测方案，并通过同绕补偿线圈和信号运算处理两级解耦补偿对感应电压进行抑制，以满足信噪比要求^[23]。KSTAR主失超探测同样采用电压检测方案，并分别采用同绕补偿线圈和桥路补偿方案对不同线圈的失超探测信号进行噪声抑制^[24]。ITER拥有当前规模最大的超导磁体系统，对失超探测可靠性要求更高，失超探测电压信号在经同绕补偿线圈抑噪后，再利用磁体绕组的对称性进行桥路补偿，以实现高噪声抑制比^[25]。文章聚焦于失超电压探测方案，从探测原理、干扰分析、补偿方法等方面总结相关研究进展，对聚变磁体失超电压探测设计具有参考意义。

失超是指导体从超导态向正常态的不可逆转变过程，由于失超区域的超导股线电阻率大于铜股线，所以失超导体的电流会从超导股线分流到铜股线中，并会产生大量的焦耳热，使失超热点温度不断升高。伴随热量累积，正常区域沿着CICC导体方向传播，其速度称之为失超传播速度。随着失超区域的持续传播扩大，正常区域电阻也随之增加，由于运行电流存在，产生的失超电压也会从零逐渐增大，失超电压探测就是根据这个电压变化来判别失超发生并采取保护措施。以电压检测作为聚变磁体的主失超探测方案，具有如下优点：（1）任何局部失超产生的电阻电压都可通过磁体端电压进行检测，因此可以通过简单电路实现全域探测；（2）由于失超电压零延迟，可以实现及时失超探测。

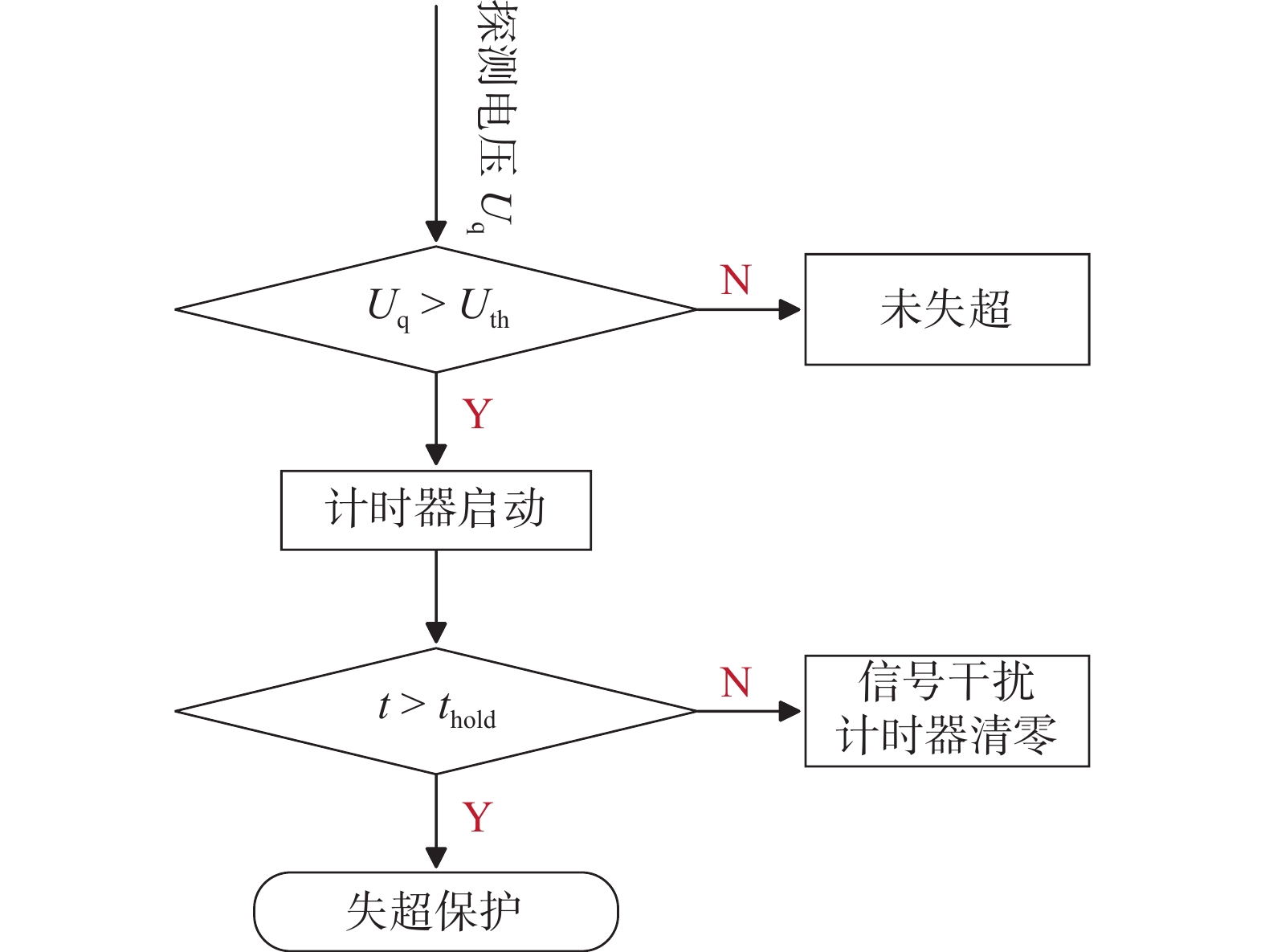
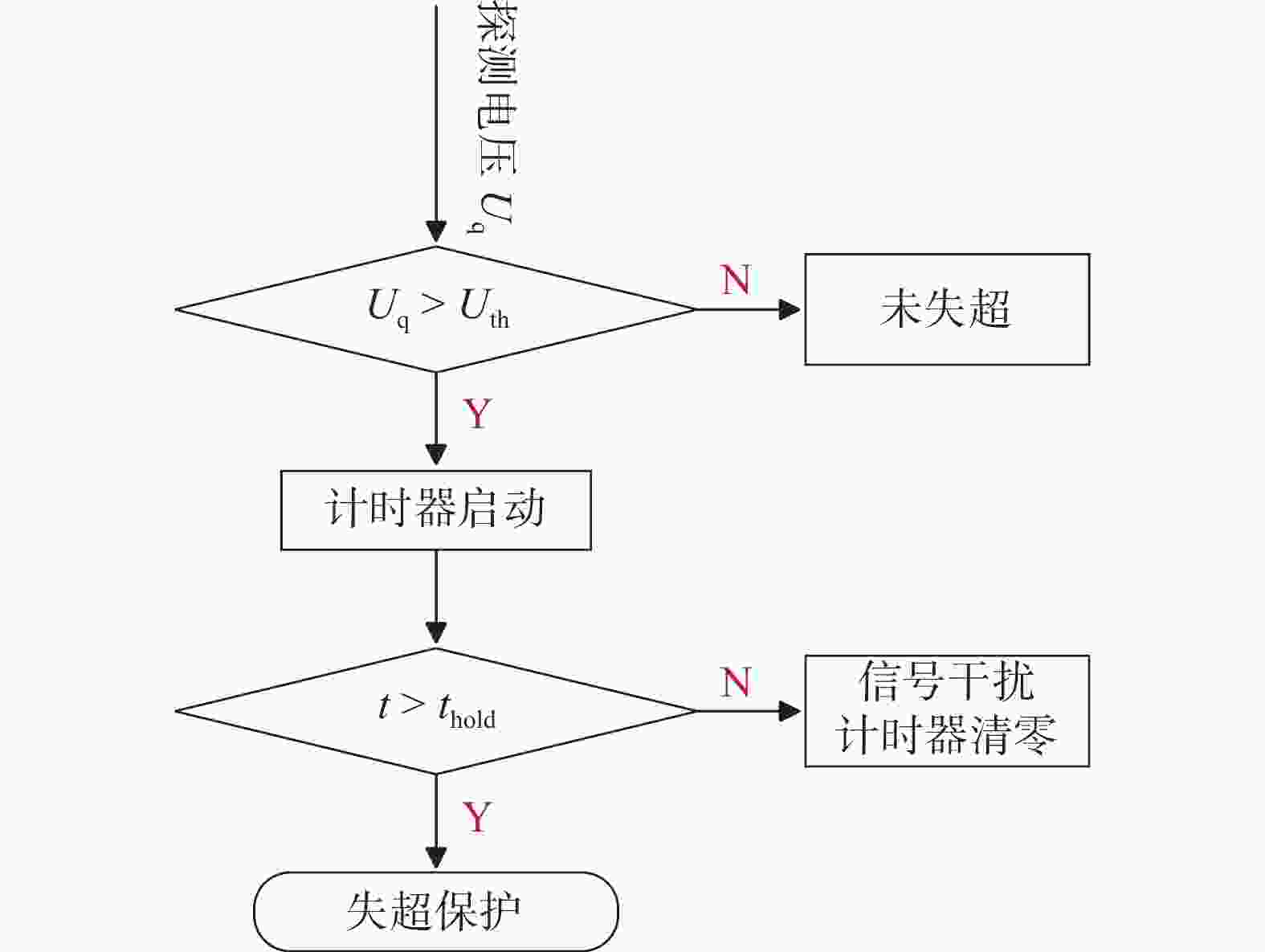
失超过程并不是一瞬间完成的，而且失超电压探测会受到各种干扰，因此失超逻辑判别需要设定电压阈值$ {U}_{{\mathrm{th}}} $和时间阈值$ {t}_{{\mathrm{hold}}} $。其中，设置$ {U}_{{\mathrm{th}}} $是为了避免本底电压和残余噪声的干扰，设置$ {t}_{{\mathrm{hold}}} $是防止瞬时电压扰动导致失超保护误触发。因此，对于失超电压探测系统的设计，$ {U}_{{\mathrm{th}}} $和$ {t}_{{\mathrm{hold}}} $的选择直接决定了失超探测系统的灵敏度及可靠性。磁体设计阶段，会根据磁体失超触发条件和传播特性进行失超仿真分析，评估不同失超探测阈值和失超保护参数下失超热点的最高温升，以此来选择合适失超探测阈值，避免失超热点温度过高造成磁体局部损伤。阈值设定后，允许失超探测电压超过电压阈值一段时间，如其持续时间超过了时间阈值，才会判定为失超并触发保护机制，如图2所示。

Figure 2.  Quench logical discrimination mechanism

由于聚变磁体运行电流大、储能高，一旦失超会通过外接移能电阻的方式将磁体储能快速泄放。因此失超泄放电路可以简化为磁体电感和移能电阻串联的RL电路，其快速泄放时间常数可描述如下：

式中：

$ {L}_{{\mathrm{SC}}} $ ——磁体电感（H）；

$ {R}_{{\mathrm{D}}} $ ——移能电阻（Ω）。

$ {\tau }_{{\mathrm{FD}}} $是失超保护关键参数之一，对于特定磁体而言，$ {\tau }_{{\mathrm{FD}}} $越小能量泄放越快、失超热点温升越低，但由于快速泄放导致的磁体端电压越高，因此该参数需要平衡失超保护和磁体绝缘综合选择。

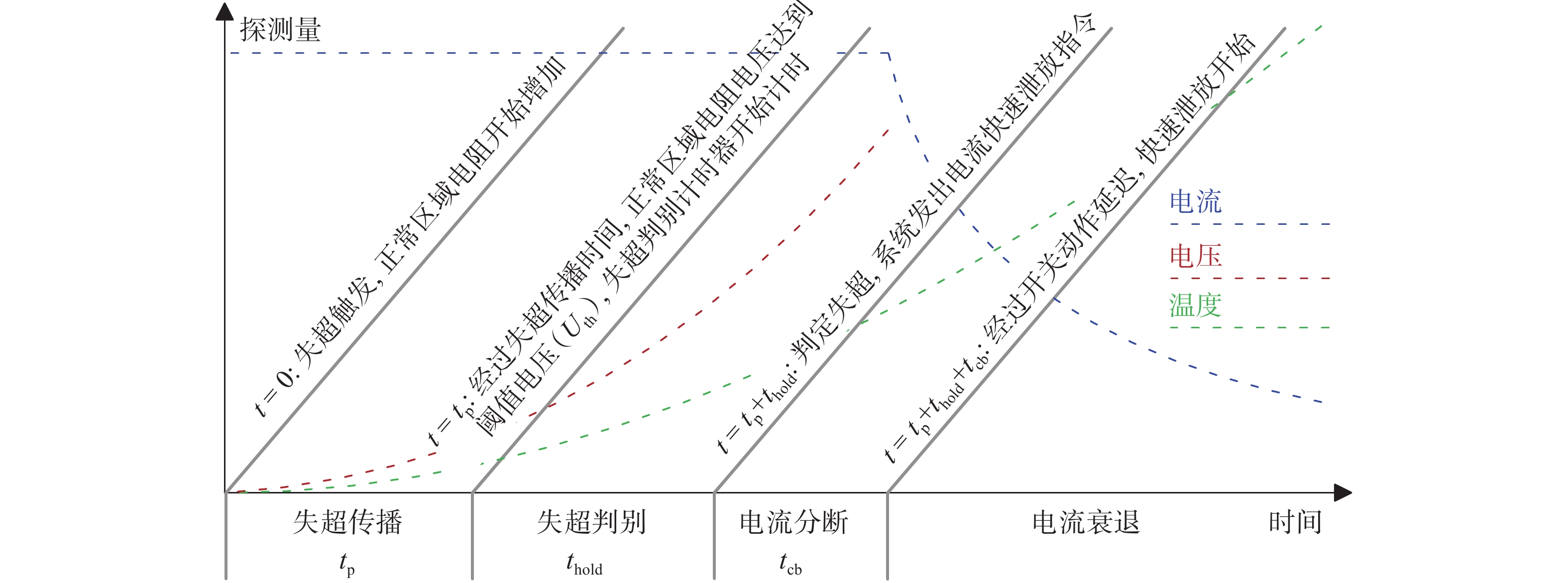
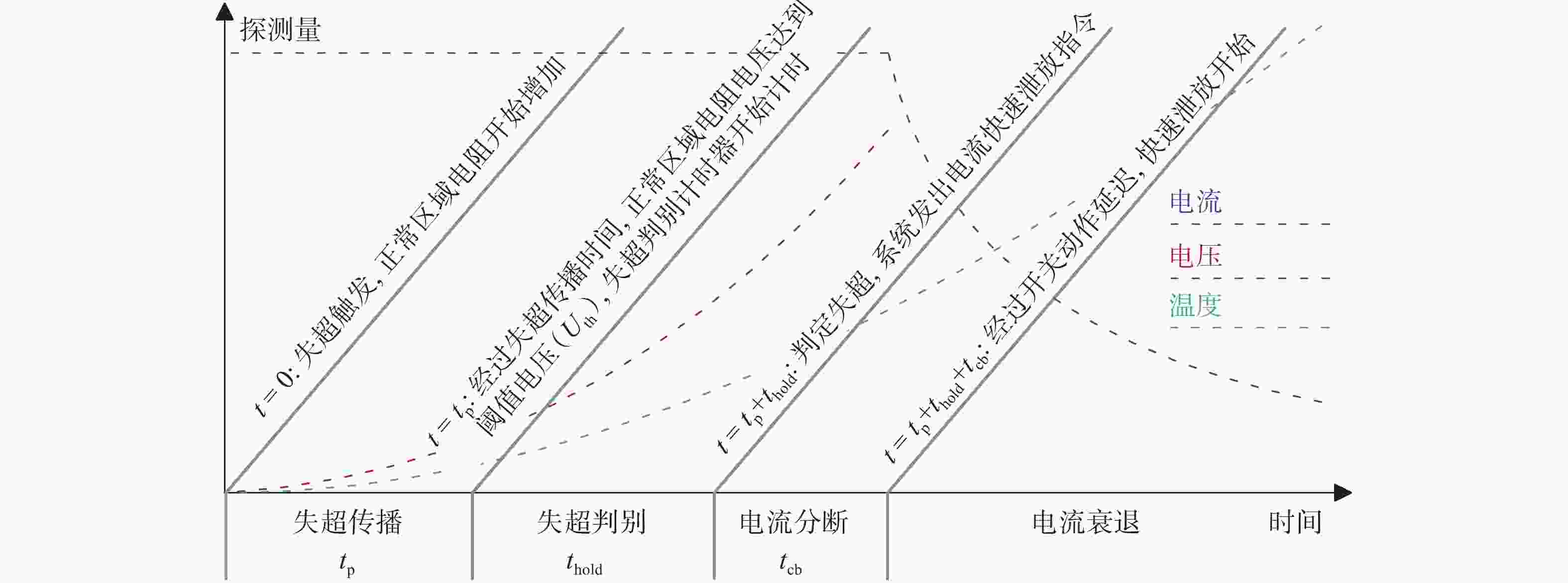
失超电压探测过程可以细分为失超传播、失超判别、电流分断、电流衰退4个阶段，如图3所示。失超触发后，随着失超传播探测电压逐渐上升，直至达到$ {U}_{{\mathrm{th}}} $计时器开始计时，该阶段所用时间称之为失超传播时间$ {t}_{{\mathrm{p}}} $。在失超判别阶段，如果失超探测电压下降到$ {U}_{{\mathrm{th}}} $以下，则计时器被重置归零直至下一次探测电压达到$ {U}_{{\mathrm{th}}} $重新开始计时，否则计时器一直在累加说明失超区域仍在扩大，失超热点仍在升温。当计时器累加时间达到$ {t}_{{\mathrm{hold}}} $后，失超判别条件成立，失超探测系统立即发出快速泄放指令。但由于聚变磁体运行电流高达数万安培，从电源主回路切换至快速泄放回路需要一定时间，称之为电流关断时间$ {t}_{{\mathrm{cb}}} $。切换到快速泄放回路后，磁体电流呈指数衰减，此时磁体储能通过外接移能电阻快速转化为热能并释放，从而避免磁体失超热点温度过高。通过上述分析，整个失超探测过程中，总延迟时间为：

Figure 3.  Process of quench voltage detection

式中：

$ {t}_{{\mathrm{p}}} $ ——失超传播时间（s）；

$ {t}_{{\mathrm{hold}}} $ ——失超判别阈值时间（s）；

$ {t}_{{\mathrm{cb}}} $ ——电流关断时间（s）。

根据ITER失超探测的设计标准，失超探测及电流快速泄放过程中，CICC导体铠甲的失超热点温度不应超过150 K，以保证磁体及绝缘的安全^[26]。

托卡马克装置复杂的电磁环境对失超电压探测的可靠性带来极大挑战，因为超导磁体端电压中巨大的感应电压会将微弱的失超电阻电压淹没^[27]。对EAST失超探测技术而言，需要提取出千分之一的真实信号，即近千伏感应电压噪声下，1～2 s内准确识别百毫伏量级的真实失超电压信号；而未来聚变装置则需要在千伏感应电压噪声下，做出同样的精准探测。

从噪声来源分析，造成失超电压探测电磁干扰的原因有：磁体间相互耦合，特别是中心螺线管线圈与极向场线圈间的相互耦合，磁体运行电流快速变化时会产生感应电压干扰；磁体与等离子体间耦合，等离子体电流爬升、下降以及快速变化事件会造成感应电压扰动；磁体与无源结构件间的耦合，例如真空室组件中的涡流变化也会对磁体产生感应电压干扰。以极向场线圈为例，其端电压组成如下：

式中：

$ {R}_{j} $ ——接头电阻（Ω）；

$ {R}_{{\mathrm{q}}}\left(t\right) $ ——失超电阻（Ω）；

$ {I}_{i}\left(t\right) $ ——线圈$ i $的运行电流（A）；

$ {L}_{i} $ ——线圈$ i $的自感（H）；

$ {M}_{ij} $ ——线圈$ i $与线圈$ j $间的互感（H）；

$ N $ ——线圈的数量；

$ {I}_{j}\left(t\right) $ ——其他线圈的运行电流（A）；

$ {M}_{i-I_{\mathrm{p}}}\left(t\right) $ ——线圈$ i $与等离子体间的动态耦合电感（H）；

$ {I}_{{\mathrm{p}}}\left(t\right) $ ——等离子体电流（A）；

$ M_{i-\mathrm{\mathit{j}vv}} $ ——线圈$ i $与组件涡流间耦合电感（H）；

$ I_{\mathrm{\mathit{j}vv}}\left(t\right) $ ——组件涡流（A）。

式（3）右侧第1项为电阻电压，第2项和第3项分别为线圈自感和互感耦合电压，第4项和第5项为等离子体耦合电压，第6项为组件涡流耦合电压。为避免耦合干扰造成失超探测的误判和误触发，需要针对各类感应电压进行补偿抵消，以将残余干扰电压降低至电压阈值以下。

尽管托卡马克中干扰源繁多复杂，但所有干扰源空间磁场可以分为极向和环向分量，并可通过耦合机理分析计算其耦合电感。极向磁通（$ {\varPhi }_{{\mathrm{p}}} $）变化对中心螺管线圈和极向场线圈的绕组产生耦合电压，同时对纵场线圈的CICC导体绞缆结构产生耦合电压；环向磁通（$ {\varPhi }_{{\text{φ}}} $）变化对纵场线圈的绕组产生耦合电压，并对中心螺管线圈和极向场线圈的CICC导体绞缆结构产生耦合电压，如表1所示。

但与磁体间耦合机理不同的是，受时变位形等约束参数的影响，等离子体与超导磁体间耦合电感呈现动态特性。托卡马克装置中等离子体的感应激发和维持是一个能量传递过程，这一过程可以抽象为“变压器”结构，变压器的原边是托卡马克的磁体系统，副边就是被激发的等离子体电流，这种结构将原边磁体中的电磁能转化为等离子体的电磁储能和动能^[28]。另一方面等离子体电流的爬升、下降、抖动和破裂会对磁体耦合出明显的感应电压，从而对失超电压探测微弱信号造成干扰，如不有效抑制则会导致失超探测的误判和误触发。

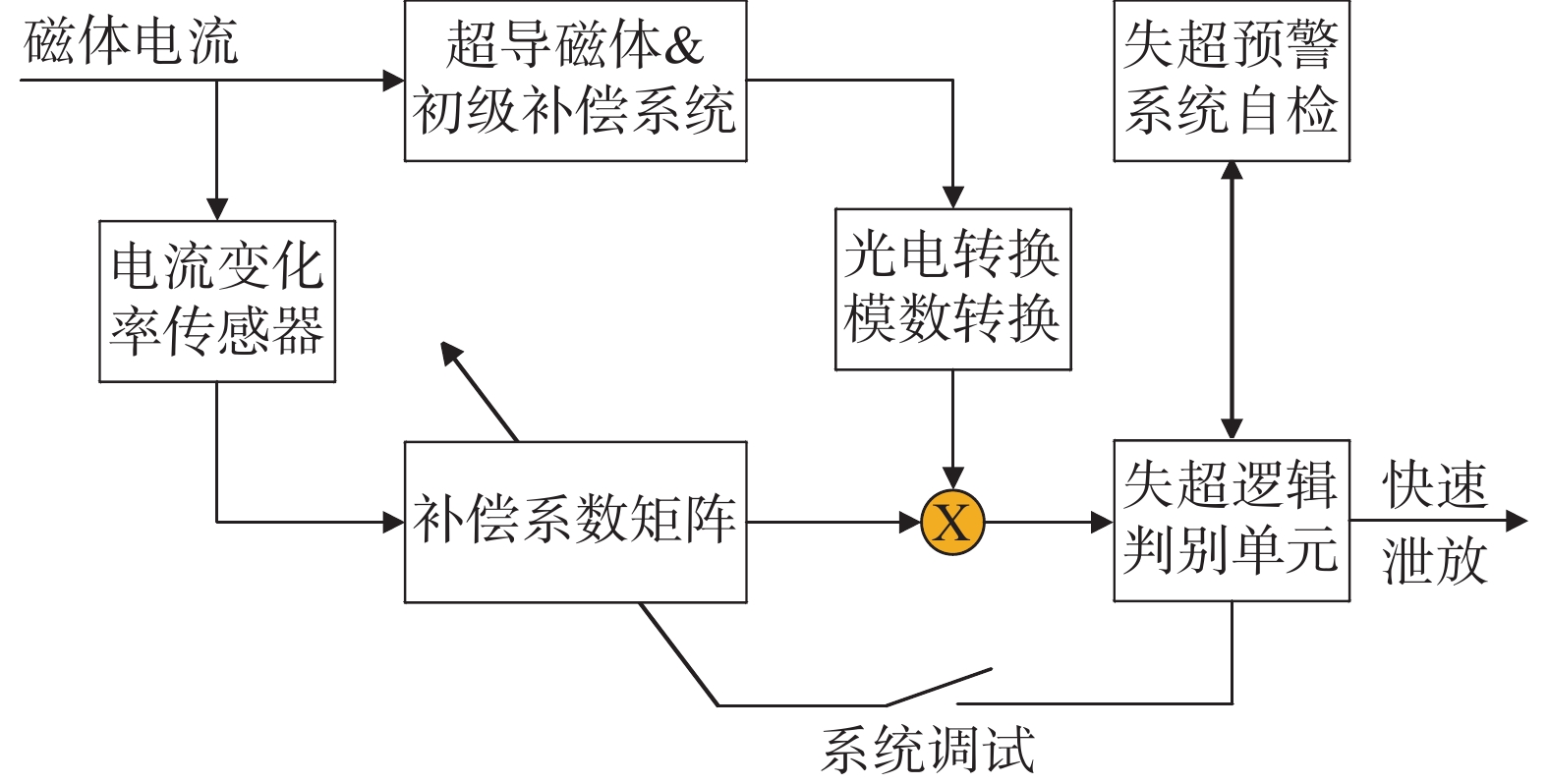
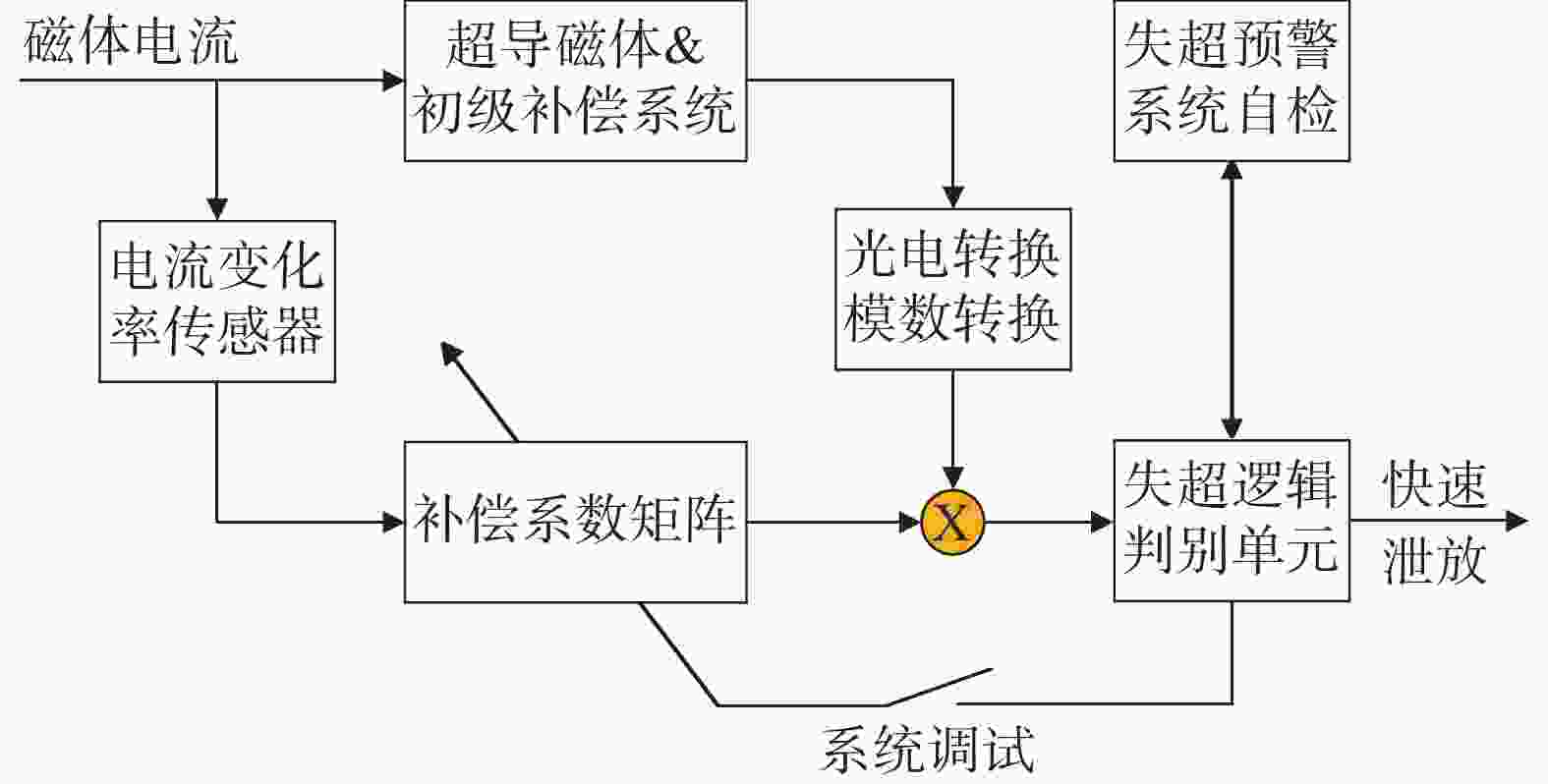
超导托卡马克中，多采用两级补偿方案对失超电压探测信号进行解耦补偿以满足信噪比要求，特别是对于等离子体耦合干扰需要基于约束参数反馈实现动态精准补偿。初级补偿通过测量补偿电路与超导磁体间差分电压实现“自然”解耦补偿，能够抑制95%以上的干扰电压；次级补偿则通过电流互感器测量不同干扰源的电流变化率，并通过信号处理单元将电流变化率乘以补偿系数后与初级补偿后的信号叠加，以进一步抑制干扰电压，如图4所示。

Figure 4.  Structure diagram of interference compensation system for quench voltage detection

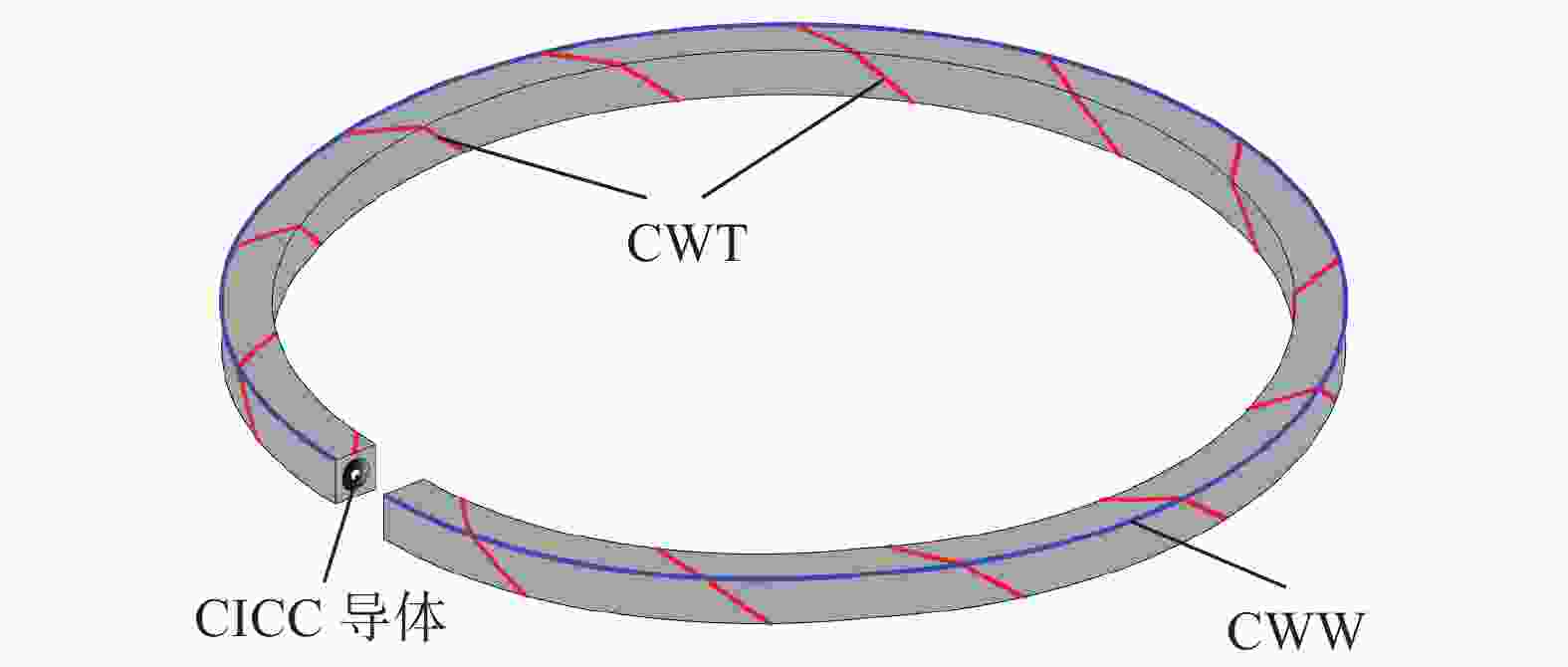
初级补偿采用同绕带（CWT）和同绕线（CWW）组成补偿线圈，二者起到的功能互为冗余以增加系统可靠性。如图5所示，CWT由一根不锈钢带内嵌于玻纤纺织带组成，位于线圈匝间绝缘的第二层，以固定螺距螺旋包绕于CICC导体铠甲外侧；CWW由一根不锈钢线内嵌于玻纤纺织护套组成，位于线圈匝间绝缘外侧，沿着CICC导体铠甲的倒角平行布线。由于CWT和CWW组成的补偿线圈与超导线圈同步绕制，具有几近相同的结构尺寸和耦合电感，与分离式补偿线圈相比能够实现更高的噪声抑制比。

Figure 5.  Installation diagram of CWT and CWW

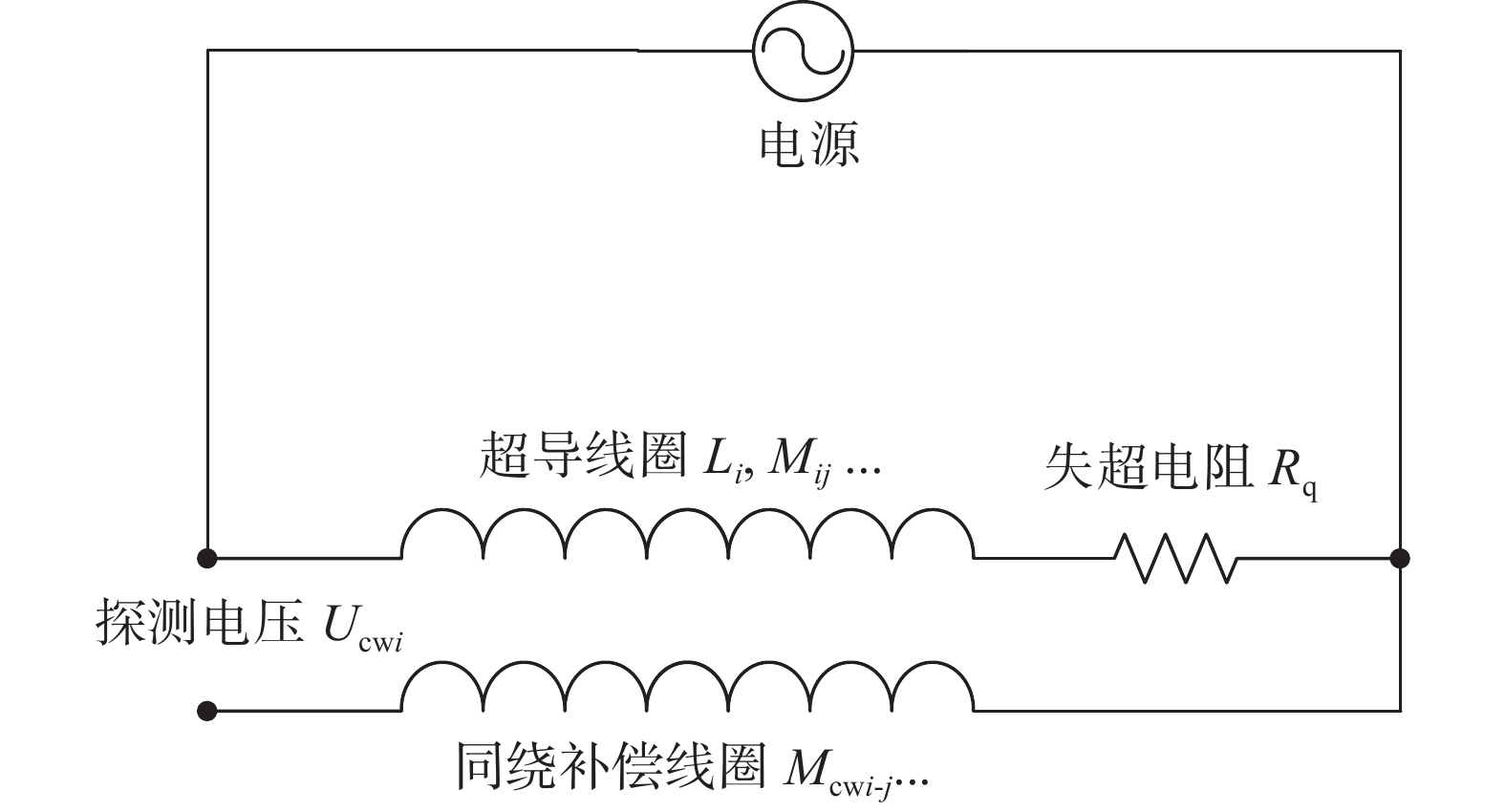
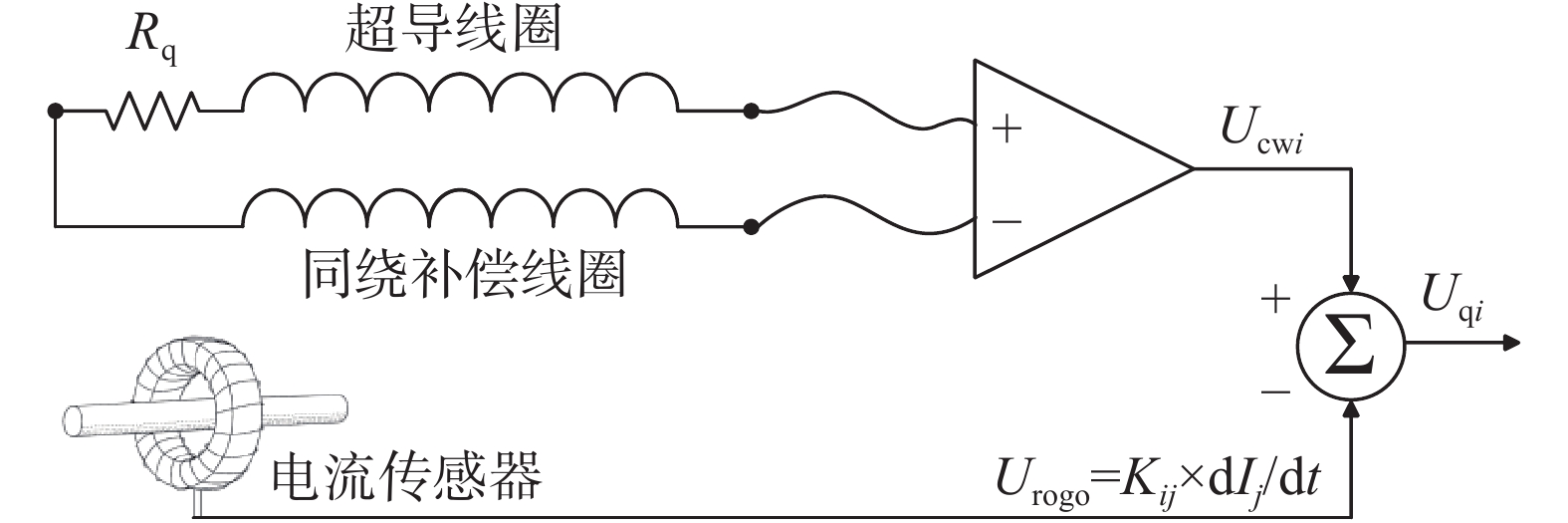
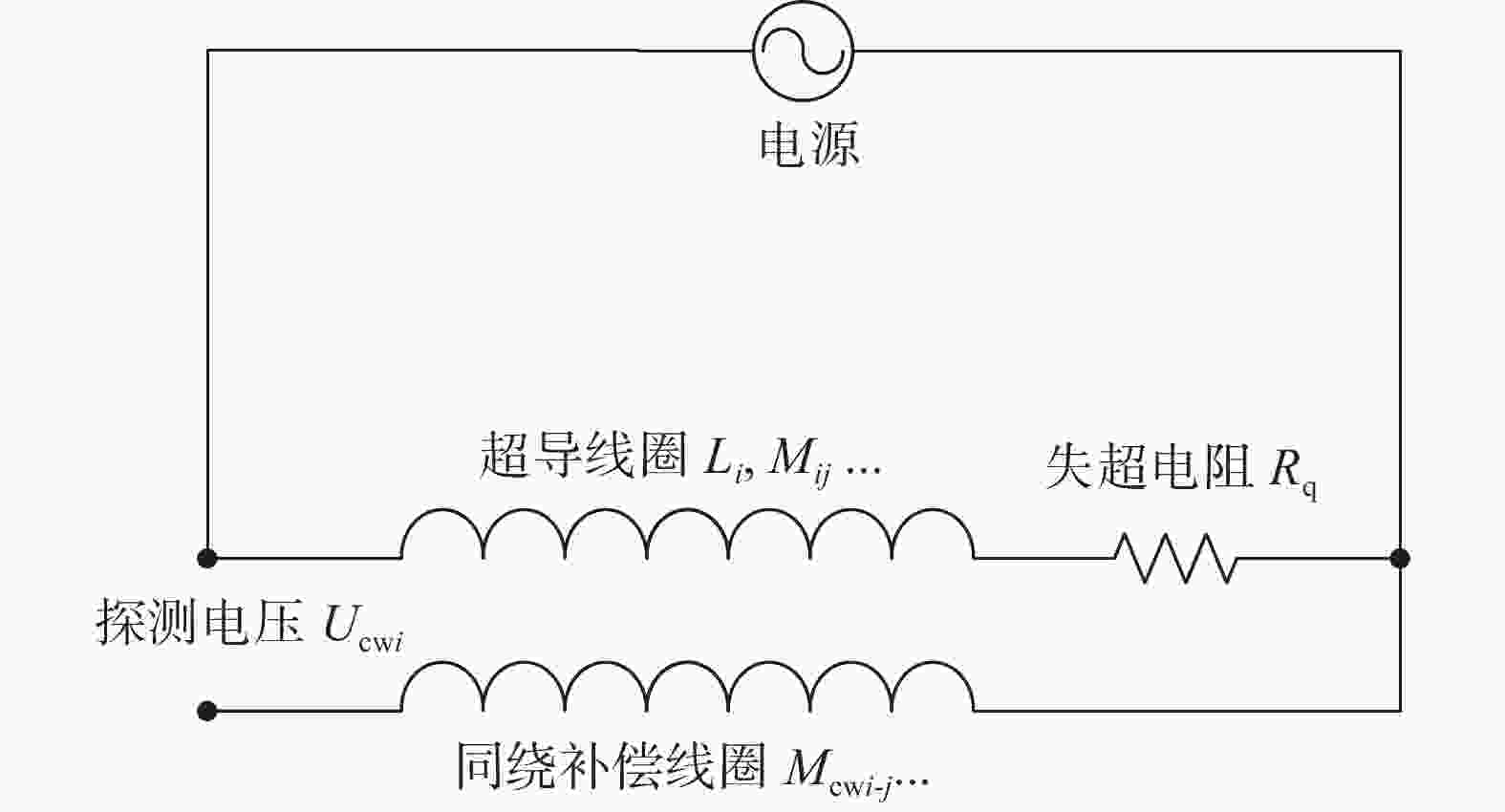
同绕补偿线圈一端与超导线圈连接，并通过另一端测量超导线圈与同绕补偿线圈间的差分电压，如图6所示。由于同绕补偿线圈与超导线圈耦合电感相近，因此其测量信号中感应电压干扰可被很大程度上抑制，初级补偿后的探测电压如下：

Figure 6.  Schematic diagram of the compensation circuit for quench voltage detection

式中：

$ U_{\mathrm{cw\mathit{i}}}\left(t\right) $ ——线圈$ i $初级补偿后的探测电压（V）；

$ M_{\mathrm{cw\mathit{i}}-i} $ ——线圈$ i $的同绕补偿线圈与其自身间耦合互感（H）；

$ M_{\mathrm{cw\mathit{i}}-j} $ ——线圈$ i $的同绕补偿线圈与其他线圈间耦合互感（H）；

$ M_{\mathrm{cw\mathit{i}}-{I_\mathrm{p}}}\left(t\right) $ ——线圈$ i $的同绕补偿线圈与等离子体间动态耦合电感（H）；

$ M_{\mathrm{cw\mathit{i}}-\mathrm{\mathit{j}vv}} $ ——线圈$ i $的同绕补偿线圈与组件涡流间耦合互感（H）。

可见，同绕补偿线圈耦合电感与超导线圈耦合电感的差异是决定补偿效果的关键。

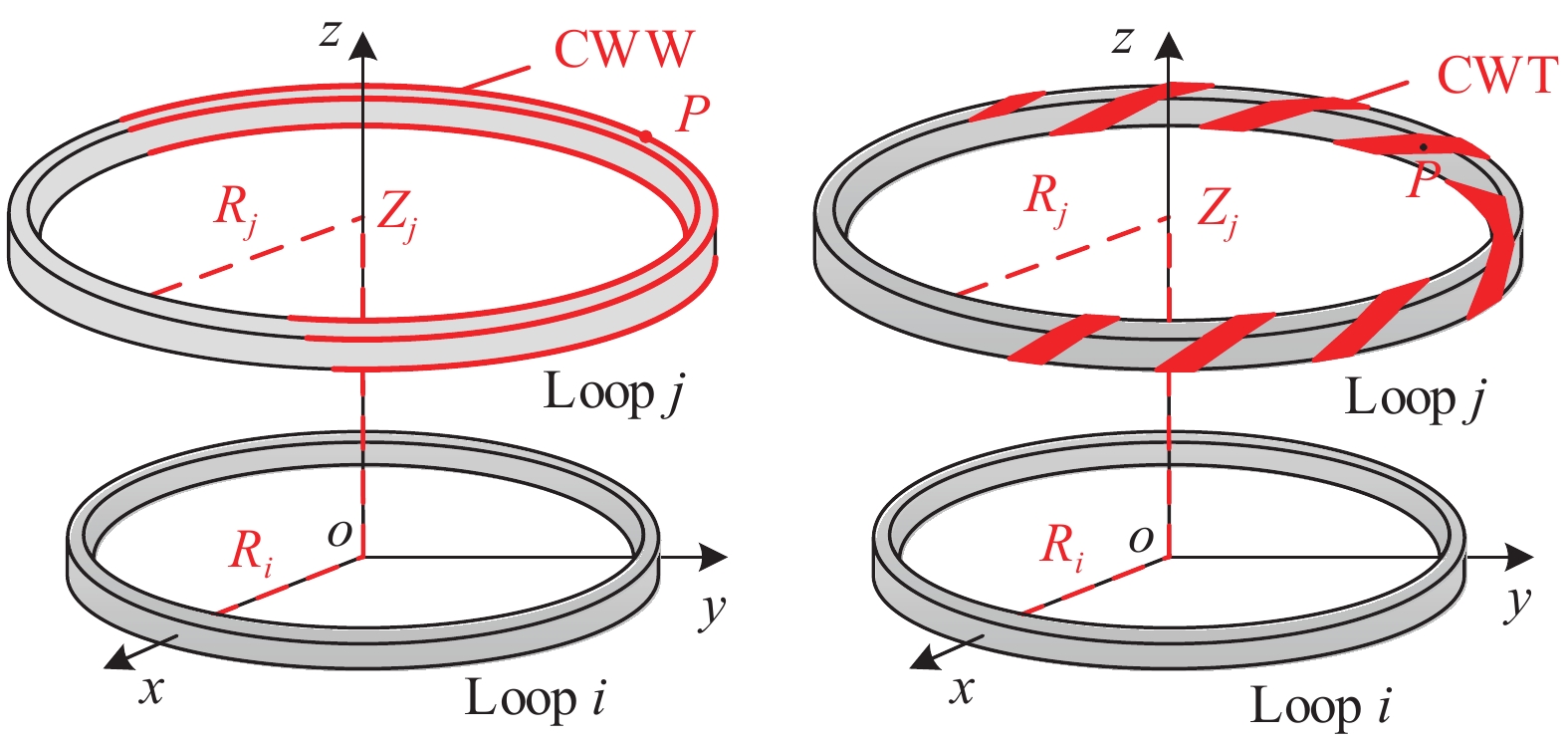
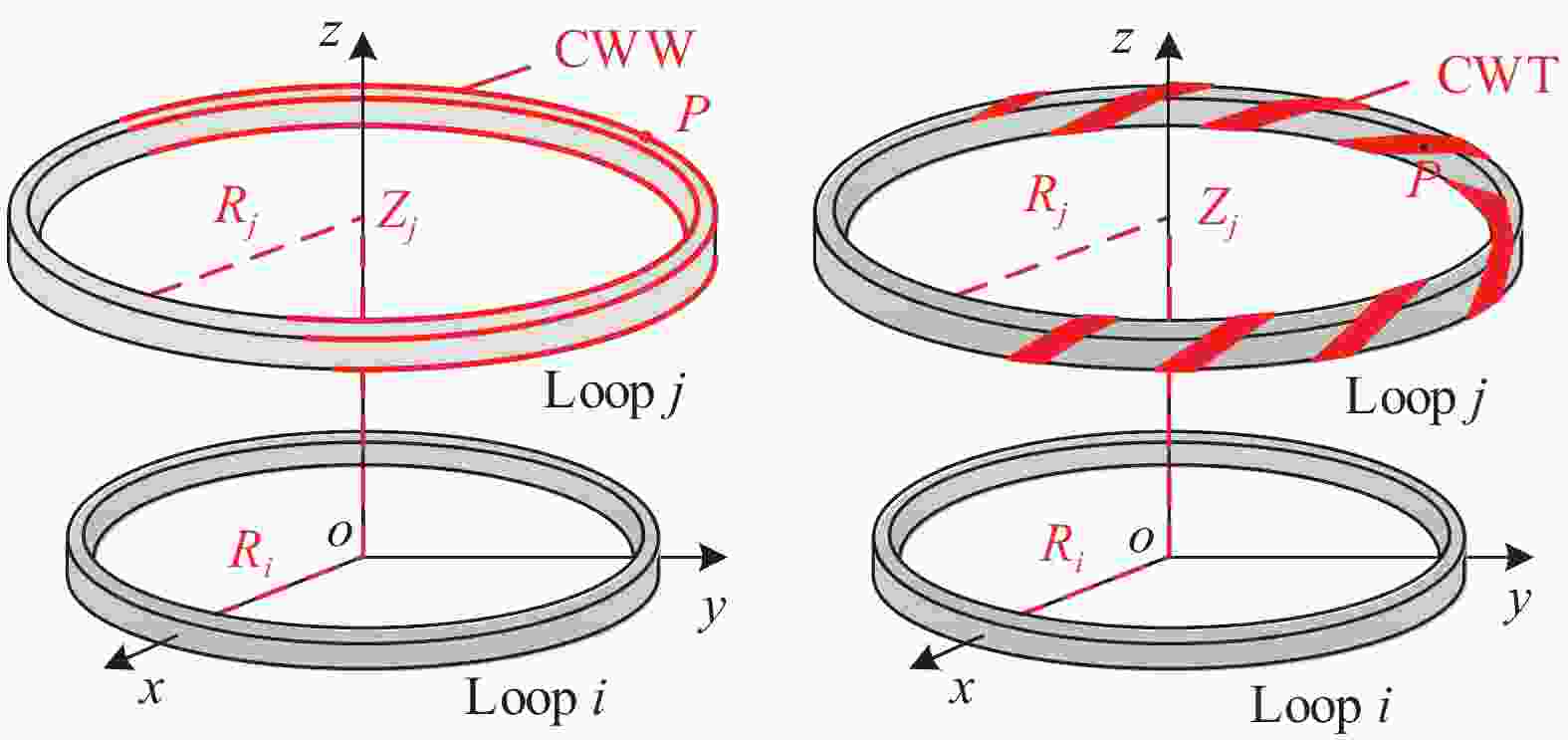
CWT的耦合电感与其包绕螺距相关，而CWW的耦合电感与其布线倒角位置相关。为尽可能减小同绕补偿线圈耦合电感与超导线圈耦合电感的差异，需要建立同绕补偿线圈耦合电感分析模型，并根据计算结果优化CWT的包绕螺距和CWW的布线位置以取得最佳补偿效果。以托卡马克极向场线圈为例，线圈可划分为若干个同轴且相互之间平行的圆形电流回路，CWW则同样划分为相互平行的圆形回路，而CWT则沿着圆环回路呈螺旋线结构，如图7所示。

Figure 7.  Mutual inductance calculation model for CWW and CWT

其中一电流圆环回路$ i $在另一圆环回路$ j $上任意一点$ P $处产生的环向磁矢势为^[29]：

式中：

$ {\mu }_{0} $ ——真空磁导率（H/m）；

$ I $ ——圆环回路$ i $中的电流（A）；

$ {R}_{i} $和$ {R}_{j} $ ——圆环回路$ i $和$ j $的半径（m）；

k ——$ \dfrac{4{R}_{i}{R}_{j}}{{\left({R}_{i}+{R}_{j}\right)}^{2}+{Z}^{2}} $；

$ Z $ ——圆环回路间轴向高度差（m）；

$ K\left(k\right) $和$ E\left(k\right) $ ——第一类和第二类完全椭圆积分，$ K\left(k\right)={\int }_{0}^{\tfrac{{\text{π}} }{2}}\dfrac{{\mathrm{d}}\varphi }{\sqrt{1-{k}^{2}{\mathrm{s}\mathrm{i}\mathrm{n}}^{2}\varphi }},E\left(k\right)={\int }_{0}^{\tfrac{{\text{π}} }{2}}\sqrt{1-{k}^{2}{\mathrm{s}\mathrm{i}\mathrm{n}}^{2}\varphi }{\mathrm{d}}\varphi $。

根据互感公式，利用上述磁矢势可计算圆环回路$ i $与圆环回路$ j $及其CWW和CWT间的耦合互感，如式（6）所示：

式中：

$ {{{\boldsymbol{A}}}_{ij}} $ ——圆环回路$ i $在圆环回路$ j $上产生的环向磁矢势（V·s/m），由式（5）给出。

基于式（6），分别选择圆环回路$ j $、CWW和CWT作为闭合积分路径，则可分别得到圆环回路$ i $与圆环回路$ j $及其CWW和CWT间的耦合互感。

利用上述模型，可计算线圈每一个圆环回路及其CWW和CWT与其余圆环回路间的电感，并在累加后得到整个线圈的电感。详细计算过程请参考文献[29]中的介绍，通过计算不同倒角处CWW和不同螺距CWT与线圈间互感，并与线圈自身电感进行比较，从而选出耦合电感差异最小的优化方案。以CFETR中心螺管模型线圈为例，其CWW和CWT的最优布线方案及其噪声抑制比如表2所示。

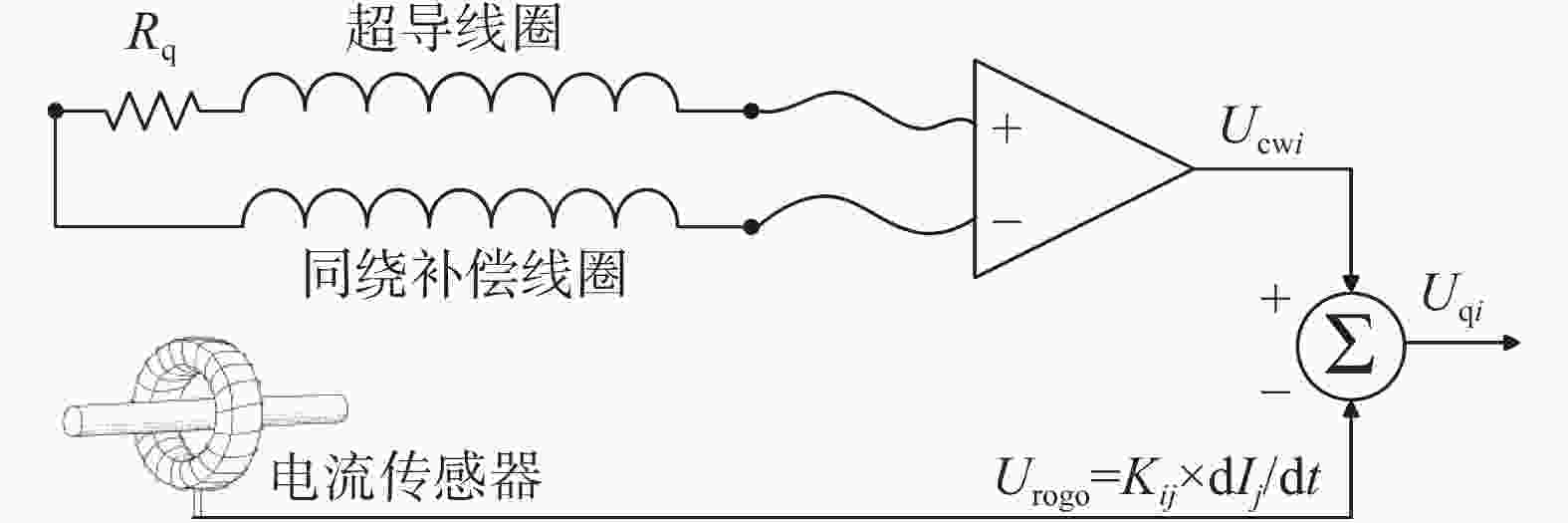
初级补偿可以抑制95%以上的感应电压干扰，但残余干扰仍无法满足失超电压探测信噪比的要求，需要通过二次补偿进一步降低干扰残余，避免造成失超探测的误判和误触发。如图8所示，对于线圈间耦合干扰，二次补偿利用罗柯传感器测量干扰源的电流变化率$ {{\mathrm{d}}I}_{j}/{\mathrm{d}}t $，并通过信号处理算法将其乘以相应补偿系数$ {K}_{ij} $后与初级补偿后的探测信号叠加，从而将噪声抑制比提高到99.9%以上，即：

Figure 8.  Secondary compensation for quench voltage detection

其中，补偿系数$ {K}_{ij} $为固定值，每轮实验前将各个线圈依次通入固定变化率的测试电流，以此来标定线圈间耦合干扰的固定补偿系数。

而对于等离子体耦合干扰，由于耦合互感受等离子体位形等时变参数的影响呈现动态特性，因此根据时变参数动态调整补偿系数是实现精准补偿的基础。特别是在等离子体电流爬升和下降过程中，等离子体与极向场线圈间耦合互感随等离子体位形和分布不同而变化。为了实现动态补偿需要根据位形变化实时反演等离子体耦合互感，为此将等离子体分布区域划分为$ a\times b $个网格，每个网格对应一个等离子体电流环，如图9所示。利用式（5）和式（6）可以分别计算每个等离子体电流环与极向场线圈间的耦合互感，由此可建立一个耦合系数矩阵，再根据等离子体位形识别不同时刻的有效等离子体电流环及其对应的耦合系数矩阵元素，即可快速实现不同位形下等离子体耦合互感的反演计算。

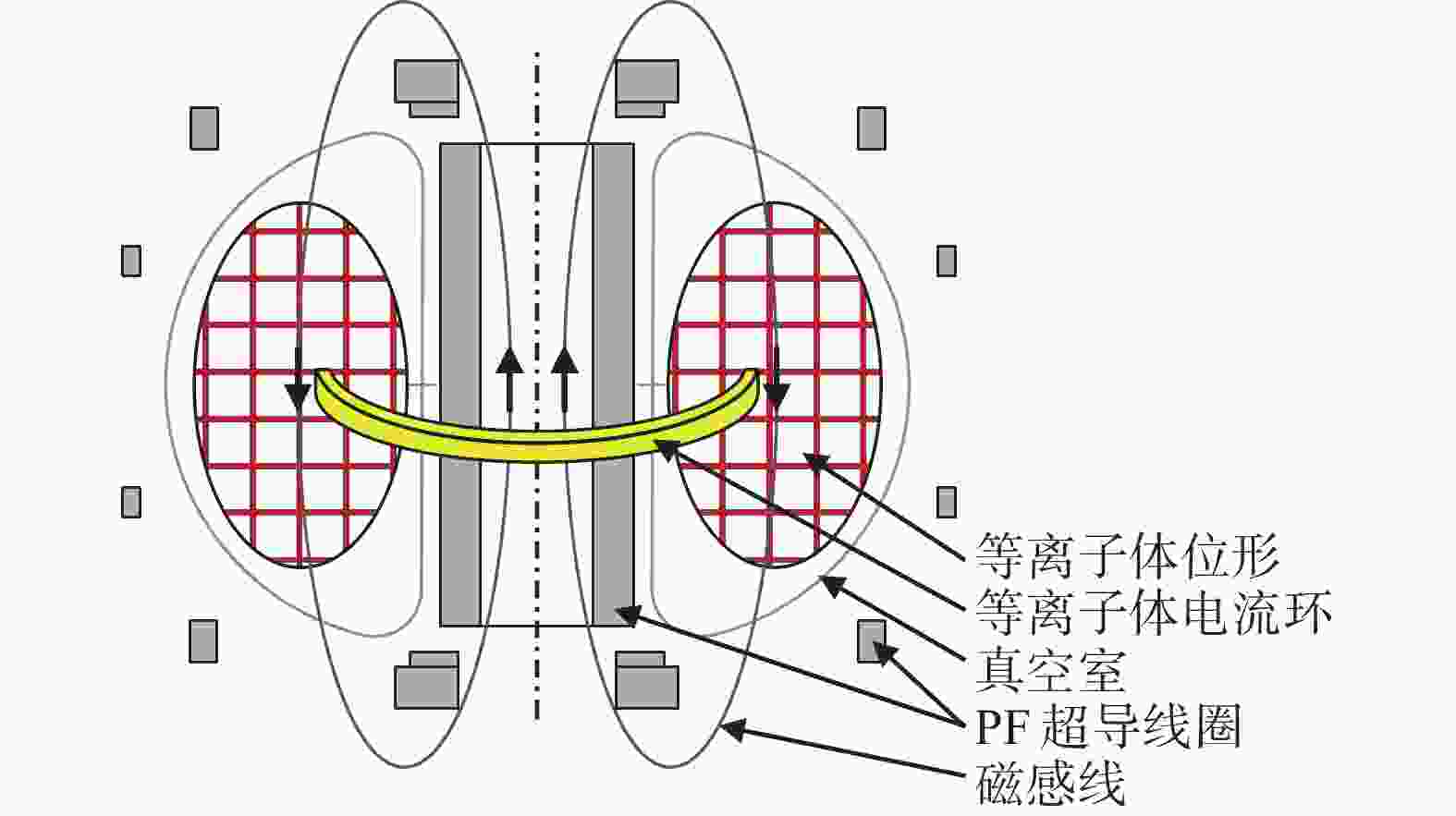
Figure 9.  Meshing of plasma distribution area and schematic diagram of effective plasma current loop

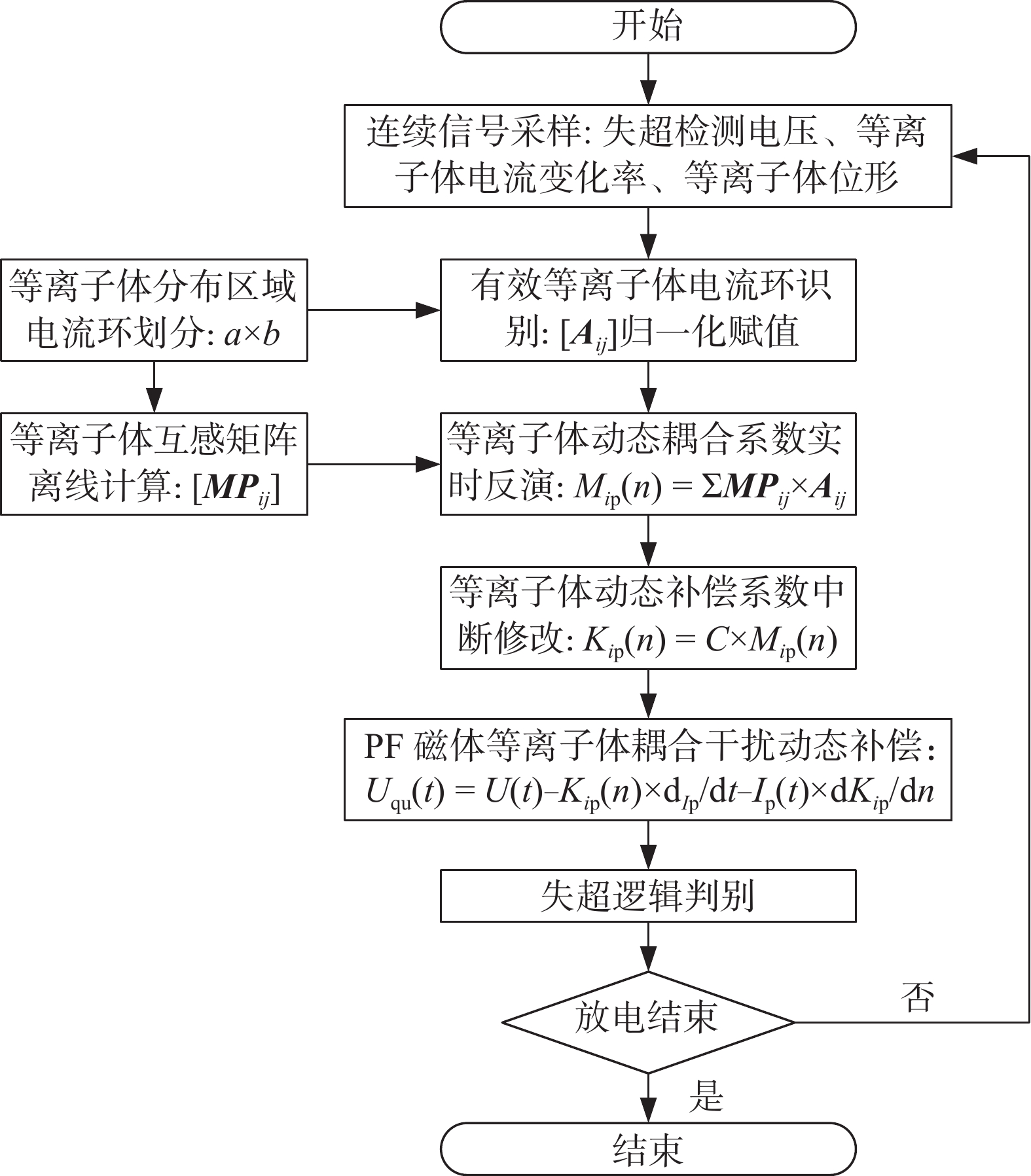
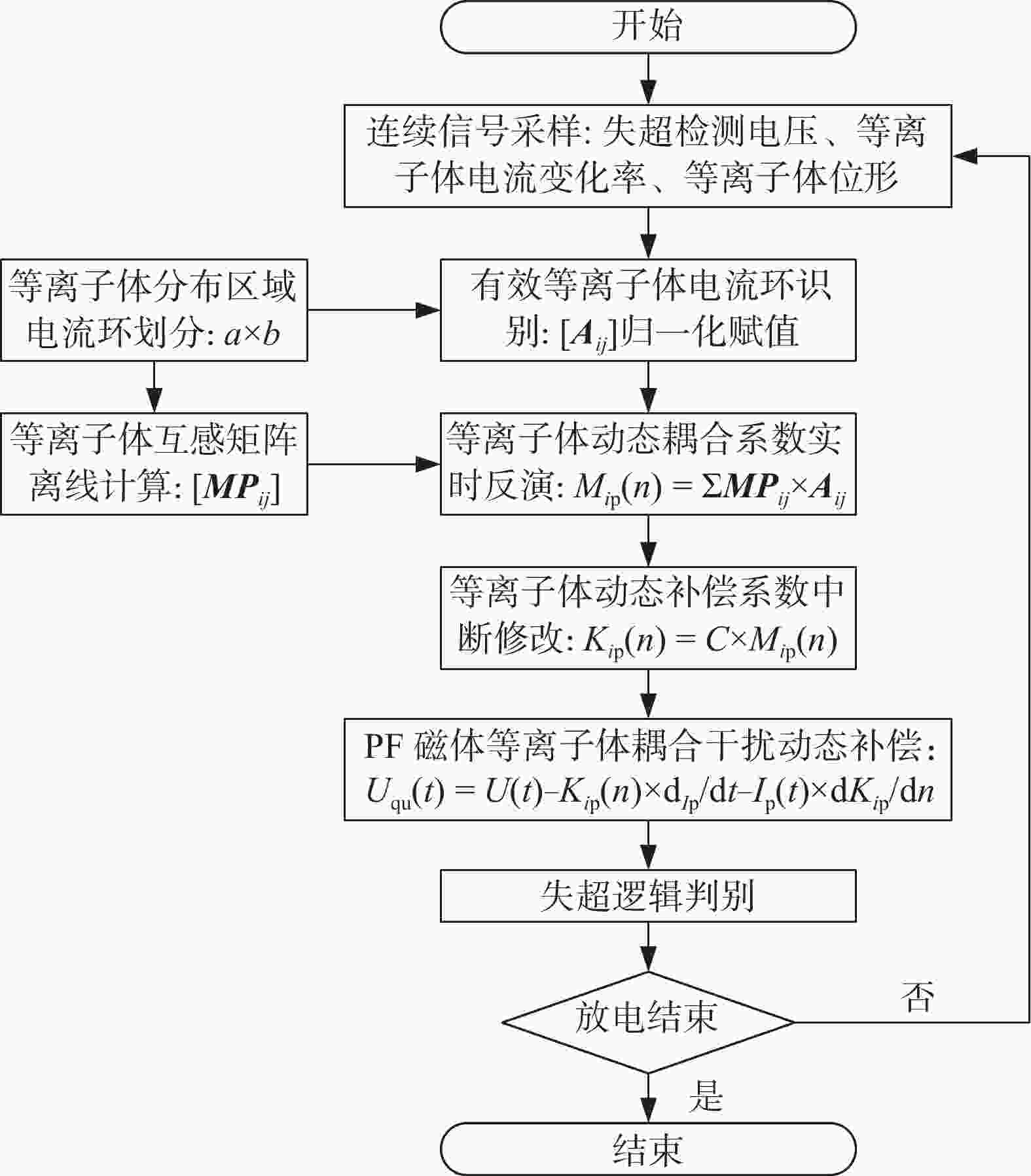
动态补偿流程如图10所示，为满足实时性要求，动态补偿采用离线计算与实时反演相结合策略^[30]：首先，将等离子体分布区域划分为若干个电流环，并离线计算每个电流环与极向场线圈间的耦合互感，以此建立耦合互感矩阵$ \left[{{\boldsymbol{MP}}}_{ij}\right] $；其次，根据实时等离子体位形识别有效电流环，并建立权重系数矩阵$ \left[{{\boldsymbol{A}}}_{ij}\right] $，将有效电流环对应元素进行归一化赋值，其余元素则赋值为零；然后，将系数矩阵和互感矩阵对应元素相乘并累加$ M_{\mathrm{\mathit{i}p}}\left(n\right)=\sum{{\boldsymbol{MP}}}_{ij}\times\boldsymbol{A}_{ij} $，以实时反演计算等离子体动态耦合互感；最后，将动态耦合互感转化为相应的动态补偿系数$ K_{\mathrm{\mathit{i}p}}\left(n\right)=C\times M_{\mathrm{\mathit{i}p}}\left(n\right) $，并通过中断机制实时修改以实现动态精准补偿。

Figure 10.  Dynamic compensation process of plasma-coupling interferences

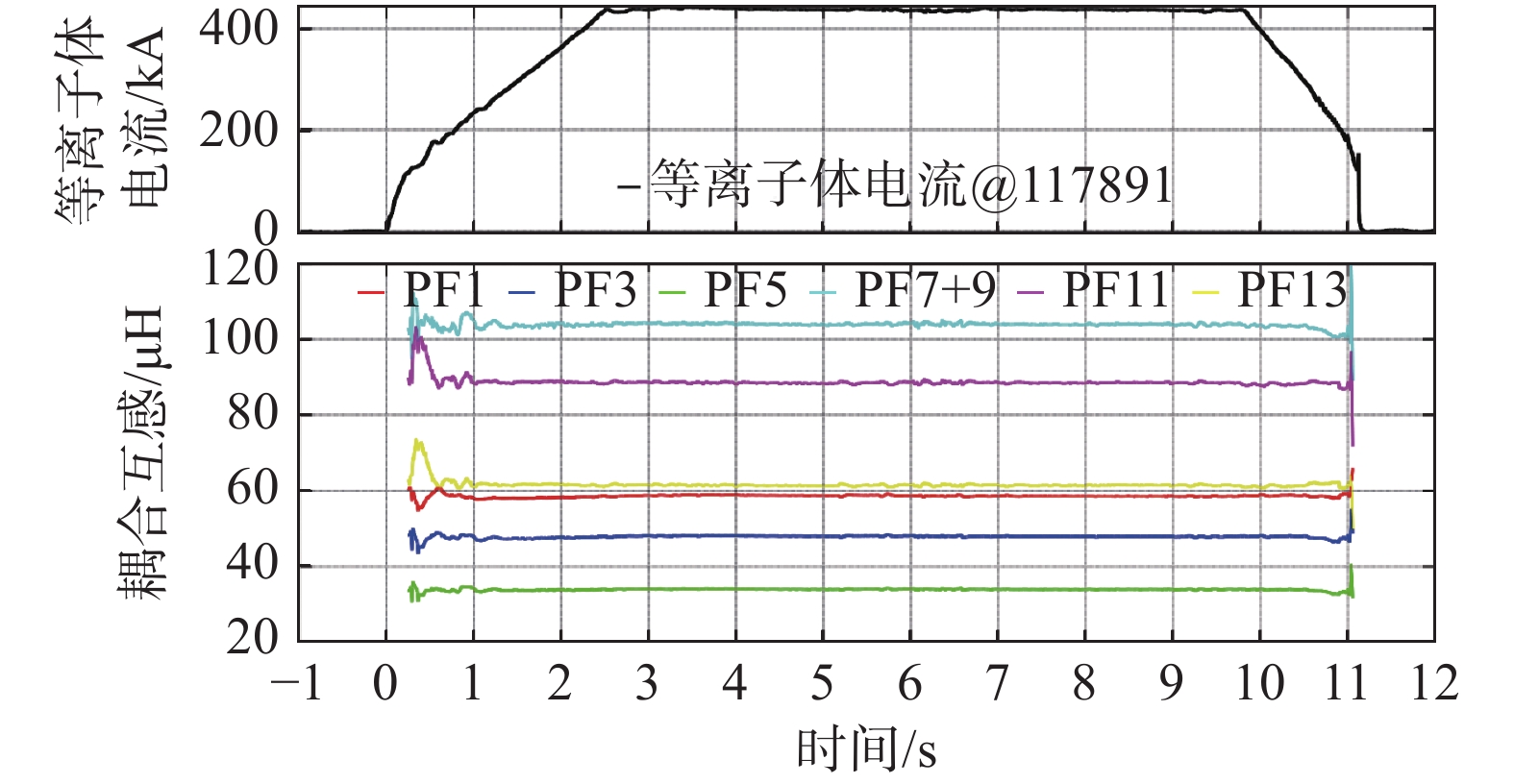
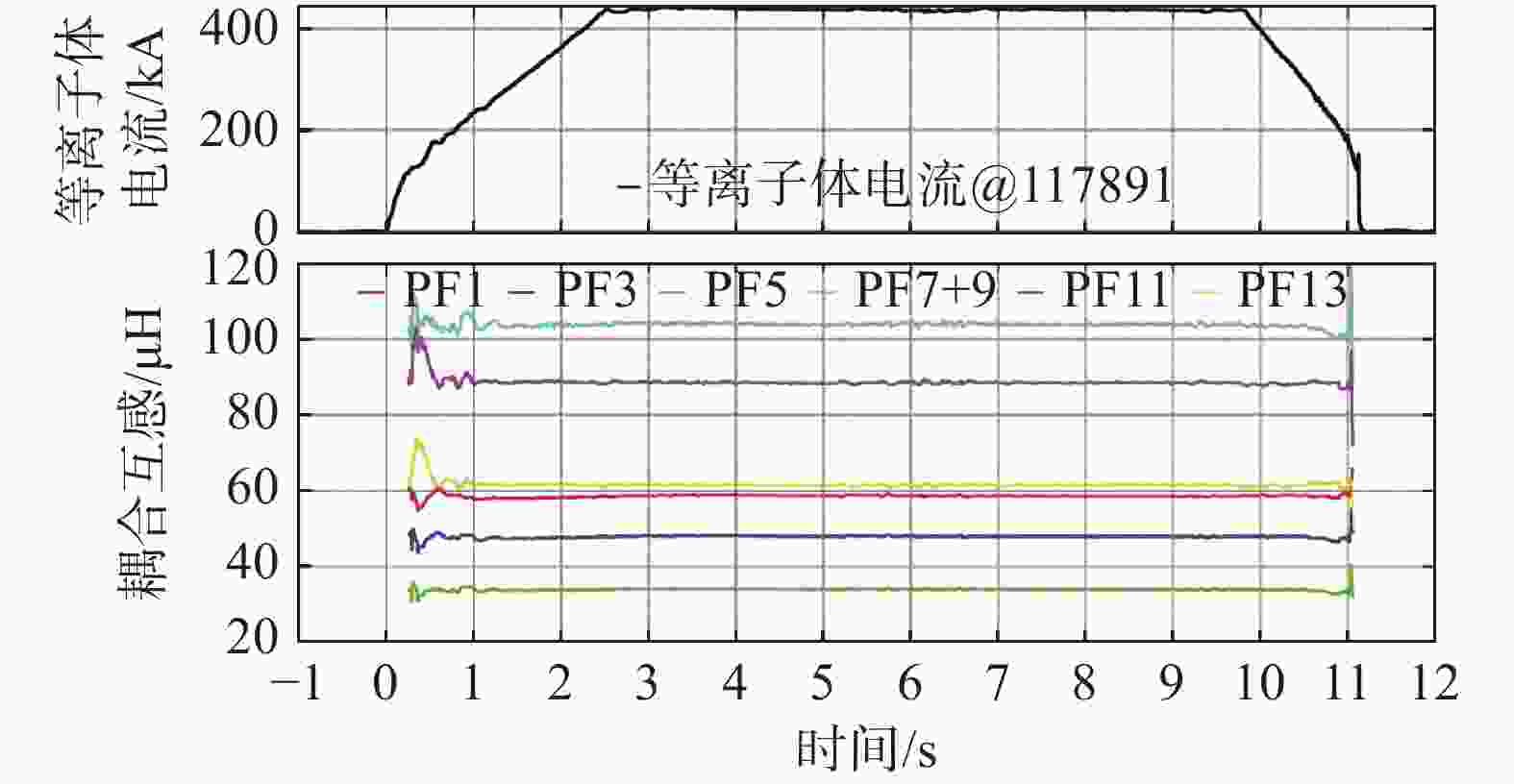
根据上述补偿方案，动态反演结果表明EAST装置的等离子体与不同极向场线圈间耦合互感为30～110 μH，如图11所示。由于EAST的偶数编号极向场线圈与奇数编号极向场线圈关于中平面对称，图11仅展示了等离子体与PF1、PF3、PF5、PF7+9、PF11和PF13线圈间的动态耦合互感变化曲线（其中7号线圈与9号线圈串联供电），并给出等离子体电流变化曲线以直观展示在等离子体放电不同阶段的动态耦合互感变化趋势。

Figure 11.  Inversion results of dynamic coupling coefficients between plasma and EAST CS & PF coils

在等离子体电流平顶段，由于等离子体位形和分布相对固定，此时等离子体与极向场线圈间耦合互感相对固定。可以看到，随着中心螺管线圈逐渐远离装置中平面，导致PF1、PF3和PF5线圈与等离子体间耦合互感也有减小趋势；由于极向场大线圈匝数差异较大，导致PF11和PF13线圈与等离子体间耦合互感差异较大；偏滤器线圈匝数最多，因而与等离子体耦合最强，所以PF7+9线圈与等离子体间耦合互感最大达到104 μH。而在等离子体电流上升和下降阶段，耦合互感受时变位形影响变化明显，相对于平顶段稳定值，最大变化范围为±17%，由此可见动态补偿的必要性。

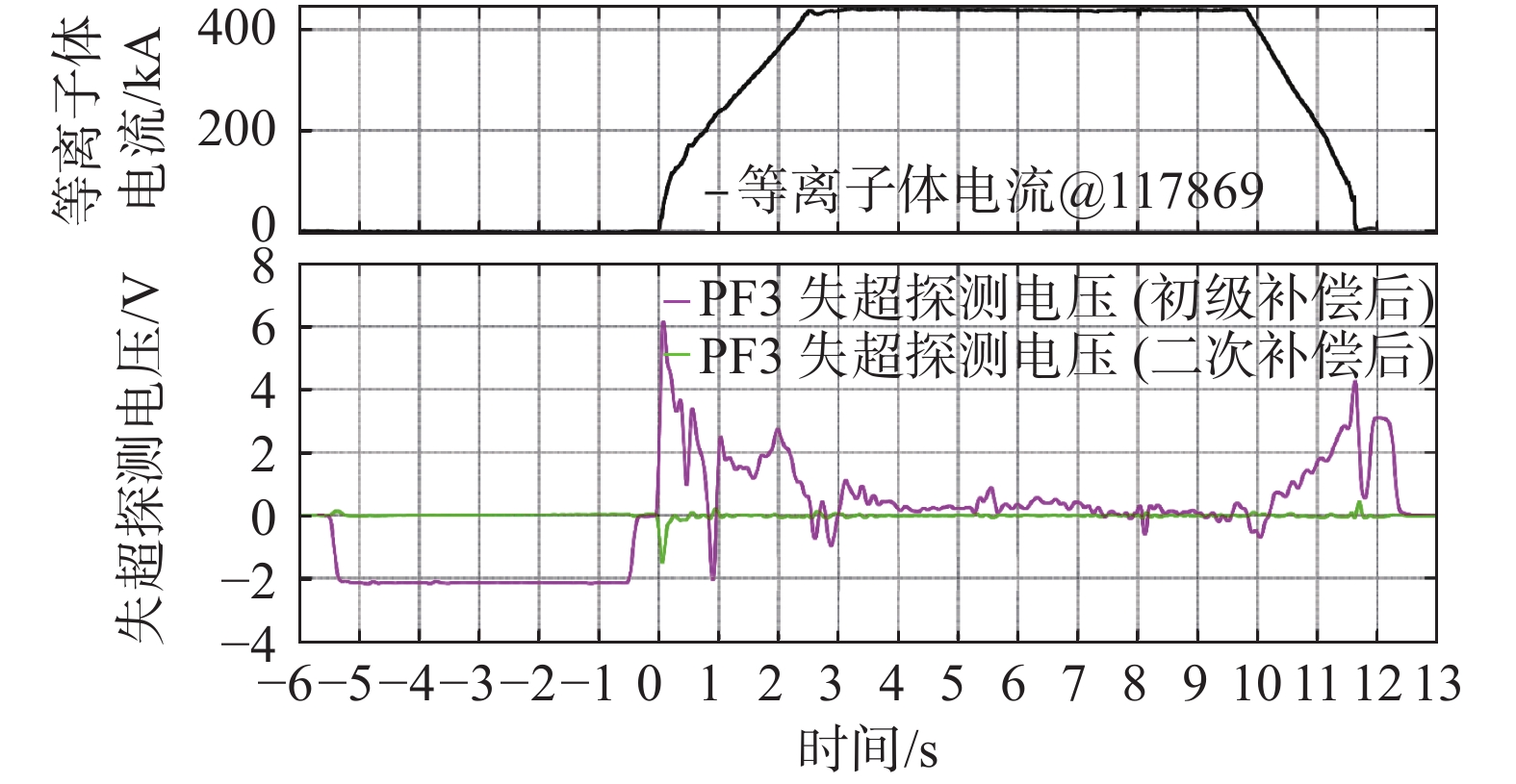
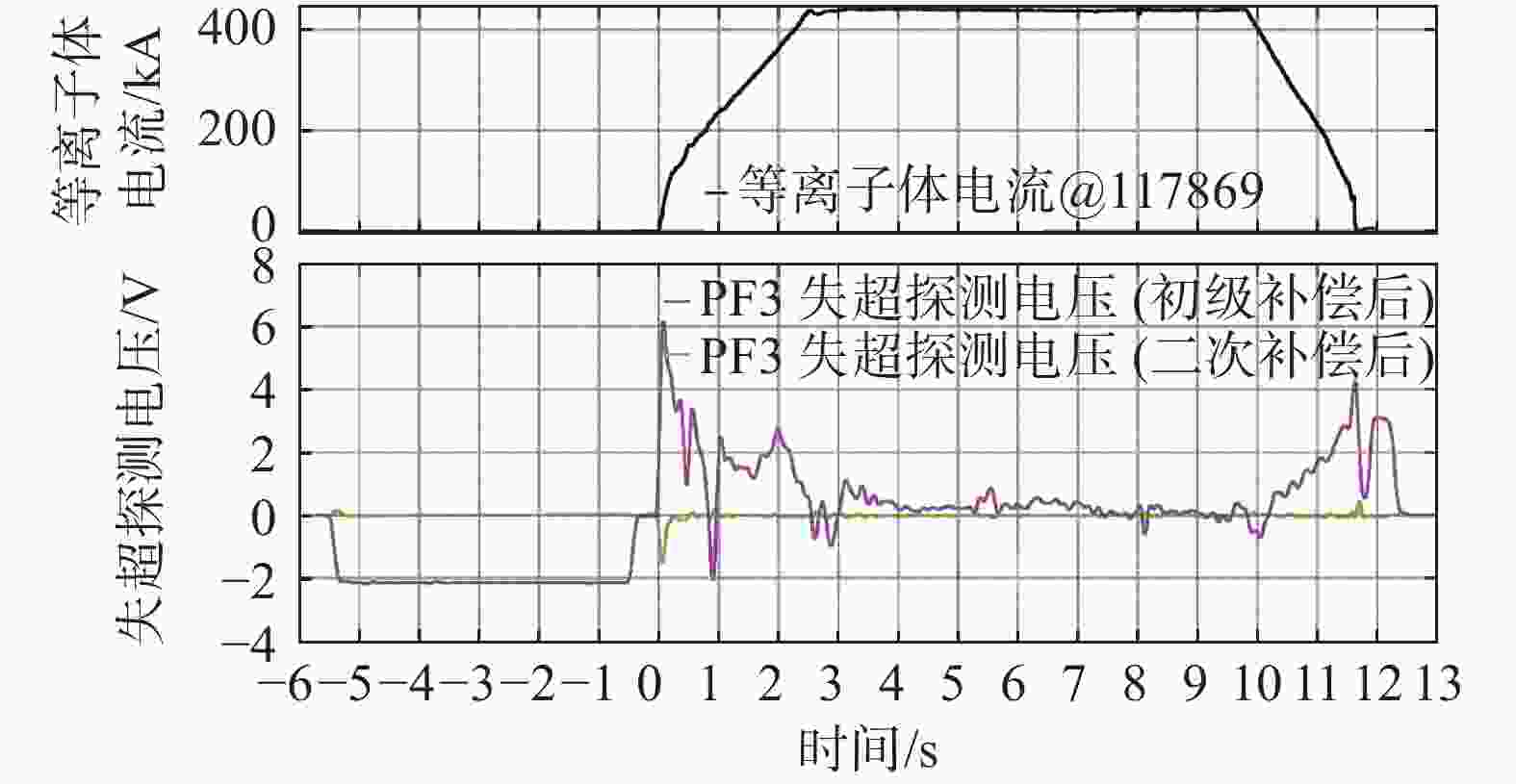
以EAST中心螺管线圈PF3为例，对比了初级补偿后和二次补偿后的失超探测电压信号，同样给出等离子体电流变化曲线以直观展示等离子体放电前后的残余干扰及补偿效果，如图12所示。在等离子体击穿（零时刻）前中心螺管线圈和极向场线圈运行电流以固定速率同向爬升，由于磁体间是强耦合，尽管经过初级补偿，残余干扰电压仍超过2 V，远远无法满足失超探测信噪比要求，而经过二次补偿后干扰残余被抑制到20 mV以下。在等离子体建立、爬升和下降阶段，极向场线圈运行电流则根据等离子体约束需要进行反馈控制，加之等离子体耦合干扰，初级补偿后残余干扰电压仍可超过5 V且变化无序，而经过二次补偿特别是等离子体耦合干扰动态补偿后平均干扰残余可被抑制到50 mV以下。因此，二次补偿可以抑制99%以上的干扰残余，两级补偿后可以实现噪声抑制比大于99.95%，避免耦合干扰造成失超探测的误判和误触发。考虑到不同极向场线圈的失超探测电压阈值为500～1 000 mV，从而满足失超探测的信噪比大于10的要求，保证失超探测的可靠性。

Figure 12.  Comparison of the voltage with primary compensation and the voltage with secondary compensation for EAST PF3 quench detection

及时、可靠的失超探测是超导磁体运行安全的关键所在，享有托卡马克装置安全的最高等级。聚变磁体以失超电压探测作为主方案，并通过失超分析合理选择判别阈值，保证磁体运行安全。托卡马克复杂电磁环境对失超电压探测产生耦合干扰，为此失超电压探测采用两级补偿方案实现预期噪声抑制比。初级补偿采用同绕补偿线圈方案，通过互感计算分析以优化同绕带和同绕线布线方案，能够实现 > 95%的噪声抑制比。二次补偿通过信号处理单元对磁体间耦合干扰和等离子体耦合干扰分别进行解耦补偿和动态补偿，特别是动态补偿能够根据等离子体位形的变化实现对补偿系数动态调整，有效提高了对等离子体耦合干扰的补偿精度，进而实现综合噪声抑制比 > 99.9%。实测EAST失超探测电压经过两级补偿后平均干扰残余 < 50 mV，满足失超探测信噪比 > 10要求，保证失超探测可靠性。同时，建立的同绕补偿线圈优化分析模型和等离子体耦合干扰动态补偿机制可拓展至其他托卡马克装置，从而为未来聚变堆的失超探测设计和磁体安全运行提供强有力的支持。