Static Calculation on Integrated System of Offshore Wind Turbine Foundation and Aquaculture Cage

海上风能发电需要较大面积的海域来满足该行业的海上活动，随着工程技术的成熟，风电场使用海域逐渐扩大，海域使用矛盾也越来越严重^[1]。海上风电场使用海域逐渐扩大，和海洋渔业养殖发展不可避免地产生资源冲突，包括海域使用矛盾、劳动力争夺、经济资源竞争等。海上风机的存在阻碍渔船的航行，风场限制渔船穿梭，建造期间风场范围内禁止捕捞作业，运营阶段根据风场管理要求对捕捞也有一定的限制，海上风电场的建设对渔业和依赖渔业的沿海地区发展会产生一系列直接和间接的负面影响^[2]。据相关预测，2050年世界人口将接近90亿。随着人口的增长，海鲜的需求也在稳步增加。自然渔业资源获取有限，越来越多的海洋生物需求必须通过水产养殖来满足。为了解决海上风电场与海洋渔业养殖的冲突，各行业利益相关者提出了多元化海域使用的设想，整合海上风电场与海洋渔业养殖，最大限度利用海洋空间。有研究表明^[3-5]，海洋水产养殖系统的进一步发展和改造将直接依赖于风电场的发展，因此，未来海上风机技术的研究和水产养殖系统的发展相辅相成。

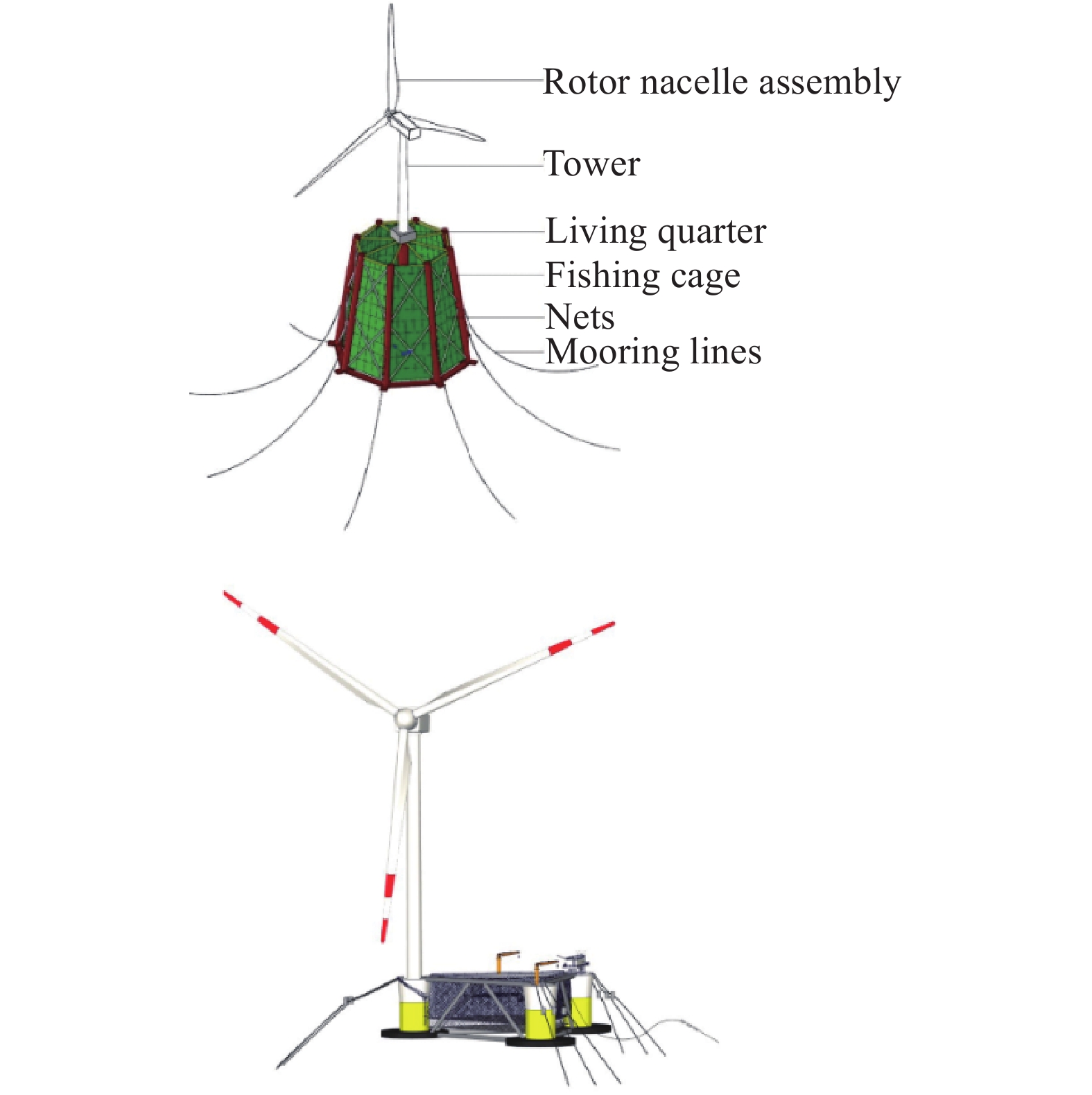
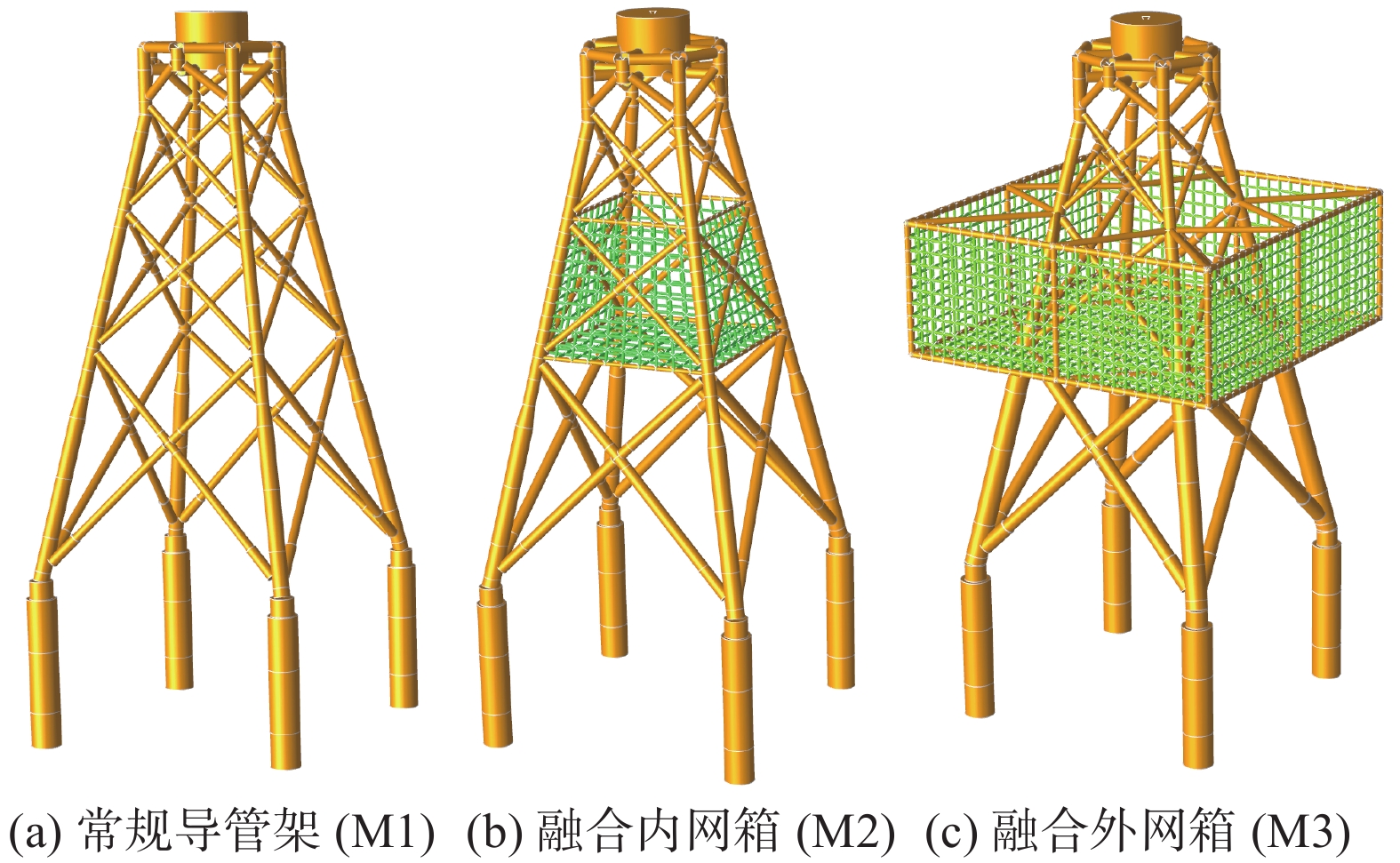
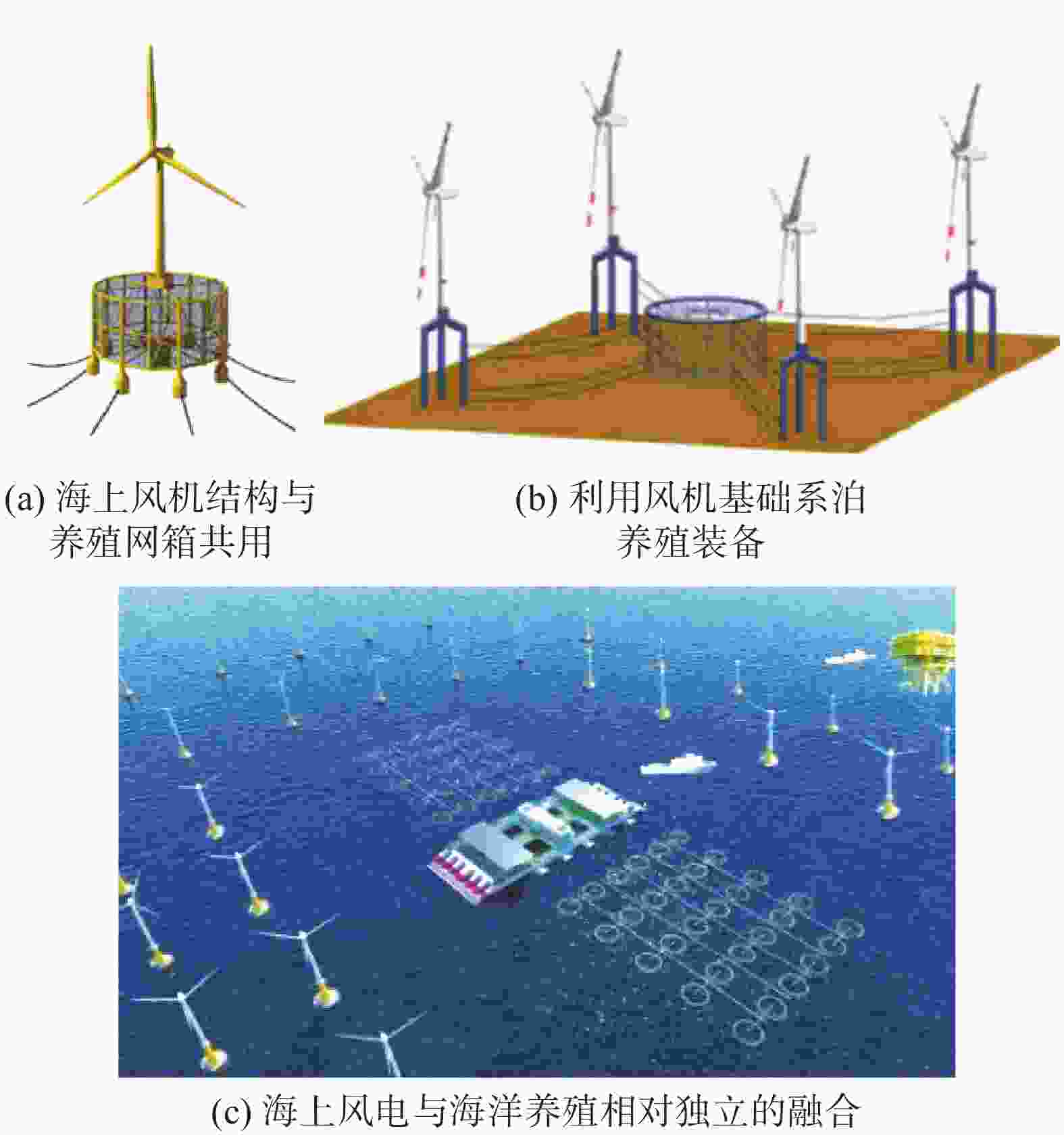
海上风电与渔业养殖融合方式主要分为3种^[6-7]：（1）海上风电与人工鱼礁融合，此融合方式兼顾海洋生态修复和增殖放流；（2）海上风电与贝藻类养殖融合，主要用于贝类、藻类的养殖；（3）海上风电与养殖网箱融合，主要用于鱼类的养殖。目前，应用较多的是海上风电+养殖网箱的融合方式。此融合方式主要设计思路是如何将水产养殖设备（如网箱）连接到风机基础，如何将养殖网箱安装在海上风机之间的自由区域。海上风电与海洋养殖融合的模式根据风机与养殖装备的交互程度可分为3类^[3]：（1）风电机组与养殖装备结构共用的模式，如图1（a）所示；（2）利用风机基础系泊养殖装备的模式，如图1（b）所示；（3）海上风电仅给养殖网箱供电，海上风电与海洋养殖相对独立的融合发展模式，如图1（c）所示。

Figure 1.  Pattern of integration of offshore wind power and aquaculture cage

开发海上风电场用于水产养殖的“多用途”功能有助于进一步加强环境保护和扩大可持续水产养殖，已有不少资料从生物、技术、经济和社会与政策等方面探讨海上风电场-海水养殖互动多用途概念的开发可行性^[5]，并在北海地区开展了Butendiek和Nordergründe 1两个试验项目^[3]。由于政策支持和行业关注，如何将海上风电场与海洋牧场更好的融合成为时下探讨的热门话题，并涌现了各种形状和配置的风机基础加网箱的概念设计^[8-9]。然而，海上风机基础结构的开发和设计非常复杂，现阶段的风机基础加网箱的融合设计并未进行严格的评估，在建造和投入使用之前都缺乏验证。

各国海上风电场的渔业养殖仍处于实验研究阶段^[10]，一些学者根据单桩基础的特点，增加了养殖网箱设计，并研究融合结构的特性。Wang等^[11]提出固定式单桩风机与圆形网箱结合的结构，通过数值模型分析网箱对波浪传播的阻塞效应，研究非线性波与组合结构之间的相互作用。Zhang等^[12]设计海上风机单桩基础与钢制养殖网箱一体化结构，建立一体化结构在地震、风、波浪载荷作用下的动力特性和耦合机制，讨论不同减振器的影响，并对结构减振提出建议。Li等^[13]设计了1种导管架风机基础与养殖网箱相结合的一体化结构，并对该结构进行建模和动力分析，为工程应用提供了一定的参考。林旻等^[14]根据导管架风机基础构建养殖网箱，考虑波流入射角、网箱布设深度和生物附着程度的影响，分析极端波流条件下网箱系泊绳张力的变化，进一步评估导管架基础的结构安全性。

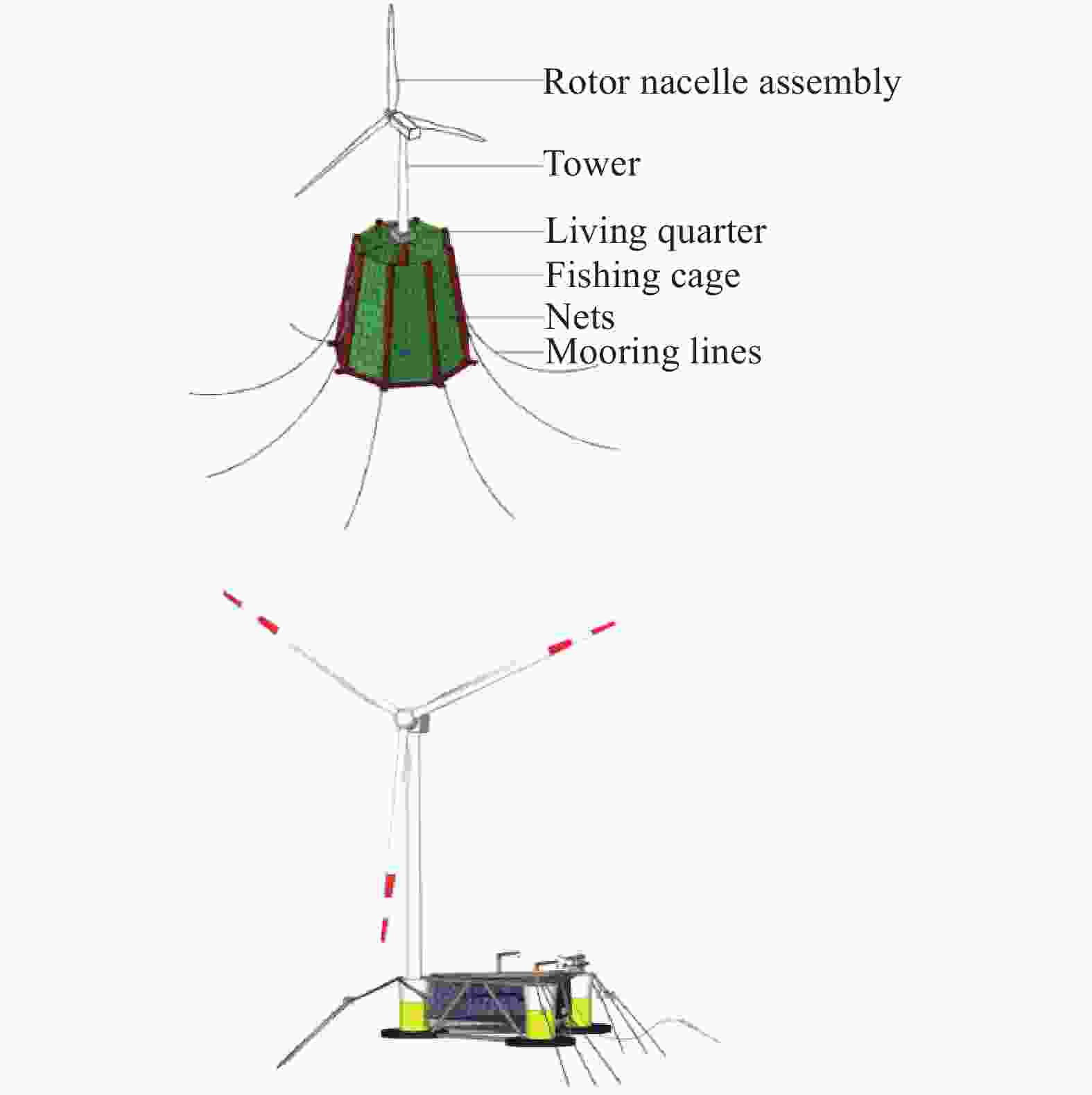
除了固定式海洋风机基础与养殖网箱相结合的设计，清华大学深圳国际研究生院海洋工程研究院对浮式风机与钢制网箱结合的设计进行了一定的研究并取得了可观的成果。该研究院的Zhang和Lei^[15]在2018年提出了将浮式风机与钢制网箱结合的概念，并通过数值模拟分析该设计的水动力性能。然而，分析过程进行了一定的简化，未考虑网衣的拖曳力影响和采用准静态方法进行系泊分析都在一定程度上影响了结果的准确性。为此，该研究院于2021年，对该设计进行了缩尺比为1∶30的模型试验研究^[16]，验证其拥有优异的耐波性和水动力性能，并根据试验数据调整OrcaFlex建立的数值模型^[17]，提高模型的精度。随后，该研究院改变网箱形状设计了新的浮式风机与网箱结合的结构，对该结构进行了缩尺比为1∶40的模型试验，试验数据与内部全耦合仿真工具的数值预测值获得良好的一致性，证实了所开发的数值模拟工具的准确性^[18]。其他科研单位也就漂浮式风机与养殖网箱结合做了一些研究。Zhang等^[19]设计了与NREL 5 MW漂浮式风机相匹配的钢制养殖网箱并与风机组成集成结构，通过FAST和AQWA软件建立该结构完全耦合的气动-液动-弹性-伺服-系泊动力学模型，证明该集成结构拥有良好的水动力性能，但未对结构强度进行校核。Cao等^[20]设计了带网箱结构的新型半潜式浮式风机，基于Froude数相似性要求设计了缩尺比为1∶40的模型试验，探究有网和无网的新型风机结构在不规则波浪以及风浪组合作用下的运动响应。Chu和Wang^[21]提出了1种Spar式漂浮式风机与养殖网箱的组合结构，并对该组合结构进行了水动力响应分析^[22]验证该结构比常规半潜式养殖网箱更稳定、系泊张力更小，同时设计了组合网箱的屏障结构^[23-24]。图2展示了结构各异的漂浮式风机加网箱设计。

Figure 2.  Offshore system integrating a floating offshore wind turbine with a fish cage

深海养殖网箱主要包括主体结构、网衣和系泊系统3个组成部分，针对网箱的研究集中在这些组成部分的开发和评估。网箱的计算涉及复杂的载荷非线性、几何非线性、材料非线性问题，受到水流的影响会发生较大位移和变形。在工程应用中，网箱可能存在初始应力集中、网格尺寸发生改变、网绳连接有缺陷等问题，传统网衣材料刚度非常低，很难精确定义初始长度和刚度^[25]。唐鸣夫^[26]在网目群化的基础上提出了十字单元水动力分析法，推导出了网结构水动力与网结构密实度、雷诺数、结构水下投影面积及水流冲击角的关系。生物污垢通常会导致网堵塞并降低网箱内的水交换率和氧气供应，放大网箱上的波浪载荷增加结构失效的风险，并影响鱼类的健康^[27]。为了减少计算量，方便实际工程应用与计算，文章提出1种新的网箱等效方法用于网衣水动力模拟计算方法，等效模型中网衣和纲绳简化为管单元，模型简化前后遵循网衣（包含纲绳）质量相等，网衣（包含纲绳）附加海生物质量相等，网衣（包含纲绳）水动力性能相等的要求。

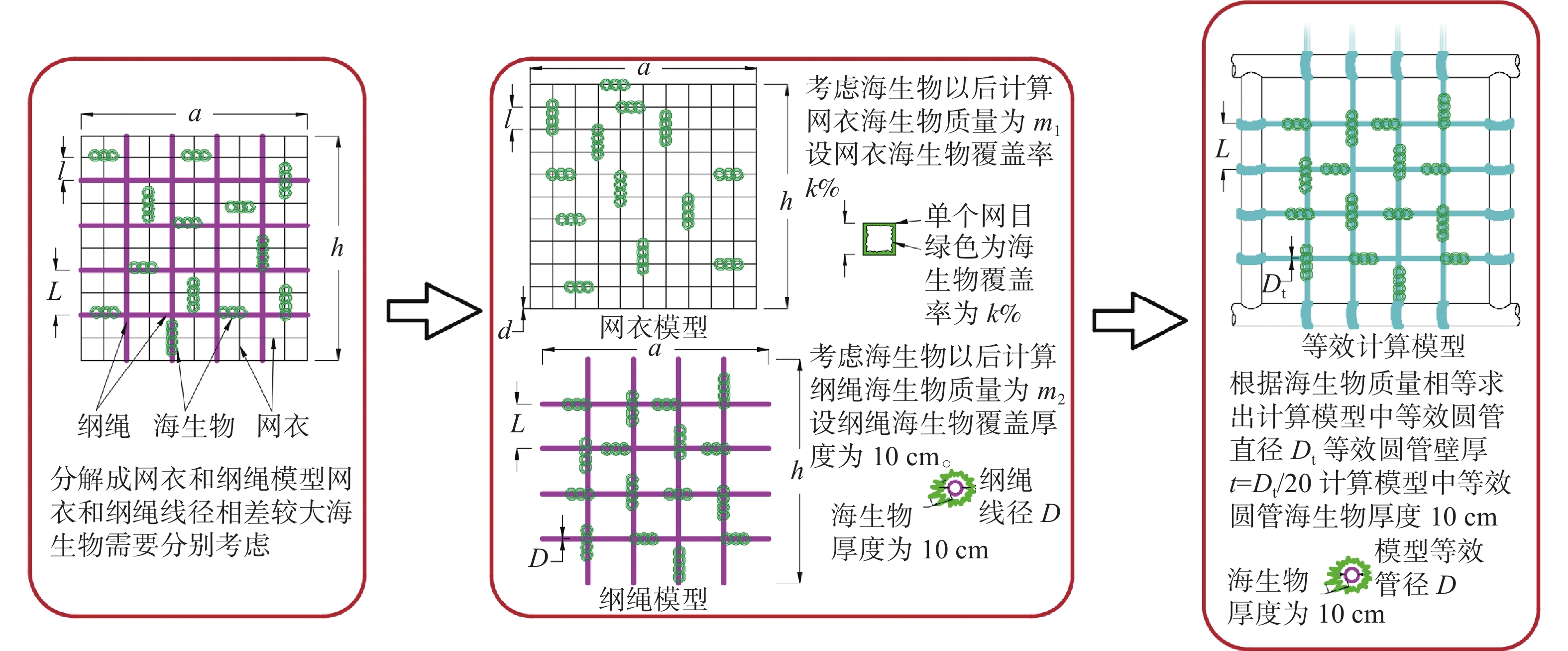
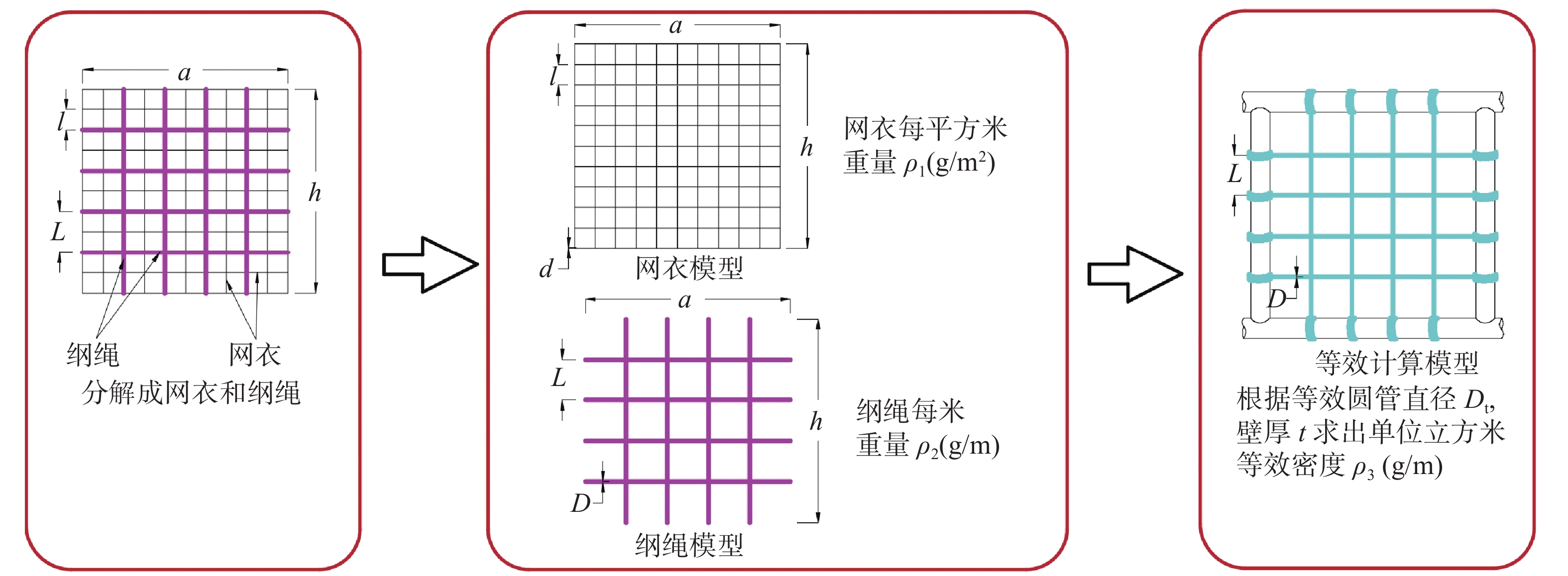
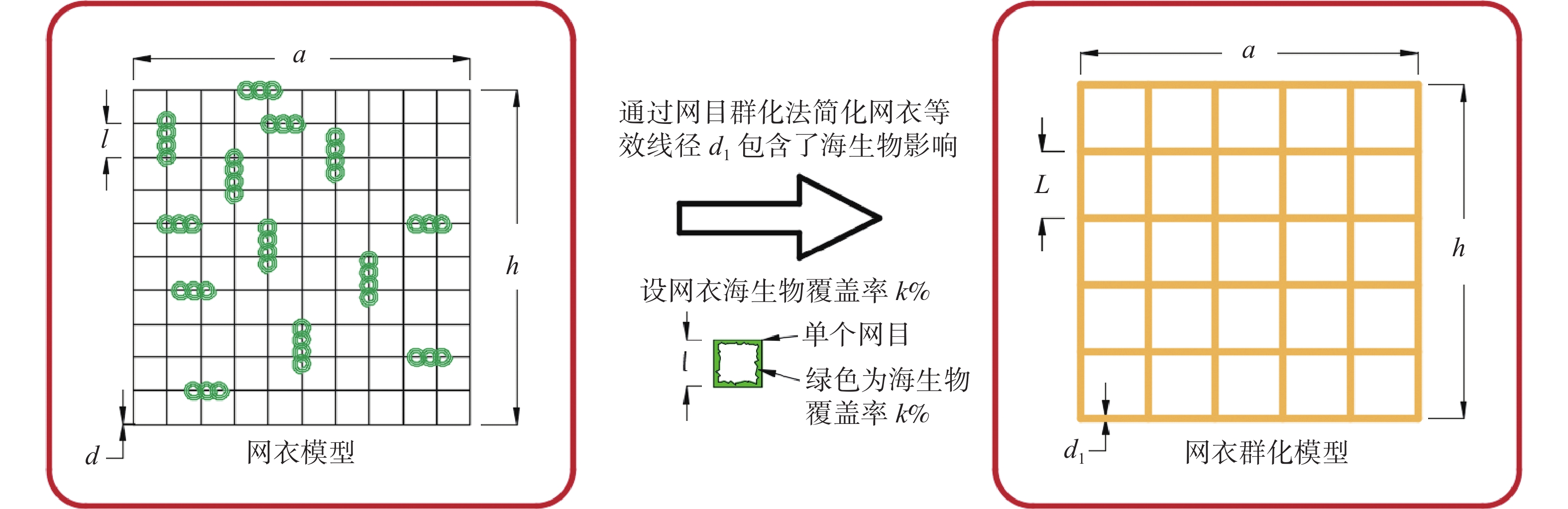
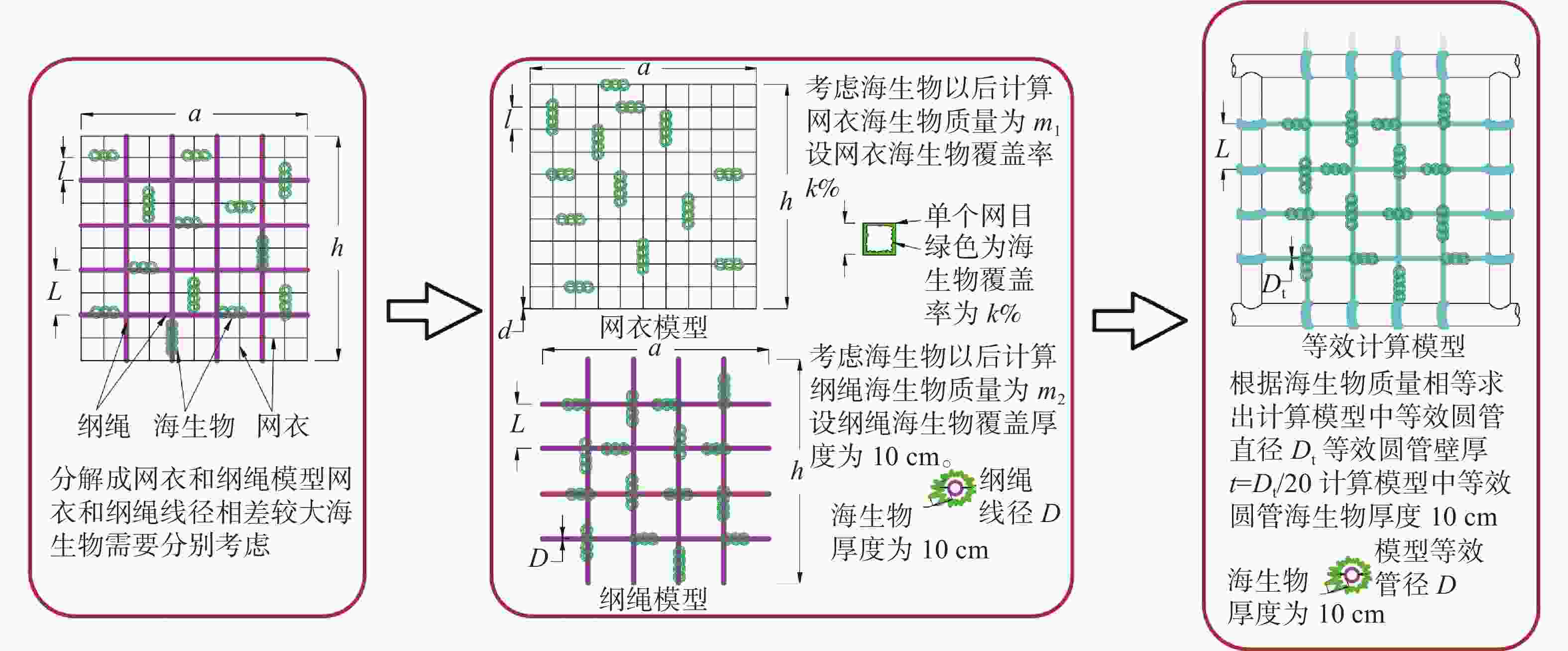
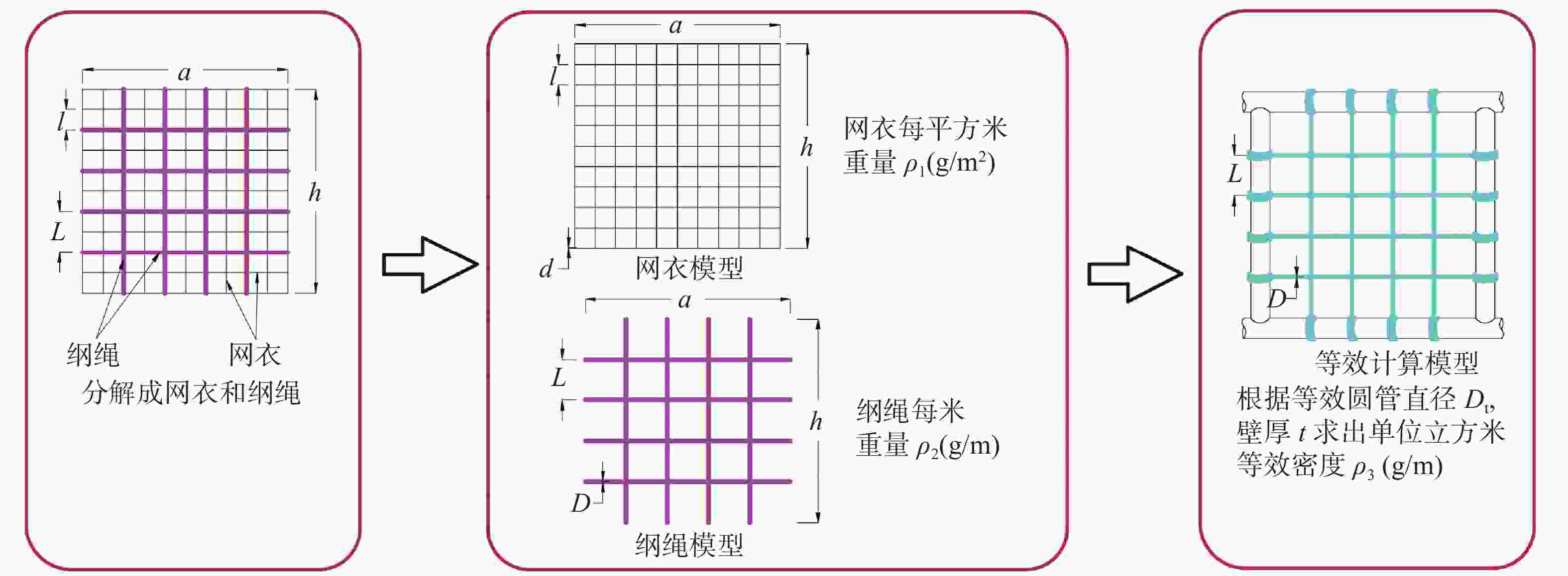
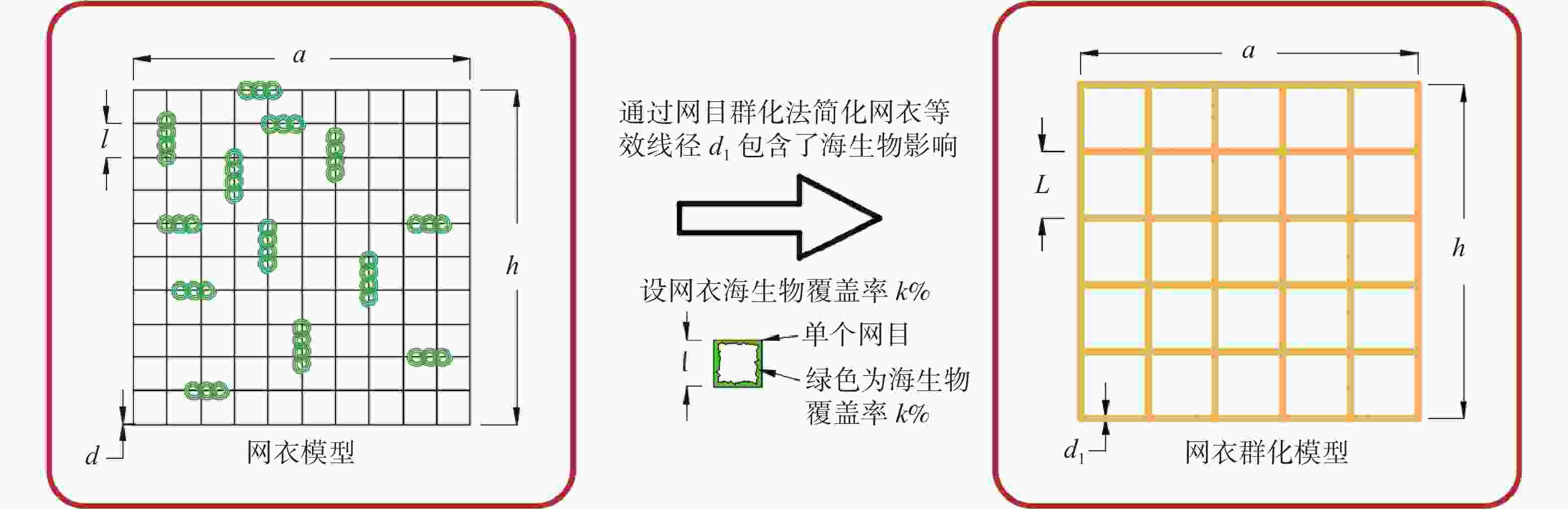
网衣和纲绳的网目不同，因此，需要将网衣和纲绳的海生物分别考虑，网衣网目尺寸较小，因此，可以假定海生物覆盖百分比来考虑，纲绳线径较粗并且网目较大，海生物可以按照增加厚度来考虑。设网衣海生物覆盖率为$ P = k\% $，则网衣海生物质量计算可按图3计算。建模计算过程中，网衣和纲绳质量要保持一致，其等效过程如图4所示。

Figure 3.  Step 1: Mass equivalent of marine growth

Figure 4.  Step 2: Mass equivalent of net cage

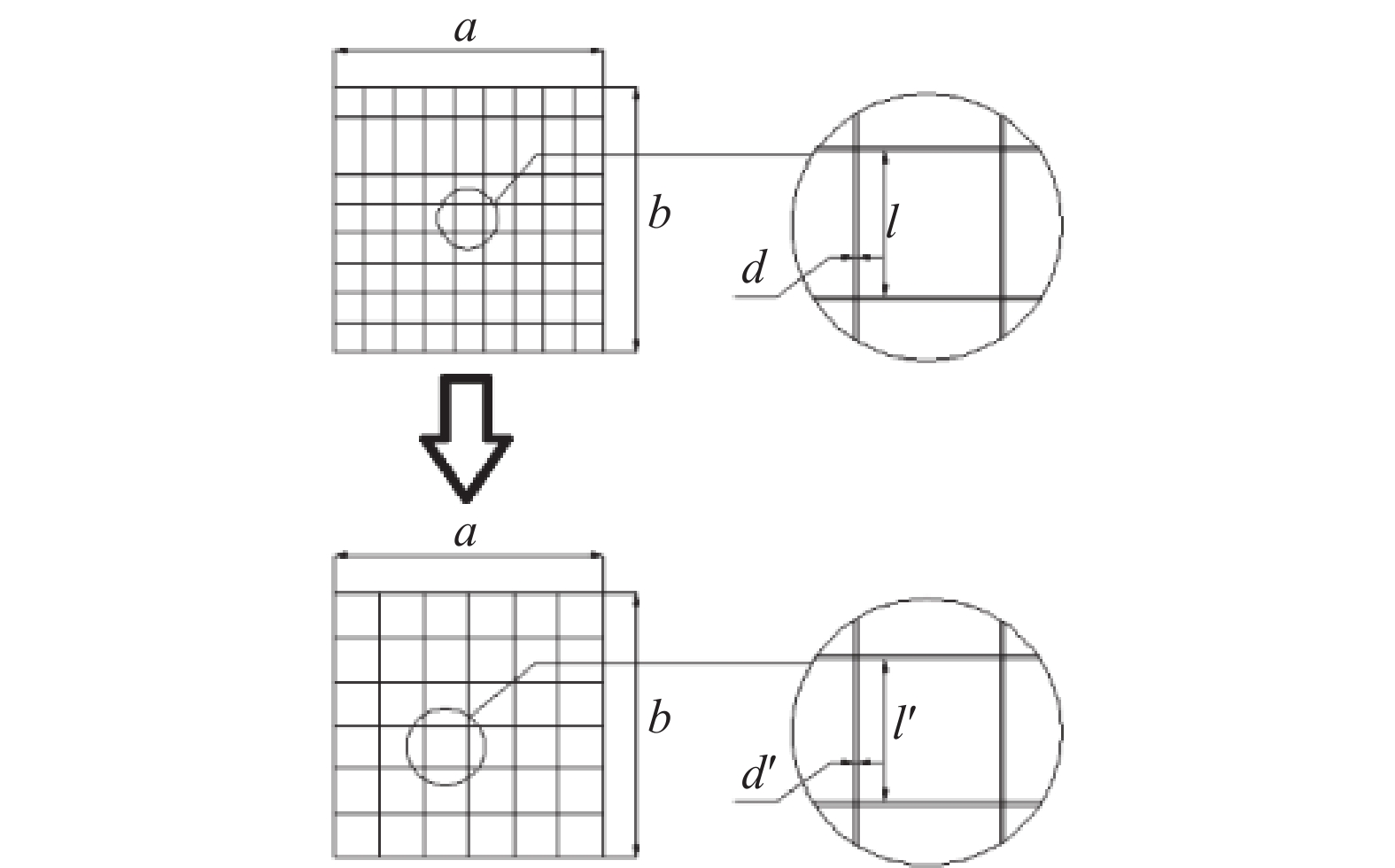
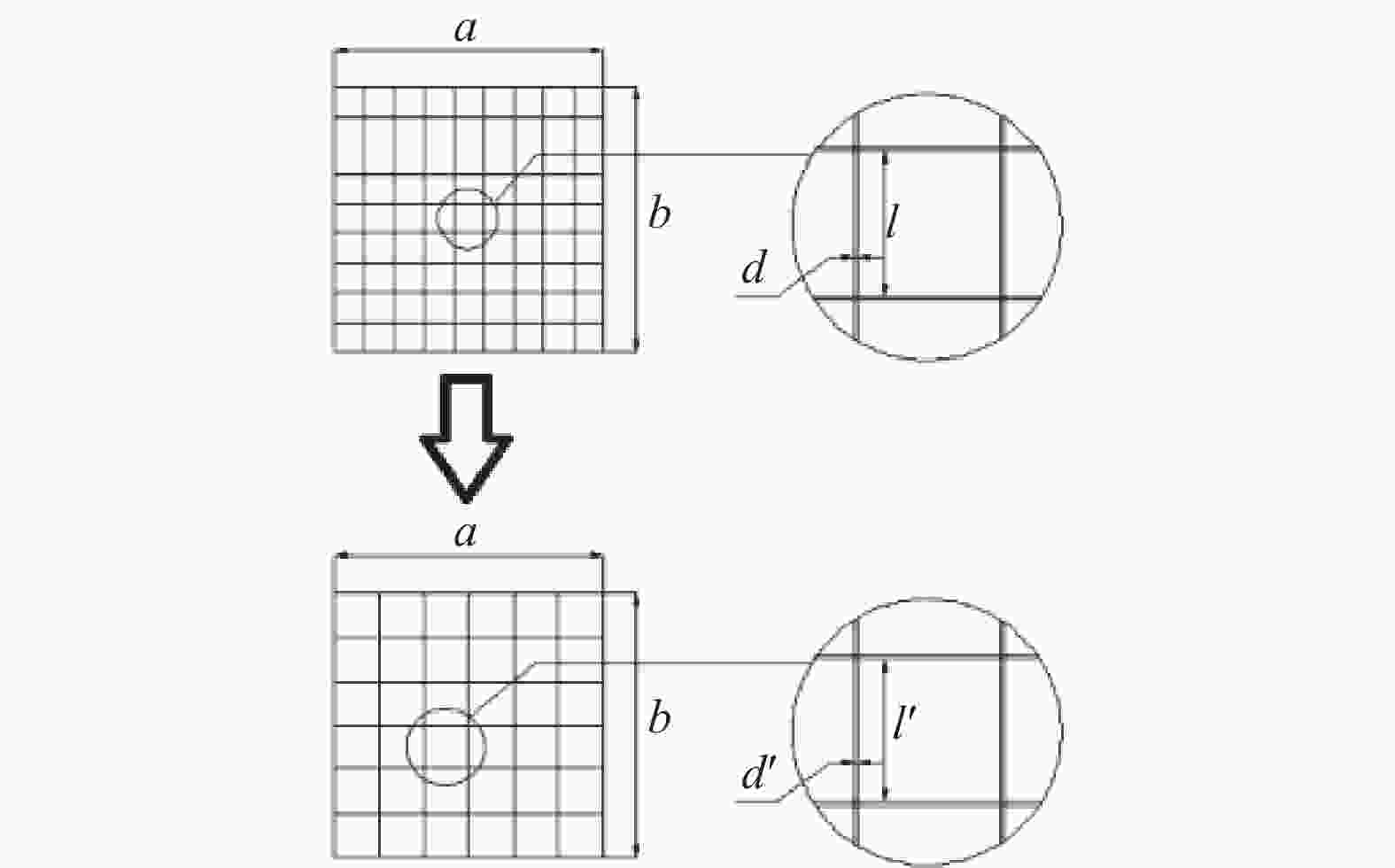
由于网衣与纲绳直径差别较大，需要分别考虑网衣和纲绳的水动力和海生物附着情况，根据网目群化方法，保证密实度相同的情况下进行等效。设单片网衣尺寸为$a \times h$，a为网衣的长度，h为网衣的宽度；网衣线径为d，网目边长为$ l $，群化后线径为D，边长为L，如图5所示，投影面积可按式（1）和式（2）计算。

Figure 5.  Net-grouping process

式中：

$S_{\mathrm{n}}$、$S_{\mathrm{N}}$——网目群化前后的网衣密实度。

根据网衣密实度相等：$S_{\mathrm{n}} = S_{\mathrm{N}}$，则可得出：

整个网衣投影面积$ A = ahP $，考虑海生物以后网衣等效线径为${d_{\mathrm{h}}}$，对于单个网孔的投影面积见式（4）：

设${d_{\mathrm{h}}} = d$，${D_{\mathrm{h}}}$为考虑海生物后网目群化的等效线径，根据式（3）和式（4），可得：

建立网衣群化模型，流程如图6所示。

Figure 6.  Step 3: Net-grouping equivalent

风机基础导管架结构和网衣结构相对于波长参数属于细长杆件，即$ \dfrac{D}{L}\leqslant 0.2 $，这类构件的波浪载荷可用Morison公式计算，见式（6）。Morison公式分为拖曳力和惯性力两部分。网衣水动力载荷惯性力占比很小，因此C_m可以保守按照1.2来考虑。拖曳力主要受网衣C_d值和投影面积影响。

式中：

${F_{\mathrm{D}}}$、${F_{\mathrm{I}}}$ ——拖曳力与惯性力；

${C_{\mathrm{d}}}$、${C_{\mathrm{m}}}$ ——拖曳力系数与惯性力系数；

$\rho $ ——海水密度（kg/m³）；

A ——构件横截面面积（m²）；

V ——构件体积（m³）；

U和$\dfrac{{\partial U}}{{\partial t}}$——水质点的水平速度（m/s）和加速度（m/s²），$U|U|$表示水质点速度具有方向性变化。

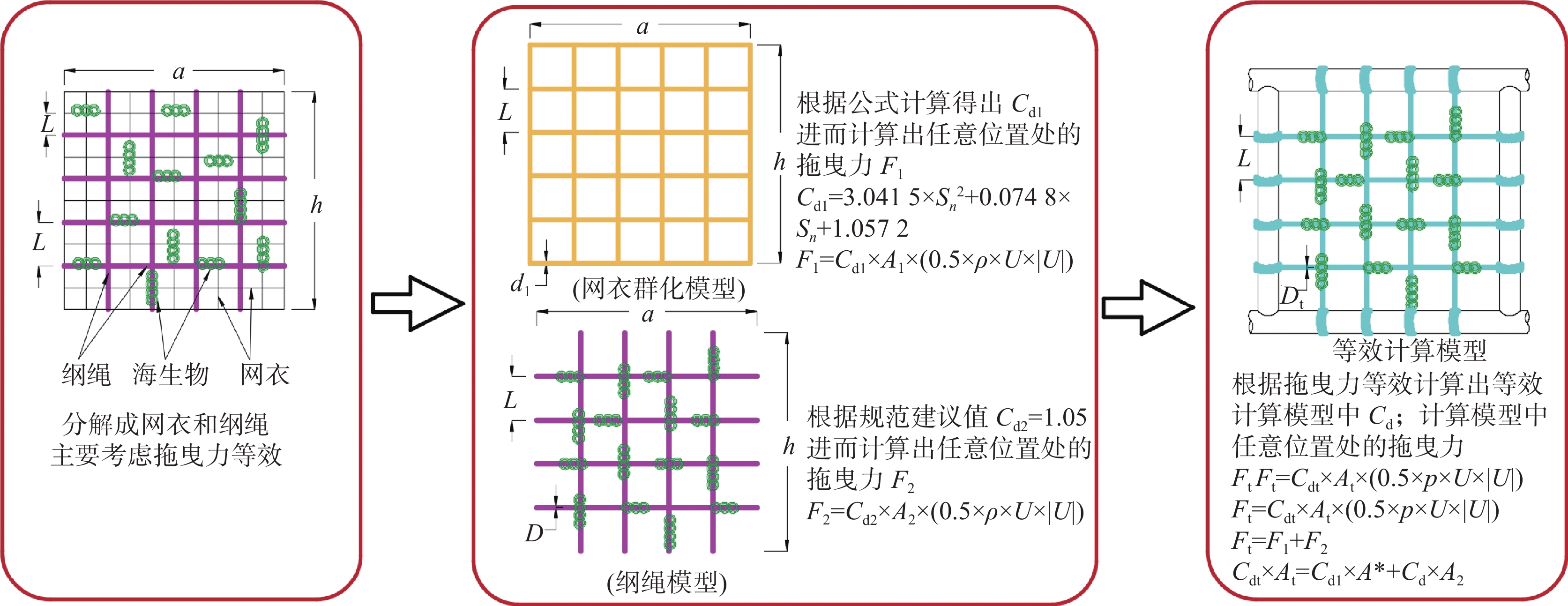
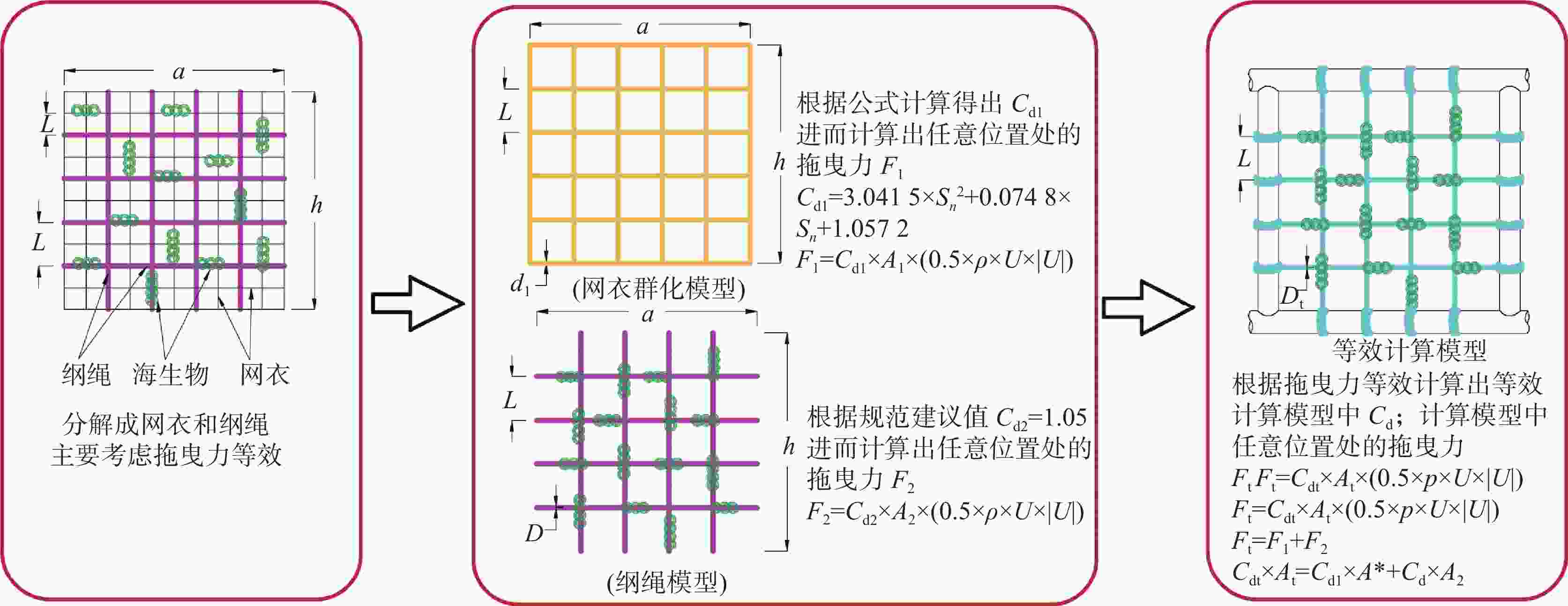
带有海生物的网衣，一般采用规范推荐的经验公式，拟合得到网衣阻力系数${C_{{\mathrm{d}}1}}$与网衣密实度$S_{\mathrm{n}}$的关系见式（7）。

设${d_{\mathrm{g}}}$为纲绳线径，海生物厚度为${T_{\mathrm{h}}}$，L为纲绳的边长，纲绳阻力系数为${C_{{\mathrm{d}}2}} = 1.05$；${C_{{\mathrm{dt}}}}$为最终模型中考虑网衣和纲绳及海生物以后的阻力系数，${D_{\mathrm{t}}}$为等效线径，则整个网衣考虑海生物附着的水动力系数${C_{{\mathrm{dt}}}}$可根据式（8）求出。

为了保证模型中海生物质量等效，简化前后海生物截面积需要相等，设L₁为网衣总线长，L₂为纲绳总线长，有如式（9）所示关系：

式（9）可以求出等效线径${D_{\mathrm{t}}}$，将${D_{\mathrm{t}}}$带入式（8）可得出最终等效阻力系数${C_{{\mathrm{dt}}}}$。

为了保证简化前后网衣和纲绳重量等效，简化前后截面积需要相等，其中简化前网衣的单位面积密度为${\rho _1}$，纲绳的单位长度密度为${\rho _2}$，设t为模型中等效圆管壁厚，$t = {{{{D_{\mathrm{t}}}}/{20}} {20}}$，则根据式（10）可求出等效圆管密度为${\rho _3}$：

至此模型中等效圆管的直径${D_{\mathrm{t}}}$、等效壁厚t、等效密度${\rho _3}$、等效阻力系数${C_{{\mathrm{dt}}}}$均可求出。网箱水动力性能等效过程如图7所示。

Figure 7.  Step 4: Equivalent hydrodynamic performance

为了验证网衣群化等效载荷计算方法的可靠性，选取单层网衣进行水动力计算，该网衣长度为10.8 m，宽度为1.08 m，其他参数如表1所示。根据模型参数建立数值模型，如图8所示。网衣群化等效后的等效网衣参数如表2所示，相应的数值模型如图9所示，为了减少模型尺寸对计算的影响，等效模型上下排杆件采用一半直径。网衣四角点采用铰接边界。

Figure 8.  Original plane net model

Figure 9.  Equivalent model of plane net after net-grouping

采用波高为9 m，周期为8 s的规则波，考虑波浪与网衣不同夹角，分别计算22.5°、45°、67°和90°工况下原始网衣模型和网衣群化等效模型的波浪力，计算结果如表3所示。由计算结果可知，波浪与网衣夹角22.5°时误差最大，为6.952%，波浪与网衣呈90°时误差仅1.818%，误差随着夹角的增大而减小，都能满足工程计算精度要求。

为了验证具有网衣和纲绳的网箱的波浪载荷计算方法的可靠性，选取单片网衣和纲绳组合结构进行水动力计算，该结构长度为10.8 m，宽度为1.08 m，其他参数如表4所示。根据模型参数建立数值模型，如图10所示。

Figure 10.  Model of original plane net with tensile rope

根据上文提出的网衣+纲绳等效方法，对模型进行简化，简化的模型参数如表5所示，相应的数值模型如图11所示，简化模型中网衣水动力占比较小，上下排杆件直径无需减半。

Figure 11.  Equivalent model of plane net with tensile rope

同样采用波高为9 m，周期为8 s的规则波，考虑波浪与网衣不同夹角，分别计算22.5°、45°、67°和90°工况下原始网衣+纲绳模型和等效网衣+纲绳模型的波浪力，计算结果如表6所示。由计算结果可知，波浪与网衣+纲绳模型夹角90°时误差最大，为1.987%，波浪与网衣+纲绳模型呈22.5°时误差仅0.964%，误差随着夹角的增大而增大，都能满足工程计算精度要求。

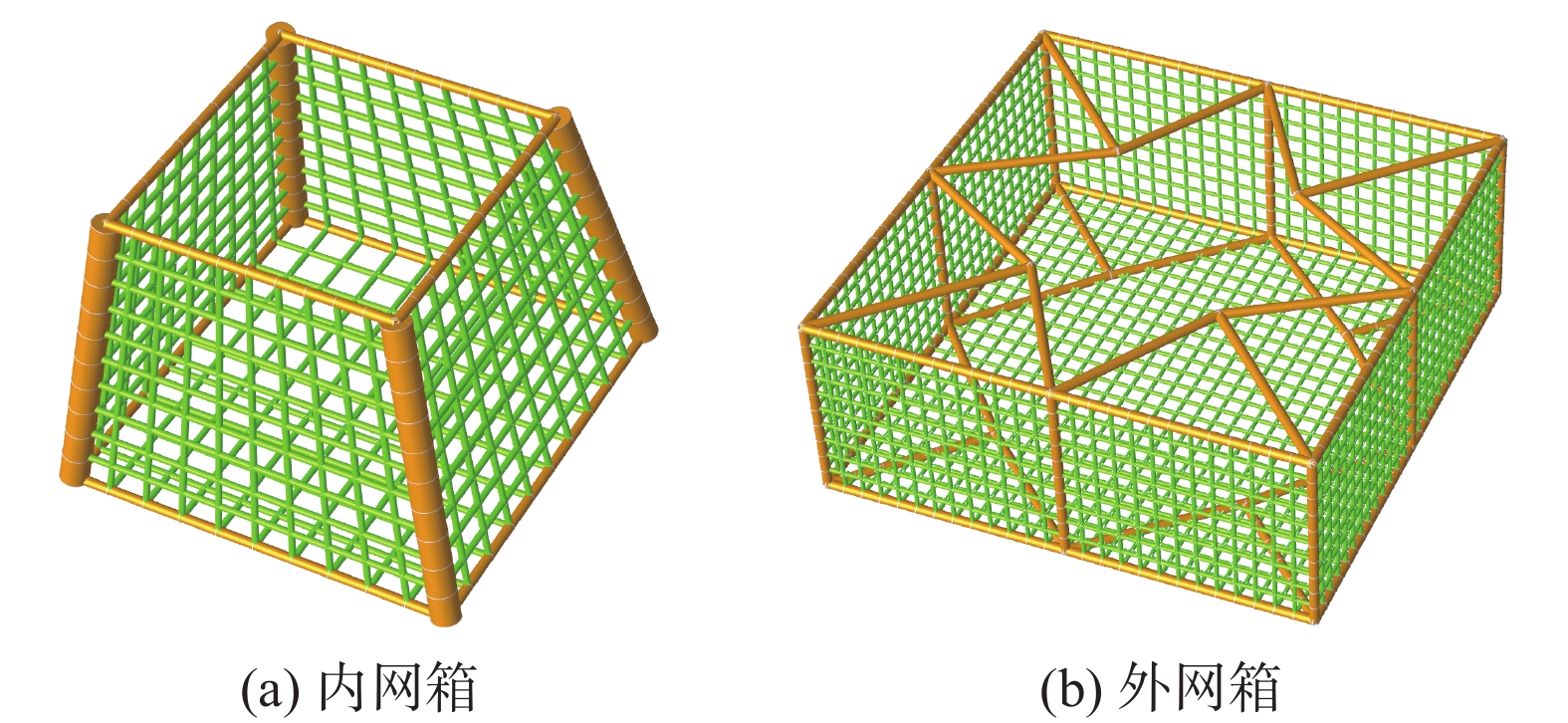
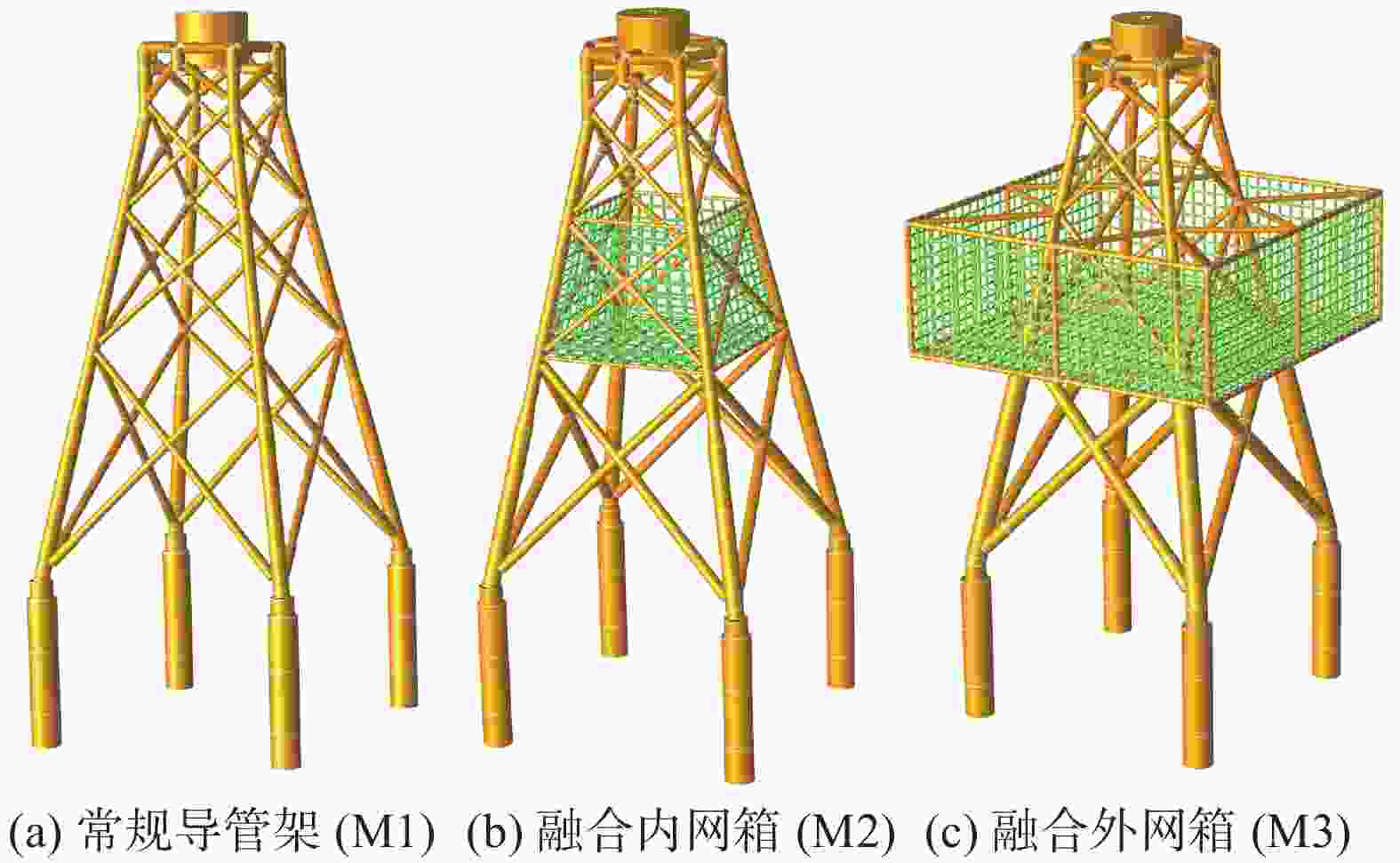
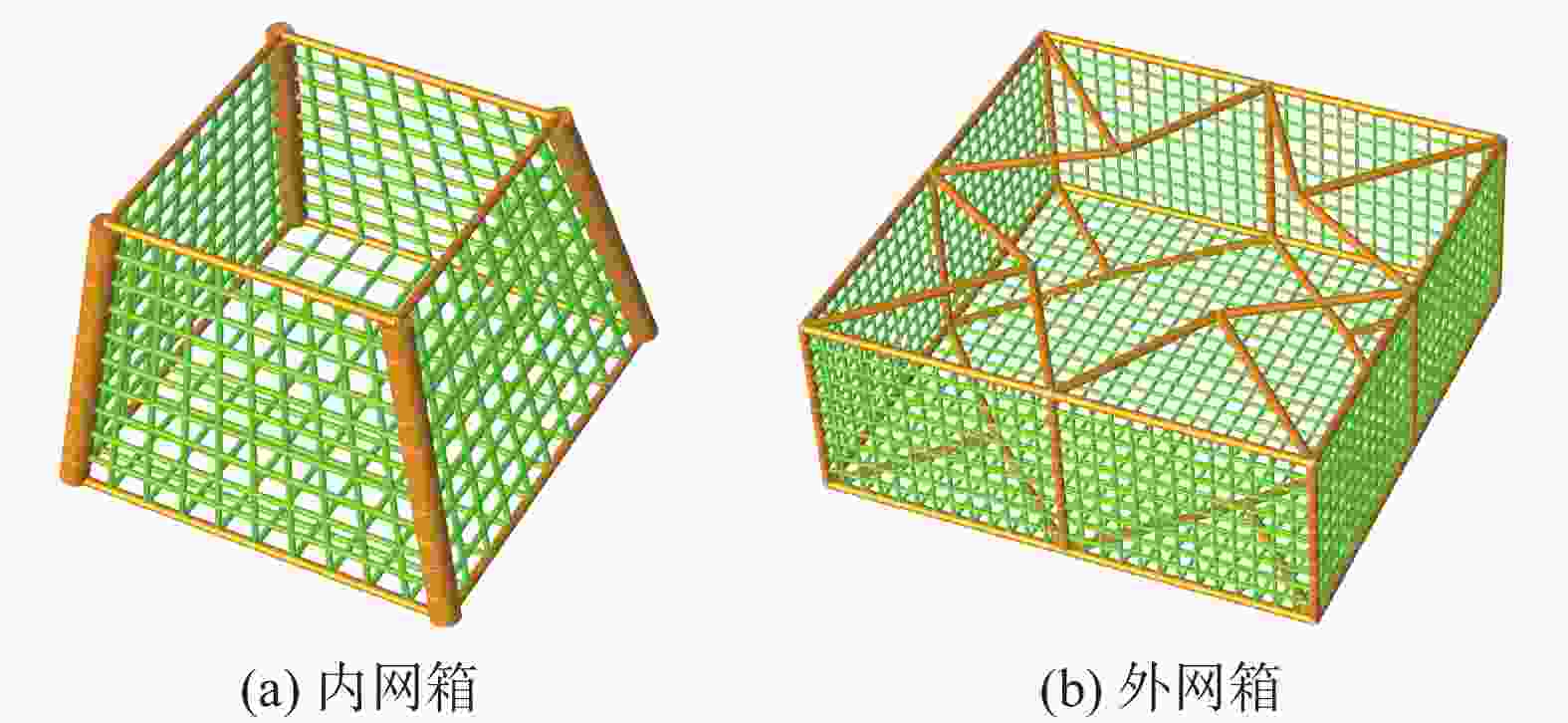
设计适用于14 MW海上风机的导管架基础（M1），导管架顶法兰高程26 m，导管架总高度74 m。风机基础主腿采用直径为1.45 m和1.8 m、壁厚为50~80 mm，在标高−12 m、+3.4 m和15.5 m处设斜拉圆管。采用4根直径3.3 m的钢管桩固定于海床上，桩长约为95 m，桩顶高程为−38 m，水深53 m，桩底高程为−135 m，桩入泥深度为82 m，分别在常规导管架内外添加养殖网箱，得出2种不同的海上风机基础加养殖网箱的融合结构（M2和M3）。M2在导管架基础结构主腿围成的4个立面和横撑围成的2个底面布置网衣，形成完整的养殖网箱，4个立面网衣布置相同。M2网箱顶面长为14.87 m，宽为14.87 m，底面长为20.5 m，宽为20.5 m，网箱高15.9 m，容积5 098 m³。M3在导管架基础结构主腿外设置4个立面和横撑组成完整养殖网箱。M3网箱顶面长为39 m，宽为39 m，网箱高15.9 m，容积24 184 m³。

为了评估海上风机与养殖网箱融合系统的动力性能，在SACS中对M1、M2和M3进行了模拟。根据实际勘察的海底岩土数据编制桩土文件，利用SACS中PSI模块进行分析，实现桩-土相互作用的边界约束处理。桩基础设计计算采用p-y曲线法（包含p-y曲线、q-z曲线和t-z曲线）。图12（a）是14 MW海上风机基础常规导管架设计（M1），图12（b）和图12（c）分别是融合内网箱（M2）和外网箱（M3）的设计。材料属性如表7所示。

Figure 12.  Jacket foundation design for 14 MW wind turbine

目前大型网箱均由超高分子材料制造的网衣和纲绳组成。为了减少计算量提高计算效率，网箱片体通常简化为圆管结构，圆管构件具有等效直径d_model、等效壁厚t_model和等效密度ρ_model，如图13所示。

Figure 13.  Net cage models

极端工况波浪和流采用重现期为50 a的环境条件。采用Morison公式与高阶流函数计算波浪力，同时考虑波浪的非线性。平台水下部分构件的海流载荷可按式（11）计算：

式中：

${F_{{\text{current}}}}$ ——海流载荷（kN）；

${\rho _{\mathrm{w}}}$ ——海水密度（t/m³）；

${\nu _{{\text{current}}}}$ ——设计海流流速（m/s）；

A ——构件在与流速垂直平面上的投影面积（m²）。

设计流速如表8所示。

作用在杆件上面的风载荷由式（12）计算：

式中：

${F_{{\text{wind}}}}$ ——风载荷（kN）；

${\nu _{{\text{wind}}}}$ ——风速（m/s）；

${C_{\mathrm{S}}}$ ——形状系数；

${A_{{\mathrm{wind}}}}$ ——构件在与风速垂直平面上的投影面积（m²）。

14 MW风机载荷施加在SACS模型中基础顶法兰处，而将风、浪、流载荷施加于下部结构。14 MW风机载荷如表9所示。

纲绳安装时需要施加一定预应力，等效后的网箱采用固结的方式与导管架进行连接。计算分析考虑了桩土作用，地质参数选取海洋某风场典型机位作为参考。模型中均采用管单元进行模拟和计算。

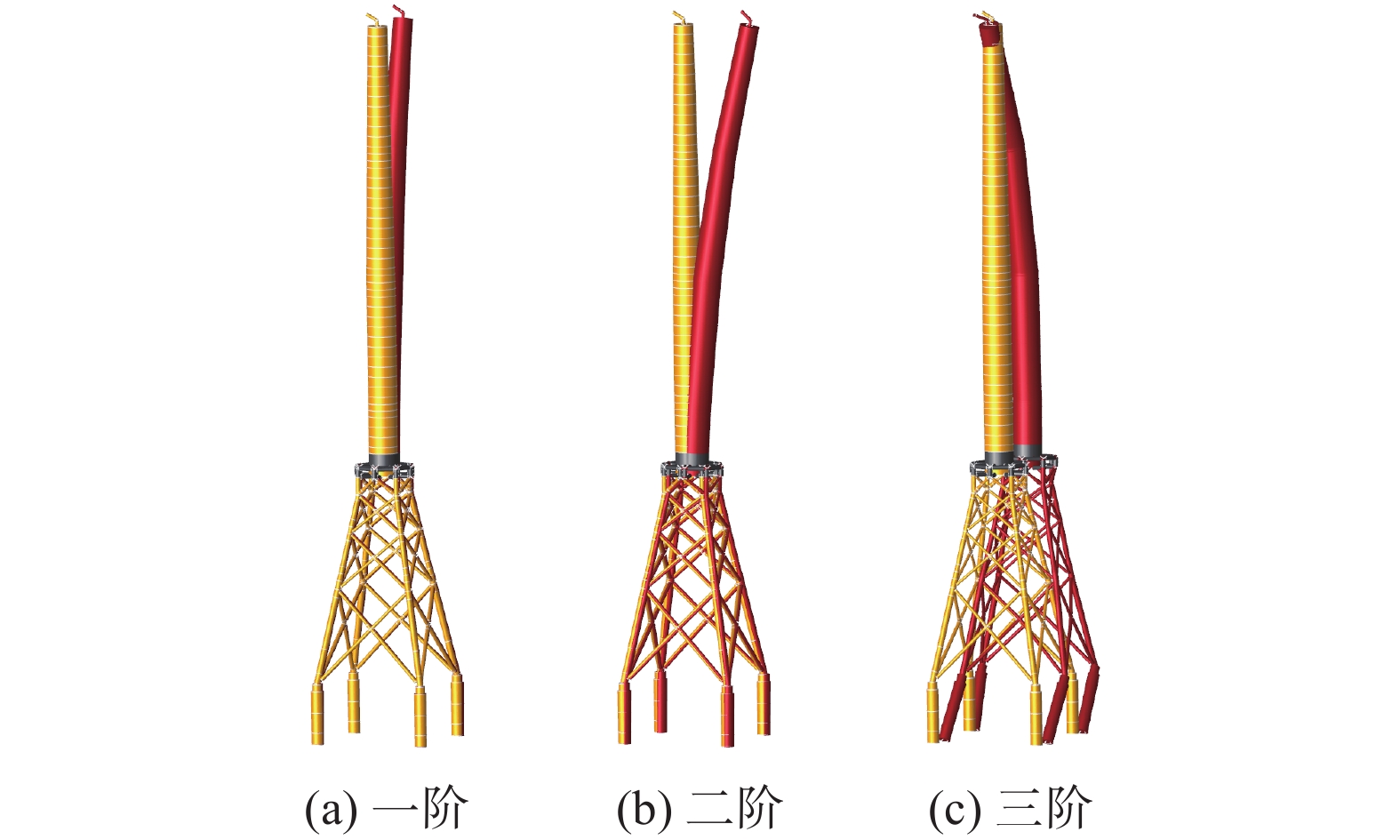
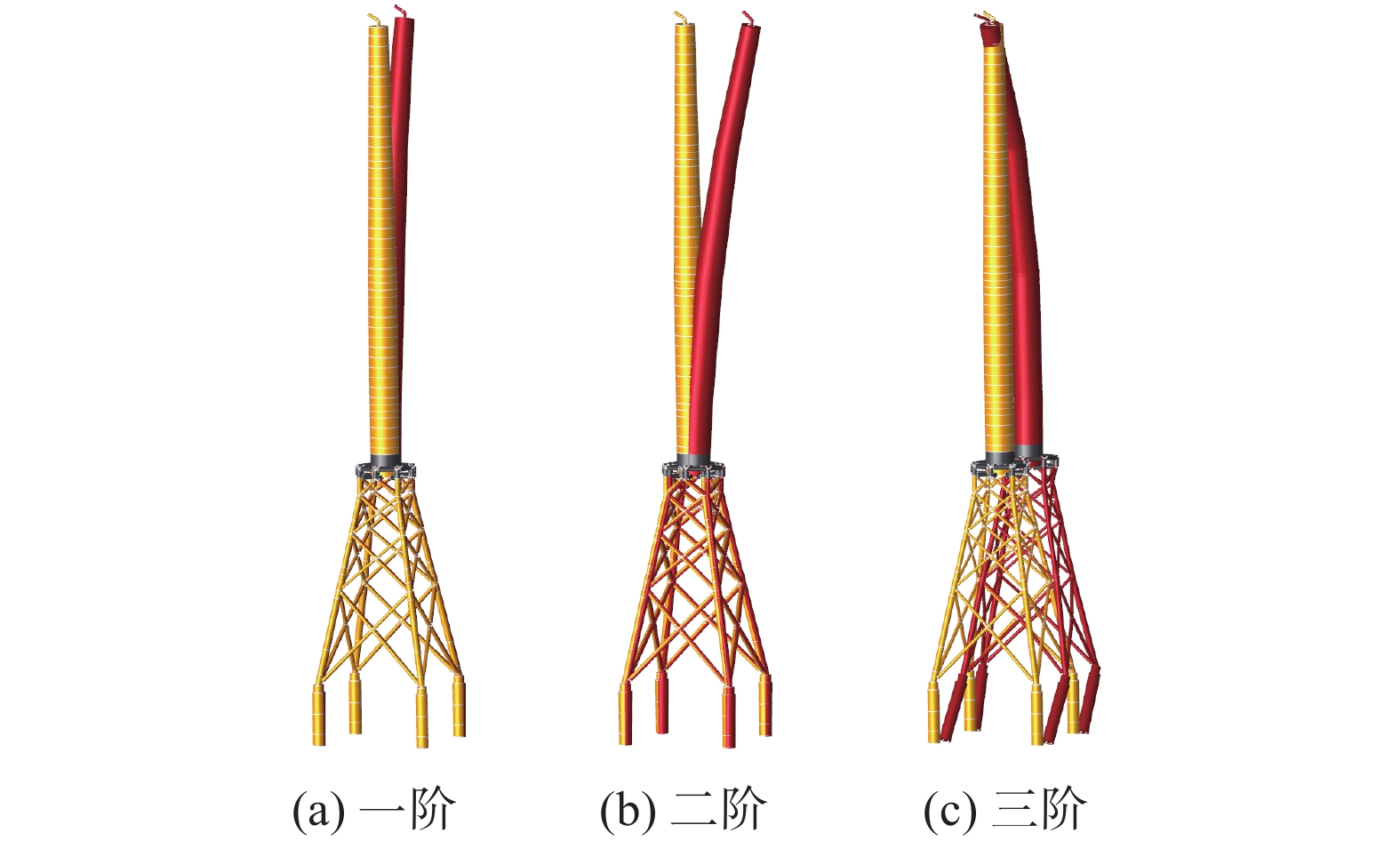
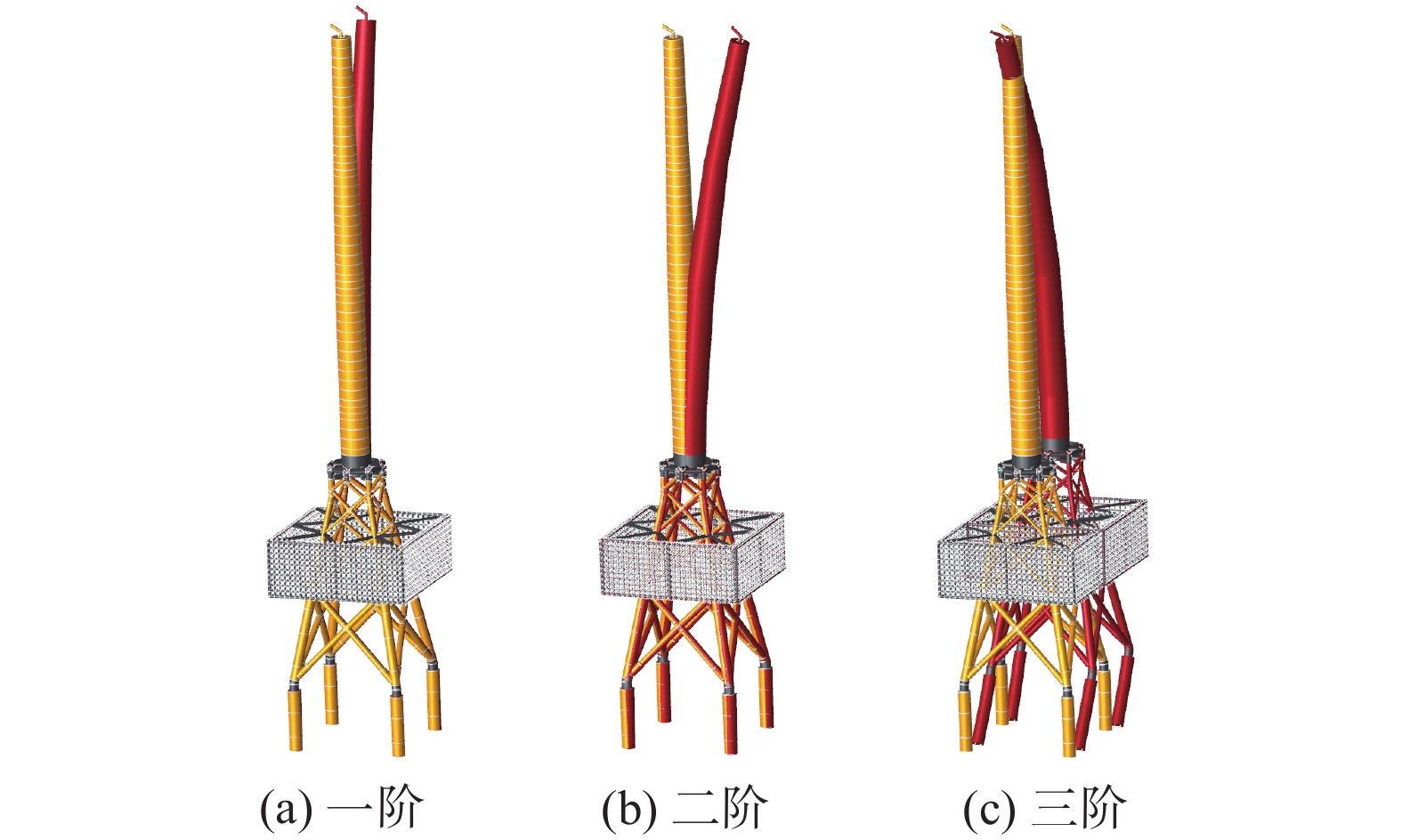
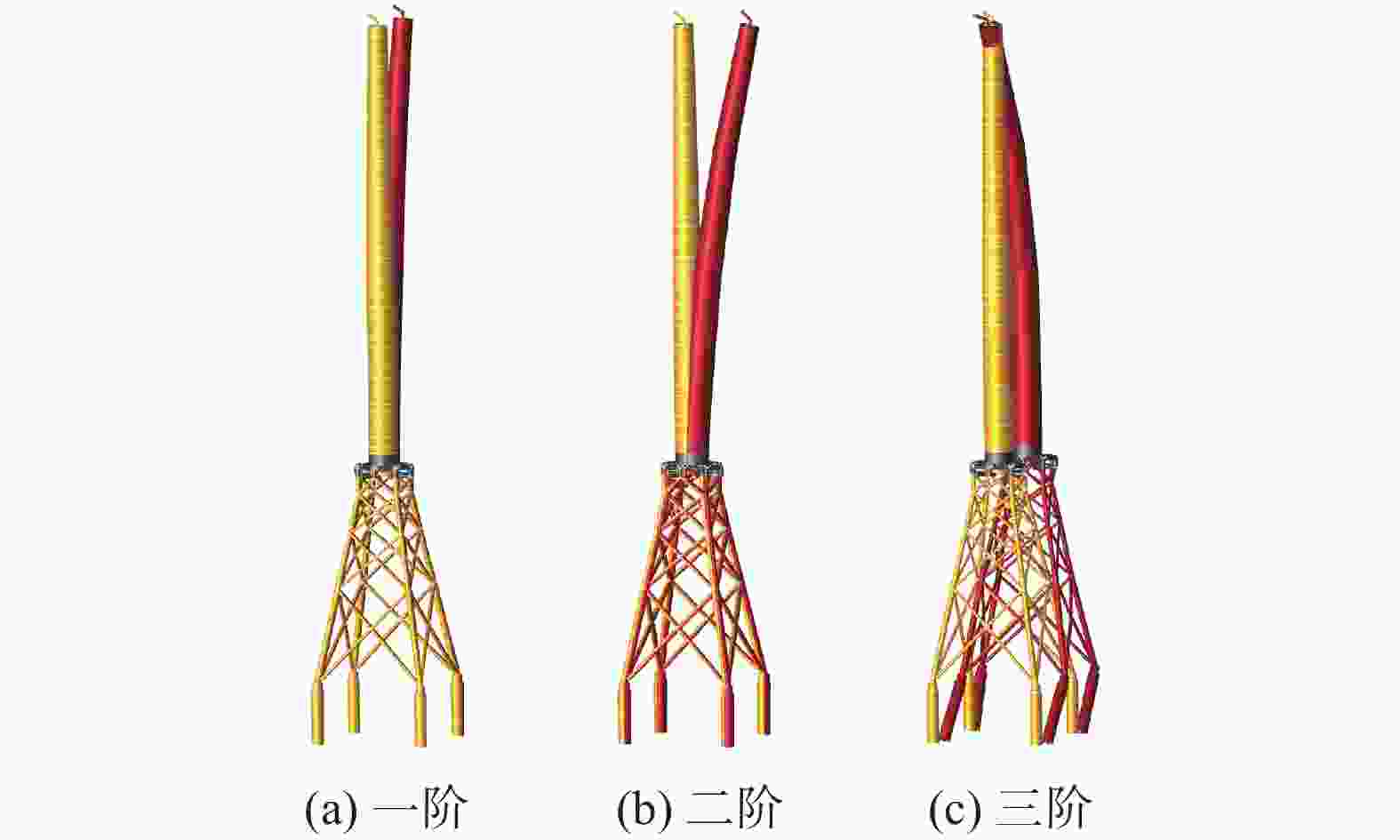
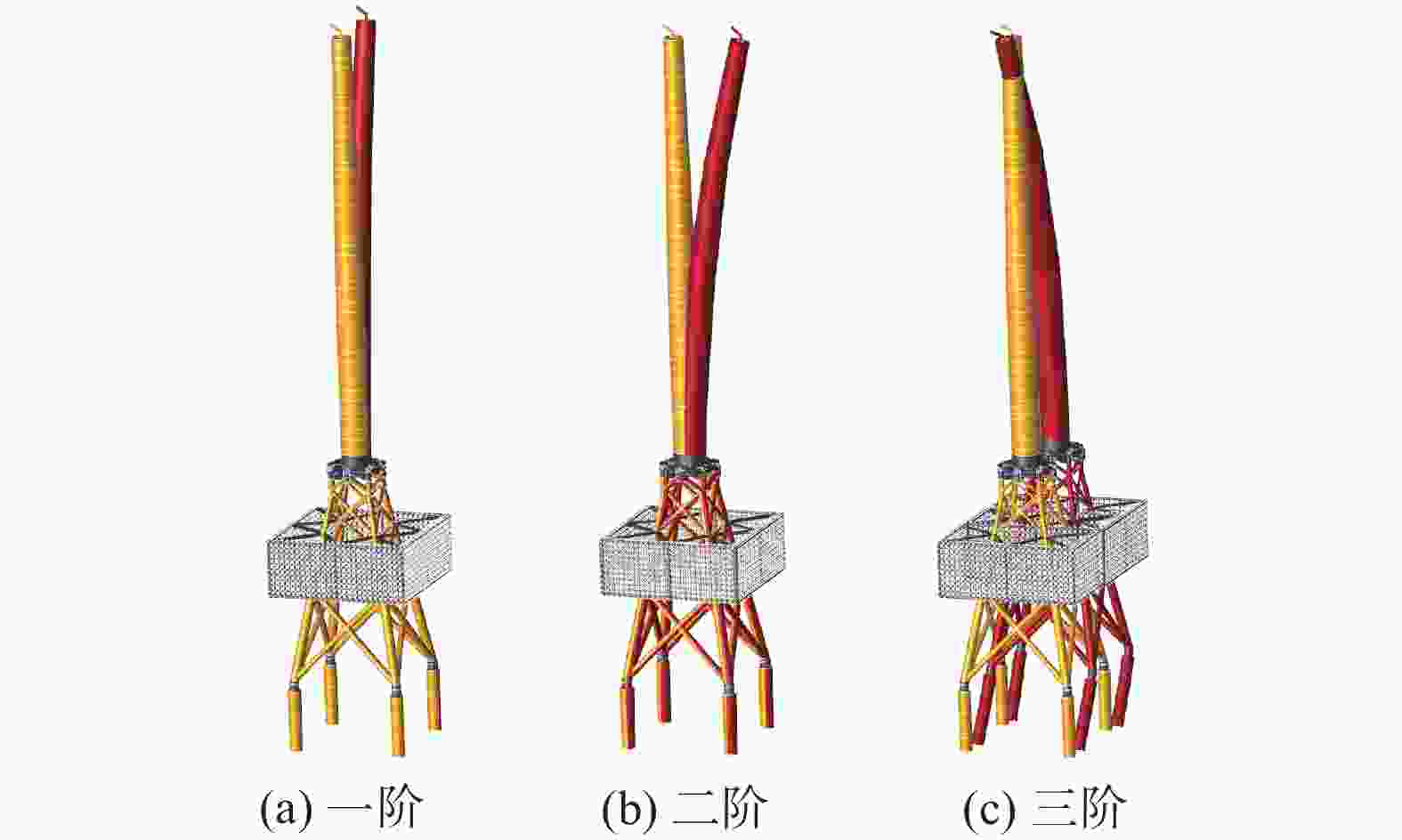
模态分析主要是分析结构的模态，模态的数量应当足够多使得参与分析的质量达到要求。采用SACS内置的分析模块，可得到M1、M2和M3结构的模态及质量矩阵。M1、M2和M3前三阶模态分别如图14、图15和图16所示，其中M2和M3考虑清洁网衣的工况。

Figure 14.  First three order modes of M1

Figure 15.  First three order modes of M2

Figure 16.  First three order modes of M3

从图14可以看出，M1第一、第二阶为塔筒X、Y方向平动；第三阶为导管架+塔筒平动，前三阶的自振频率分别为0.217 Hz、0.219 Hz、0.648 Hz。

从图15可以看出，M2第一、第二阶为塔筒X、Y方向平动；第三阶为导管架+塔筒平动，前三阶的自振频率分别为0.219 Hz、0.221 Hz、0.594 Hz。

从图16可以看出，M3第一、第二阶为塔筒X、Y方向平动；第三阶为导管架+塔筒平动，前三阶的自振频率分别为0.223 Hz、0.225 Hz、0.570 Hz。同时，为了避免结构发生共振，结构整体的一二阶固有频率需避开风机转动产生的激励频率范围0.195~0.32 Hz，上述结果均满足设计要求。

内外网箱融合一二阶频率仅引起0.002~0.006 Hz的变化，而三阶频率引起了0.054~0.078 Hz的变化。一二阶阵型主要以塔筒的变形为主，因此网箱的增加对塔筒一二阶振型的影响可以忽略不计；第三阶阵型主要以导管架的变形为主，网箱的增加影响了模型质量、刚度及阻尼，因此对三阶频率影响较大。

塔顶考虑风机载荷，基础结构施加风、浪、流载荷施，M2和M3分别考虑清洁网衣和海生物附着的网箱载荷，进行不同工况下的静力分析。在计算波浪﹑流荷载时，非结冰情况下波浪和流同时存在，应选择波浪和流作用在相同方向，水质点的运动特征应考虑波浪和流的联合作用，因而应将波浪和流在模拟在同一荷载工况。波﹑流的方向至少取8个方向，方向为0°、斜向、90°、斜向、180°、斜向、270°和斜向。斜向作用方向的确定应通过方向搜索得到，通过比较不同角度下导管架基底剪力和倾覆力矩的值，从而确定最大基底剪力和最大倾复力矩的斜向方向。

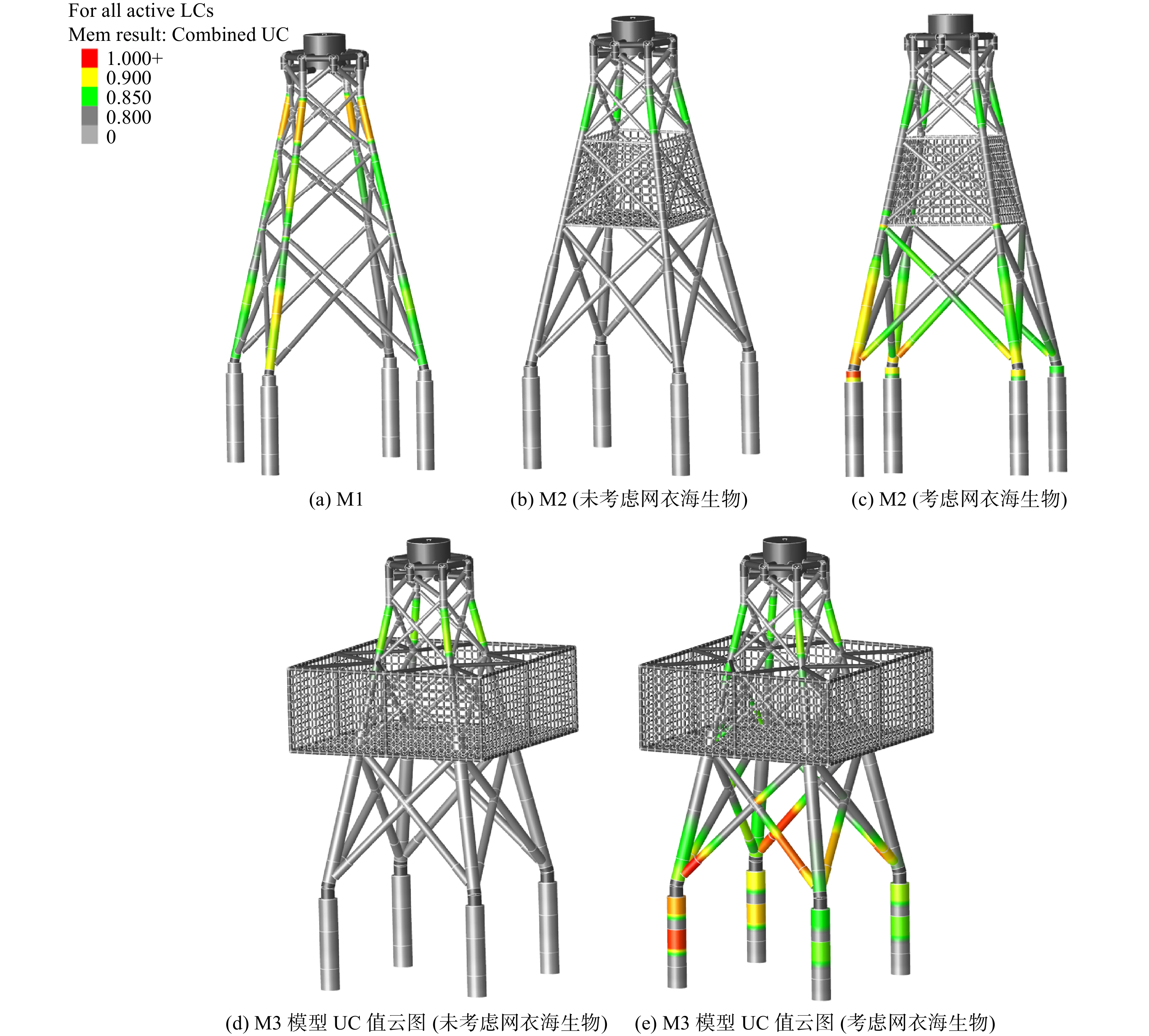
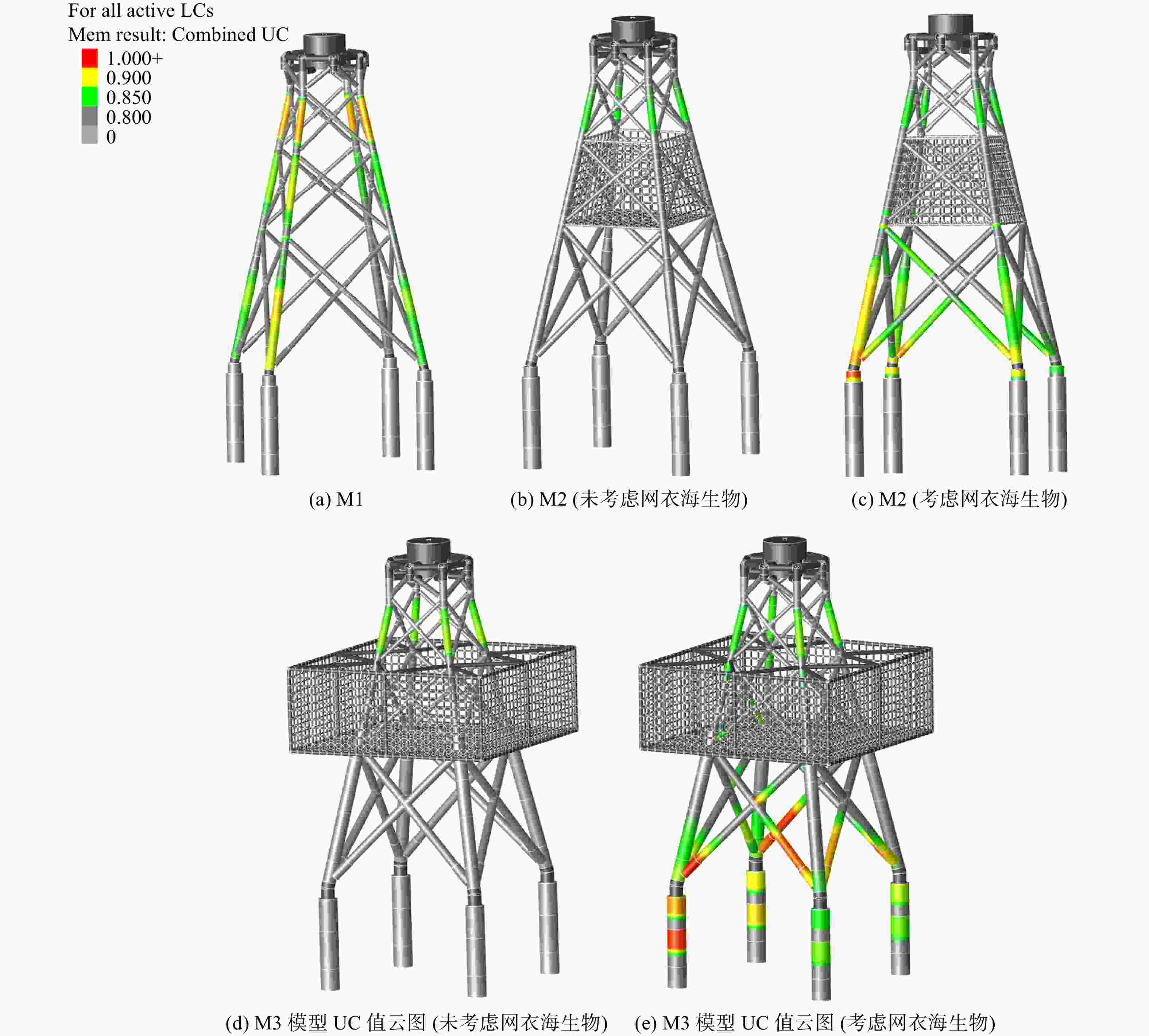
《海上风电场工程风电机组基础设计规范》（NB/T 10105－2018）中规定，导管架基础顶法兰最大允许总转角为0.5°，其中安装偏差为0.25°，计算最大转角为0.25°，即基础顶法兰最大允许水平倾角为0.004 36弧度。图17分别计算了5种工况：单独导管架转角工况，不考虑网衣海生物内网箱融合的转角工况，考虑网衣海生物内网衣网箱融合的转角工况，不考虑网衣海生物外网箱融合的转角工况，考虑网衣海生物外网衣网箱融合的转角工况。网箱融合后导管架主腿斜撑及钢管桩均需要不同程度的加强，加强后5种工况基础顶法兰处水平转角为0.004弧度，均满足规范设计要求。

Figure 17.  UC values of jacket foundation

UC（Unity Check）值是指材料的工作应力与许用应力的比值，是校核结构在不同载荷组合下是否满足强度设计要求的重要参数。在结构设计中，所有杆件的UC值不能大于1。从图17的计算结果中可以看出，M1导管架最大UC值为0.936，发生在主腿顶段；不考虑海生物附着时，M2导管架最大UC值为0.850，发生在主腿顶段；考虑海生物附着时，M2导管架最大UC值为0.977，发生在主腿底部直段；不考虑海生物附着时，M3导管架最大UC值为0.879，发生在主腿顶段；考虑海生物附着时，M3导管架最大UC值为0.979，发生在钢管桩非灌浆段。

本文设计了2种适用于14 MW海上风机导管架基础与养殖网箱融合的结构形式。提出新型网箱等效建模方法，极大减少了工作量和提高计算效率，该等效方法满足网衣质量相等，网衣附加海生物质量相等，网衣水动力性能等效的要求。基于Morison模型，考虑非线性波的影响，根据提出的网箱等效建模方法在SACS中建立14 MW海上风机导管架基础和网箱融合系统的有限元模型，对网箱进行简化，对常规风机基础设计和与网箱融合的设计在风、浪、流条件下进行静力分析。根据上述研究，可以得出以下结论：

1）根据14 MW风机设计载荷和海洋水文条件，建议采用导管架基础，结合海上风电与海洋养殖融合发展需求，可以在导管架基础上设计内置网箱或外置网箱，经过初步的静力计算，在风机载荷、风浪流作用下的导管架基础和导管架基础与网箱融合系统的刚度、强度计算满足规范要求。

2）内外网箱与导管架融合设计对整机频率一二阶影响较小可忽略不计，对三阶频率影响较大，设计和计算时需要注意三阶以上频率的变化对波浪响应及波浪疲劳的影响。

3）通过计算发现转角工况是控制工况，内外网箱导管架模型均需要局部加强才能满足规范设计要求，内网箱加强后导管架用钢量增加了409 t，外网箱加强后导管架用钢量增加了1 204 t。通过测试网衣海生物对转角影响较小，基础顶法兰转角主要影响因素为网箱大小和网箱融合方式。

4）5种工况ULS工况计算杆件的UC值均小于1.0满足设计要求，通过结果对比发现网箱的融合设计对导管架强度UC影响较大，主腿和斜撑都需要不同程度的加强。是否考虑网衣海生物对导管架局部UC影响较大，导管架主腿和斜撑的UC值会增加一倍以上。