-
电厂在役运行阶段，汽水管道及工业管道由于介质长期冲刷，存在加速腐蚀情况，严重威胁电厂安全运行[1]。现阶段针对电厂在役运维的技术手段主要为超声波检测，对于检测前序准备及检测前提条件要求较高，增加了现场实施难度。
脉冲涡流法，具有穿透距离大，检测速度快等优点，可以作为一种新型无损检测技术应用于核电厂在役运维[2]。在激发线圈加载方波电流，通过检测线圈检测待检部件内涡流电磁场的变化来检测剩余壁厚。针对核电厂带保温层管道，其保温层厚度范围为50～100 mm，脉冲涡流可以穿透保温层对待检管道剩余壁厚进行评估，使用脉冲涡流进行管道初筛，可以缩短电厂检修工期，提高发电经济效益。
现有铁磁管道脉冲涡流检测技术，主要根据感应电压与时间绘制关系曲线，通过对数变换等手段截取曲线变化前后期的特征参数。黄平捷等[3-4]对多层厚度电涡流检测反演算法及实验进行了研究。贺光琳[5]研究了涡流检测缺陷反演算法以及直接数字频率合成技术。Dehaan等[6]以双对数坐标系下时域感应电压拐点时间作为检测特征量来检测铁磁管道壁厚的相对变化量。Cheng[7]对同时带有非金属保温层和金属保护层的碳钢管道的壁厚减薄脉冲涡流检测方法进行了研究，将理论模型简化为4层平板模型，并提取磁场衰减系数作为特征量来检测碳钢管道壁厚。柯海等[8]针对钢材腐蚀，采用特定脉冲涡流信号变换并提取，以后期感应电压直线段的斜率为特征量来反映壁厚大小或利用信号拐点来检测铁磁管道的壁厚。Xu等[9]利用差分信号峰值时间来检测铁磁管道的壁厚。
最优化方法是涡流检测中参数反演、缺陷重构的另一种有效方法。Vasić等[10]利用管道内同轴线圈的阻抗变化，来同时反演金属管道的内径和电磁参数，研究发现该方法只能反演出管道的内径以及相对磁导率与电导率的比值。Mao等[11]则基于金属管道外放置式线圈涡流检测模型的频域解析解，与线圈阻抗-频率变化曲线建立最小二乘参数反演问题，利用Levenberg-Marquardt（LM）算法同时反演铁磁管道的电导率、磁导率、壁厚、内径、线圈提离5个参数，实验结果表明，参数反演结果受迭代初值的影响较大。Xie等[12]利用脉冲涡流检测中感应电压差分信号，运用共轭梯度算法来反演双层金属管道壁内局部腐蚀减薄缺陷，论文指出，当同时反演缺陷形状的多个参数时，第一参数的选取极为重要，参数顺序选取错误，反演结果无法提取特征量，随着待反演参数的增加，这类问题会变得更加严重。
上述文献均指出同时反演多个参数时难度更大，检测结果的精度和可靠性会变差。重要原因之一是待反演参数之间存在耦合关系，当待检测参数耦合在一起时，不管是采用特征量法还是最优化参数反演法，检测信号微小的扰动，或者反演条件稍微的改变，均会导致检测结果显著的误差。
与石油、石化厂相比，核电站中存在发电机组、变电站、输电母线等大功率电器设备，其中的大电流会在整个电厂空间形成低频磁场，频率成分以50 Hz基波及其奇次谐波为主。而这个频段，会与脉冲涡流检测信号的频谱有明显重合，因此，在役机组产生的低频磁场会对脉冲涡流检测信号造成明显的电磁干扰。本文主要研究核电站低频电磁干扰下脉冲涡流检测方法的可行性和可靠性。根据管道脉冲涡流场时域解析解的基础上，建立感应电压测量值与计算值特定关系式，建立最优化参数反演问题，并结合参数之间的耦合关系式，提出1种针对核电厂带保温管道在役运维的脉冲涡流检测技术。
-
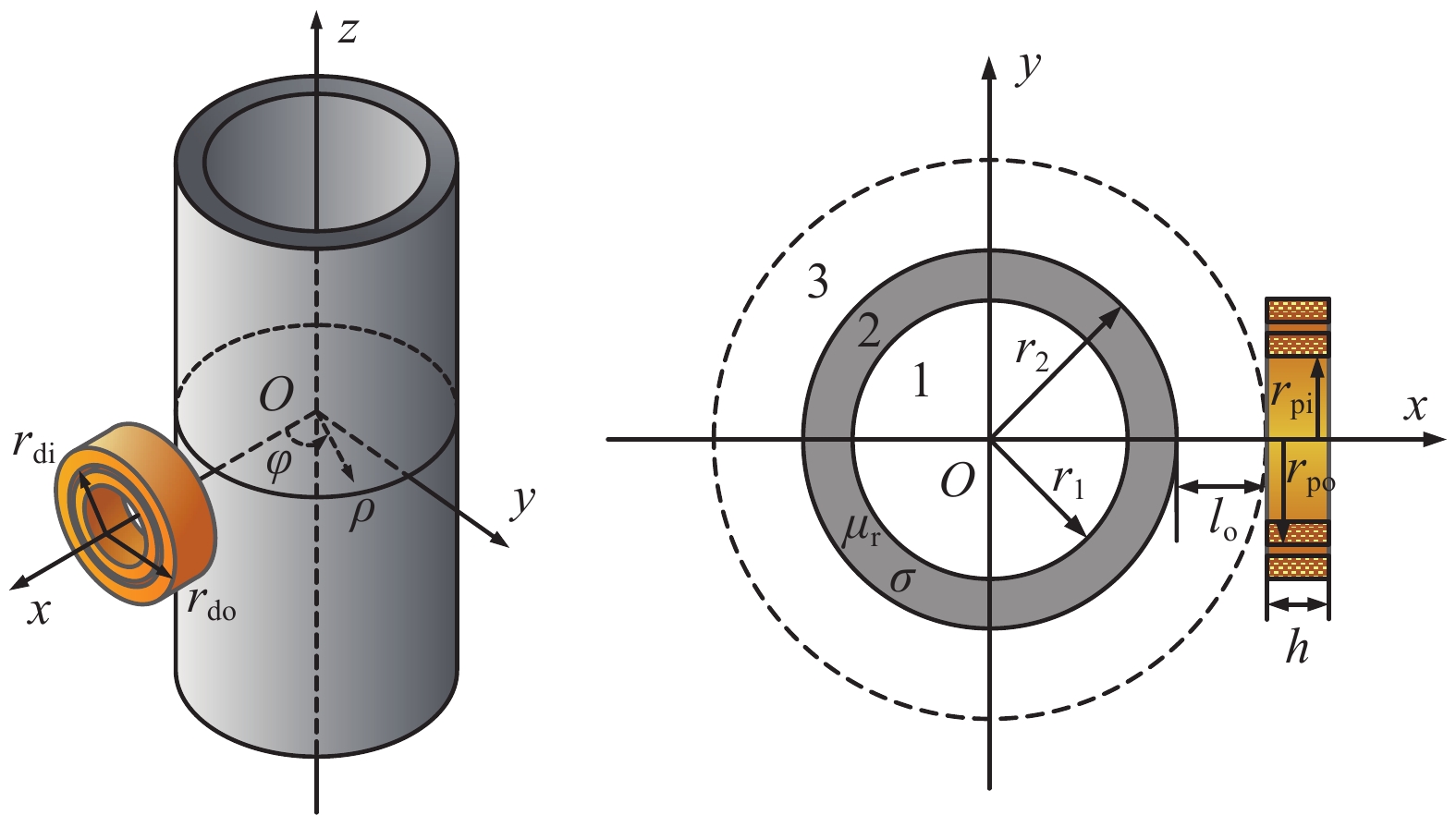
设长直导电、导磁金属管道的内半径为$ {r_1} $，外半径为$ {r_2} $，管道壁厚$ d = {r_2} - {r_1} $，电导率$ \sigma $，磁导率$ \mu = {\mu _0}{\mu _r} $（$ {\mu _0} $为真空磁导率，$ {\mu _r} $为相对磁导率）。激励线圈（下标为$ d $）和检测线圈（下标为$ p $）沿管道径向法线垂直放置在管道外，线圈高度为$ h $。如图1所示，$ {l_0} $为保温层厚度，即探头的提离距离。圆柱线圈的内半径和外半径分别为$ {r_i} $和$ {r_0} $，匝数为$ N $。建立圆柱坐标系$ O\rho \phi z $，并让$ z $轴与管道轴线重合。对管道实施脉冲涡流检测时，通过在激励线圈中通入方波电流激发待检管道模型本体的涡流场变化，涡流场变化被检测线圈接收并处理，得到待检管道模型的剩余壁厚及相关参数。
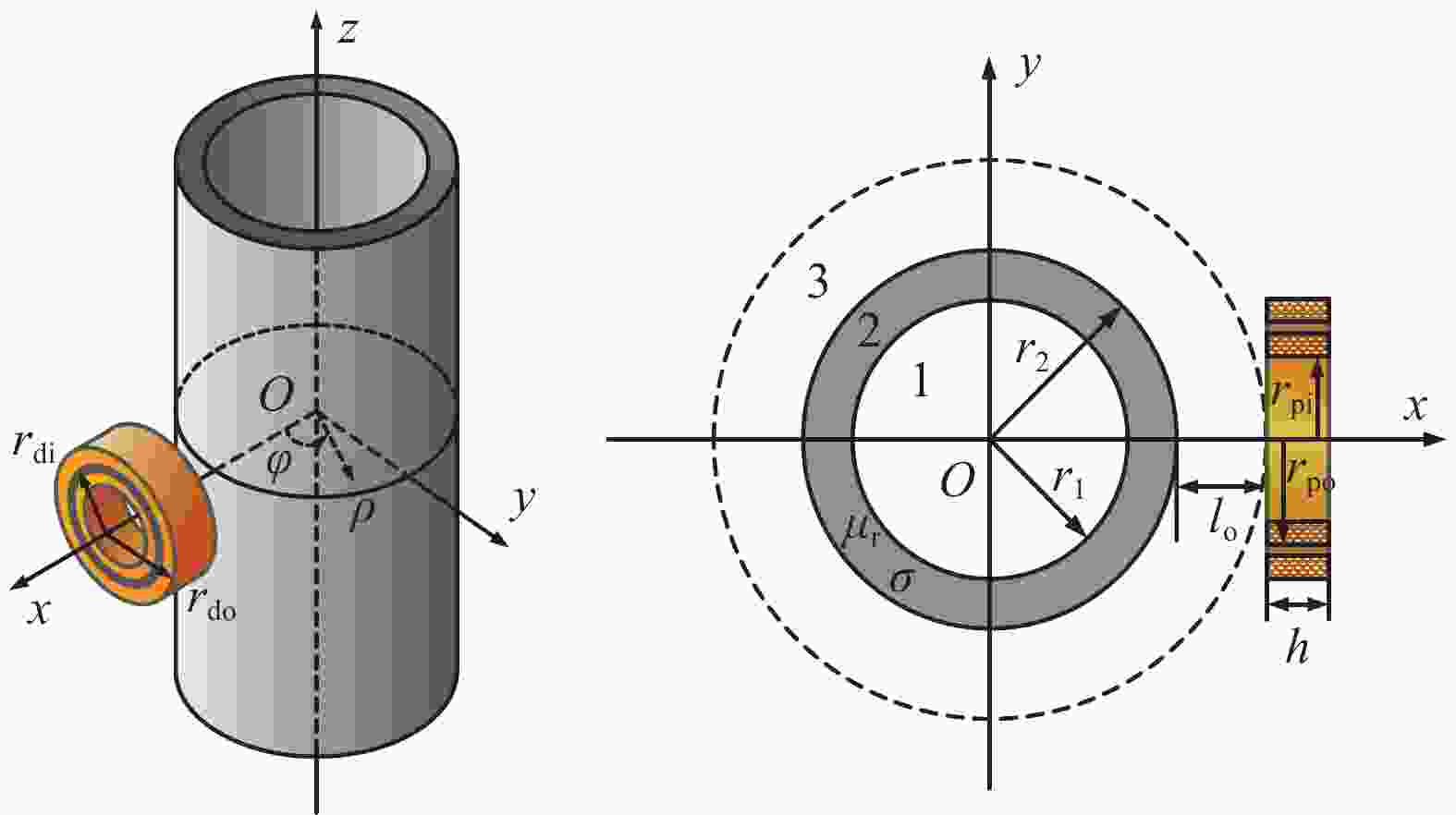
Figure 1. Pulse eddy current testing model of placing cylindrical coil vertically outside the metal pipeline
图1所示管道涡流检测模型是1个三维涡流场问题。当进行方波电流$ i(t) $激励时，引用文献[13]的结果，可以得到如下感应电压时域解析公式，如式（1）所示：
$$ \begin{split} &{u}_{{\mathrm{ec}}}\left(t\right)={i}^{{'}}\left(t\right){\int }_{0}^{+\infty }\sum _{m=0}^{+\infty }\frac{{v}_{m}{C}_{{\mathrm{d}}}\left(\lambda ,m\right){C}_{{\mathrm{p}}}\left(\lambda ,m\right)}{{\lambda }^{3}{K}_{m}^{2}\left(\lambda {r}_{2}\right)}\\&\sum _{k=1}^{+\infty }\frac{{F}_{{\mathrm{nu}}}\left({\xi }_{{\mathrm{dek}}}\right)}{{F}_{{\mathrm{de}}}^{{'}}\left({\xi }_{{\mathrm{dek}}}\right)}{\xi }_{{\mathrm{dek}}}{e}^{\frac{-{\xi }_{{\mathrm{dek}}}^{2}+{\lambda }^{2}}{\mu \sigma }t}{\mathrm{d}}\lambda \end{split} $$ (1) $$ {V_m} = \left\{ \begin{array}{l} 1,\;m = 0\\ 2,\;m \ne 0 \end{array} \right. $$ 式中：
$ {K_m}(x) $——第2类m阶修正贝塞尔函数；
$ {i^{'}}(t) $ ——方波电流的导数。
$$ {f_1}(t)*{f_2}(t) = \int_0^t {{f_1}\left( \tau \right)} {f_2}(t - \tau ){\mathrm{d}}\tau $$ “*”表示对时间的卷积。
激励线圈系数如式（2）所示：
$$ \begin{array}{l} {C_{\rm{d}}}\left( {\lambda ,m} \right) = \dfrac{{{N_{\rm{d}}}}}{{\left( {{r_{{\rm{do}}}} - {r_{{\rm{di}}}}} \right){h_{\rm{d}}}}}\displaystyle \int _{{r_2} + {l_{\rm{o}}}}^{{r_2} + {l_{\rm{o}}} + {h_{\rm{d}}}}{\mathrm{d}}x\\ \displaystyle \int _{{r_{{\rm{di}}}}}^{{r_{{\rm{do}}}}}{d_{{r_0}}}\smallint _0^{{r_0}}\left( {{C_{{\rm{sa}}}} + {C_{{\rm{sb}}}}} \right){\rm{sin}}\left( {\lambda \sqrt {r_0^2 - {y^2}} } \right)dy \end{array} $$ (2) $$ {C_{{\mathrm{sa}}}} = \frac{{x\lambda }}{{\sqrt {{x^2} + {y^2}} }}{K'_m}(\lambda \sqrt {{x^2} + {y^2}} ){\mathrm{cos}}\left( {{\mathrm{marctan}}\frac{y}{x}} \right) \text{；} $$ $$ {C_{{\mathrm{sb}}}} = \frac{{my}}{{{x^2} + {y^2}}}{K_m}(\lambda \sqrt {{x^2} + {y^2}} ){\mathrm{sin}}\left( {{\mathrm{marctan}}\frac{y}{x}} \right) \text{；} $$ 式中：
$ {N_{\mathrm{d}}} $ ——圆柱激励线圈的匝数（个）；
$ {r_{{\mathrm{do}}}} $ ——激励线圈外半径（mm）；
$ {r_{{\mathrm{di}}}} $ ——激励线圈内半径（mm）；
$ {h_{\text{d}}} $ ——激励线圈外半径（mm）。
将检测线圈几何参数代入到式（2）中得到$ {C_{\mathrm{p}}}(\lambda ,m) $。式（1）中分子和分母的表达式分别如式（3）、式（4）所示：
$$ {F_{{\text{nu}}}}\left( \xi \right) = {\beta _{\mathrm{s}}}{A_m}{D_m} - {\alpha _{\mathrm{s}}}{B_m}{C_m} - {A_m}{B_m}{r_{22}} $$ (3) $$ \begin{split} &{F_{{\mathrm{de}}}}\left( \xi \right) = {\left( {{\beta _\xi }{A_m} + {\alpha _\xi }{B_m}} \right)^2} - {\alpha _\xi }{\beta _\xi }{\left( {{C_m} + {D_m}} \right)^2} - {\beta _\xi }{A_m}\\&\left( {{C_m}{r_{22}} + {D_m}{r_{11}}} \right) + {\alpha _\xi }{B_m}\left( {{D_m}{r_{22}} + {C_m}{r_{11}}} \right) + {A_m}{B_m}{r_{11}}{r_{22}} \end{split} $$ (4) 式中：
$$ {\alpha _\xi } = - \frac{{\lambda {\mu _{\mathrm{r}}}}}{\xi } \text{；} $$ $$ {\beta _\xi } = - \frac{{{m^2}{\mu _{\mathrm{r}}}}}{{{\xi ^2}}}\left( {\frac{\lambda }{\xi } + \frac{\xi }{\lambda }} \right) \text{；} $$ Am、Bm、Cm和Dm分别为贝塞尔函数的多项式：
$$ {A_m} = {{{J}}_m}({r_1}\xi ){{{Y}}_m}({r_2}\xi ) - {{{J}}_m}({r_2}\xi ){{{Y}}_m}({r_1}\xi ) $$ $$ {B_m} = \left[ {{{{{{{J}}'}}}_m}({r_1}\xi ){{{{{{Y}}'}}}_m}({r_2}\xi ) - {{{{{{J}}'}}}_m}({r_2}\xi ){{{{{{Y}}'}}}_m}({r_1}\xi )} \right]{r_1}{r_2} $$ $$ {C_m} = \left[ {{{{{{{J}}'}}}_m}({r_1}\xi ){{{Y}}_m}({r_2}\xi ) - {{{J}}_m}({r_2}\xi ){{{{{{Y}}'}}}_m}({r_1}\xi )} \right]{r_1} $$ $$ {D_m} = \left[ {{{{J}}_m}({r_1}\xi ){{{{{{Y}}'}}}_m}({r_2}\xi ) - {{{{{{J}}'}}}_m}({r_2}\xi ){{{Y}}_m}({r_1}\xi )} \right]{r_2} $$ 其中$ {J_m}(x) $和$ {Y_m}(x) $分别为第1类和第2类m阶贝塞尔函数，$ J_m^{'}(x) $和$ Y_m^{'}(x) $分别表示其对变量x的导数。式（1）中$ {\xi _{{\mathrm{dek}}}} $是分母表达式$ {F_{{\mathrm{de}}}}(\xi ) = 0 $的第k个正实根，$ F{'_{{\mathrm{de}}}}(\xi ) $表示分母$ {F_{{\mathrm{de}}}}(\xi ) $对变量ξ的导数（$ {\xi _{{\mathrm{dek}}}} $、$ F{'_{{\mathrm{de}}}}(\xi ) $可通过数值计算方法获得）。
-
图1所示管道检测模型中，已将脉冲磁场激励下铁磁管道的磁化曲线作线性化近似处理，设相对磁导率值为1个未知常数[14]。在此，利用最小二乘法求解参数反演问题如表1所示。设被检铁磁管道的壁厚$ d $、电导率$ \sigma $和相对磁导率$ {u_{\mathrm{r}}} $为3个未知参数，设参数向量$ x = {(d,\sigma ,{u_{\mathrm{r}}})^T} $。设采集到的检测线圈两端时域感应电压数据为$ ({t_1},{u_1}),({t_2},{u_2}), \cdots \cdots ({t_m},{u_m}) $，检测线圈两端理论感应电压为$ u(x,t) $，取二者误差平方的一半的最低值进行反演[15]。
线圈参数 激励线圈 检测线圈 匝数N/个 174 1 025 高度h/mm 25.0 25.0 内半径ri/mm 20.9 20.0 外半径ro/mm 22.2 20.8 Table 1. Geometry of excitation coil and test coil
$$ \left\{ \begin{gathered} \mathop {\min }\limits_{x \in {R^3}} f\left( x \right){\text{ }}\underline{\underline {{\mathrm{def}}}} {\text{ }}\frac{1}{2}\sum\limits_{j = 1}^m {{{\left[ {{u_j} - u\left( {x,{t_j}} \right)} \right]}^2}} \\ s.t. {x_i} > 0,{\text{ }}i = 1,2,3{\text{ }} \\ \end{gathered} \right. $$ (5) 研究过程中，通过比较时域感应电压对壁厚、电导率和相对磁导率的偏导函数表达式和计算曲线，判断出3个偏导函数之间存在近似线性相关，进而分析得出在铁磁构件脉冲涡流检测中，构件电导率与壁厚，以及相对磁导率与壁厚，大体以乘积的形式耦合在一起[16]。
即在铁磁管道脉冲涡流检测中，感应电压对$ x $中各参数的偏导函数满足：
$$ \frac{{\partial {u_{{\text{ec}}}}\left( {x,t} \right)}}{{\partial \sigma }}\sigma + \frac{{\partial {u_{{\text{ec}}}}\left( {x,t} \right)}}{{\partial {\mu _{\mathrm{r}}}}}{\mu _{\mathrm{r}}} - \frac{{\partial {u_{{\text{ec}}}}\left( {x,t} \right)}}{{\partial d}}d \approx 0 $$ (6) 利用特征方程法解此一阶齐次偏微分方程（6），方程的通解可以写为[17]：
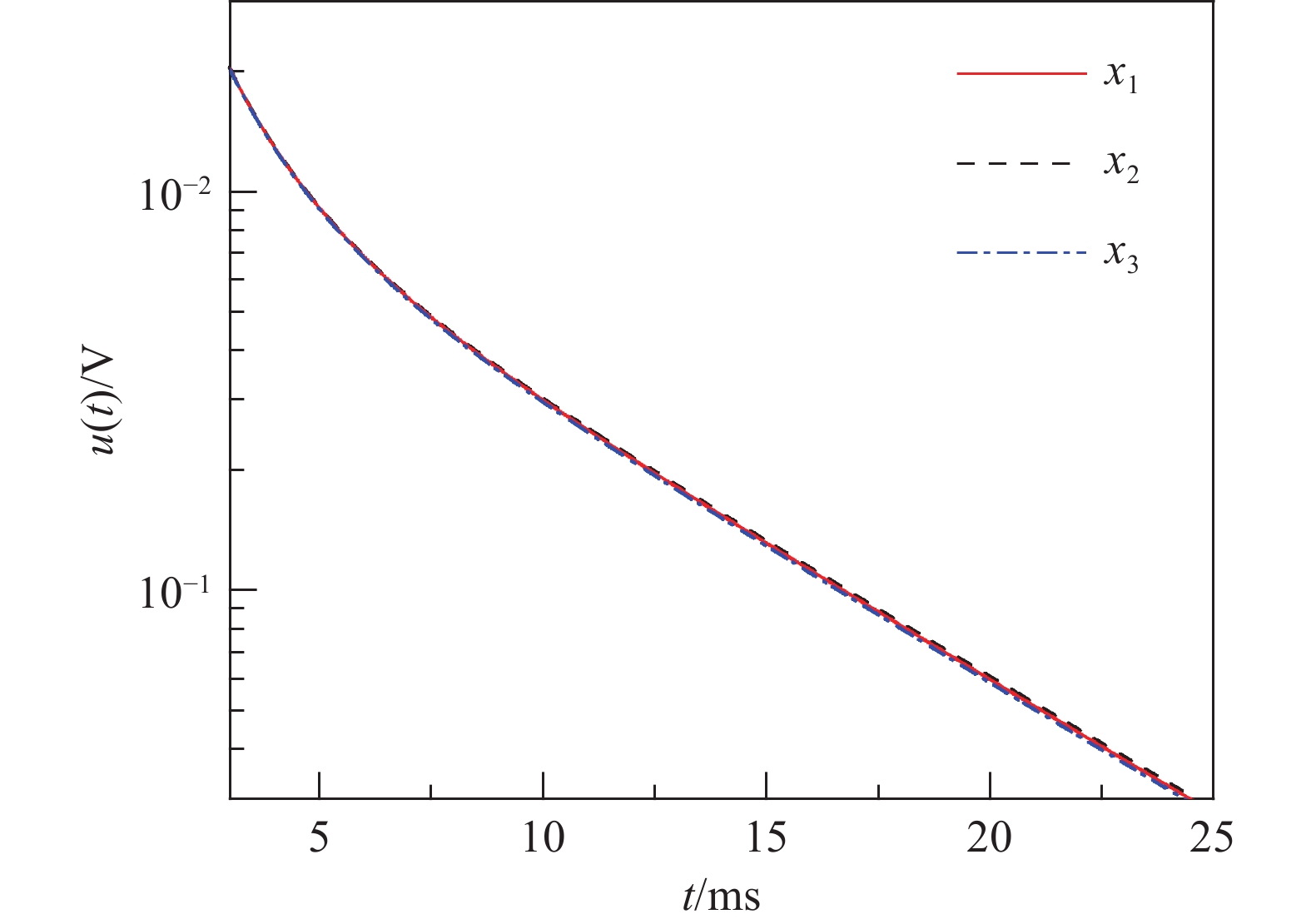
$$ {u_{{\mathrm{ec}}}}\left( {d,\sigma ,{\mu _{\text{r}}},t} \right) = {u_{{\mathrm{ec}}{\text{p}}}}\left( {\sigma d,{\mu _{\text{r}}}d,t} \right) $$ (7) 这表明时域感应电压$ {u_{{\mathrm{ec}}}}(\sigma ,{u_{\mathrm{r}}},d,t) $可以用1个只含变量$ \sigma d $、$ {u_{\mathrm{r}}}d $的函数$ {u_{{\mathrm{ecp}}}} $表出。设参数向量$ {x_{\mathrm{P}}} = {(\sigma d,{u_{\mathrm{r}}}d)^T} $，即时域感应电压$ {u_{{\mathrm{ec}}}}(x,t) $可用$ {u_{{\mathrm{ecp}}}}(x,t) $来表示。为了验证这一结论，将图1所示管道检测模型中，铁磁管道的参数$ x $分别设为：
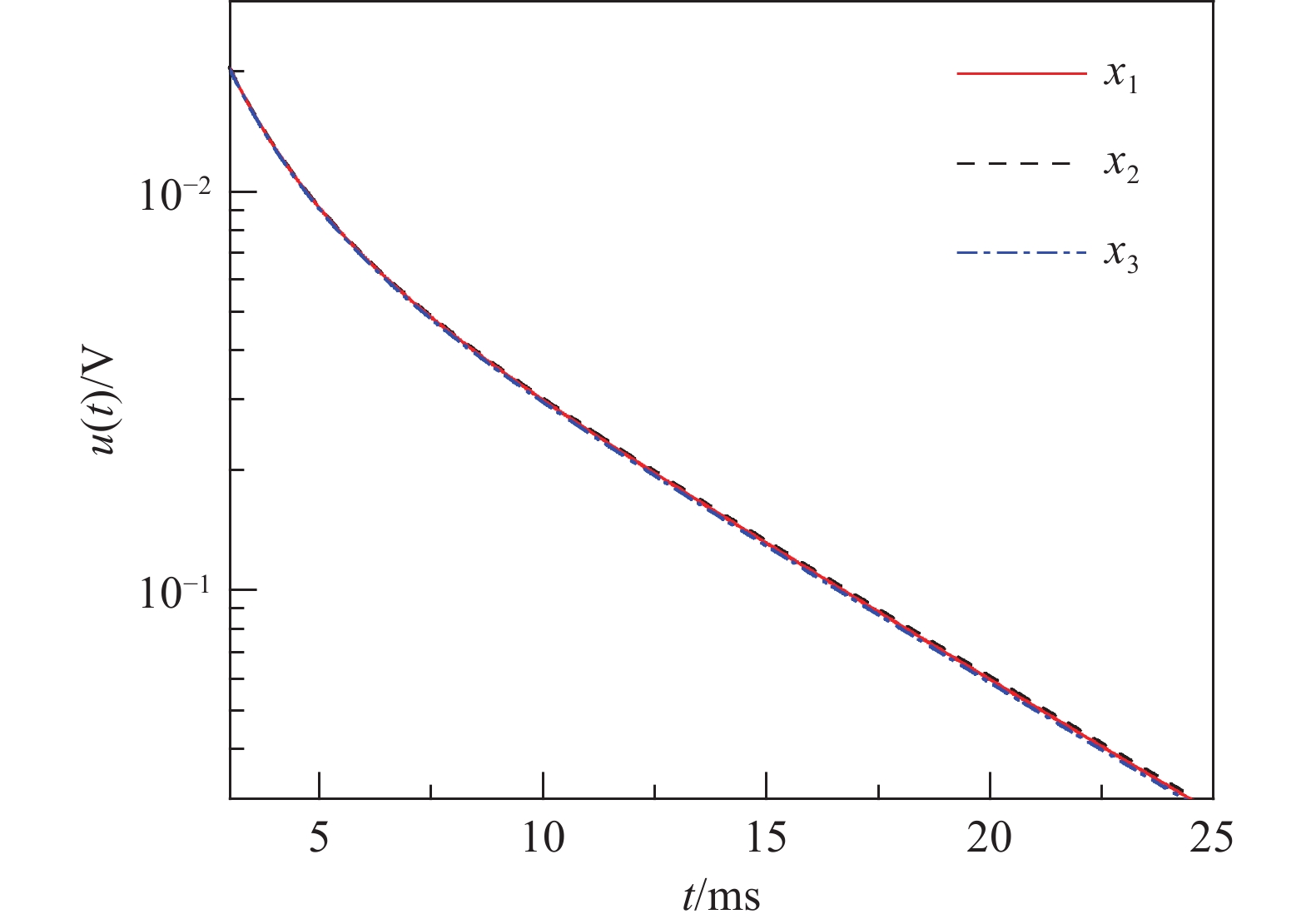
$$ {x_1} = {(7.0mm,4.5M_{\mathrm{s}}/m,200)^T} $$ $$ {x_2} = {(5.0mm,6.3M_{\mathrm{s}}/m,280)^T} $$ $$ {x_2} = {(9.0mm,3.5M_{\mathrm{s}}/m,156)^T} $$ $ {x_1} $、$ {x_2} $和$ {x_3} $对应的$ {x_{\text{p}}} = {(3.15 \times 104S,1.4m)^T} $固定不变。由式（1）分别计算出$ {x_1} $、$ {x_2} $和$ {x_3} $对应的感应电压理论曲线如图2所示。图中感应电压曲线几乎重合，很难区分。综上所述，对铁磁管道实施脉冲涡流检测时，电导率与壁厚以及相对磁导率与壁厚，也会以乘积的形式耦合在一起。
Figure 2. Theoretical calculation curve of time domain induced voltage of ferromagnetic pipeline under different parameter settings
-
研究表明，当参数之间存在耦合关系时，对参数的涡流检测灵敏度会显著降低[18]。当待反演的参数之间存在耦合关系时，参数反演问题会变成1个多解问题，此时，检测信号微小的扰动，或者反演条件（反演算法、迭代初值、迭代次数等）稍微的改变，均会引起检测结果显著的误差，导致参数检测结果的精度和可靠性变差。利用脉冲涡流感应电压检测信号将只能准确反演出$ ud $和$ {u_{\mathrm{r}}}d $两个乘积量，即参数向量$ {x_{\mathrm{p}}} $。一般而言，被检铁磁构件的电磁参数很难预先测得。在实施检测过程中，可设同一段被检构件的电导率为一固定常数，通过两处检测点壁厚反演结果作比，来消除电导率的影响，从而检测出两检测点壁厚的相对变化量。具体检测步骤如下：
步骤1：在待检部件上任意选取一处检测点，标记为参考点$ {Q_0} $，参考点$ {Q_0} $处的真实壁厚记为$ {d_0} $。
步骤2：将线圈探头置于参考点$ {Q_0} $处，对参考点$ {Q_0} $实施脉冲涡流检测，采集得到检测线圈两端时域感应电压$ ({t_1},{u_1}),({t_2},{u_2}) \cdots \cdots ({t_m},{u_m}) $。
步骤3：利用参考点$ {Q_0} $处的时域感应电压测量值$ {u_m} $与式（2）得到的理论计算值$ u(x,t) $比较，建立最小二乘参数反演问题（4），并将参数向量x中电导率值设为常数σ0，壁厚和相对磁导率设为未知参数，然后采用数值迭代算法反演出参考点$ {Q_0} $处壁厚反演结果$ d_0^* $，相对磁导率反演结果$ u_{{\mathrm{r}}0}^* $。
步骤4：在待检部件检测点$ {Q_{\mathrm{j}}} $处放置空心线圈探头，重复步骤2和步骤3，得到检测点$ {Q_{\mathrm{j}}} $处壁厚反演结果$ d_{\mathrm{j}}^* $，电磁参数反演结果$ u_{{\text{rj}}}^* $，检测点$ {Q_{\mathrm{j}}} $处的真实壁厚记为$ {{\text{d}}_{\mathrm{j}}} $。
步骤5：对比参考点与检测点所得结果，得到式（8）：
$$ \frac{{{d_{\mathrm{j}}}}}{{{d_0}}} = \frac{{d_{\mathrm{j}}^ * }}{{d_0^ * }} $$ (8) -
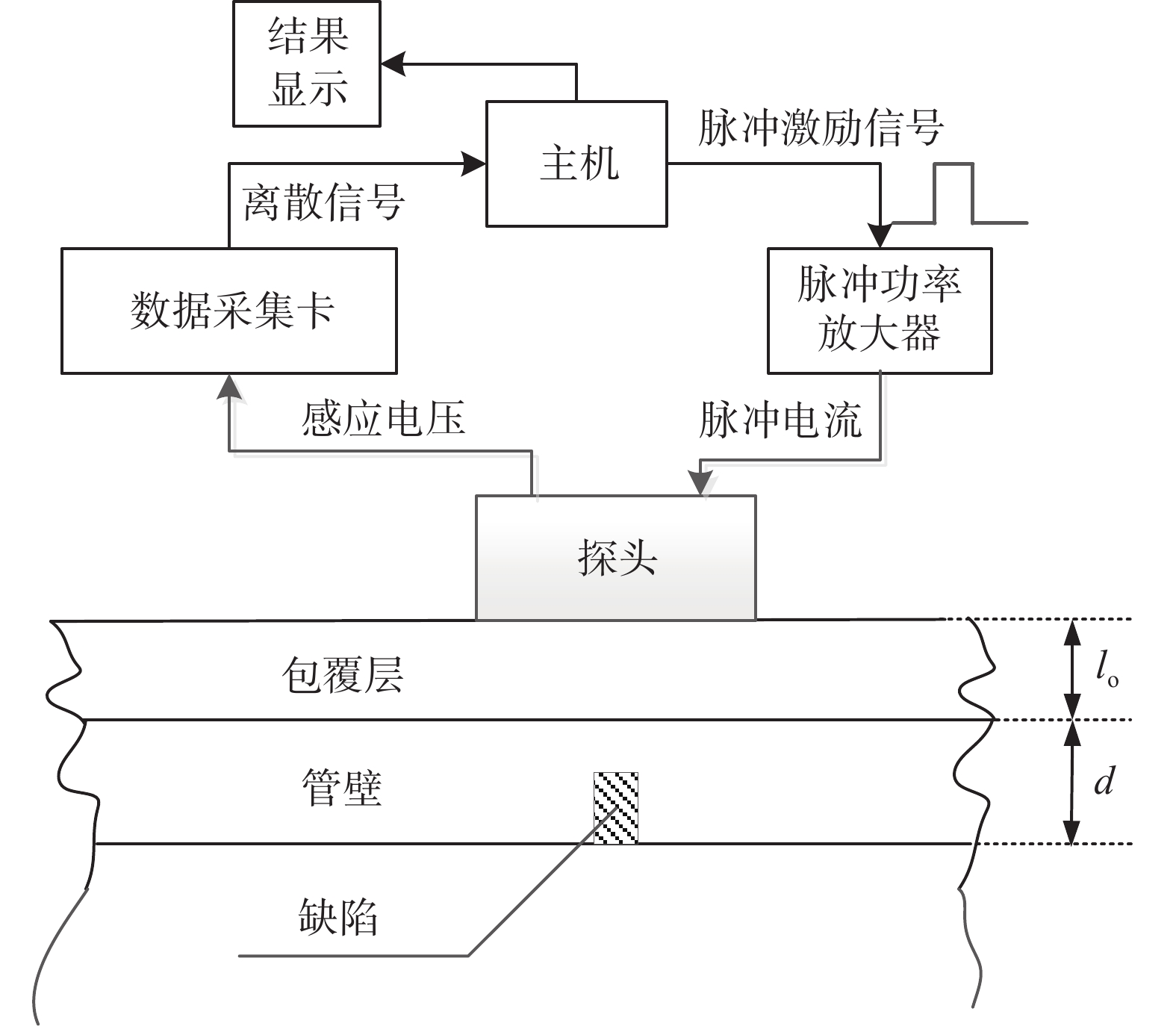
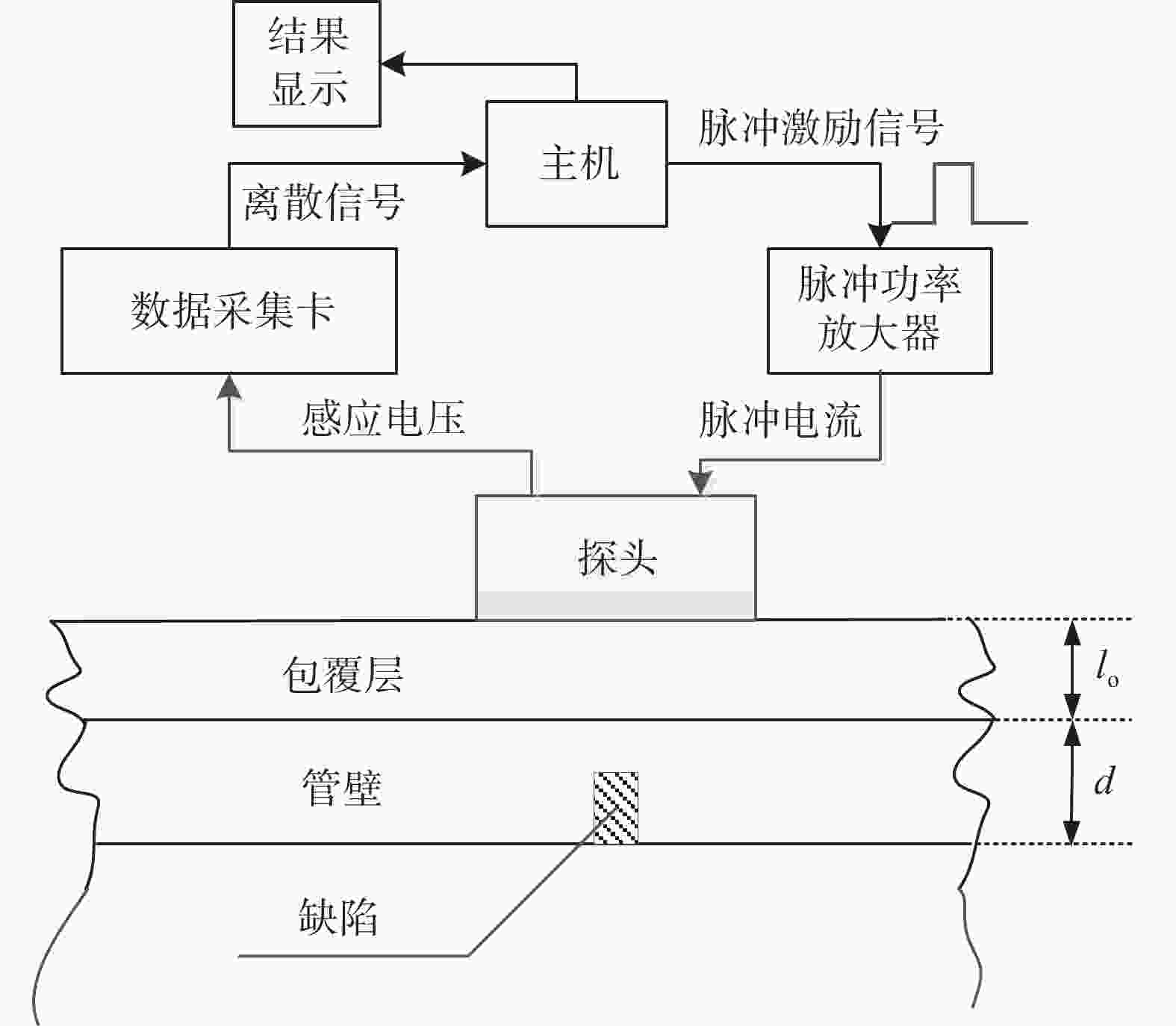
脉冲涡流检测系统的构成如图3所示，通常分为：供电电源部分、脉冲涡流检测探头、数据采集卡、系统主机。系统主机用于脉冲激励信号波形的编辑和输出、探头检测装置两端感应电压的采集和储存、检测信号的后期处理，最终输出检测结果；脉冲功率放大器将主机输出的脉冲激励信号放大成相同波形的大功率脉冲电流输出到激励线圈，在被测构件中产生涡流。探头内部分为激励线圈和检测接收元件两部分，分别用于脉冲磁场的激励和脉冲涡流场的检测，将涡流场的衰减变化转变为检测元件输出端的电压信号随时间的变化。
Figure 3. Schematic diagram of pulse eddy current testing system
-
核电厂二回路汽水管道多采用碳钢或低合金钢制造，管道内径通常为25.4~800 mm，壁厚通常为3.4~80 mm。管线中存在弯头、变径、三通、节流孔板、阀门等结构形状变化显著且易发生湍流的部位，从而引起流体加速腐蚀（FAC）、液滴冲击（LDI）、汽蚀等。由于管材材质、服役环境、结构形状等因素的影响导致管线在敏感部位发生局部减薄[19-21]。
相对于直管而言，弯管检测难度有所增加：（1）弯头部分由于制造原因使得不同位置厚度变化较大；（2）带包覆层的弯头由于曲率原因，会造成不同位置包覆层厚度不均匀的状况，引起提离变化；（3）对于管径较小的弯管导致检测探头无法放置或提力度过大等情况。本文选取核电在役弯管作为研究对象，所得结果更加具有说服力，更能体现本文所提脉冲涡流方法检测的准确性。
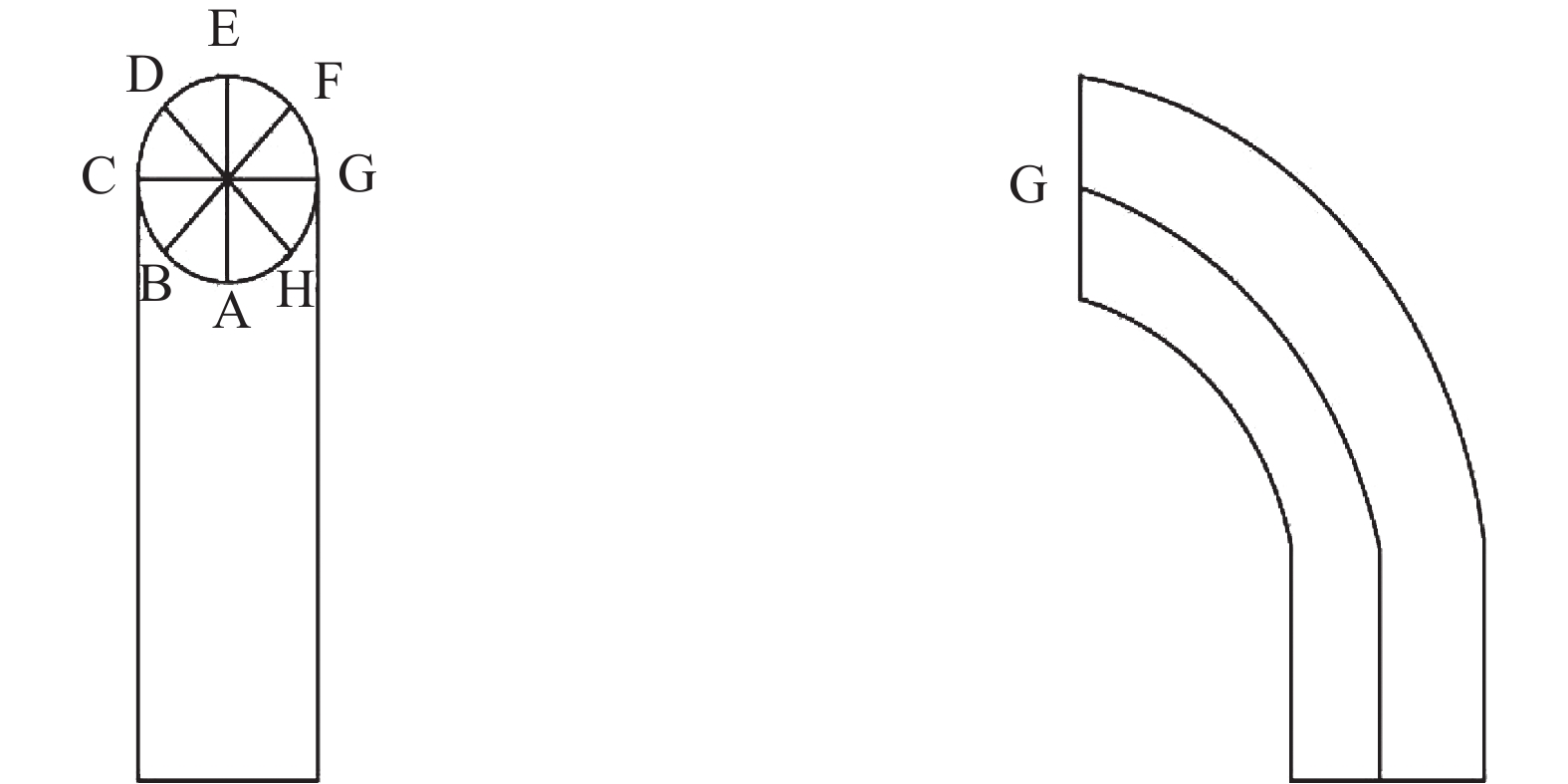
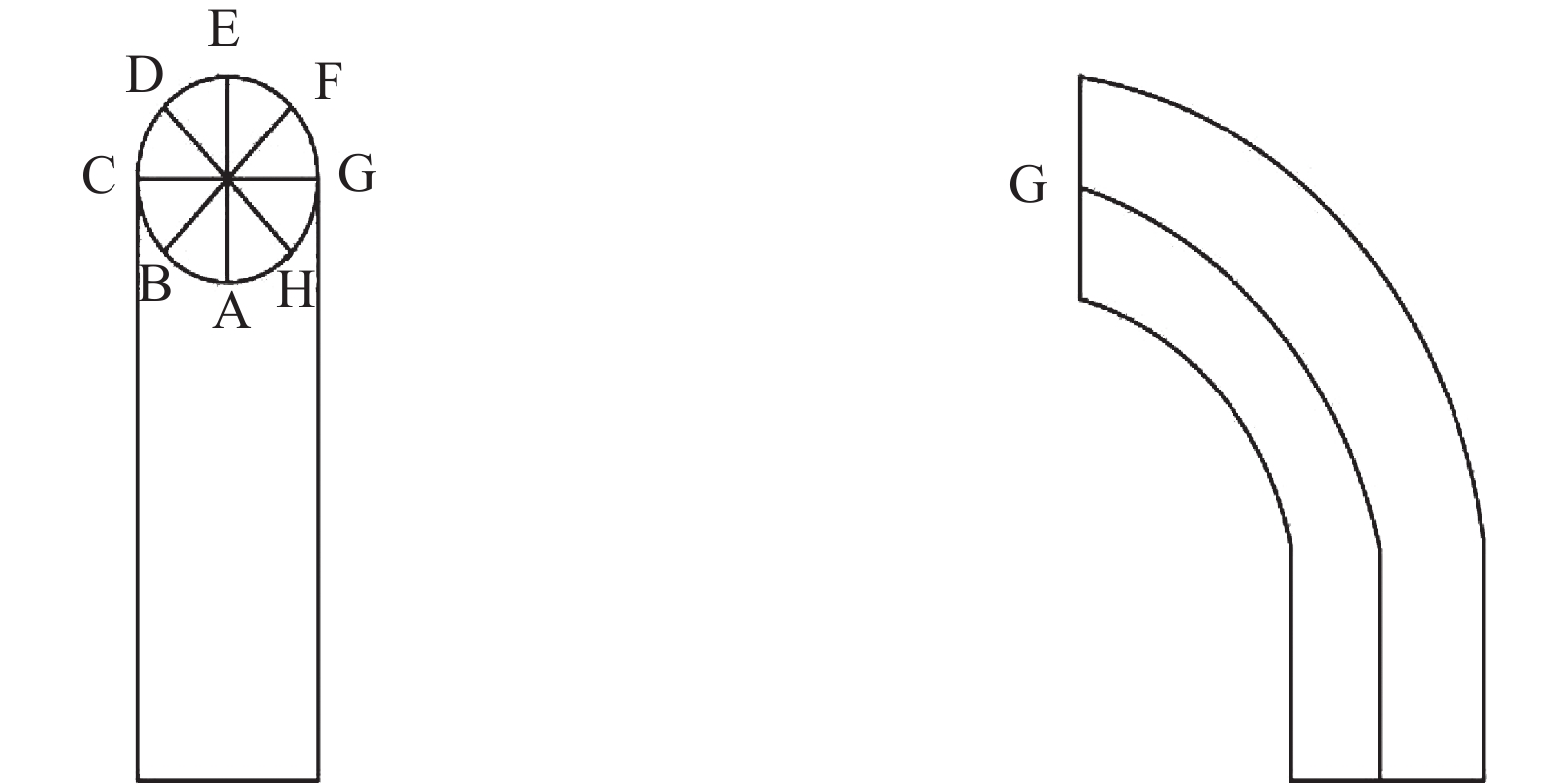
选取7根典型汽水系统弯管作为研究对象，弯管信息如表2所示，将弯管待检区域沿周向划分八条检测线，如图4所示；每条侧线上等距离选取4~10个测点，利用脉冲涡流与常规超声分别对上述测点进行检测。
管线号 外径/mm 名义壁厚/mm 材质 包覆层材质 AHP 559 28 碳钢 铝皮 STR 114 7 碳钢 APA 324 16 碳钢 GSS 114 10 碳钢 GSS 168 9 碳钢 GSS 324 11 碳钢 GSS 324 10 碳钢 Table 2. Subject information
Figure 4. Schematic diagram of test area division
脉冲涡流采用两种记录方法，其中1种以实际壁厚进行标定，如表3所示；另1种采用壁厚变化量进行标定，如表4所示。表3中，背弧侧脉冲涡流数据与超声测厚数据的相对平均误差为9.6%，背弧面两侧D、F线相对平均误差均为11%；表4以C2处进行脉冲涡流标定，记录了各个位置的相对壁厚变化量，壁厚整体变化趋势与超声检测壁厚变化趋势一致。
编号 方法 1 2 3 4 5 6 7 B P 10.56 10.99 11.22 11.44 － － － U 9.60 10.30 11.10 10.80 － － － C P 9.40 10.09 10.06 10.29 10.00 9.64 9.98 U 10.20 11.02 11.00 11.10 11.10 10.80 10.00 D P 9.81 9.84 9.59 9.46 9.24 9.25 9.14 U 10.80 10.70 10.90 10.80 10.40 10.40 10.30 E P 9.98 9.83 9.51 9.35 9.14 － － U 10.90 10.30 10.20 10.70 10.30 － － F P 9.99 10.02 9.73 9.48 9.32 － － U 11.30 11.10 11.00 10.70 10.20 － － G P 9.68 9.95 10.04 10.15 9.75 9.90 － U 11.10 11.50 11.70 11.50 11.40 11.30 － H P 10.08 10.63 10.90 10.61 10.48 － － U 11.60 11.50 11.80 11.30 10.30 － － 注：A线为弯管内弧侧；E线为弯管外弧侧；P为PECT；U为UT。 Table 3. Comparison of pulsed eddy current and ultrasonic test results (actual wall thickness measurement)
编号 方法 1 2 3 4 5 6 7 B PECT 98.3 106.3 103.0 98.4 － － － C 98.3 99.8 99.4 99.7 98.7 98.8 97.2 D 93.5 98.3 96.6 98.7 97.5 99.3 87.9 E 93.7 91.4 91.5 89.4 87.9 － － F 97.5 99.1 99.5 98.4 97.7 － － G 97.9 97.4 101.5 101.5 101.2 99.8 － H 96.9 99.0 102.2 100.2 － － － 注：每个测点记录的为壁厚百分比%；PECT为脉冲涡流检测。 Table 4. Relative wall thickness measurement
选取实验对象2进行测试，脉冲涡流以10 mm进行标定。选取实验对象2进行测试，脉冲涡流以7 mm进行标定。选取实验对象3进行测试，脉冲涡流以22 mm进行标定。两种方法对比结果如表5所示。
编号 方法 1 2 3 4 5 6 7 8 9 B U 22.10 22.56 22.18 22.84 － － － － － P 21.10 21.70 22.80 22.70 － － － － － C U 21.43 21.88 22.34 21.24 22.47 21.69 22.38 － － P 20.40 21.80 22.10 22.40 22.20 22.50 22.20 － － D U 22.06 21.84 22.33 21.68 21.57 21.56 22.01 22.42 － P 21.80 21.80 21.80 22.30 21.70 21.80 21.90 21.80 － E U 22.75 22.06 21.49 21.26 21.24 21.85 21.44 22.11 22.92 P 21.80 21.50 21.80 21.90 21.30 21.20 21.80 21.70 21.90 F U 22.99 22.55 22.54 22.63 22.41 22.12 22.31 － － P 21.40 21.70 22.20 22.40 21.80 21.80 22.40 － － G U 22.57 22.30 22.37 22.90 － － － － － P 21.50 21.60 21.80 21.30 － － － － － Table 5. Result comparison of two methods
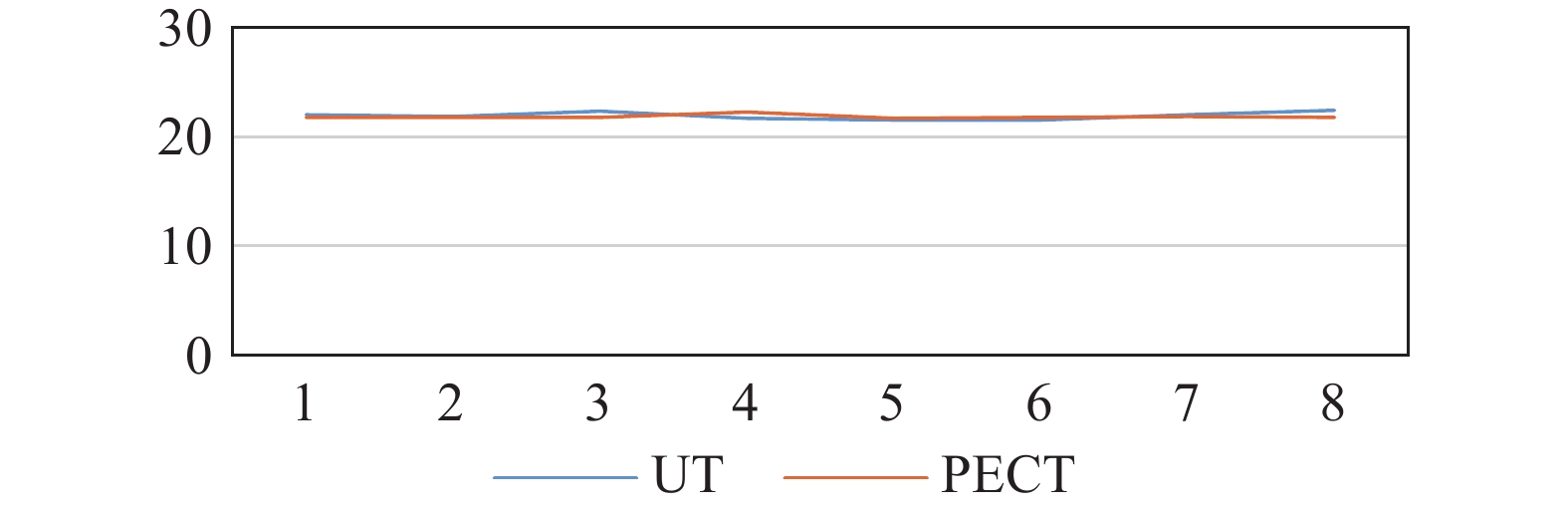
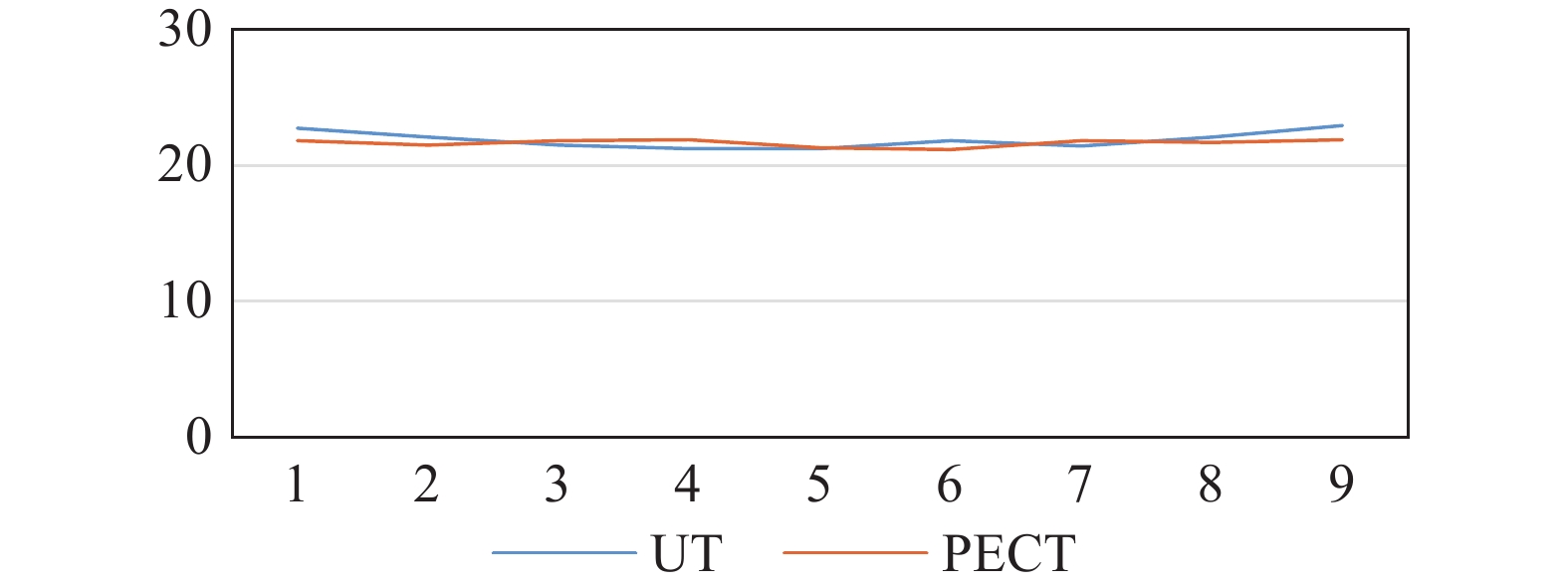
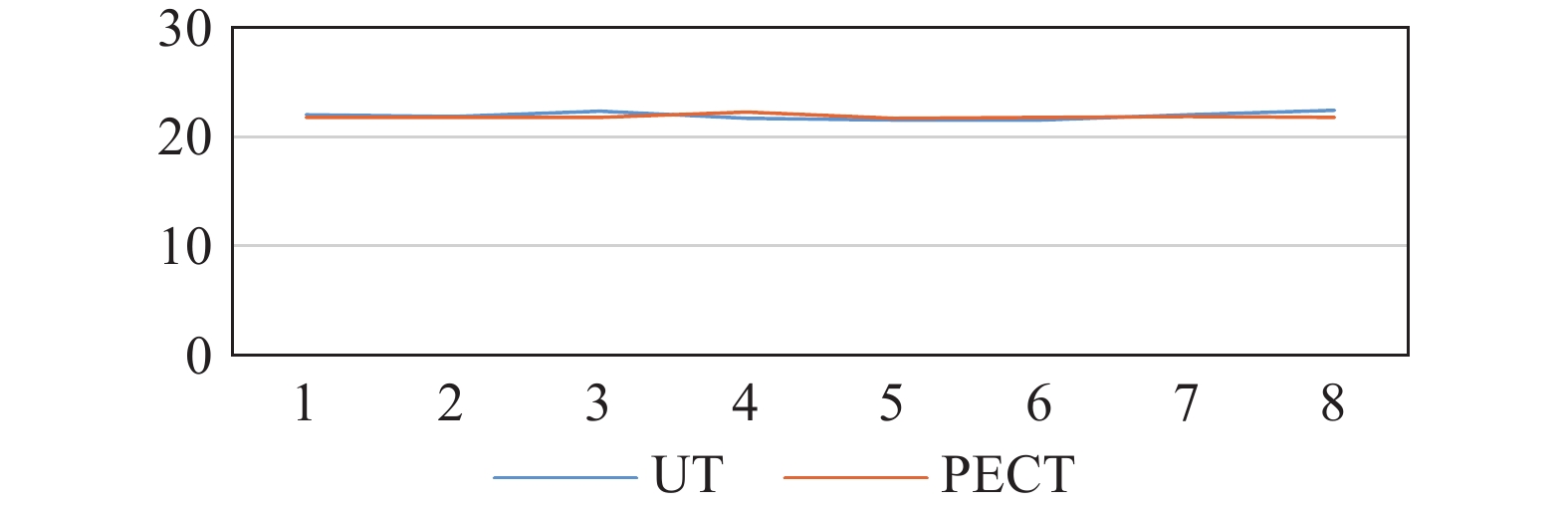
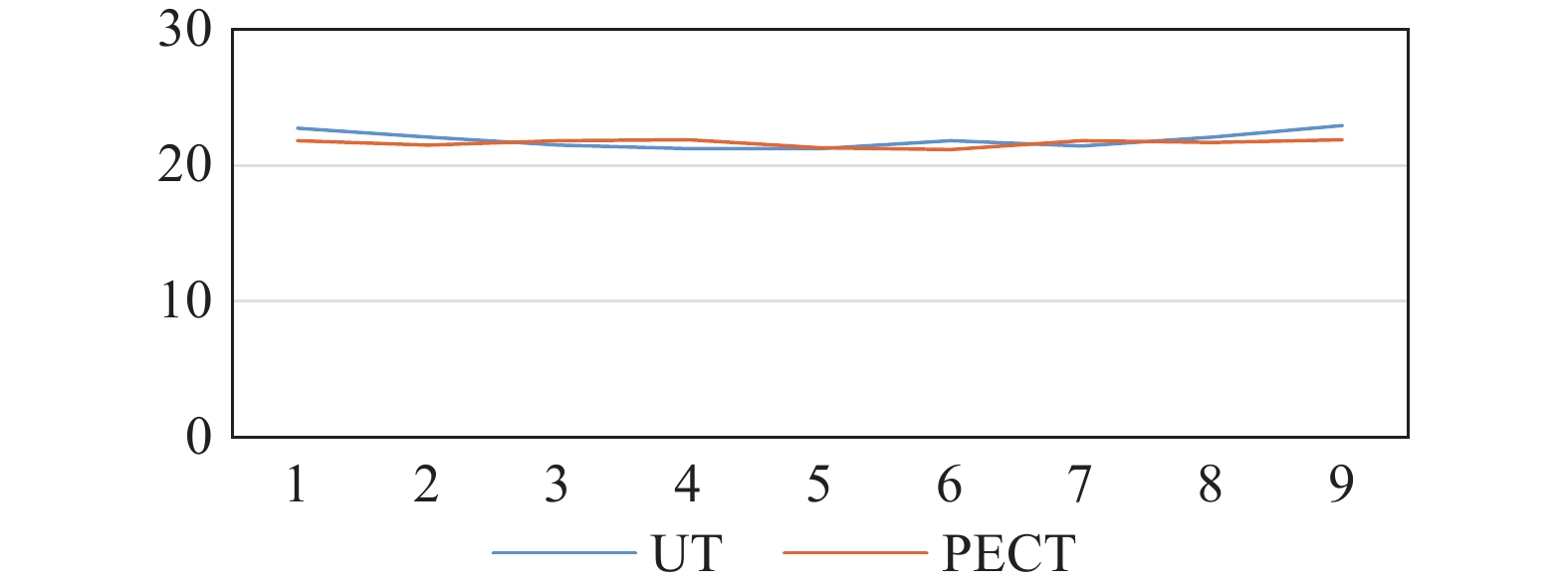
D线和E线结果对比线如图5、图6所示。弯头背弧侧通常是易减薄区域，选取背弧面的3条检测线（D、E、F）作为主要参考，通过测试线上两种方法所得数据对比，可以反映出脉冲涡流技术的适用性。E线上最大误差为4.1%，最小误差为0.2%，平均误差为2.5%；D、F线平均误差分别为1.5%、2.5%。
Figure 5. Result comparison curve of D line
Figure 6. Result comparison curve of E line
选取实验对象1进行测试，脉冲涡流以28 mm进行标定。从表6中可以得出，同一条检测线上脉冲涡流检测数据整体平稳，与超声测厚结果误差较小，具体为：C线上两种方法所得数据相对平均误差为1%，背弧侧（E线）为2.8%，整体差异较小。
编号 方法 1 2 3 4 5 6 7 8 9 A U 37.47 38.98 40.25 39.24 39.88 39.31 36.43 － － P 37.13 37.39 38.32 37.53 37.26 37.66 37.79 － － B U 36.65 36.31 36.54 38.00 36.44 37.12 36.74 37.35 37.18 P 36.51 36.38 36.70 37.29 36.90 36.90 36.30 37.29 36.64 C U 36.59 35.71 33.70 32.04 32.00 32.22 32.97 32.37 － P 36.51 32.80 32.80 32.80 31.20 33.15 32.57 31.31 － D U 35.50 35.65 35.83 36.71 35.48 35.33 35.28 36.12 36.97 P 34.71 35.49 35.87 37.15 36.20 36.64 36.62 36.25 35.35 E U 37.47 38.98 40.25 39.24 39.88 39.31 36.43 － － P 37.13 37.39 38.32 37.53 37.26 37.66 37.79 － － Table 6. Result of bending test
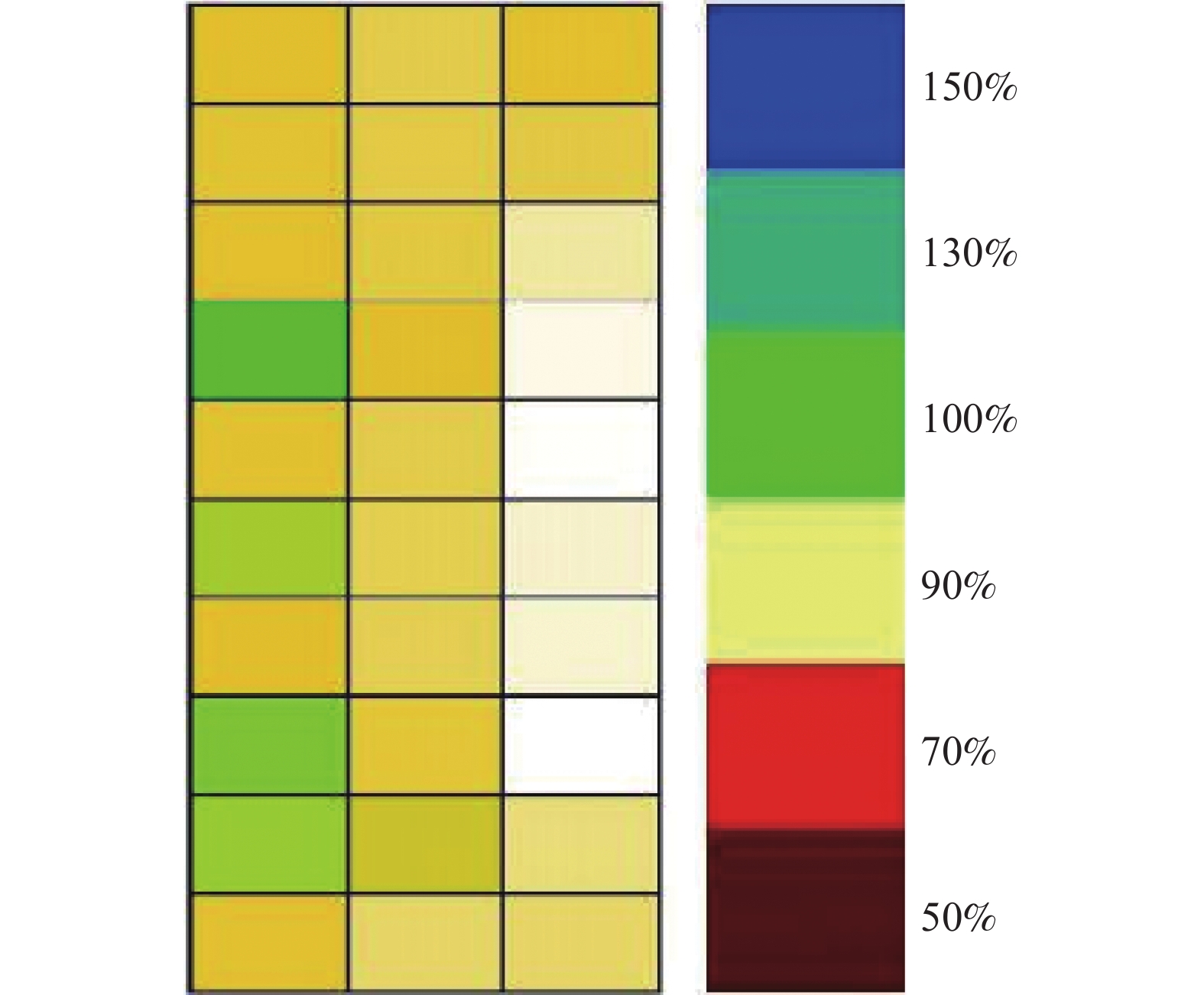
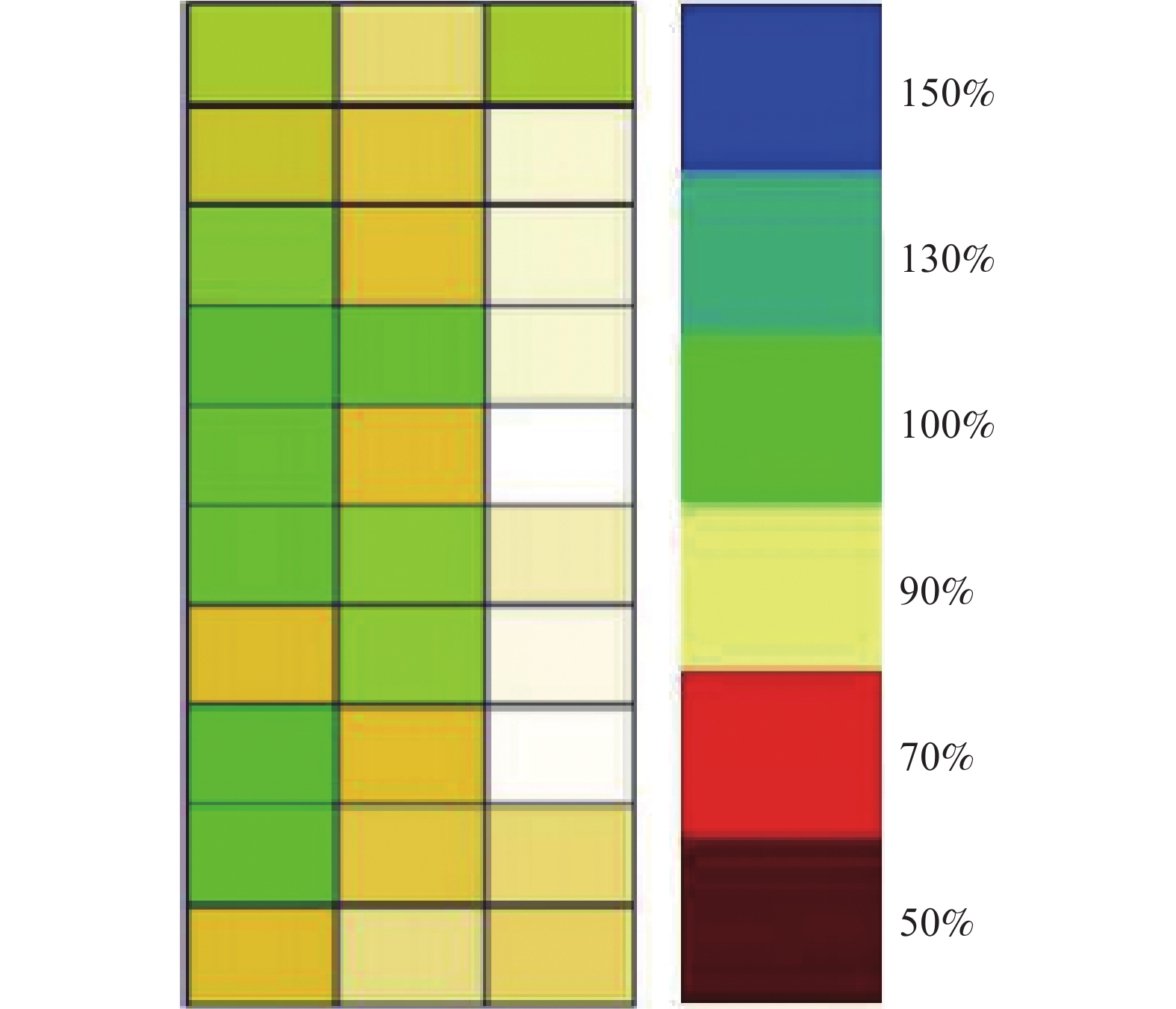
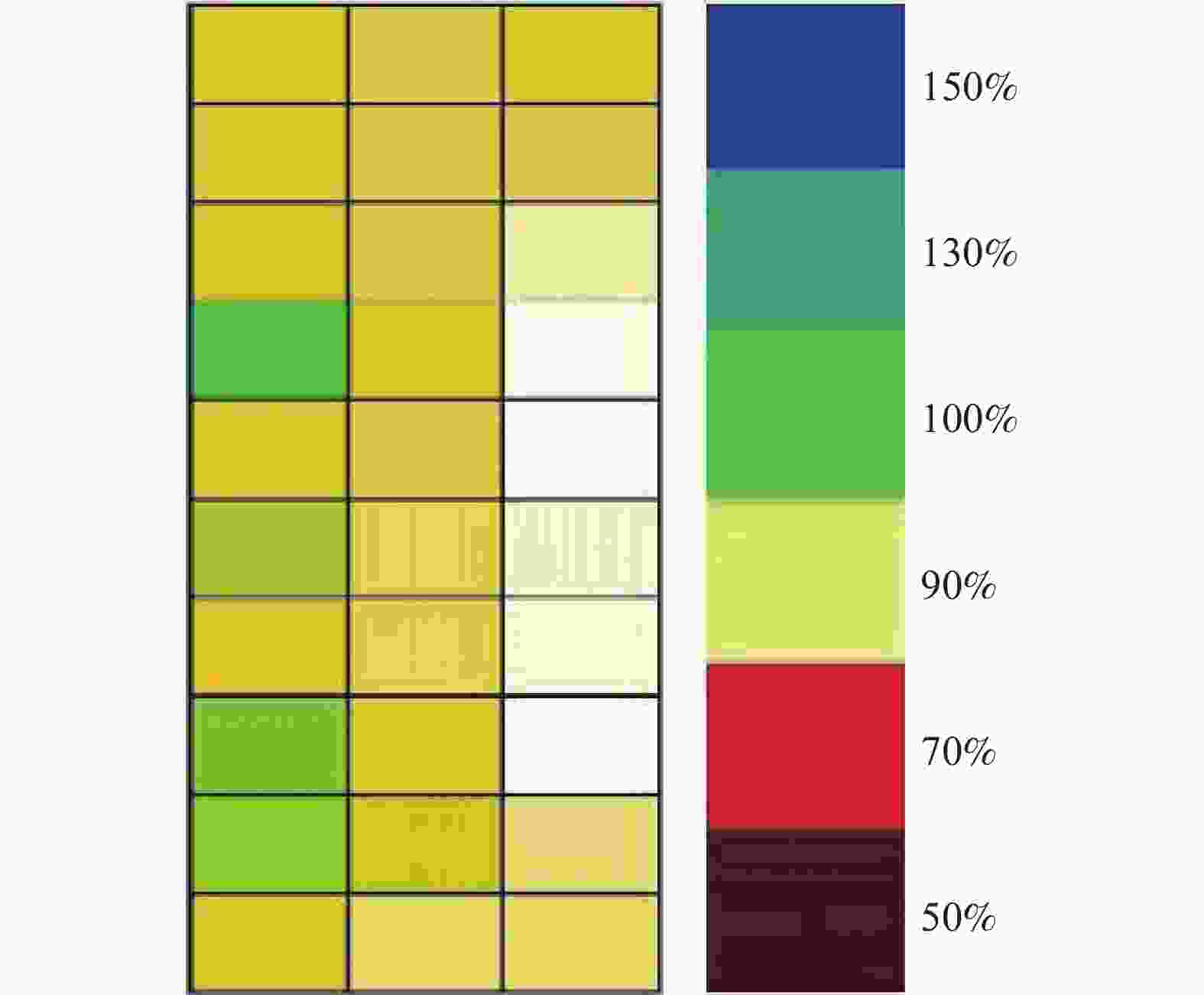
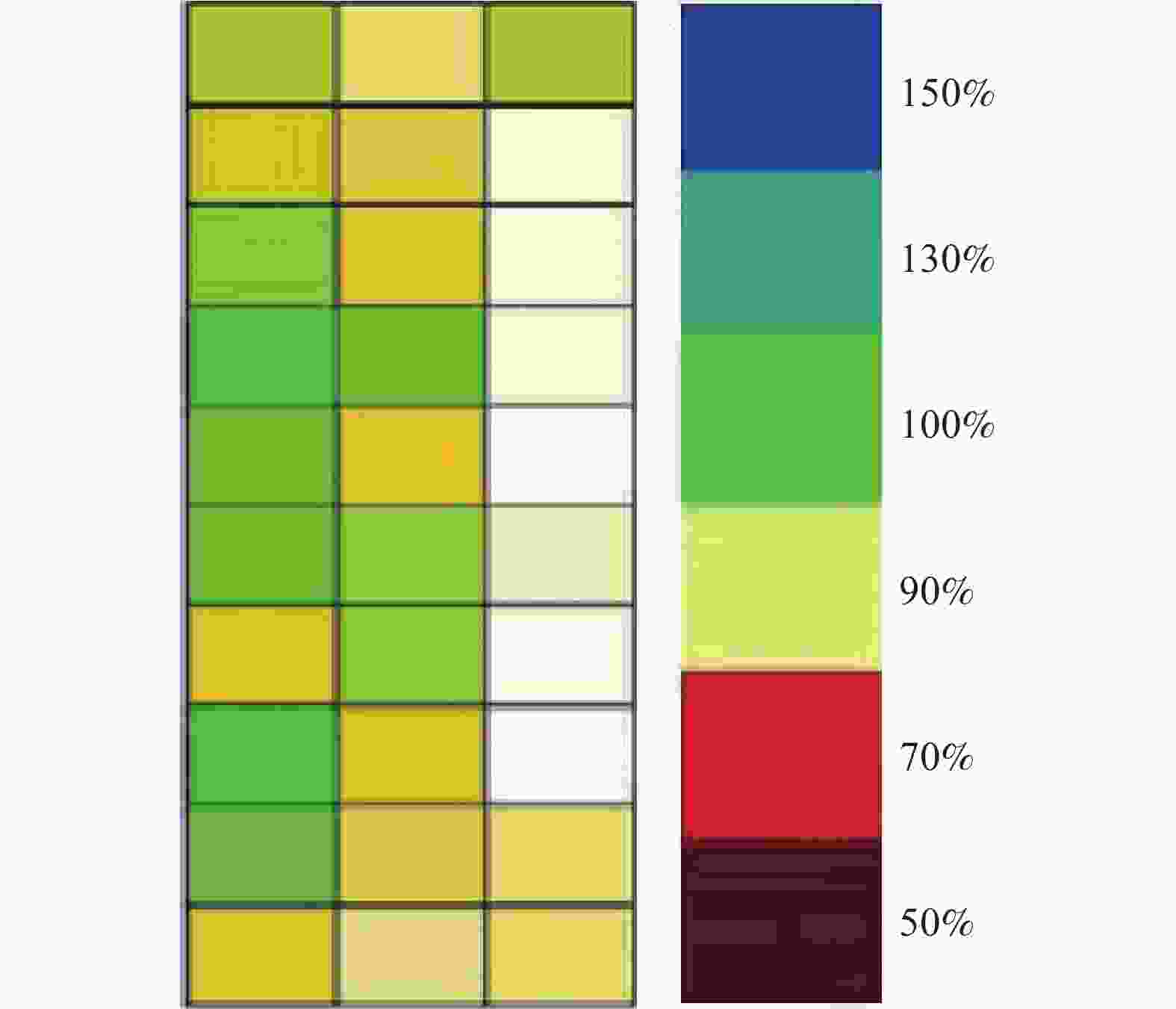
选取D~F线长方形区域，根据各侧线上测点划分网格，对每个网格进行脉冲涡流进行测厚，将结果以伪彩色图进行描述，以颜色变化表示相对壁厚的变化。如图7和图8所示，可以得出相同位置两种方法测量的相对壁厚变化趋势基本一致，这也证明了本文所研究的脉冲涡流技术具有更好的适用性。
Figure 7. Result of pulse eddy current test
Figure 8. Result of ultrasonic test
综上所述，本次共对7根弯管进行测试，总计布置218个测厚点，用“△”表示同一位置上脉冲涡流测厚值相对超声测厚值的相对误差百分比，其中△≤5%的测厚点占52%，5%＜△≤10%的测厚点占22%，△＞10%的测厚点占26%。从占比分析可以得出，存在较大误差的点占比在20%左右，大部分误差较大的点主要集中在弯管测线的首末端，由于弯管两侧存在焊缝，导致端面效应影响脉冲涡流测厚精确度；对于弯管背弧面敏感部位，对比两种方法在E、F线附近的结果，所测结果的相对误差为6%。
-
在铁磁管道脉冲涡流检测中，管道电导率与壁厚以及相对磁导率与壁厚会以乘积形式耦合在一起，利用感应电压信号，只能反演出这两个乘积量。选取同一段管道上两处不同的检测点，实施脉冲涡流检测，将所得结果进行反演及对比，可消除管道材料电磁参数的影响，得到两检测点壁厚的相对变化量。该检测方法一定程度上可有效抑制脉冲激励磁场强度、探头提离变化对壁厚检测结果的影响。选取相同或相近检测条件下的壁厚反演结果作为参考值，可进一步抑制检测条件变化对壁厚检测结果的影响，提高壁厚检测的可靠性。利用本文提出的铁磁管道壁厚脉冲涡流检测方法对在役管道非焊缝处进行扫描检测并于超声测厚结果对比，检测结果准确、可靠，对于如何解决弯管焊缝引起的端面效应，则是未来脉冲涡流技术的主要发展方向。
Application of Pulsed Eddy Current Detection in Pipeline of Nuclear Power Plant
doi: 10.16516/j.ceec.2024.4.12
- Received Date: 2023-05-06
- Rev Recd Date: 2023-09-08
- Available Online: 2024-07-12
- Publish Date: 2024-07-30
-
Key words:
- pulsed eddy current testing /
- ferromagnetic tube /
- wall thickness testing /
- inversion problem /
- corrosion thinning
Abstract:
| Citation: | HAN Yang, ZHU Qi, CHEN Yongan, et al. Application of pulsed eddy current detection in pipeline of nuclear power plant [J]. Southern energy construction, 2024, 11(4): 118-126 doi: 10.16516/j.ceec.2024.4.12
|
DownLoad:
