-
近年来，由于电力需求的增加以及配电网线路受损或电气设备损坏造成漏电等原因，火灾和人身触电事故发生的次数也明显增多[1-2]。因此，电力安全问题已经逐渐引起了人们的广泛关注。为了预防火灾和人身触电事故的发生，用于安全保障的剩余电流保护装置在低压配电网中得到广泛使用。目前广泛运用的剩余电流保护装置其原理是通过判断总剩余电流有效值是否达到额定动作值，来判断线路是否发生触电事故[3-4]。这种剩余电流保护装置极易受到电气环境变化等因素影响而发生误动或拒动，同时也无法识别触电事故的类型[5-6]。
国内外学者针对剩余电流保护装置进行了大量的研究，表明了开发新型剩余电流保护装置的关键技术之一在于提取触电信号的特征进行触电类型识别。用于识别触电类型的特征提取方法常见的有时频域特征分析、小波变换、傅里叶变换和统计特征提取等。文献[7]利用统计相关理论提取了生物触电的时域和频域特征参数，再结合主成分分析法和PSO优化支持向量机实现了对触电故障类型的识别。文献[8]基于小波包变换分析触电剩余电流低频分量能量谱并提取触电特征向量，结合量子神经网络对触电事故类型进行识别，取得了较好的效果。文献[9]基于统计量提取了6个参数作为特征向量，并以人工神经网络为分类器，获得超过85%的放电类型识别率。以上方法的计算过程较为复杂，同时大部分文献只进行理论推导与仿真分析，没有进行具体实验的验证。
神经网络具有收敛速度快、网络结构简单、自学习与自适应性强，以及可利用线性学习能力求解非线性问题等优点[10-12]，被广泛设计并应用于特征识别和模式分类。因此，本文首先对实验得到的触电信号数据进行预处理，并提取了信号波形的时频域特征参数以及波形的二次谐波幅值数据。再利用主成分分析法对特征参数进行降维处理，并结合GRU神经网络建立触电诊断模型。本文方法对新一代剩余电流保护装置的研究与开发提供了新的思路，对提高配电系统供电可靠性也具有参考价值。
-
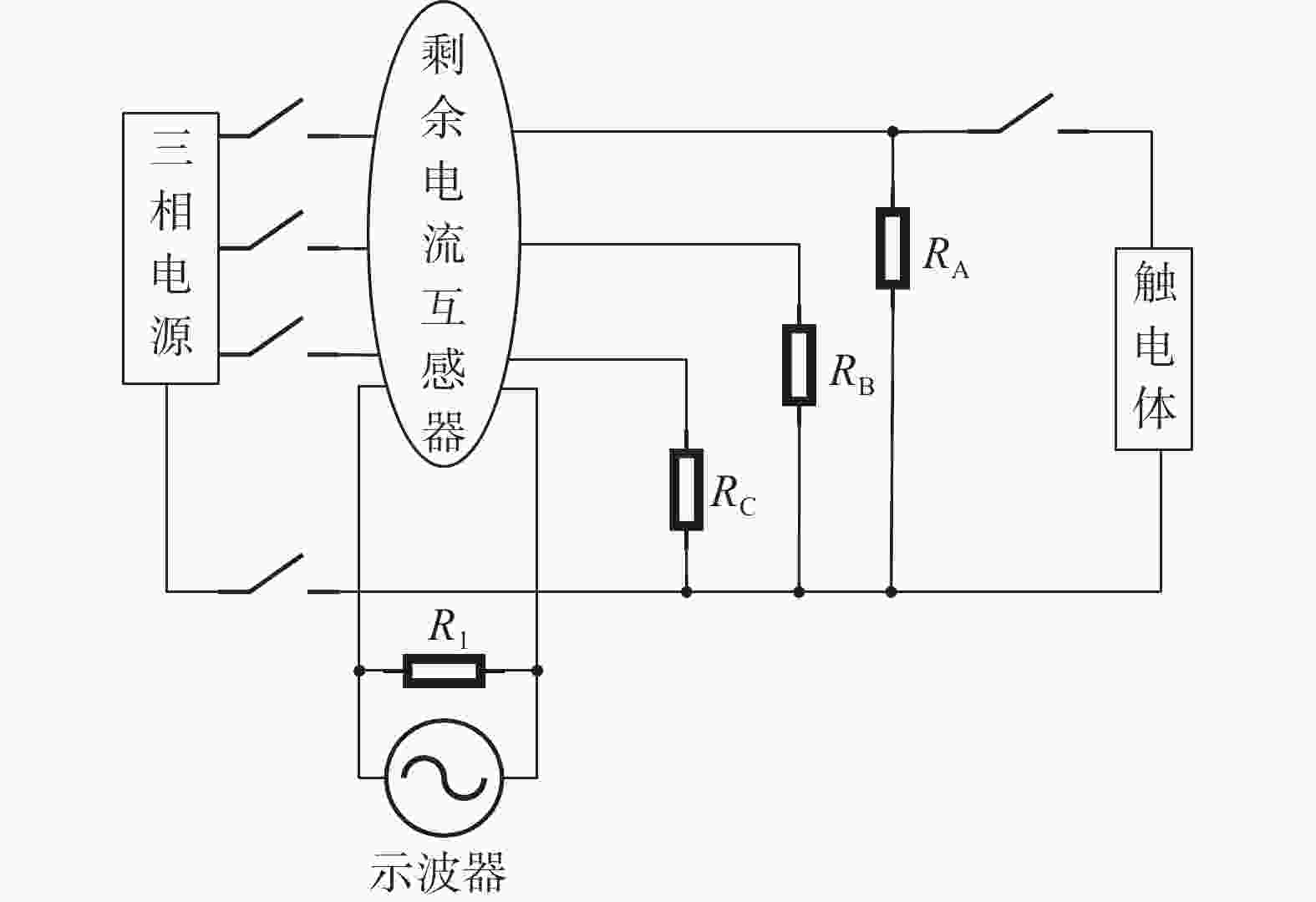
本文使用猪肉作为触电体，实际电路中的三相电阻使用滑动变阻器替代。通过调节三相电阻的电阻值获得三相平衡与三相不平衡触电信号两大类样本，实验原理图如图1所示。
Figure 1. Experimental schematic diagram
图1中RA为A相电阻，RB为B相电阻，RC为C相电阻。剩余电流互感器测量三相总剩余电流。触电体并联于A、B、C相可分别获得不同相的触电信号。
在实验中，取经过隔离开关的三相市电作为实验输入三相电，确保实验过程的安全。A、B和C三相电路的每一相均用三个最大阻值为200 Ω的滑动变阻器替代。R1与剩余电流互感器组成回路，阻值为280 Ω。本文根据实验原理图连接电路，并选择不同类型的猪肉作为触电体进行实验，从而获得更加丰富的样本数据。每次做实验，都是先接通三相回路，再接通触电回路，即模拟触电。为了实验采集数据的可靠性，每次触电实验在相同条件下都进行多次触电并采集数据。
-
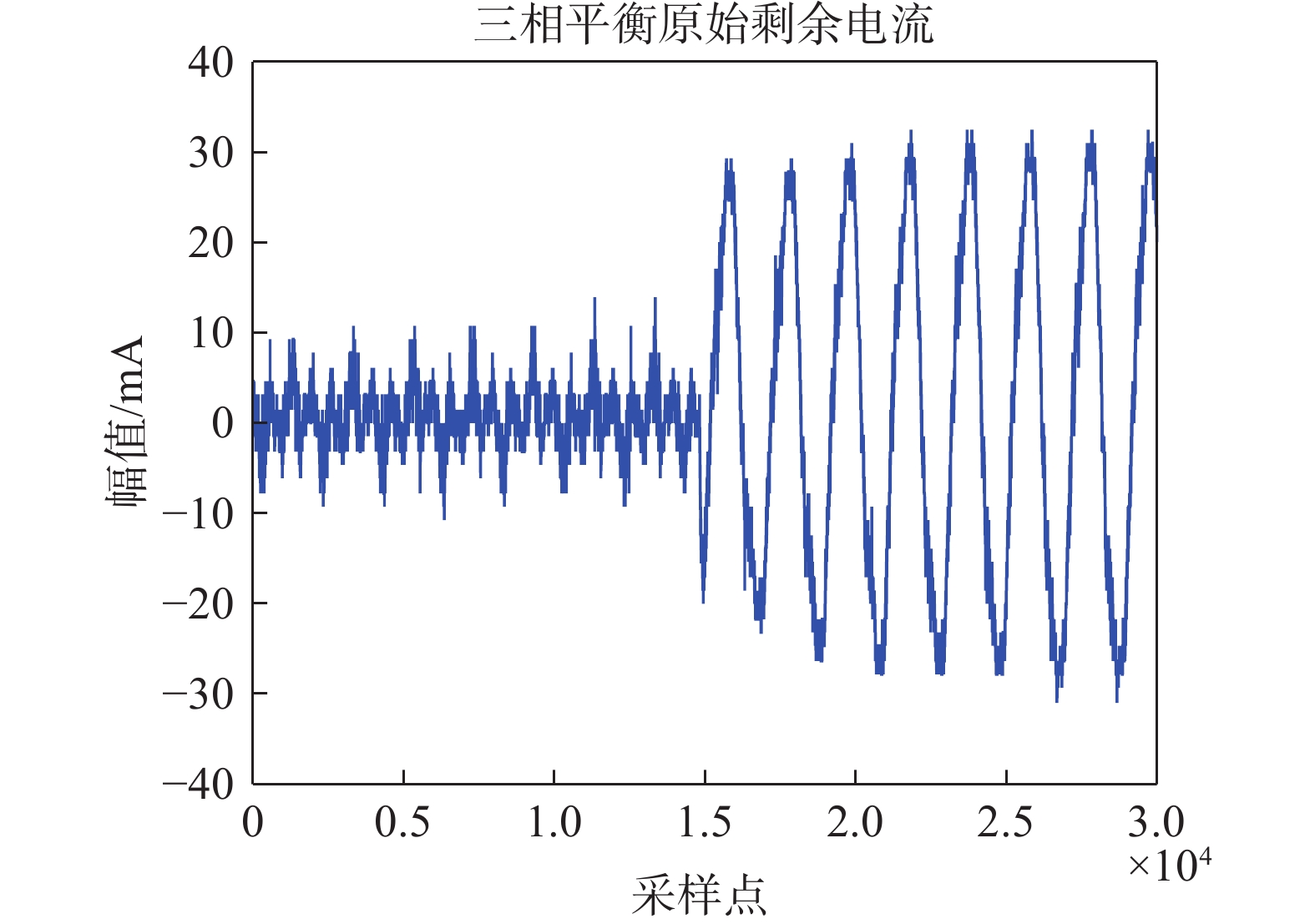
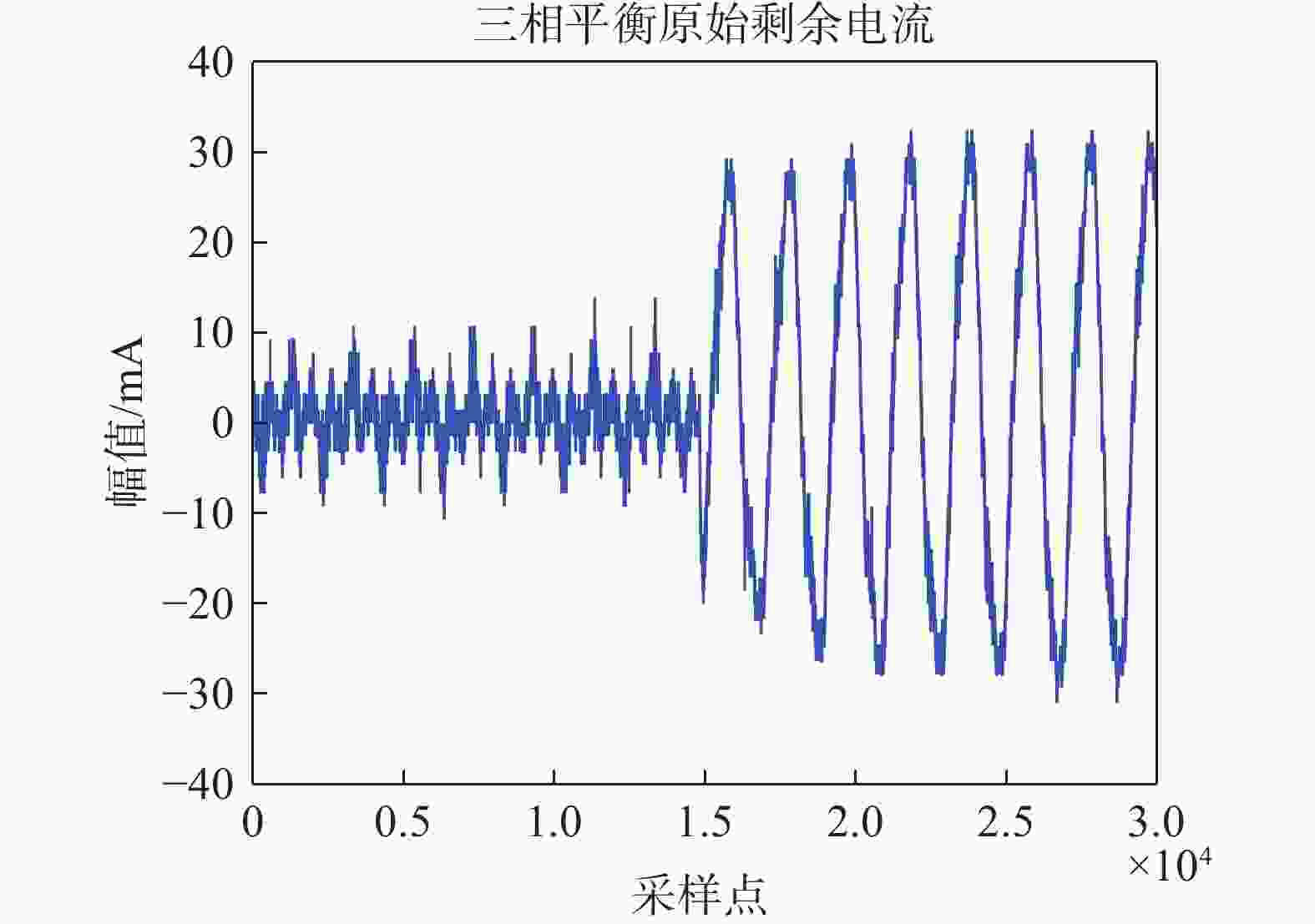
生物体接入电路中可以等效为1个复杂的阻抗网络，而且当发生触电时，等效的阻抗网络参数是时刻在变化的，并且在触电发生的较短时间内电流呈现出1个递增周期函数的趋势[1]。触电信号样本数据均由实验室触电试验平台的示波器采集得到。采集的剩余电流波形频率为100 kHz，1个周期0.02 s的采样点数为2 000。触电原始剩余电流波形如图2所示。
Figure 2. The original residual current signal waveform of electrocution
-
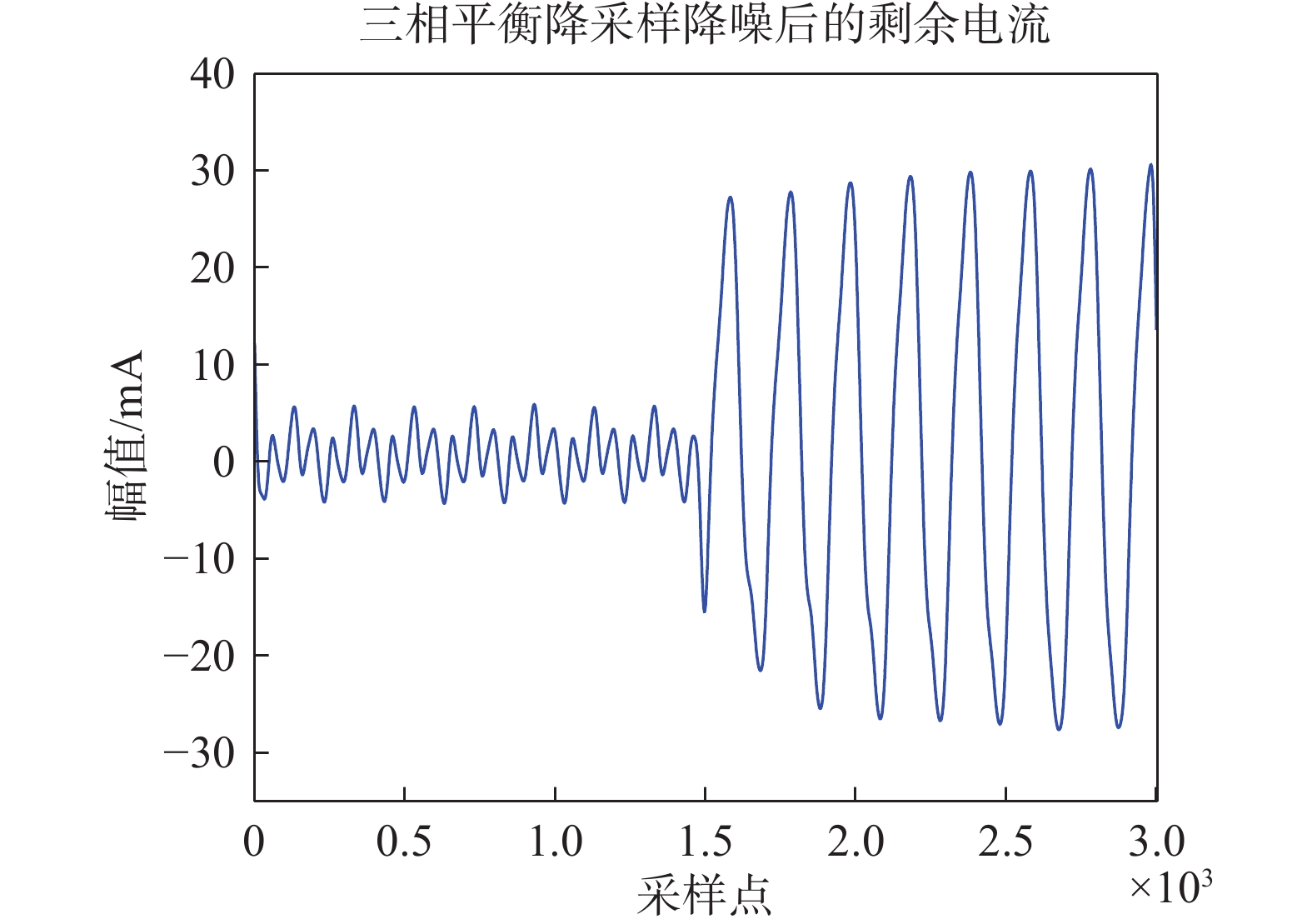
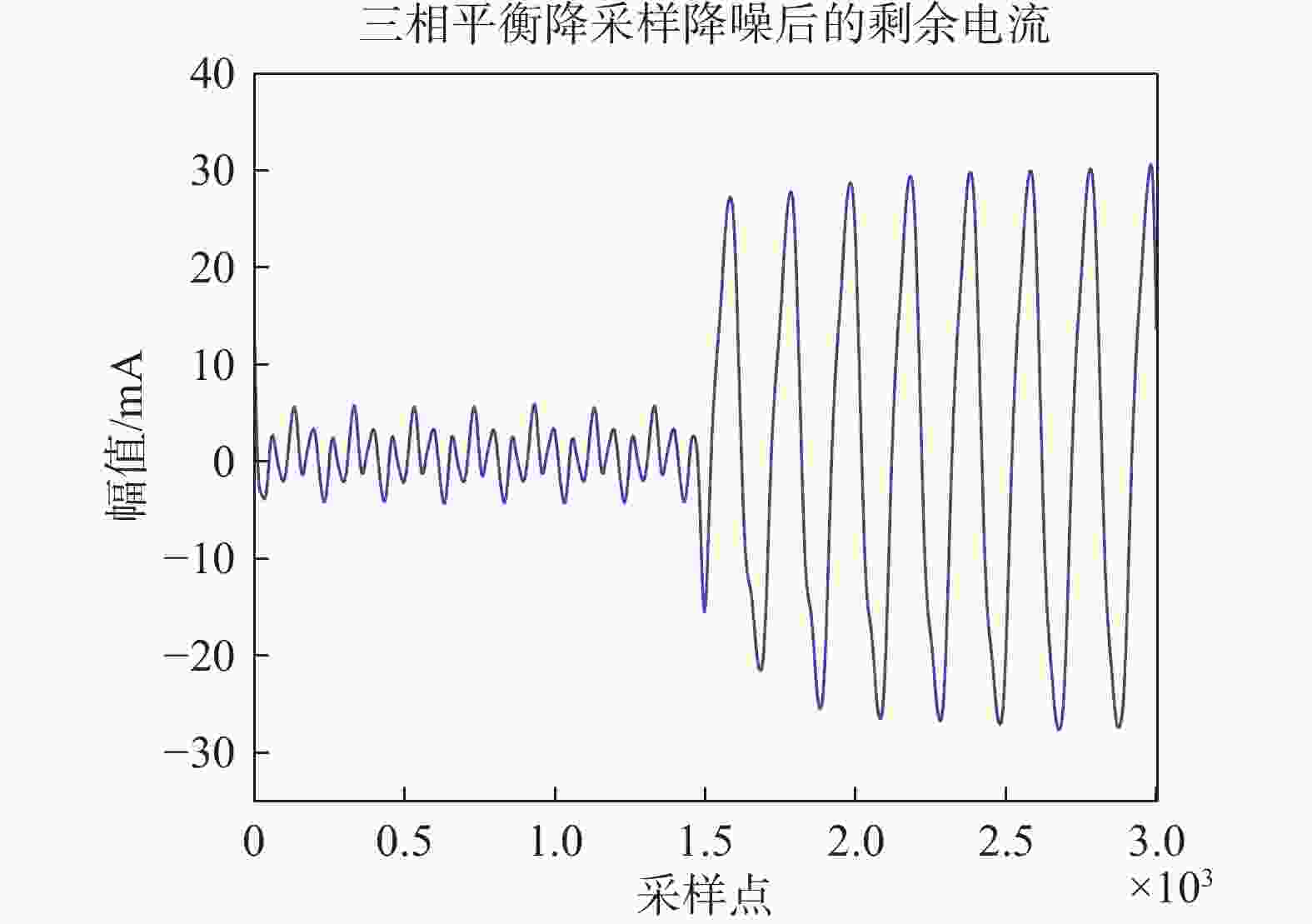
由于示波器的采样频率较高，以及采集原始剩余电流时含有噪声，因此需要对原始剩余电流信号进行处理。首先是降采样处理，将电流波形的频率由100 kHz下降为10 kHz；其次采用了最大重叠离散小波变换（MODWT）对降采样后的数据进行降噪处理。降噪的结果为保存信号的低频分量。降采样和离散小波降噪后的剩余电流波形如图3所示。
Figure 3. Residual current waveform after downsampling and noise reduction
-
由于所采集的触电剩余电流信号包含大量的冗余信息和噪声，难以直接进行识别。因此，需要进行特征提取，从原始的剩余电流信号中提取出对触电类型鉴别有帮助的特征，并将其转化为可用于分类算法的特征向量，以提高分类器的准确性和鲁棒性。
本文采用了滑动窗口法提取触电电流波形的11个时域特征参数，具体的表达式如表1所示。
序号 特征表达式 序号 特征表达式 1 $ {a}_{1}=\dfrac{1}{N}\displaystyle \sum _{i=1}^{N}x\left(i\right) $ 7 $ {a}_{7}={a}_{5}-{a}_{6} $ 2 $ {a}_{2}=\dfrac{1}{N}{\displaystyle \sum _{i=1}^{N}}\left|x\left(i\right)\right| $ 8 $ {a}_{8}=\sqrt{\dfrac{1}{N}{\displaystyle \sum _{i=1}^{N}}{\left|x\left(i\right)\right|}^{2}} $ 3 $ {a}_{3}=\dfrac{1}{N}{\displaystyle \displaystyle \sum _{i=1}^{N}}{\left|x\left(i\right)-{a}_{1}\right|}^{2} $ 9 $ {a}_{9}=\dfrac{\frac{1}{N}{\displaystyle \displaystyle \sum _{i=1}^{N}}{\left|x\left(i\right)-{a}_{1}\right|}^{3}}{{{a}_{4}}^{3}} $ 4 $ {a}_{4}=\sqrt{{a}_{3}} $ 10 $ {a}_{10}=\dfrac{{a}_{8}}{{a}_{2}} $ 5 $ {a}_{5}={\mathrm{max}}\left(x\right(i\left)\right) $ 11 $ {a}_{11}={\displaystyle \sum _{i=1}^{N}}{x\left(i\right)}^{2} $ 6 $ {a}_{6}={\rm{min}}\left(x\right(i\left)\right) $ 注：i=1, 2, … N为样本采样点数；x(i)为时域信号序列。 Table 1. Characteristic parameters in time-domain
表1中，触电信号的时域特征与波形特征参数，反映了波形的集中与离散程度、能量以及波形的分布情况。特征参数包含了平均值${a_1}$、绝对平均值${a_2}$、方差${a_3}$、标准差${a_4}$、最大值${a_5}$、最小值${a_6}$、峰值${a_7}$、均方根${a_8}$、偏度${a_9}$、波形因数${a_{10}}$、能量${a_{11}}$。
除了提取时域特征数据，还通过傅里叶变换将触电电流波形变换到频域后，发现二次谐波在触电发生前一周期幅值较低，在触电发生的1个周期内幅值明显增大，故提取了二次谐波数据也作为特征数据。同时计算了10个频域特征参数。频域特征参数反映了频谱的集中与离散程度、频域振动能量以及主频带位置的变化[13]。频域特征参数的表达式如表2所示。
序号 特征表达式 序号 特征表达式 1 $ {b}_{1}=\dfrac{1}{K}\displaystyle \sum _{i=1}^{K}s\left(n\right) $ 6 $ {b}_{6}=\sqrt{\dfrac{1}{K}\displaystyle \sum _{n=1}^{K}{\left({f}_{n}-{b}_{5}\right)}^{2}s\left(n\right)} $ 2 $ {b}_{2}=\dfrac{1}{K}\displaystyle \sum _{n=1}^{K}{\left(s\left(n\right)-{b}_{1}\right)}^{2} $ 7 $ {b}_{7}=\dfrac{{b}_{6}}{{b}_{5}} $ 3 $ {b}_{3}=\dfrac{{\displaystyle \sum _n=1}^{K}{\left(s(n-{b}_{1}\right)}^{3}}{K\sqrt{{{b}_{2}}^{3}}} $ 8 $ {b}_{8}=\dfrac{\displaystyle \sum _{n=1}^{K}{\left({f}_{n}-{b}_{5}\right)}^{3}s\left(n\right)}{K{{b}_{6}}^{3}} $ 4 $ {b}_{4}=\dfrac{\displaystyle \sum _{n=1}^{K}{\left(s\left(n\right)-{b}_{1}\right)}^{4}}{K{{b}_{2}}^{2}} $ 9 $ {b}_{9}=\dfrac{\displaystyle \sum _{n=1}^{K}{\left({f}_{n}-{b}_{5}\right)}^{4}s\left(n\right)}{K{{b}_{6}}^{4}} $ 5 $ {b}_{5}=\dfrac{\displaystyle \sum _{n=1}^{K}{f}_{n}s\left(n\right)}{\displaystyle \sum _{n=1}^{K}s\left(n\right)} $ 10 $ {b}_{10}=\dfrac{\displaystyle \sum _{n=1}^{K}\sqrt{\left|{f}_{n}-{b}_{5}\right|s\left(n\right)}}{K\sqrt{{b}_{6}}} $ 注：n=1, 2, … K为谱线数；s(n)为第n条谱线的频率幅值；$ {f}_{n} $为第n条谱线的频率值。 Table 2. Characteristic parameters in frequency-domain
-
主成分分析法（PCA）是多元统计分析中比较常用的线性降维方法[14-15]。PCA通过线性投影将原始高维的数据空间映射到低维的空间中，而且使降维后的数据保留住较多的原始特征数据的特性[16]。现已被广泛应用于数据分析、机器学习等诸多领域。
上一节，从触电的剩余电流中提取了时域特征数据、频域特征数据以及二次谐波数据。这些特征数据都能够从不同方面反映出生物体的触电。但由其组成的特征向量维数较高，且部分特征数据之间又存在一定的关联性，故会存在冗余特征数据。为避免维数灾难与提高模型的识别能力，在触电故障诊断前需使用PCA将冗余特征数据去除。
首先，由于不同的特征参数包含不同性质的物理量，为消除不同特征参数之间的量纲差异，采用式（1）对数据归一化至[0, 1]区间内。
$$ f' = \frac{{f - {f_{\min }}}}{{{f_{\max }} - {f_{\min }}}} $$ (1) 式中：
$ f $ ——同一组特征数据中的某一值；
$ {f}_{{\mathrm{min}}} $ ——该组特征数据中的最小值；
$ {f}_{{\mathrm{max}}} $ ——该组特征数据中的最大值；
$ {f'} $ ——对应$ f $经归一化后的特征数据。
所有特征数据都经过标准归一化后，可用1个$ n\times p $矩阵F表示，其中n表示特征参数的个数，p表示数据样本。本次数据处理n=20，p=224。通过式（2）计算矩阵F的协方差矩阵G，协方差矩阵G为1个$ n\times n $矩阵。
$$ {\boldsymbol{G}} = \frac{{{{\boldsymbol{F}}^{\mathrm{T}}}{\boldsymbol{F}}}}{{p - 1}} $$ (2) 式中：
FT ——矩阵F的转置。
通过计算可得到协方差矩阵G的n个特征向量和n个特征值。特征向量表示协方差矩阵的主要方向，特征值表示数据沿着该方向的方差大小。将特征向量按对应特征值的大小进行排序，并选择前a个特征向量作为主成分。并将这a个特征向量按列组成1个投影矩阵M。
将矩阵F与投影矩阵M相乘，即可将原n维的特征数据集降维至a维空间之中。实现了特征维度降维，此时得到1个降维后的$ a\times p $特征矩阵。
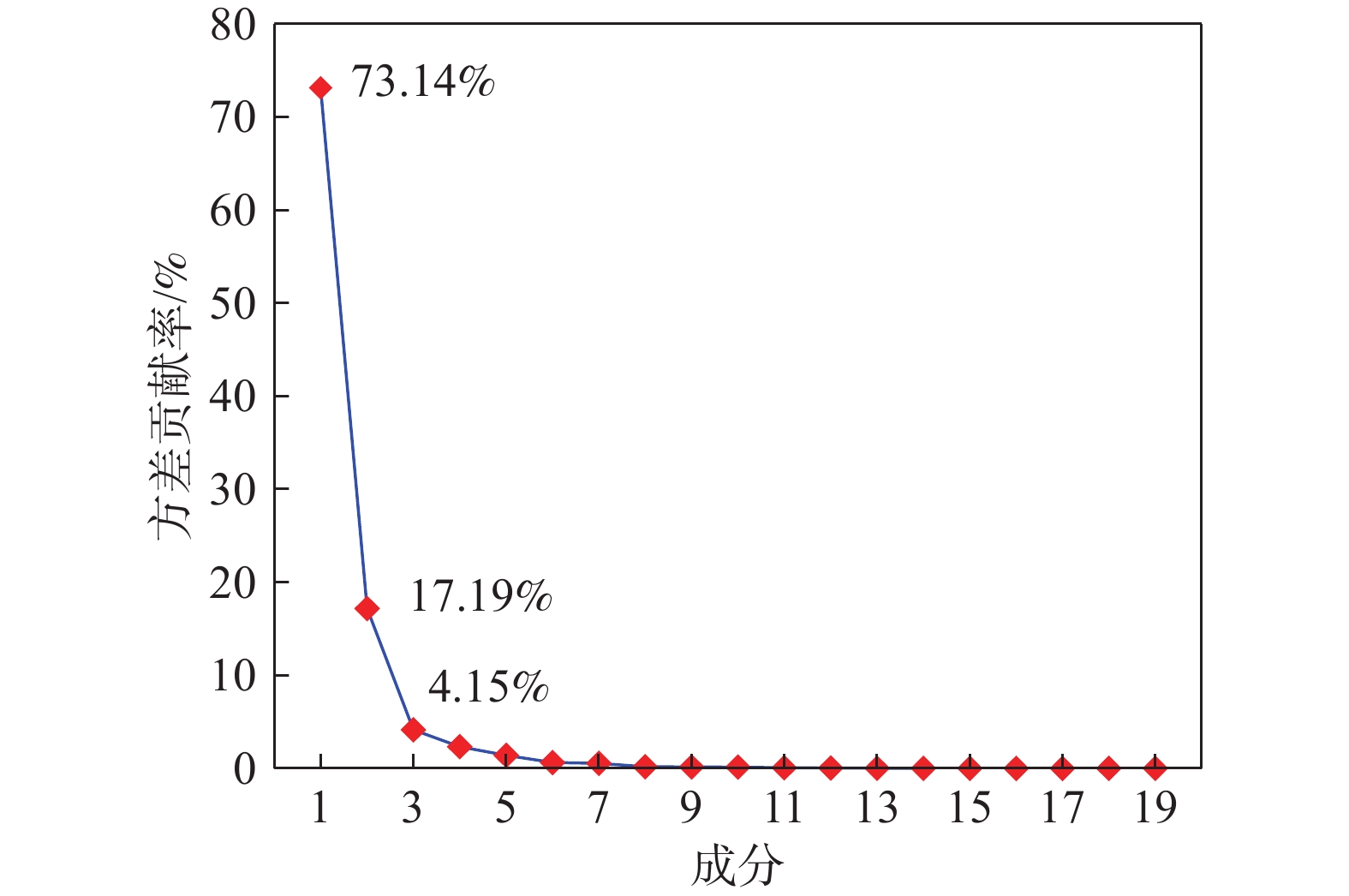
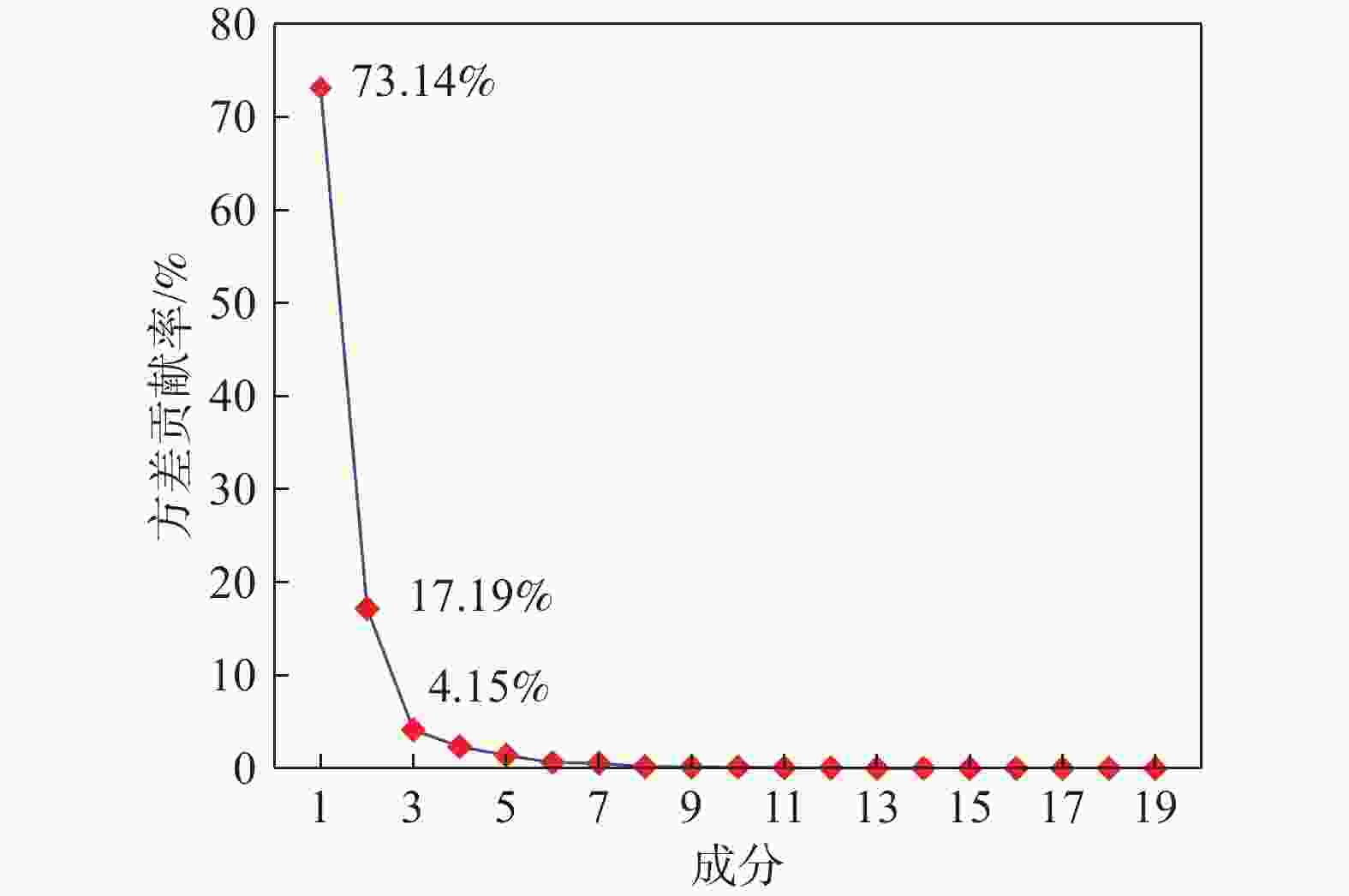
图4为方差贡献率随主成分的变化图，由图可得出，方差贡献率的变化趋势随主成分逐渐减小，并且在第3个成分之后的方差贡献率基本趋于平稳，前3个的主成分累计贡献率为94.5%。因此取前3个成分作为本次特征数据集的主成分，即可反映大部分特征数据的信息。由20个特征参数转化为3个新特征参数，达到了降维目的。
Figure 4. Changes of variance contribution rate with the variations of principal components
根据投影矩阵M，可得出3个主成分的系数，如表3所示。由表3可得出3个主成分为20个变量的线性组合。A1、A2、A3表示3个主成分，具体表达式如下：
变量 主成分1 主成分2 主成分3 $ {a}_{2} $ −0.303 66 −0.021 00 −0.064 65 $ {a}_{3} $ −0.287 23 −0.062 74 −0.006 04 $ {a}_{4} $ −0.309 25 −0.010 07 −0.097 82 $ {a}_{5} $ −0.245 79 0.042 95 −0.223 35 $ {a}_{6} $ 0.265 81 0.018 19 0.013 50 $ {a}_{7} $ −0.284 24 0.015 13 −0.136 42 $ {a}_{8} $ −0.298 28 0.013 56 −0.147 29 $ {a}_{9} $ −0.005 96 0.029 15 −0.182 84 $ {a}_{10} $ 0.149 48 0.289 35 −0.473 20 $ {a}_{11} $ −0.275 42 −0.044 56 −0.039 60 $ {b}_{1} $ −0.224 56 0.242 82 0.061 44 $ {b}_{2} $ −0.278 29 −0.063 13 −0.035 61 $ {b}_{3} $ −0.222 52 −0.279 34 0.218 72 $ {b}_{4} $ −0.246 85 −0.296 02 0.243 44 $ {b}_{6} $ −0.120 18 0.423 34 0.442 00 $ {b}_{7} $ −0.194 64 0.004 51 −0.422 94 $ {b}_{8} $ 0.053 80 −0.282 51 −0.227 29 $ {b}_{9} $ 0.024 61 −0.121 74 −0.087 29 $ {b}_{10} $ −0.178 97 0.344 54 0.259 75 $ {c}_{1} $ −0.066 40 0.534 03 −0.154 24 注：$ {c}_{1} $为二次谐波。 Table 3. Coefficients of principal components
$$ \begin{split} &{A_1} =\\& - 0.303\;66\;{a_2} - 0.287\;23\;{a_3} - 0.309\;25\;{a_4} - 0.245\;79\;{a_5}+ \\& 0.265\;81\;{a_6} - 0.284\;24\;{a_7} - 0.298\;28\;{a_8} - 0.005\;96\;{a_9} +\\& 0.149\;48\;{a_{10}} - 0.275\;42\;{a_{11}} - 0.224\;56\;{b_1} - 0.278\;29\;{b_2}- \\& 0.222\;52\;{b_3} - 0.246\;85\;{b_4} - 0.120\;18\;{b_6} - 0.194\;64\;{b_7}+ \\& 0.053\;8\;{b_8} + 0.024\;61\;{b_9} - 0.178\;97\;{b_{10}} - 0.066\;4\;{c_1} \end{split} $$ $$ \begin{split} &{A_2} =\\& - 0.021\;{a_2} - 0.062\;74\;{a_3} - 0.010\;07\;{a_4} + 0.042\;95\;{a_5}+ \\& 0.018\;19\;{a_6} + 0.015\;13\;{a_7} + 0.013\;56\;{a_8} + 0.029\;15\;{a_9}+ \\& 0.289\;35\;{a_{10}} - 0.044\;56\;{a_{11}} + 0.242\;82\;{b_1} - 0.063\;13\;{b_2}- \\& 0.279\;34\;{b_3} - 0.296\;02\;{b_4} + 0.423\;34\;{b_6} + 0.004\;51\;{b_7}- \\& 0.282\;51\;{b_8} - 0.121\;74\;{b_9} + 0.344\;54\;{b_{10}} + 0.534\;03\;{c_1} \end{split} $$ $$ \begin{split} &{A_3} =\\& - 0.064\;65\;{a_2} - 0.006\;04\;{a_3} - 0.097\;82\;{a_4} - 0.223\;35\;{a_5}+ \\& 0.013\;5\;{a_6} - 0.136\;42\;{a_7} - 0.147\;29\;{a_8} - 0.182\;84\;{a_9} -\\& 0.473\;2\;{a_{10}} - 0.039\;6\;{a_{11}} + 0.061\;44\;{b_1} - 0.035\;61\;{b_2}+ \\& 0.218\;72\;{b_3} + 0.243\;44\;{b_4} + 0.442\;{b_6} - 0.422\;94\;{b_7}- \\& 0.227\;29\;{b_8} - 0.087\;29\;{b_9} + 0.259\;75\;{b_{10}} - 0.154\;24\;{c_1} \end{split} $$ -
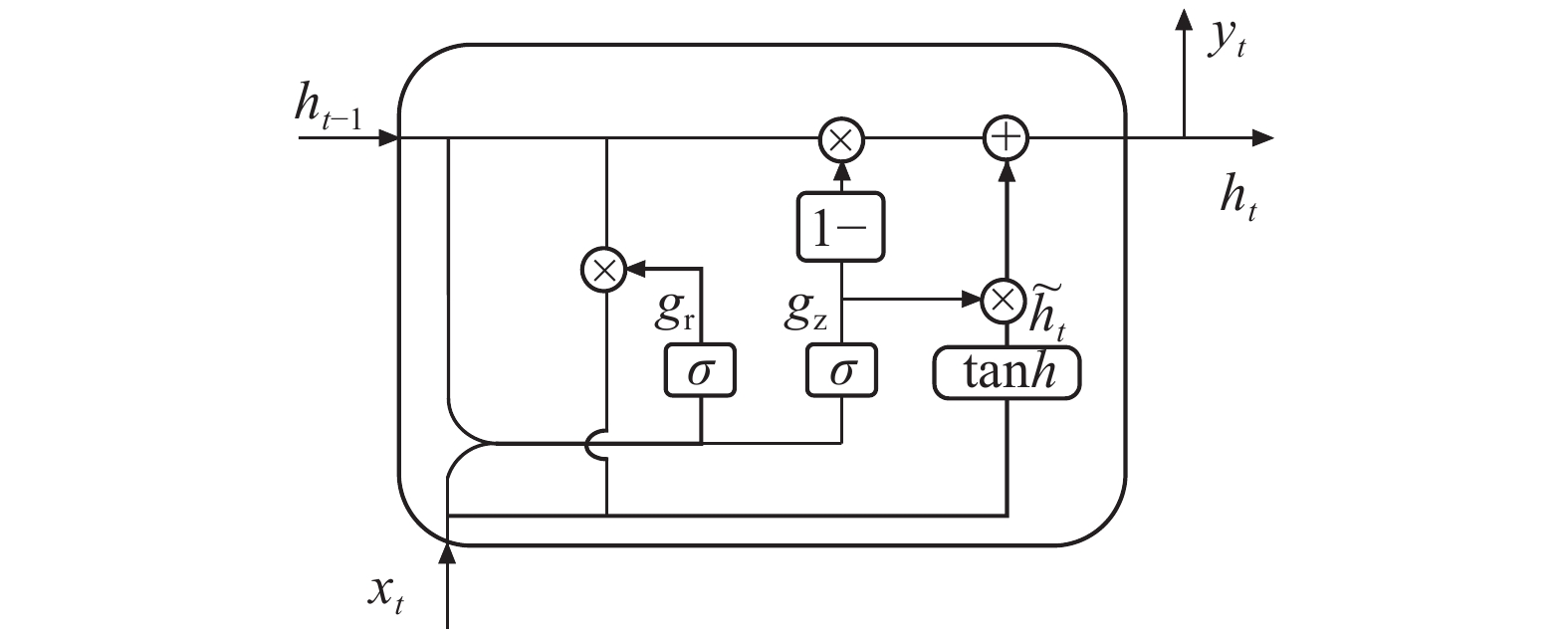
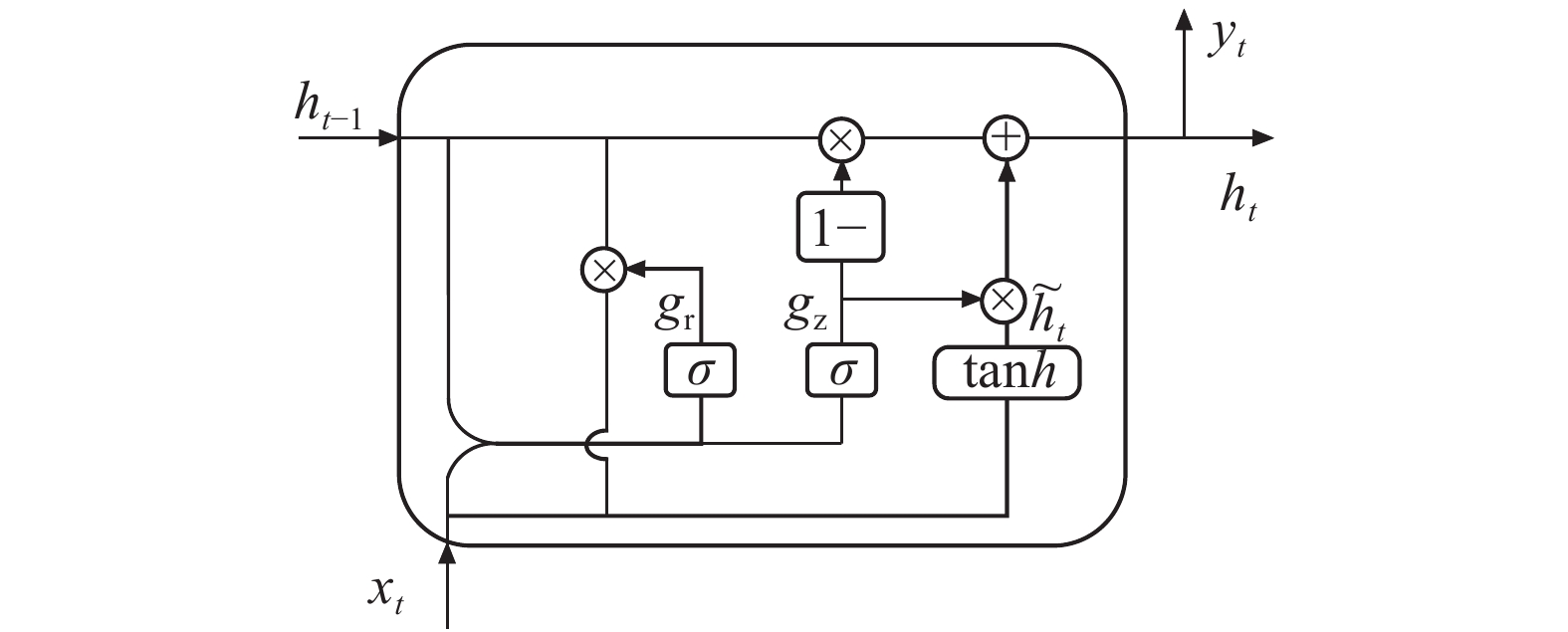
门控循环网络（Gate Recurrent Unit，GRU）是循环神经网络（Recurrent Neural Network，RNN）的1种，是长短期记忆网络（Long Short Term Memory，LSTM）的变体，它通过门结构可以有效地解决循环神经网络梯度消失和梯度爆炸的问题，并且它比LSTM网络收敛速度更快[17-18]。其细胞核结构图如图5所示。GRU模型中有两个门，重置门和更新门。GRU网络将重复的细胞核连接成链式结构，$ {x}_{t} $为输入数据，$ {y}_{t} $为输出数据。GRU网络就是通过每1个细胞核中的重置门和更新门来进行运算和数据的传播。
Figure 5. GRU cell nucleus structure diagram
重置门决定新的输入信息与历史的信息相结合，决定保留多少历史信息，重置门的值$ {g_{\mathrm{r}}} $越小，则保留上一时刻的历史信息越少[19-20]。更新公式如式（3）所示。更新门控制上一时刻的状态$ {h_{t - 1}} $和新输入$ {x_t} $对当前状态的影响程度，也就是决定了要将多少历史信息传递到未来[21-22]。更新公式如式（4）所示。
$$ {g}_{{\mathrm{r}}}=\sigma \left({W}_{r}·\left[{h}_{t-1},{x}_{t}\right]+{b}_{{\mathrm{r}}}\right) $$ (3) $$ {g}_{{\mathrm{z}}}=\sigma \left({W}_{z}·\left[{h}_{t-1},{x}_{t}\right]+{b}_{{\mathrm{z}}}\right) $$ (4) $$ {\widehat{h}}_{t}=\mathrm{tanh}\left({W}_{h}·\left[{g}_{{\mathrm{r}}}\times {h}_{t-1},{x}_{t}\right]+{b}_{{\mathrm{s}}}\right) $$ (5) $$ {h_t} = \left( {1 - {g_{\mathrm{z}}}} \right) \times {h_{t - 1}} + {g_{\mathrm{z}}} \times {\widehat h_t} $$ (6) 式中：
$ {g_{\mathrm{r}}} $、$ {g_{\mathrm{z}}} $、$ {\widehat h_t} $、$ {h_t} $——重置门、更新门、候选隐藏状态及当前隐藏状态；
$ W $ ——权重；
$ b $ ——偏置；
$ \sigma (·) $ ——sigmoid函数，使用此函数可以将数据限制在[0, 1]范围内[23]，如式（7）所示；
$ {\mathrm{tan}}h(·) $ ——tanh函数，使用此函数可以将数据限制在[−1, 1]范围内，如式（8）所示。
$$ \sigma \left( x \right) = \frac{1}{{1 + {{\mathrm{e}}^{ - x}}}} $$ (7) $$ \tan h \left( x \right) = \frac{{{{\mathrm{e}}^{2x}} - 1}}{{{{\mathrm{e}}^{2x}} + 1}} $$ (8) -
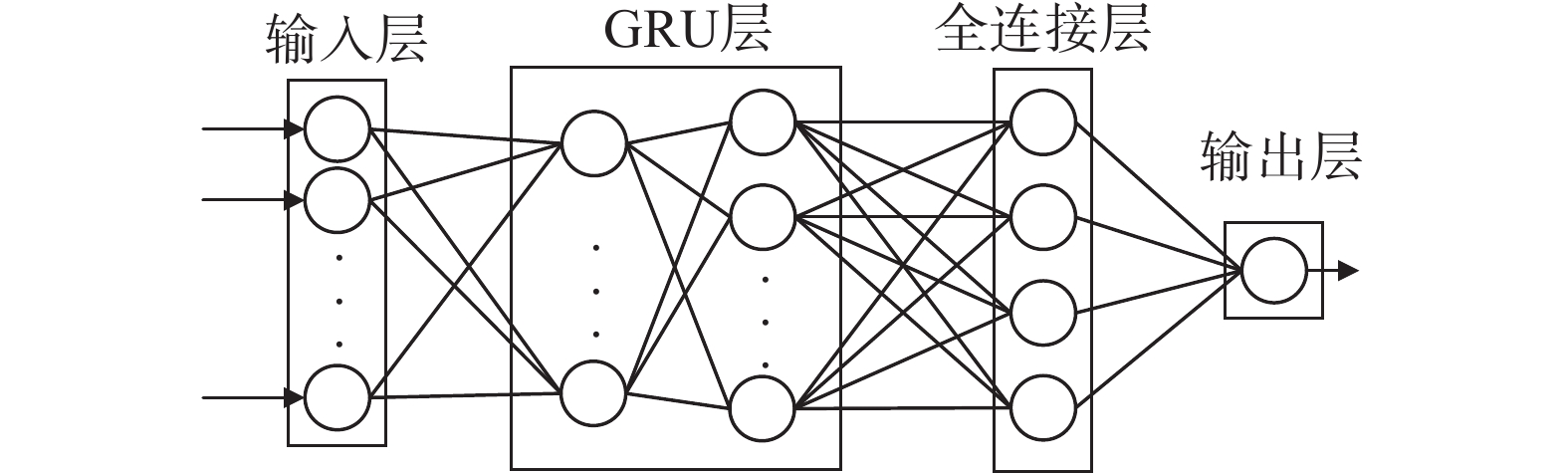
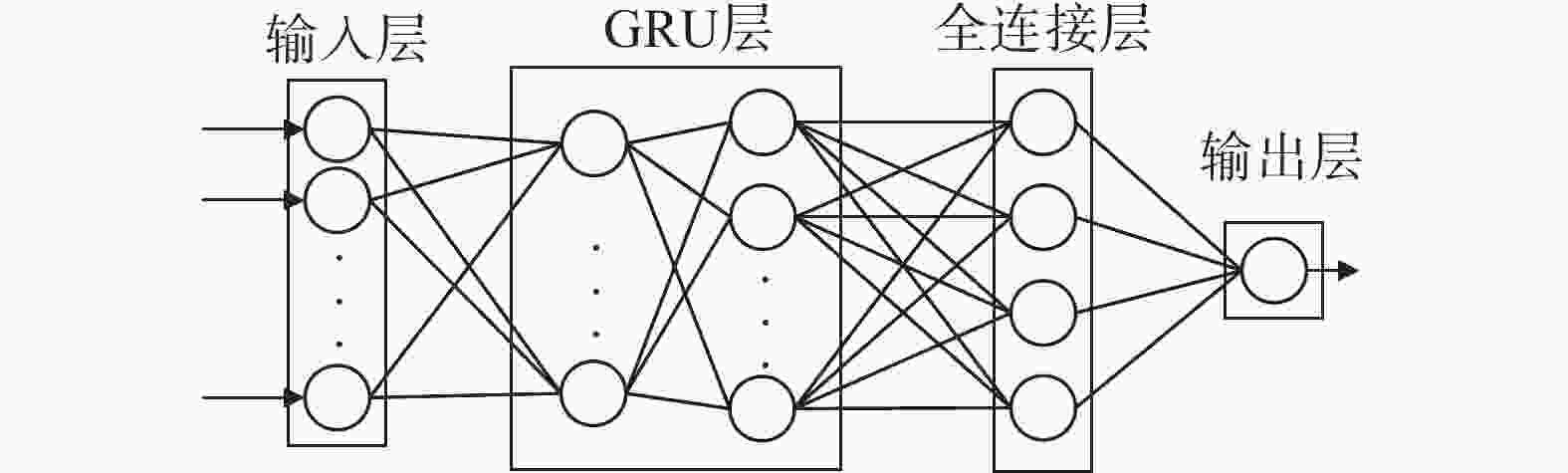
GRU神经网络模型由输入层、GRU网络层、全连接层和输出层构成[24]，如图6所示。
Figure 6. GRU neural network structure diagram
为了能获得性能较好的模型，需要对GRU网络层数和神经元数进行参数调优。理论上，增加网络层数能增强拟合能力，提升效果。但是实际上，过多的网络层数会导致过拟合和训练难度加大，使模型难以收敛。因此，设置迭代次数为30的实验测试，固定神经元个数为64，改变不同的网络层数，通过式（9）计算对应网络层数的平均绝对误差值（MAE），实验结果如表4所示。
当前GRU网络层数 神经元个数/个 MAE 1 64 0.200 0 2 64 0.133 3 3 64 0.233 3 4 64 0.200 0 Table 4. Number of GRU network layers and MAE
$$ {\mathrm{MAE}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left|\; {{{\widehat y}_i} - {y_i}}\; \right|} $$ (9) 式中：
$ {\widehat y_i} $ ——预测值；
$ {y_i} $ ——实际值。
误差越小，MAE值也越小，说明该网络层数对应的模型具有更高的精确度。通过表4可知，GRU网络层数为2时，MAE值最小，因此确定GRU网络层数为2。
同理，神经元个数不同也会对模型的性能造成影响。在GRU层中神经元个数少会造成欠拟合，而神经元个数过多会造成过拟合问题。因此，选择1个合适的神经数量是比较重要的。设置迭代次数为30的实验测试，固定GRU网络层数为2，改变不同的神经元个数，通过式（9）计算对应神经元数的平均绝对误差值，实验结果如表5所示。
当前GRU网络层数 神经元个数/个 MAE 2 8 0.433 3 2 16 0.400 0 2 32 0.266 6 2 64 0.200 0 2 128 0.300 0 Table 5. Number of neurons and MAE
通过表5可知，神经元数为64时，MAE值最小，因此确定神经元数为64。
学习率用于确定每次迭代的步长，属于优化算法的调谐参数。设置合适的学习率，可使损失函数收敛到最小值，也就是使预测值与真实值的差距达到最小。损失值越小，说明模型的预测效果越好。设置不同学习率的实验测试，可得到不同的损失值，实验结果如表6所示。
学习率 0.000 8 0.000 9 0.001 0 0.002 0 0.003 0 损失值 0.265 5 0.241 2 0.240 3 0.273 9 0.248 3 Table 6. Learning rate and loss value
通过表6可知，当学习率为0.001 0时，损失值最小，因此取学习率为0.001 0。
因此，GRU神经网络结构图中输入层为3个主成分的数据特征参数；两层GRU网络层中各有64个神经元；全连接层有4类，分别表示：三相平衡正常、三相平衡触电、三相不平衡正常以及三相不平衡触电；输出层为输出4类触电中的1种。训练迭代次数为300，学习率取0.001 0。
-
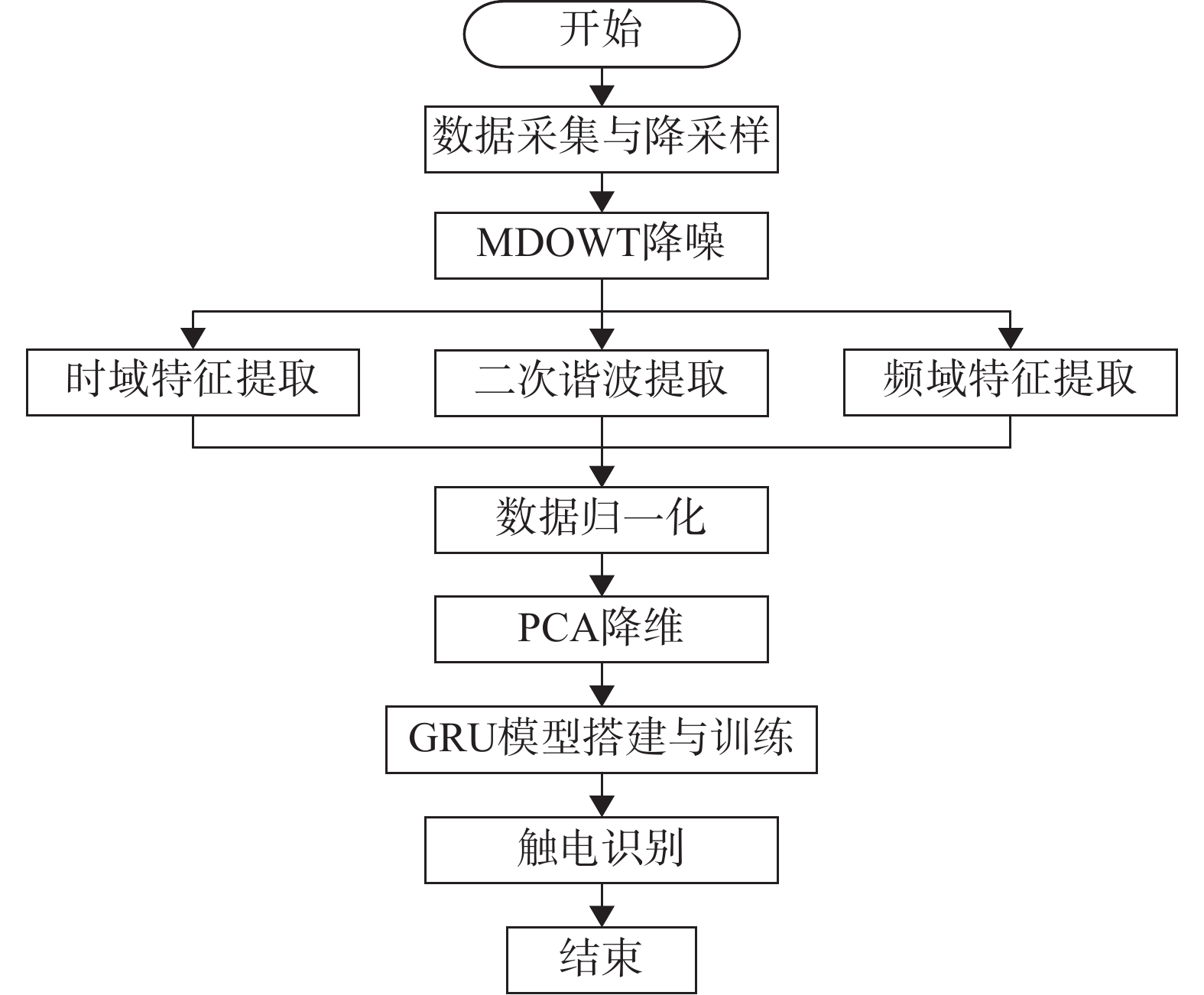
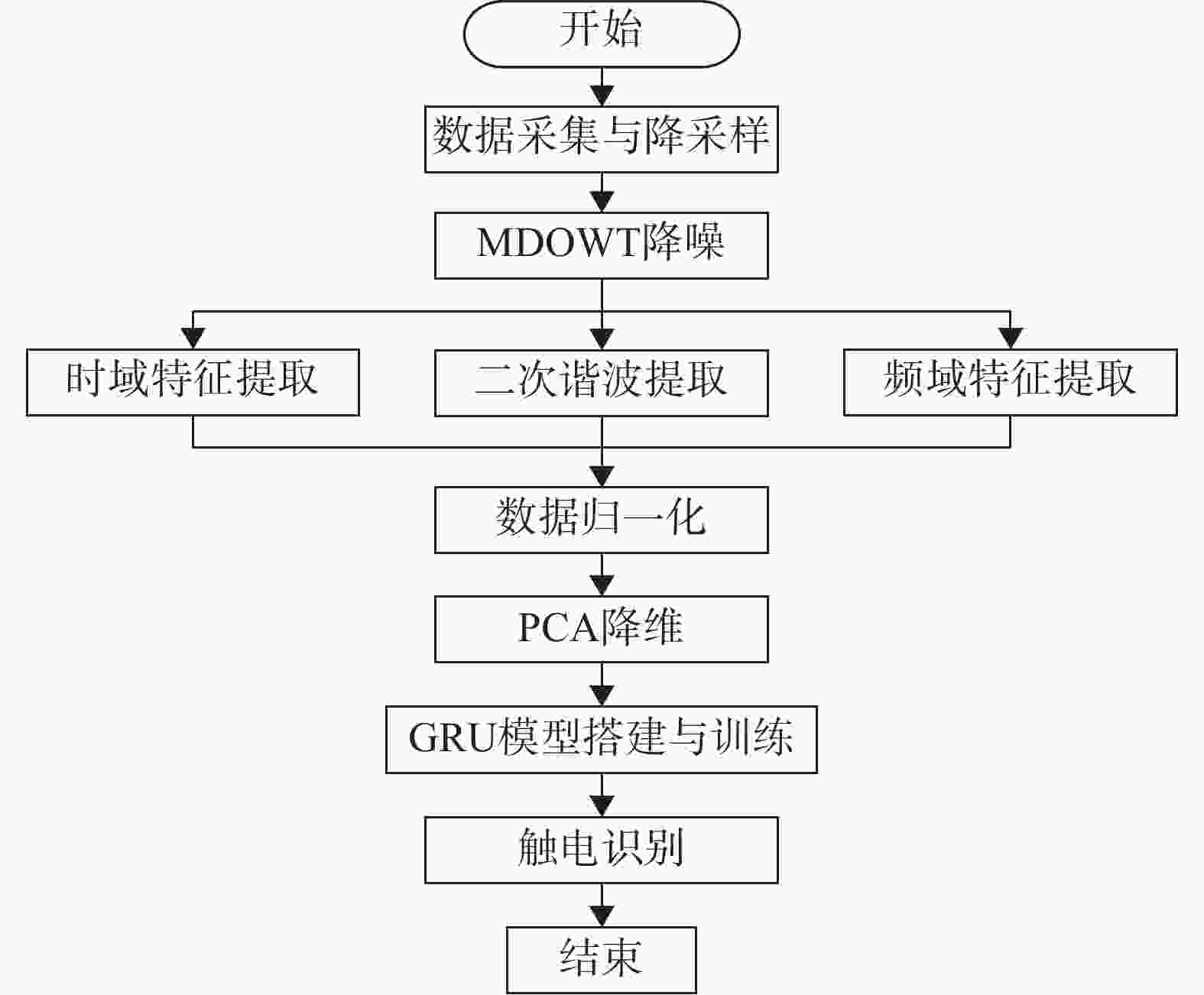
本次实验采集的224组样本数据中，三相平衡触电信号、三相平衡正常信号、三相不平衡触电信号以及三相不平衡正常信号4类样本数据各56组。再取四类样本数据各35组，共140组作为训练集；取四类样本数据各15组，共60组作为测试集；剩下的24组样本数据作为验证集。触电诊断流程图如图7所示。第一步，通过以猪肉作为触电体的触电实验，获取触电剩余电流信号；第二步，对获取的数据降采样处理后，使用最大重叠离散小波变换进行降噪处理；第三步，对降噪后的剩余电流信号进行时域和频域分析，提取时域和频域特征数据，同时提取触电波形的二次谐波幅值特征数据；第四步，对提取的特征数据进行归一化处理后，再进行PCA降维得到3个新的特征数据；第五步，搭建GRU触电诊断模型，并且把3个新的特征数据集划分为训练集、测试集以及验证集作为模型输入，进行训练与验证；最后，运用训练得到的模型，输入任意1组数据，进行触电诊断。
Figure 7. Electrocution diagnosis flow chart
-
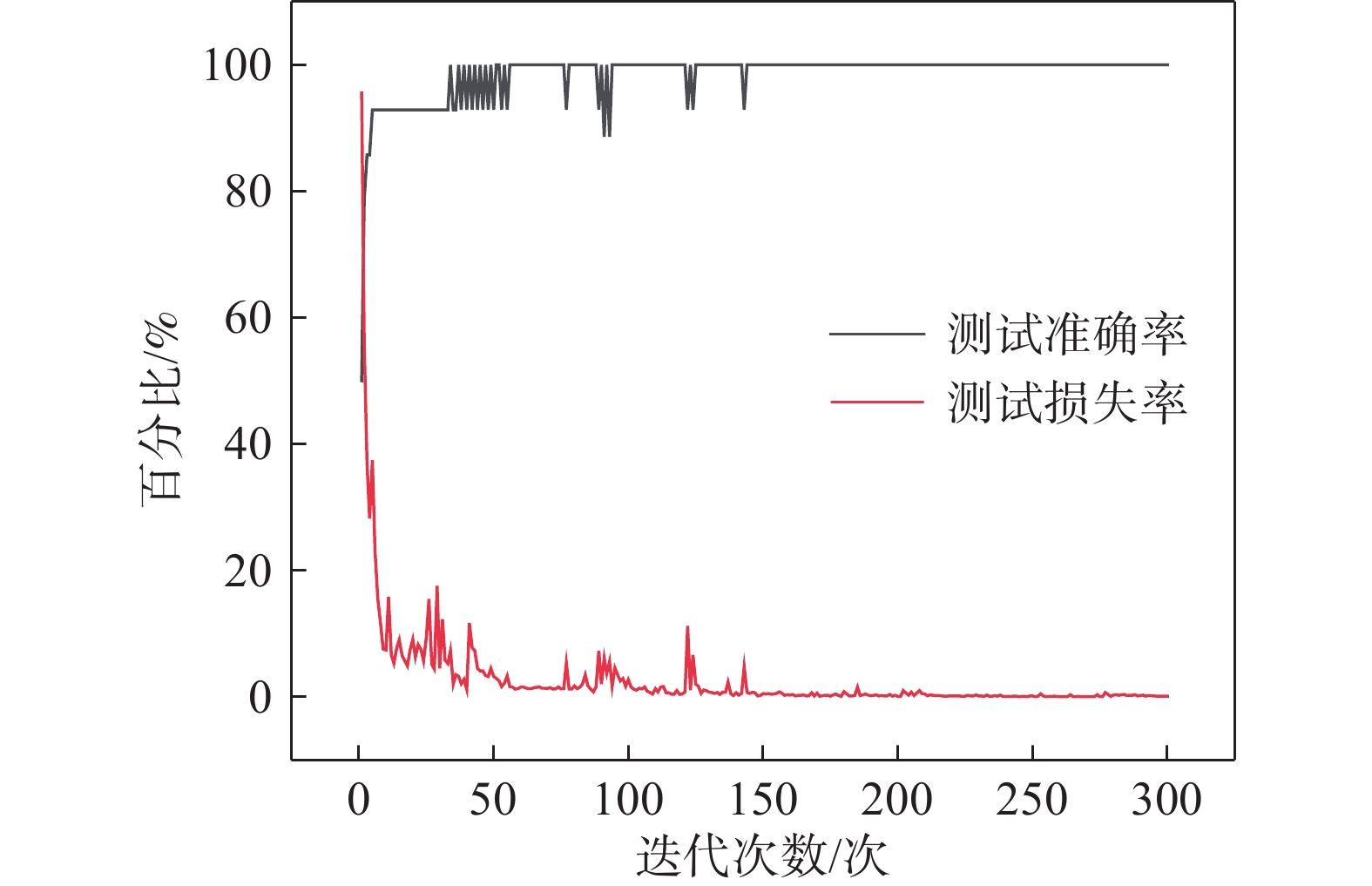
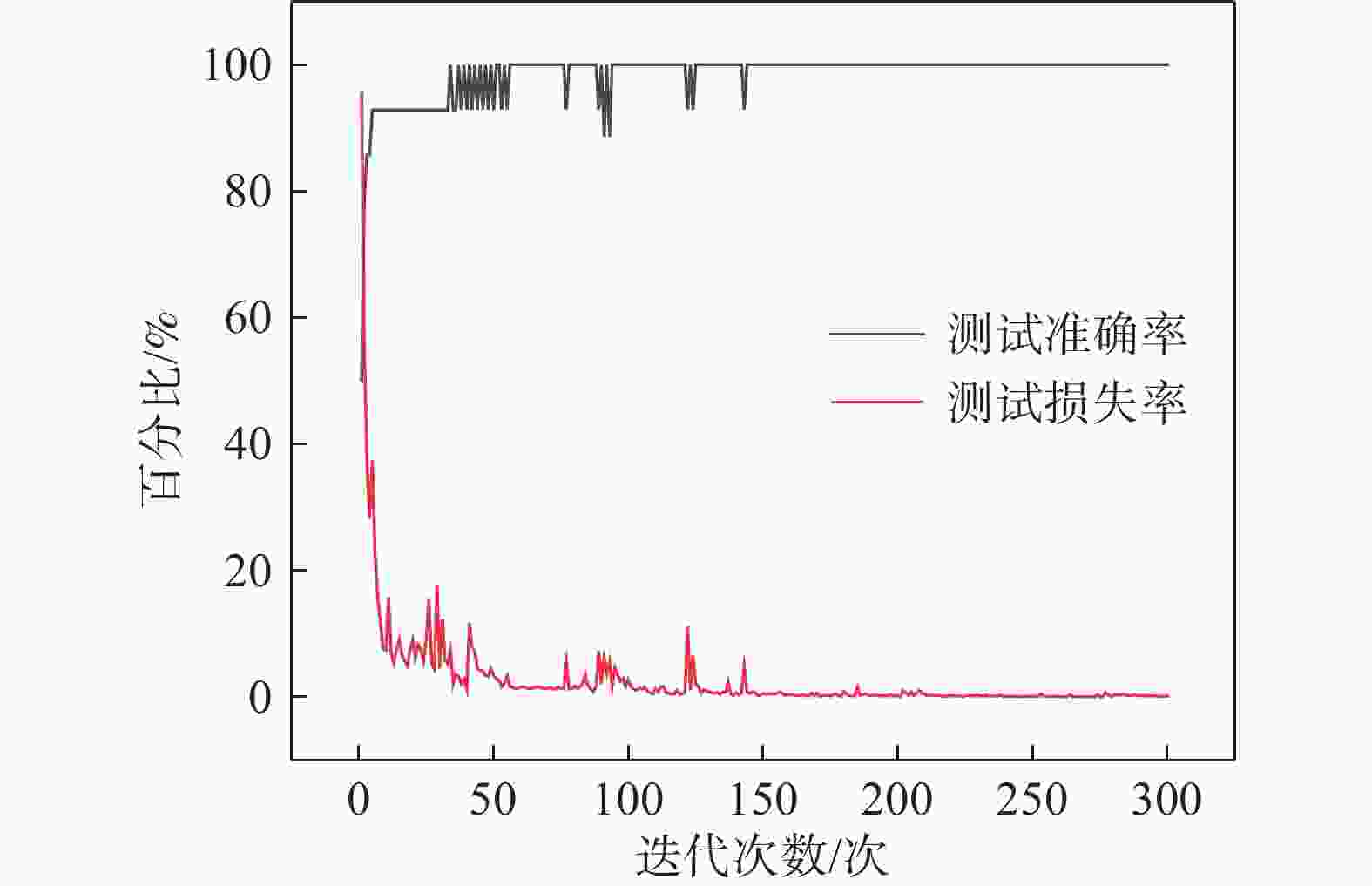
在训练过程中，随着GRU模型迭代次数的增加，测试的损失函数率不断减少直至收敛。同时，测试准确率不断提升向100%趋近，说明了该模型能较好地学习输入的特征数据。虽然在训练过程中，损失值出现过几次突增，随后极速下降，但是总体呈现下降并且不断向0趋近。在损失值发生较大的震荡时，准确率也伴随着震荡，产生这一现象可能是参数训练过程中，模型陷入了局部最优。随着迭代次数的增加，训练参数得到不断更新到最佳，最后两条曲线趋于稳定，实验结果如图8所示。
Figure 8. Schematic diagram of the testing process
-
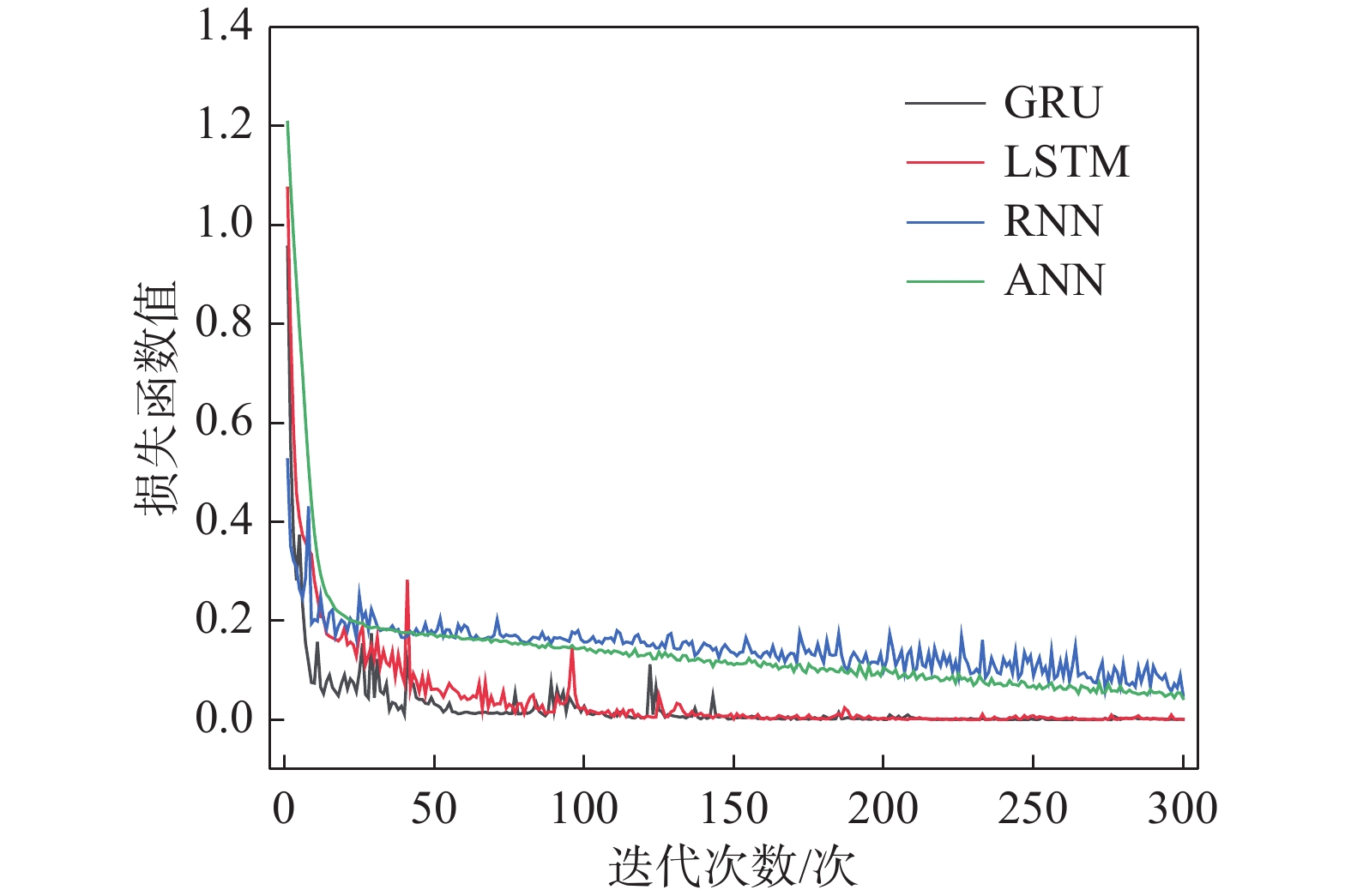
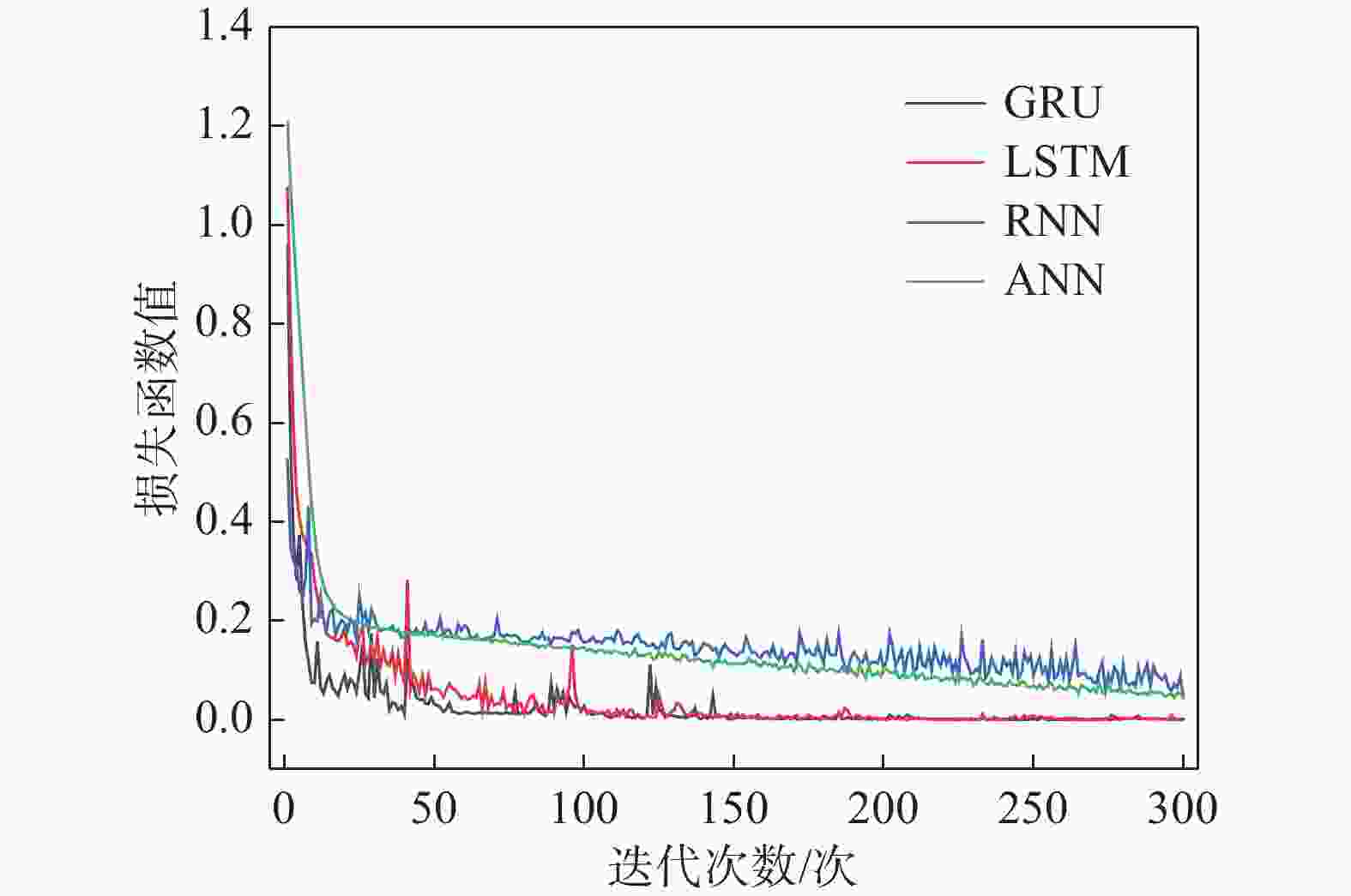
本次实验使用长短期记忆网络LSTM、循环神经网络RNN、人工神经网络ANN（Artificial Neural Network）以及支持向量机SVM（Support Vector Machine）4种模型来做比较。SVM属于机器学习，其余模型都属于深度学习。图9显示了深度学习的4个模型的损失函数值随着迭代次数增加而变化的情况。结果表明，4个模型的损失函数值均随着迭代次数的增加而逐渐减小，其中GRU收敛效果最好，LSTM次之。RNN的收敛结果有明显的波动，同时RNN与ANN的收敛值都较大。因此，GRU模型具有训练效果。
Figure 9. Relationship between the number of iterations and the loss function
表7显示了5种模型在迭代次数为300时的触电识别准确率以及训练时间。结果表明，GRU与LSTM具有较高的准确率98.33%，RNN、ANN与SVM的准确率较低，仅91.67%。同时，在相同的准确率下，GRU的训练时间较LSTM短，这是因为GRU网络较LSTM网络更简单。
神经网络 迭代次数/次 准确率/% 训练时间/s GRU 300 98.33 6.559 0 LSTM 300 98.33 6.883 7 RNN 300 91.67 4.551 8 ANN 300 91.67 11.675 4 SVM 300 91.67 0.001 0 Table 7. Performance comparison of different models
-
1）在三相平衡与三相不平衡的触电实验上，本文对生物体触电剩余电流信号进行采集，再对电流信号进行降采样和降噪处理，提取出时频域统计参数和二次谐波幅值参数。各参数均能从不同方面表征生物体触电信号的特征。
2）运用主成分分析法将原始提取的20个特征量降为3个新的特征量，并将新的三维特征量参数作为触电诊断模型的输入向量，进行触电故障类型诊断，大大提高了诊断的准确率。
3）通过GRU、LSTM、RNN、ANN和SVM 5种网络分别对降维后新的特征参数进行触电类型诊断，对比实验结果得出，GRU模型对触电信号故障类型诊断具有更好的效果。
Analysis on Electrocution Diagnosis Based on Discrete Wavelet Transform and GRU
doi: 10.16516/j.ceec.2024.4.13
- Received Date: 2023-04-29
- Rev Recd Date: 2023-08-03
- Available Online: 2024-07-12
- Publish Date: 2024-07-30
-
Key words:
- low-voltage distribution network /
- electrocution diagnosis /
- wavelet denoising /
- feature extraction /
- principal component analysis /
- GRU
Abstract:
| Citation: | CAI Gaofeng, WANG Qingbin, CHEN Zhenyu, et al. Analysis on electrocution diagnosis based on discrete wavelet transform and GRU [J]. Southern energy construction, 2024, 11(4): 127-136 doi: 10.16516/j.ceec.2024.4.13
|
DownLoad:
