-
采用预应力锚栓式连接的风力发电机组的基础（以下简称“风机基础”），通过在预应力锚栓施加预应力，来产生足够的压应力抵抗风力发电机组传递给基础的弯矩而产生的拉应力。这种传力形式，形成了一种圆环形均布荷载的力学特点。针对这种形式，目前主流的设计规范[1-3]未给出相应的设计方法。由于风电行业的快速发展，许多学者开展了对风机基础的研究 ，包括根据《混凝土结构设计规范》中的局压设计公式，给出了风机基础锚板下混凝土的配筋设计方法、利用有限元分析法对风机基础进行了力学特征分析，揭示了风机基础的力学分布特点、利用有限元分析法证明基础锚栓锚板压的受力特征符合局压受力特征等结论[4-16]。但都未对基础应力提出一种解析解或近似解。
根据目前研究成果[17-19]，研究学者对圆形或矩形范围内中心点以下的竖向附加应力解析解进行了推导论证。而对于风机基础这种圆环形受力范围内，圆环宽度中线以下的附加应力解析解研究较少。为此文章给出一个求解思路，并通过有限元分析软件进行验证，论证了该思路的可靠性。为风机基础核心区设计提供了一条思路。
-
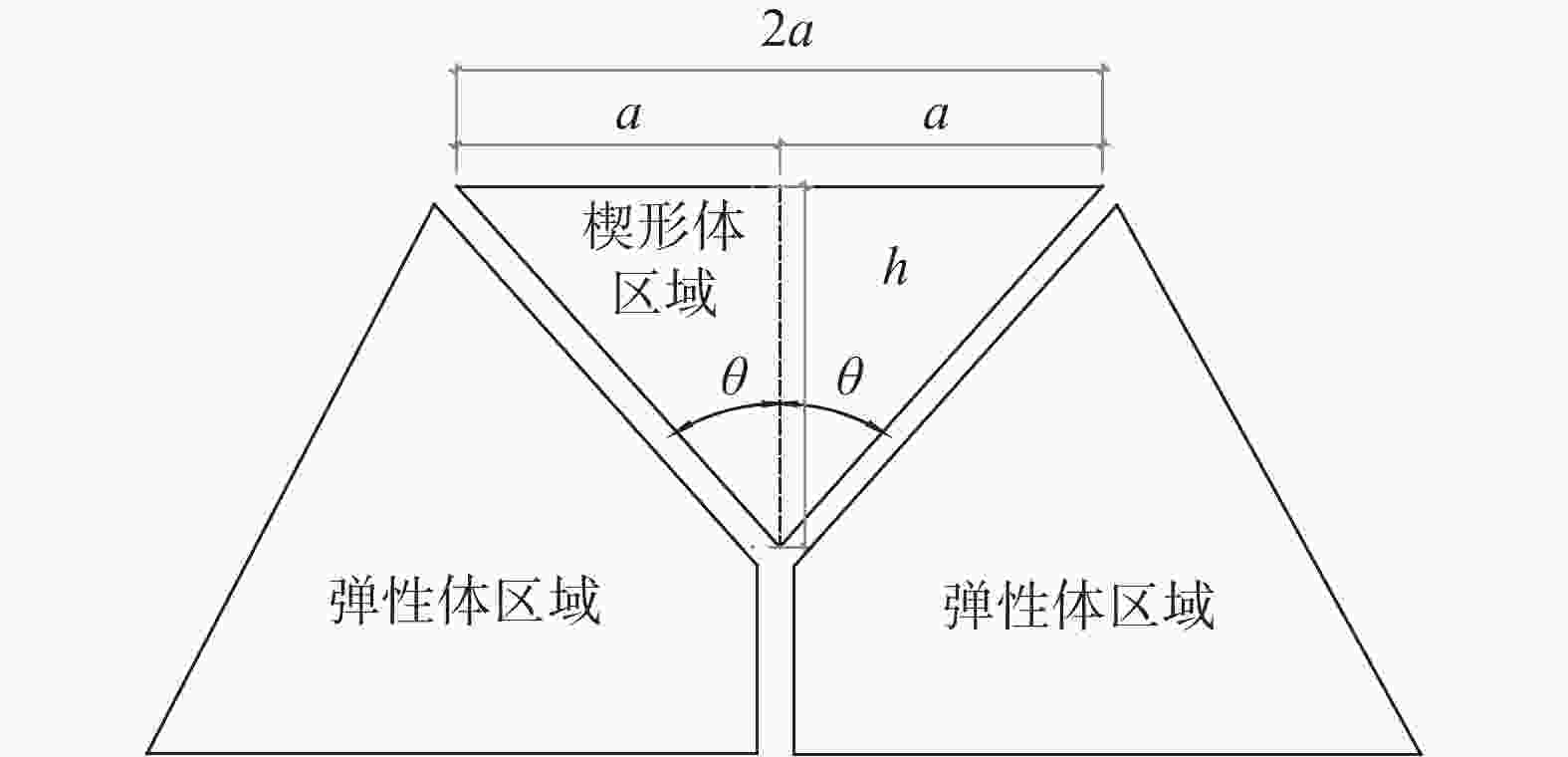
混凝土局压理论[20-22]认为,混凝土在承受局部受压荷载的过程中，随着外荷载的增加，核心受压混凝土逐步形成由剪切破坏形成的楔形体，进一步的产生了劈裂力，导致构件的破坏。在楔形体区域以外的弹性体区域，主要受力形式为压应力及压应力产生劈裂力。
基于上述理论，基础在锚栓锚板的作用下，可以认为是局压破坏形式，受力机理如图1所示。
Figure 1. Calculation model of local compressive strength of concrete
-
在临近破坏阶段，楔形体的破坏机理为剪切破坏，适用摩尔库伦强度准则。有:
$$ \frac{{{\sigma _1} - {\sigma _3}}}{2} = c\cos \varphi + \frac{{({\sigma _1} + {\sigma _3})\sin \varphi }}{2} $$ (1) 式中：
$ {\sigma _1} $——基础混凝土第一主应力（MPa）；
$ {\sigma _3} $——基础混凝土第三主应力（MPa）；
$ c $ ——混凝土粘聚力（MPa）；
$\varphi $ ——混凝土内摩擦角 （°）。
令$u = \tan \varphi $ 代入（1）得：
$$ {(u + \sqrt {1 + {u^2}} )^2}{\sigma _1} - {\sigma _3} = 2c\left( {u + \sqrt {1 + {u^2}} } \right) $$ (2) 令m=$u + \sqrt {1 + {u^2}} $代入（2）得：
$$ {m^2}{\sigma _1} - {\sigma _3} = {2cm} $$ (3) 考虑混凝土材料为单向受拉状态时：${\sigma _3} = 0$
上式为：
$$ {m^2}{\sigma _1} = {m^2}{f_t} = {2cm} $$ (4) 考虑混凝土材料为单向受压状态时：${\sigma _1} = 0$
上式为：
$$ {\sigma _3} = {f_c} = {2cm} $$ (5) 基础设计往往采用C40混凝土，其抗拉强度设计值为${f_t} = 1.71{\text{(N/m}}{{\text{m}}^{\text{2}}}{\text{)}}$及抗压强度设计值为$ {f_c} = 19.1{\text{(N/m}}{{\text{m}}^{\text{2}}}{\text{)}} $，将公式（4）/（5）有
$$ {m^2} = \frac{{{f_c}}}{{{f_t}}} = \frac{{19.1}}{{1.71}} = 11.169\;6 $$ (6) 求解得$\varphi = $56.683°
按照摩尔强度理论有，剪切破坏面与第一主应力${\sigma _1}$ 的夹角为：
$$ \theta = 45^\circ - \frac{\varphi }{2} = 16.658\;5^\circ $$ (7) 则有楔形体高度：
$$ {h} = \frac{{a}}{{\cos \theta }} $$ (8) 式中：
$2a$ ——承受局部荷载的受力长度（m）；
$2\theta $ ——楔形体的破坏角（°）。
在楔形体高度范围内的配筋计算可以按照《混凝土结构设计规范》第6.6.3条进行设计。
-
基础局压楔形体以外的区间应力水平明显低于楔形体区域。在楔形体剪切破坏前都属于弹性变形阶段，可以认为是小变形的问题，在不考虑钢筋的加强作用前提下，基础混凝土结构满足连续均匀连续体的弹性力学基本假定。故可以采用弹性力学理论求解该区域的应力水平。
基于弹性力学的理论分析，在半空间弹性体表面作用竖向集中力F时，弹性体内部的任一点的应力有Boussinsq解答[23]，如下所示。
$$ {\sigma _{\text{z}}} = \frac{{3F{z^3}}}{{2\text{π} {R^5}}} $$ (9) 式中：
${\sigma _{\text{z}}}$——任意一点竖向应力（MPa）；
$F$ ——分析单元所受外荷载，对于微分单元为均布荷载大小值（kN）；
$z$ ——所求点距离载荷作用面的垂直距离(m);
$R$ ——为所求点距离集中力F的空间距离(m)。
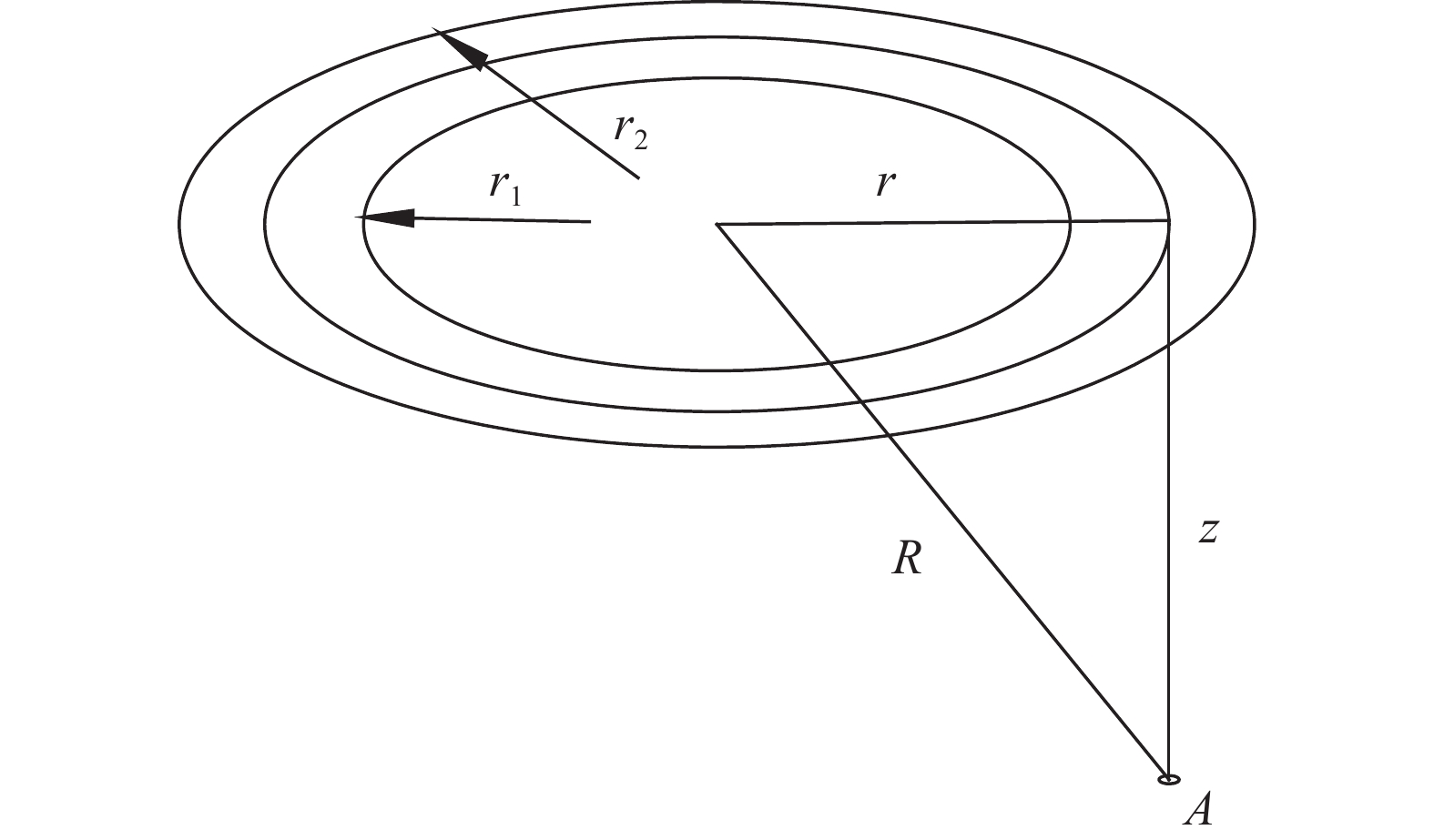
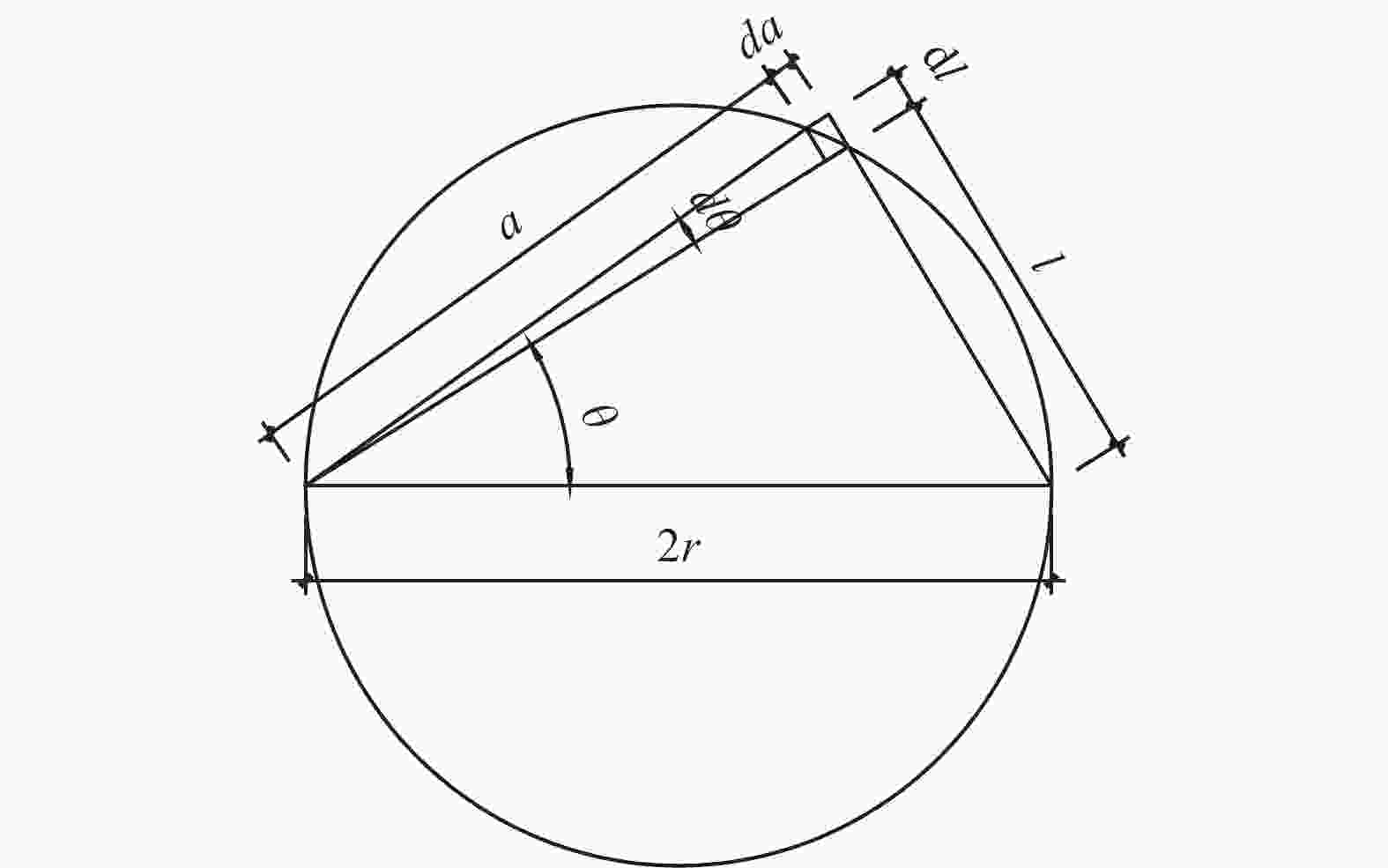
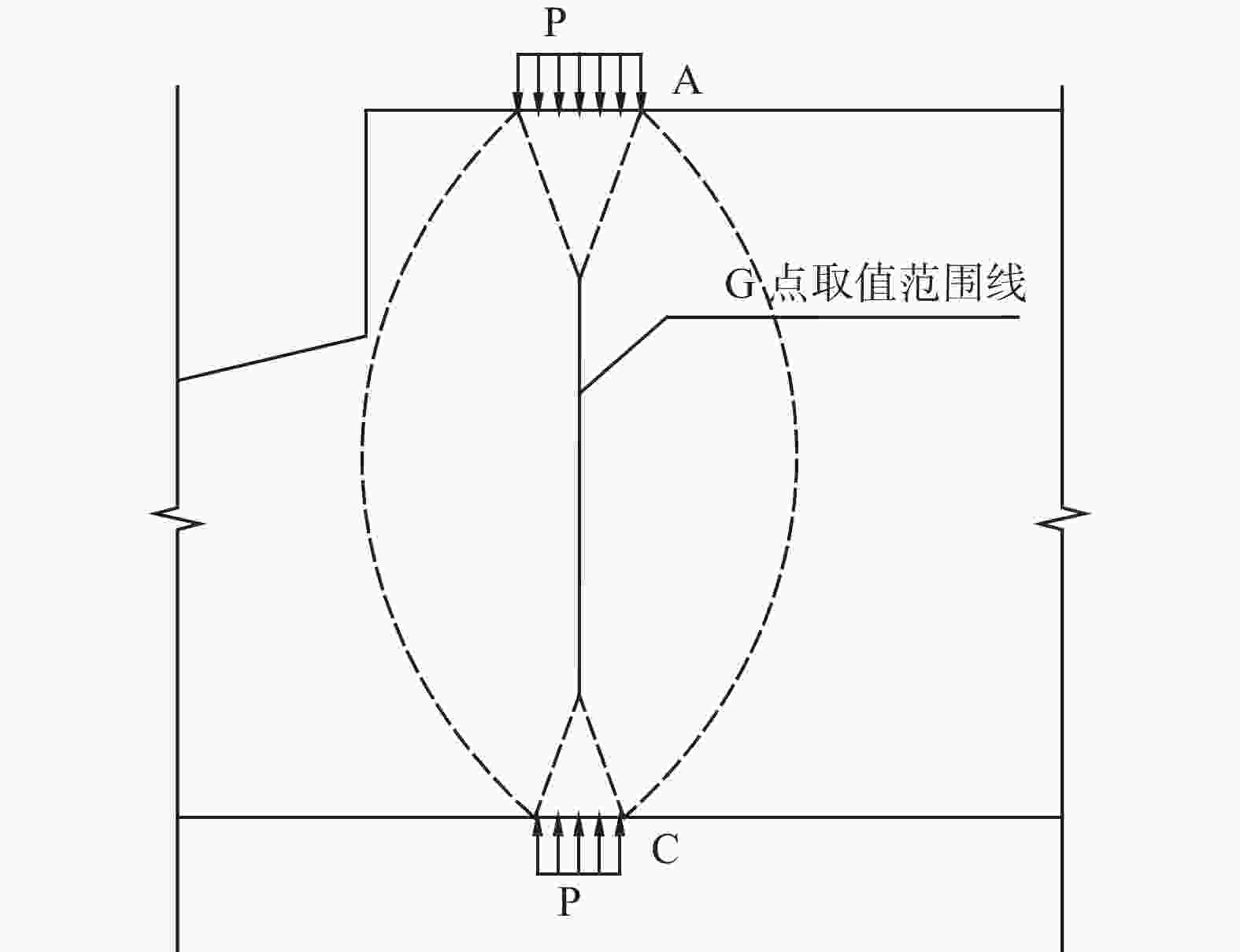
对于风机基础这种圆环形受力范围内，圆环宽度中线以下的附加应力解析解，本文给出一个求解思路如图2和图3所示。
Figure 2. Derivation 1 of vertical additional stress under circular loading
Figure 3. Derivation 2 of vertical additional stress under circular loading
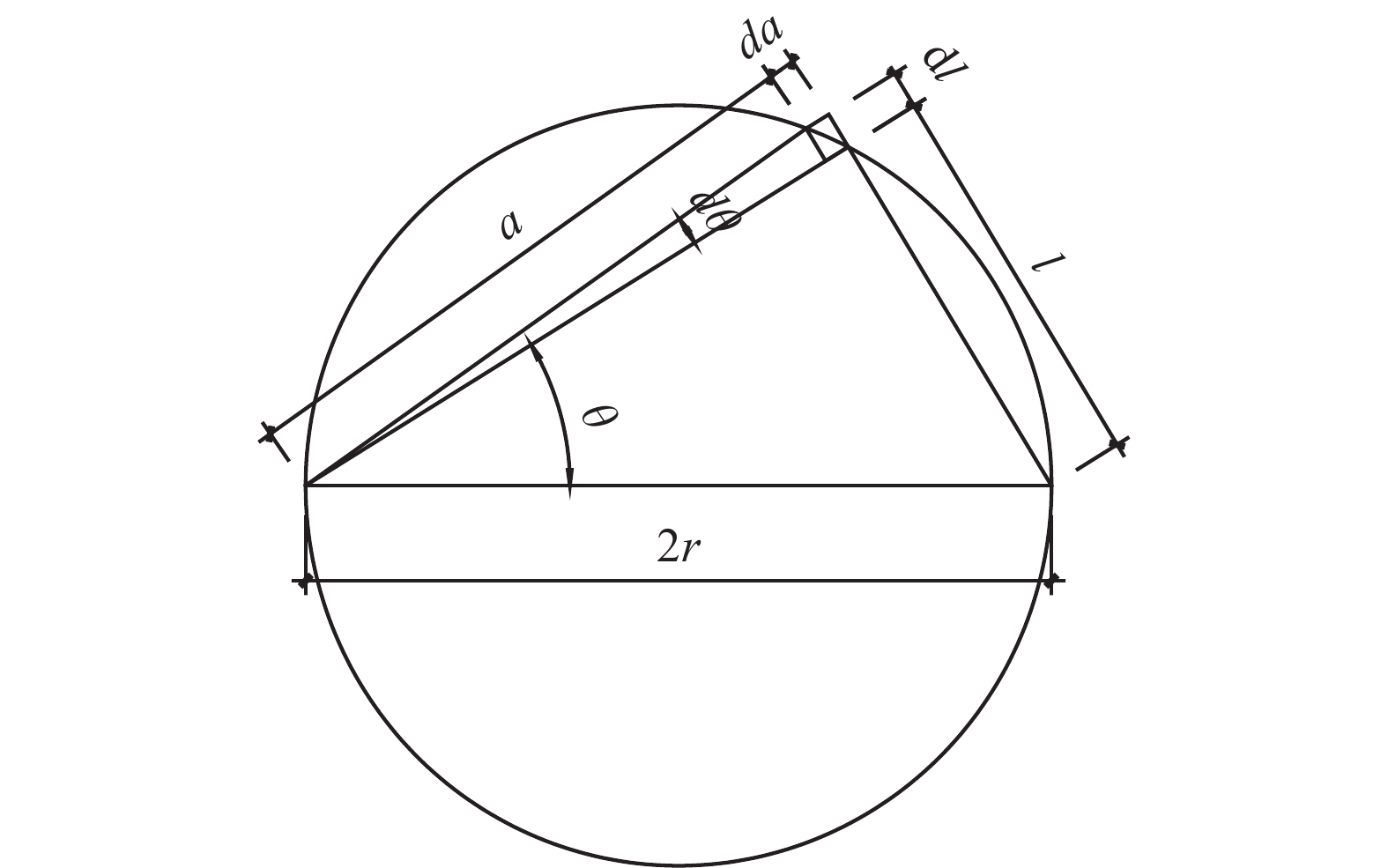
$$ {R^2} = {r^2} + {z^2} $$ (10) $$ a = 2r \times \cos\theta $$ (11) $$ l = 2r \times \sin \theta $$ (12) $$ {\mathrm{d}}l = a \times {\mathrm{d}}\theta $$ (13) 式中：
$ A $ ——所求应力状态点；
$ r $ ——A点所在分度圆距离圆环荷载圆心距离（m）；
$ l $ ——圆环上荷载点距离A点的水平距离（m）；
$ a $ ——局部施加的均布荷载的作用长度（m）；
$ \theta $ ——计算变量；
$ {\mathrm{d}}l、{\mathrm{d}}a $ ——荷载微分点的长宽（m）；
$ {r_1} $ ——圆环形荷载内直径（m）；
$ {r_2} $ ——圆环形荷载外直径（m）；
对于圆环均布荷载作用下，任一点A的竖向应力有：
$$ {\sigma _z} = \iint\limits_D {{\mathrm{d}}{\sigma _z}} $$ (14) D ——圆环形荷载面积（m2）。
根据积分面积的对称性及将公式（9）~公式（13）带入公式（14）有：
$$ {\sigma _z} = 2\int_{r1}^{r2} {\int_0^{\tfrac{\text{π} }{2}} {\frac{{3F{z^3} \times 2 \times r \times \cos \theta }}{{2\text{π} {{(4 \times {r^2} \times {{\sin }^2}\theta + {z^2})}^{\frac{5}{2}}}}}} } {\mathrm{d}}\theta {\mathrm{d}}a $$ (15) 由于$ a $的长度难以通过变量$ \theta $表示，故为了化简上式，根据简单的力学原理，并令$ {m} = \dfrac{z}{{2r}} $有：
$$ \begin{gathered} {\sigma _z} = 2\int_{r1}^{r2} {\int_0^{\tfrac{\text{π}}{2}} {\frac{{3F{z^3} \times 2 \times r \times \cos \theta }}{{2\text{π} {{(4 \times {r^2} \times {{\sin }^2}\theta + {z^2})}^{\frac{5}{2}}}}}} } {\mathrm{d}}\theta {\mathrm{d}}a\leqslant \\ 2 \times b \times \frac{{3F{z^3}}}{{2\text{π} \times {{(2r)}^4}}} \times \int_0^{\frac{\text{π}}{2}} {\frac{{\cos \theta }}{{{{({{\sin }^2}\theta + {m^2})}^{\frac{5}{2}}}}}} {\mathrm{d}}\theta \\ \end{gathered} $$ (16) 式中：
$ b $ ——圆环形荷载的宽度（m），$ b = {r_1} - {r_2} $
通过观察式（16），我们可令
$$ {\sigma _z} = 2 \times b \times \frac{{3F{z^3}}}{{2\text{π} \times {{(2r)}^4}}} \times {{{K}}_\alpha } $$ (17) 式中：
$ {{{K}}_\alpha } $——即为圆环形荷载的基底附加应力系数。
$ {{{K}}_\alpha } $可通过数值分析软件编程求解，如Matlab、Mathematica等，由于$ {{{K}}_\alpha } $仅与m值有关，通过对m值进行赋值并制成表1，实现对基础核心区竖向应力的快捷计算。
m $ {{{K}}_\alpha } $ m $ {{{K}}_\alpha } $ m $ {{{K}}_\alpha } $ m $ {{{K}}_\alpha } $ 0.10 6666.42 0.30 82.09 0.50 10.49 0.70 2.65 0.12 3214.78 0.32 63.37 0.52 8.95 0.72 2.36 0.14 1735.15 0.34 49.68 0.54 7.68 0.74 2.10 0.16 1017.01 0.36 39.49 0.56 6.62 0.76 1.88 0.18 634.83 0.38 31.77 0.58 5.74 0.78 1.69 0.20 416.43 0.40 25.85 0.60 4.99 0.80 1.52 0.22 284.36 0.42 21.23 0.62 4.37 0.82 1.37 0.24 200.71 0.44 17.60 0.64 3.83 0.84 1.24 0.26 145.66 0.46 14.71 0.66 3.38 0.86 1.12 0.28 108.24 0.48 12.38 0.68 2.99 0.88 1.02 Table 1. Additional stress coefficient under circular uniform distribution load
-
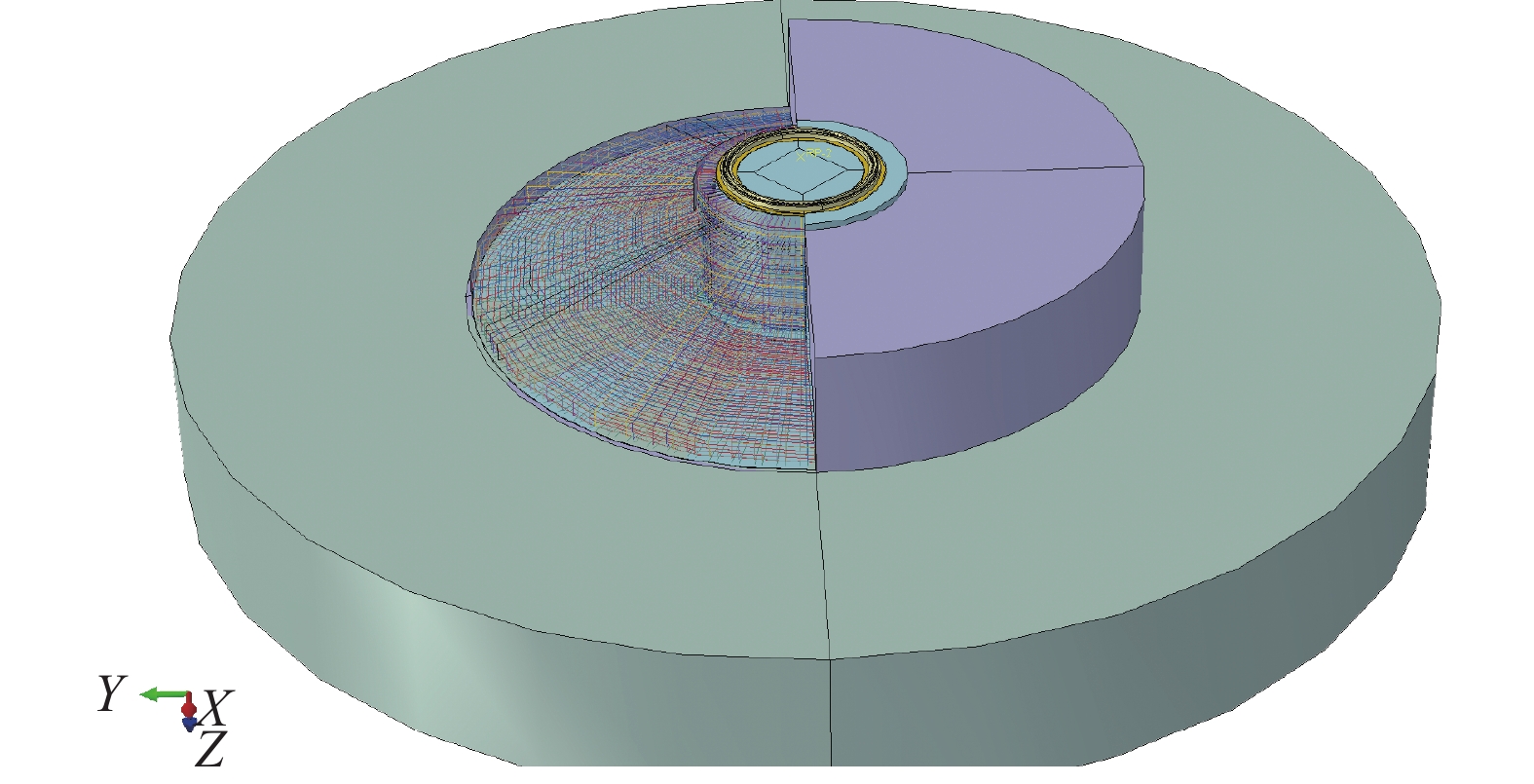
本研究利用大型通用有限元分析软件ABAQUS 对混凝土、钢筋、锚栓组合件及地基土进行一体化建模分析及计算。其中混凝土、锚栓组合件、地基土采用C3D8R实体单元进行模拟，钢筋采用T3D2杆单元进行模拟，模型最大单元尺寸不超过0.1 m。
模型组装模型如图4所示。
Figure 4. Fan foundation assembly model
-
模型材料包含混凝土、钢筋、锚栓组合件及地基土，由于本次分析为探寻核心区的应力分布规律，故材料本构模型均采用弹性模型，本构模型参数的标定参照《混凝土结构设计规范》即文献[2]确定。
-
有限元基础模型中主体混凝土与锚板、混凝土与地基土、锚板与锚栓之间施加面与面的库伦接触约束。其法向传递压力，切向传递摩擦力,选用小范围滑动，接触缝隙容差为0。摩擦系数设置为各向同性,钢与混凝土之间取0.3，混凝土与混凝土之间取0.4，混凝土与岩石层之间取0.4。
-
为了保证有限元结果准确性，本文建立细致的有限元分析模型如图5所示，并对部分单元格进行加密，单个单元格大小小于0.05 m，以保证分析结果准确性。
Figure 5. Detailed foundation model schematic (partial)
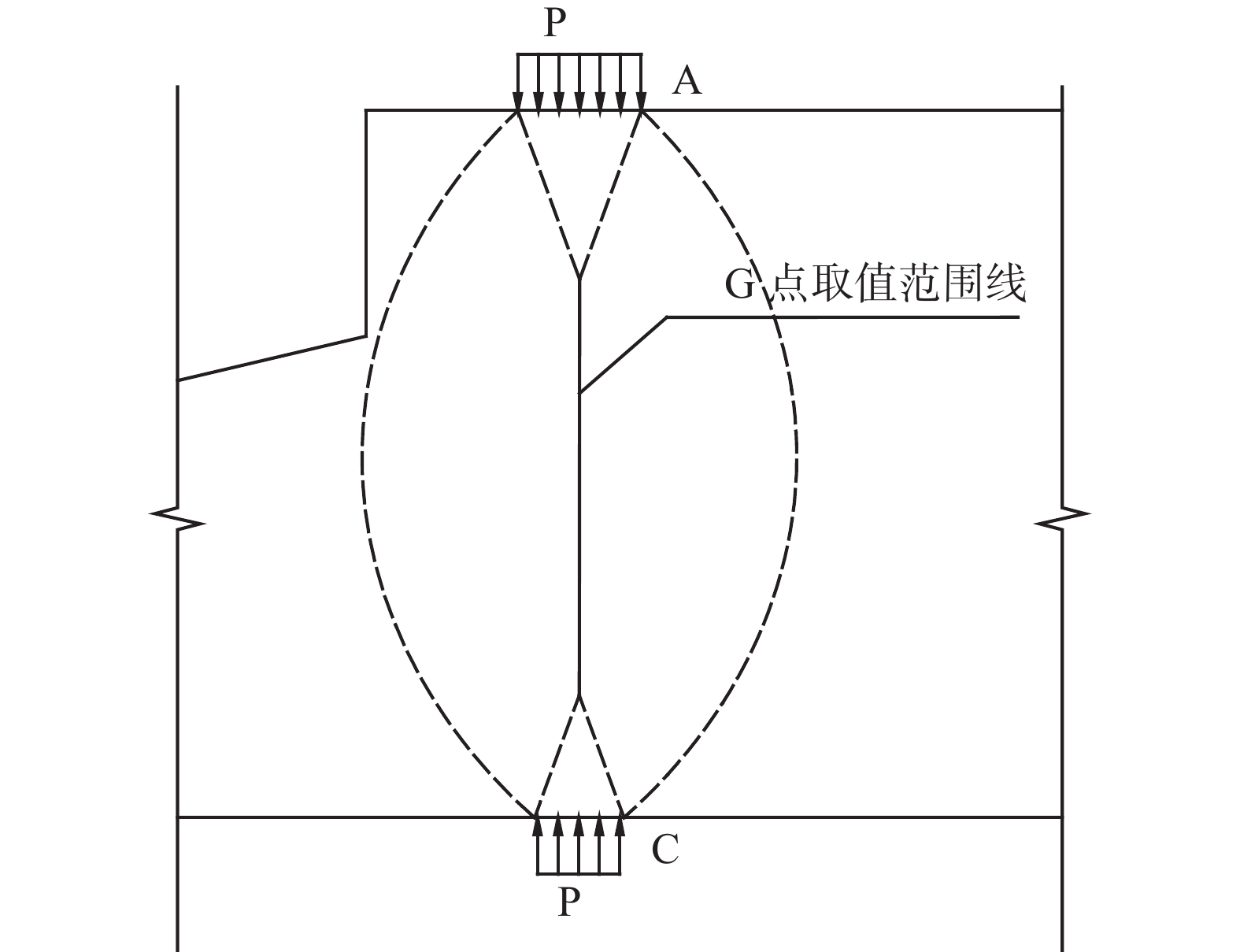
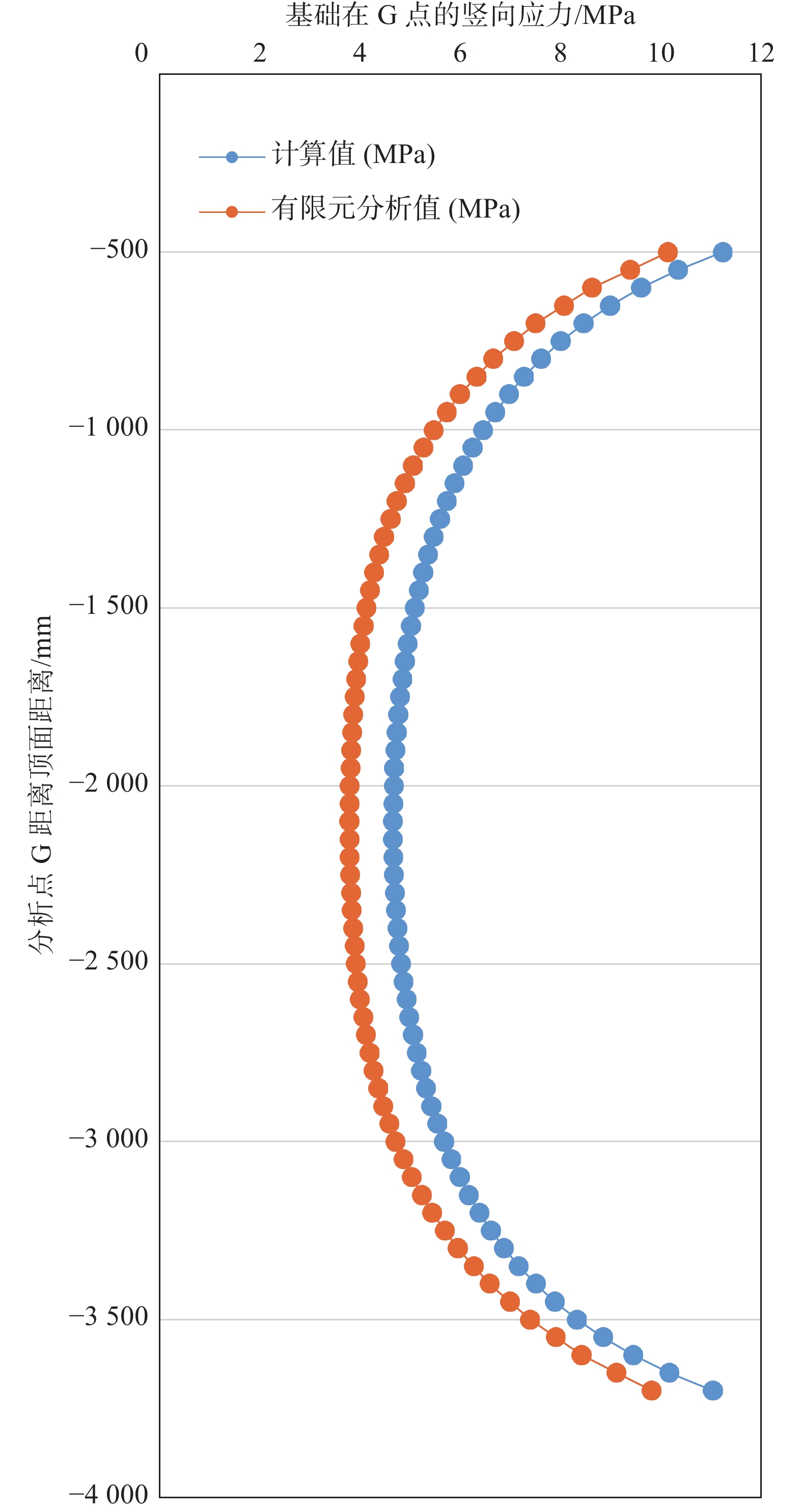
为章节1的分析结论，通过有限元分析计算G点的应力结果，G点的取值范围为章节1所提到的弹性体区域范围，位于局部荷载的中线位置。G点范围示意图如图6所示，有限元分析结果如表2所示。
Figure 6. G point value range diagram
计算点深度/
mm计算值/
MPa有限元分析值/
MPa计算值/有限元分析值
的比值500 −11.23 −10.14 1.11 550 −10.34 −9.38 1.10 600 −9.60 −8.63 1.11 650 −8.98 −8.06 1.11 700 −8.46 −7.50 1.13 750 −8.00 −7.07 1.13 800 −7.61 −6.65 1.14 850 −7.26 −6.32 1.15 900 −6.96 −5.98 1.16 950 −6.69 −5.73 1.17 1 000 −6.45 −5.47 1.18 1 050 −6.24 −5.26 1.19 1 100 −6.05 −5.05 1.20 1 150 −5.88 −4.89 1.20 1 200 −5.73 −4.73 1.21 1 250 −5.59 −4.60 1.22 1 300 −5.47 −4.47 1.22 1 350 −5.35 −4.37 1.22 1 400 −5.25 −4.27 1.23 …… …… …… …… 2 750 −5.13 −4.19 1.22 2 800 −5.21 −4.26 1.22 2 850 −5.31 −4.36 1.22 2 900 −5.42 −4.46 1.22 2 950 −5.54 −4.58 1.21 3 000 −5.67 −4.71 1.21 3 050 −5.82 −4.87 1.20 3 100 −5.98 −5.03 1.19 3 150 −6.17 −5.23 1.18 3 200 −6.38 −5.43 1.17 3 250 −6.61 −5.69 1.16 3 300 −6.87 −5.94 1.16 3 350 −7.16 −6.26 1.14 3 400 −7.50 −6.58 1.14 3 450 −7.88 −6.98 1.13 3 500 −8.33 −7.39 1.13 3 550 −8.84 −7.90 1.12 3 600 −9.45 −8.42 1.12 3 650 −10.16 −9.12 1.12 3 700 −11.03 −9.81 1.12 Table 2. Comparison table of calculation results
-
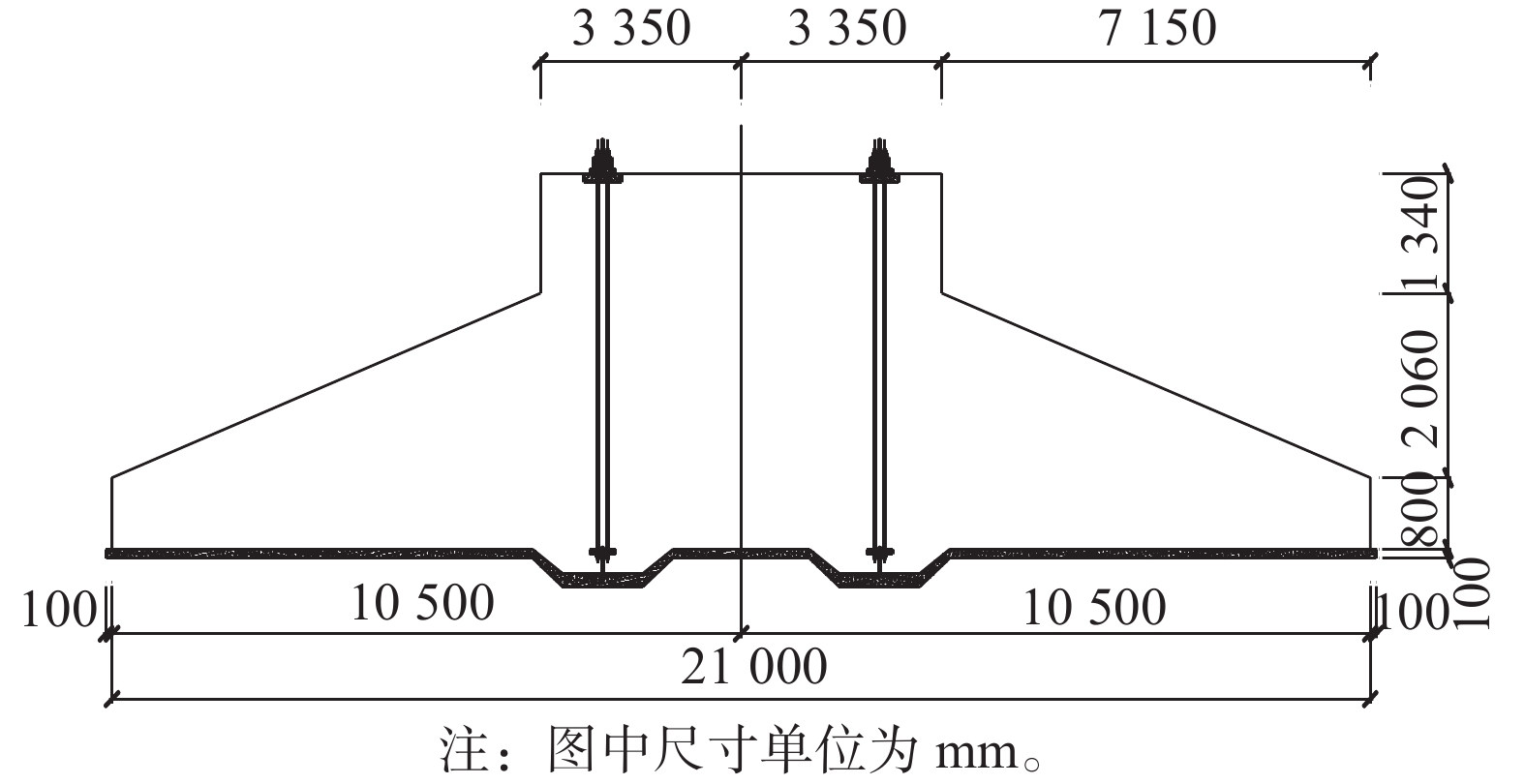
某项目风力发电机组单机容量为6.25 MW，轮毂高度110 m，叶轮直径183 m。塔筒与基础采用了预应力锚栓连接。地基承载力良好，采用重力扩展式基础。
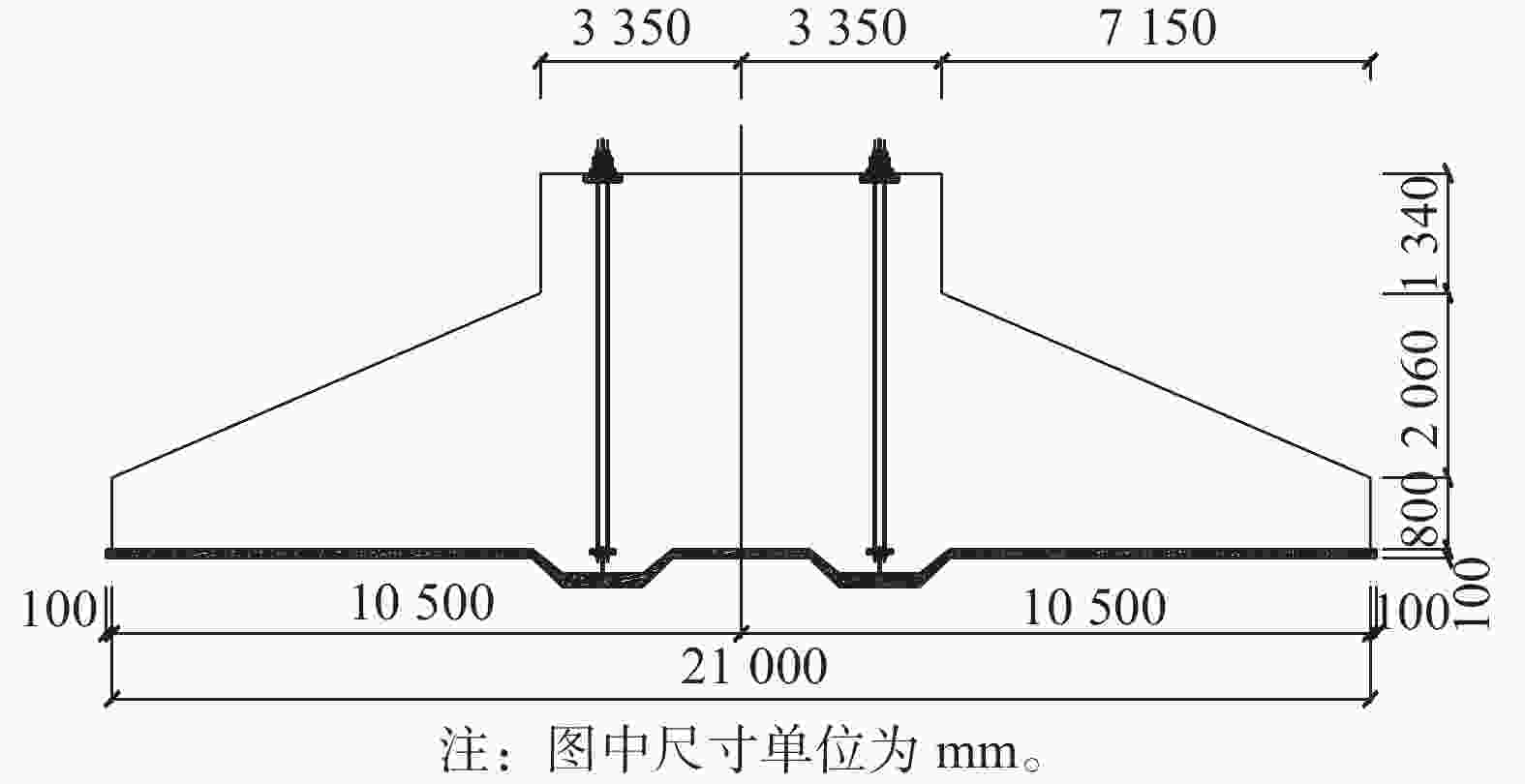
风机基础主体混凝土强度等级为C40，钢筋主筋强度等级HRB400。设计安全等级为一级，基础底板直径为21 m，基础总高度为4.25 m，台柱直径为6.7 m，台柱高度为1.34 m，基础悬挑根部高度为2.86 m，基础边缘高度为0.8 m，基础埋深为3.8 m。塔筒底法兰通过192根M42的锚栓与基础连接，锚栓设计预拉力为617 kN，超张拉系数为1.15。上锚板半径尺寸为2 152~2 508 mm，宽度为356 mm。下锚板半径尺寸为2 112~2 546 mm，宽度为434 mm。
风机基础外形尺寸如图7所示。
Figure 7. External dimension diagram of fan foundation
风机基础受力分析复杂，同时受到锚栓预应力，及上部风力发电机组传给基础的弯矩，竖向力，扭矩及水平力，为方便解释本文理念，本文给出仅考虑锚栓预应力作用的计算示例。
对此可以通过先求解基础所受最大压应力数值，代入本文公式进行计算，进一步的进行风机基础核心区竖向钢筋的配筋计算。
根据公式（8），求得上下锚板间楔形体高度分别为372 mm，449 mm，取为500 mm，即锚板之间500 mm范围内的混凝土不采用弹性理论计算基础应力。
参照文献[7]所示计算过程首先求得上锚板压应力:
$$ {p_1} = 24.50\;{\text{MPa}} $$ 下锚板压应力:
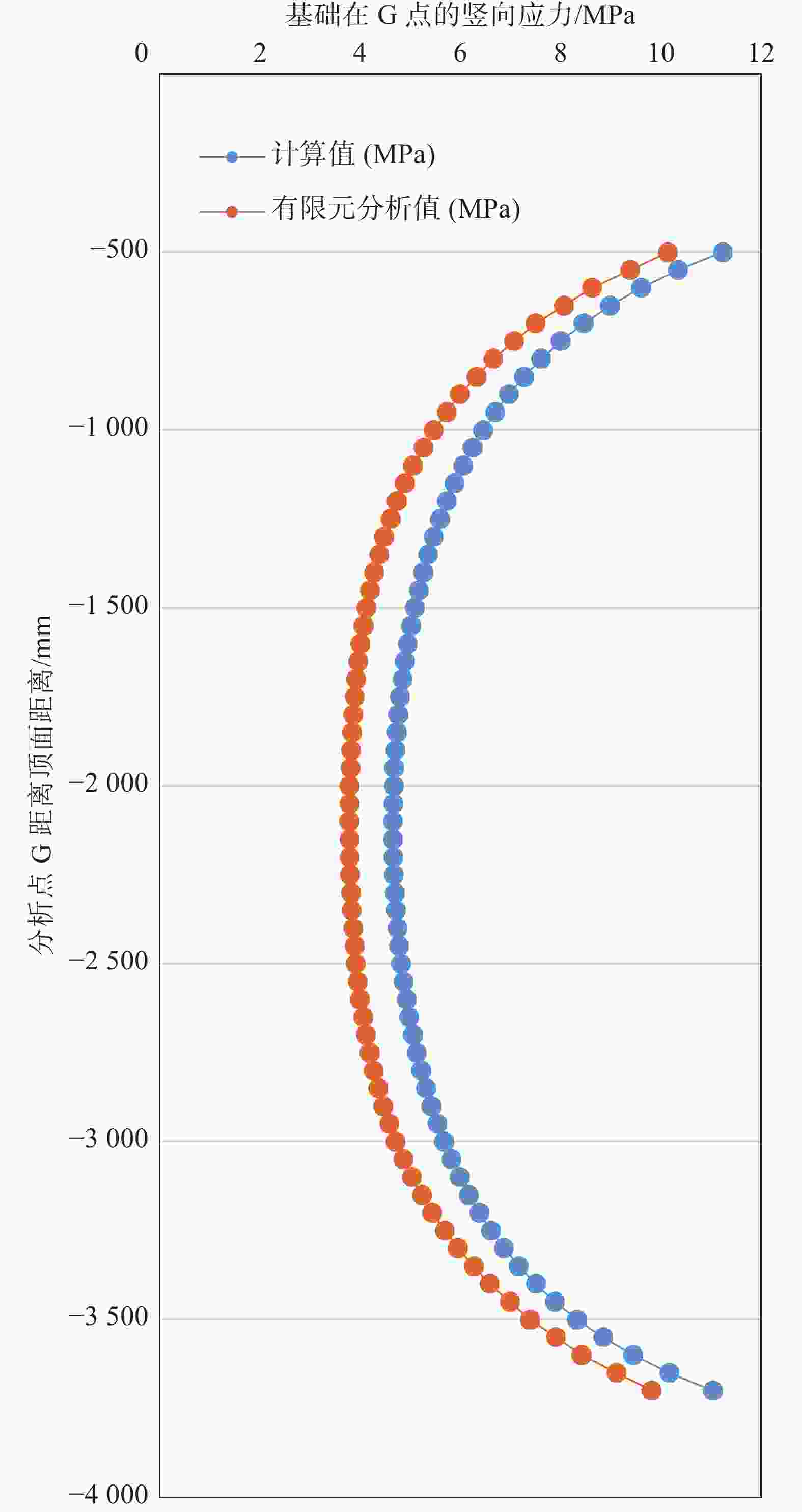
$$ {p_2} = 19.83\;{\text{MPa}} $$ 根据式（17）及表1求得基础在0.5~3.7 m范围（取值点位置同图6 所示:G点取值范围示意图）内竖向附加应力如表2及图8所示。
Figure 8. Comparison of calculation results
通过与精细的有限元模型结果对比，本文提出的非楔形体的应力计算公式是偏于安全，高于有限元分析值10%~25%，且应力差值维持在0.95~1.1 MPa，这是由于式（16）为简化计算而放大了环向荷载的应力效应导致的，是可以为工程设计所接受的。
-
1)风机基础核心区的应力状态可分为楔形体部分和非楔形体部分，楔形体部分混凝土不会发生受压破坏，非楔形体部分通过弹性力学的方法求解应力大小。
2)通过与精细的有限元模型结果对比，本文提出的非楔形体的应力计算公式是偏于安全，高于有限元分析值10%~25%，是可以为工程设计所接受的。这是由于式（16）为简化计算而放大了环向荷载的应力效应导致的。在有经验的前提下，可以考虑通过增加折减系数，来减少式（16）简化计算的影响。
3)风机基础在外荷载及预应力的共同作用下，荷载变化并不是均布的，而是随弯矩作用方向呈现线性分布规律，对此可以通过先求解基础所受最大压应力数值，代入本文公式进行计算，进一步的进行风机基础核心区竖向钢筋的配筋计算。
4)下一步研究可以通过求解微分单元下的竖向力F与x的方程。并带入公式（16）求解。
Research on Vertical Stress Law of Fan Foundation Under Annular Uniform Load
doi: 10.16516/j.ceec.2024.S1.20
- Received Date: 2024-03-21
- Rev Recd Date: 2024-04-18
- Publish Date: 2024-06-30
-
Key words:
- onshore wind turbine /
- foundation reinforcement /
- optimization design
Abstract:
| Citation: | LI Yuxiang, WU Qiang, MA Shen, et al. Research on vertical stress law of fan foundation under annular uniform load [J]. Southern energy construction, 2024, 11(Suppl. 1): 127-134. DOI： 10.16516/j.ceec.2024.S1.20 doi: 10.16516/j.ceec.2024.S1.20
|
DownLoad:
