-
磁场发生装置是一种产生一定区域均匀磁场的线圈结构，在线圈上通入电流可产生所需要的磁场，可用于受磁场干扰的器件的抗扰度测试，在生物医学[1]，传感器[2]、核聚变装置[3]以及其他场合的应用。
为了计算方便，对均匀磁场区域内部参数引入以下参数：
1）均匀区域尺寸（2s，m）：正方形均匀区域的边长。
2）最小磁感应强度（Bmin，mT）：均匀区域内磁场感应强度的最小值。
3）最大磁感应强度（Bmax，mT）：均匀区域内磁场感应强度的最大值。
4）磁场均匀性（η）：最大和最小磁感应强度的比值。
$$ \eta = \dfrac{{{B_{\max }}}}{{{B_{\min }}}} $$ (1) 产生均匀磁场的装置结构很多，常用的有螺线管线圈[4]、Helmholtz线圈[5]和Maxwell线圈[6]，螺线管线圈是均匀磁场最理想的一种产生方式，其均匀度质量一般都很高，但是线圈尺寸有限，极大地限制了发展；Helmholtz线圈结构简单，但是均匀磁场区域较小[7]；Maxwell线圈是Helmholtz线圈的一种升级结构，均匀度较好，但是结构略复杂[8-9]；其他方式主要有多线圈组结构[10]，比如文献[11]提出使用半径相同的3组圆形线圈组；文献[12]提出了半径相同的4圆形线圈组；文献[13]提出了半径相同的8圆形线圈组；文献[14]对此类线圈进行综合分析，方法多种多样，也各有优劣。
由于方形结构在大型设备的制造和焊接过程中比圆形结构具有更多优势[15-16]，因此IEC（国际电工委员会）在磁场抗扰度试验中推荐了方形结构。本文着重对于Helmholtz线圈和Maxwell线圈两种方形线圈以及相应的优化结构进行分析计算，设计出更为合理的高均匀性磁场发生装置。
-
Helmholtz正方形线圈由同轴的两个正方形线圈组成。在文献[5]中对Helmholtz线圈及其优化结构进行了非常详细的分析，并以此为基础详细分析了误差因素的影响，但是仍然只是针对两线圈在磁场均匀度1.1~1.4范围内的研究，更多范围并没有延伸的分析。
Helmholtz线圈的距离是正方形线圈边长的0.544 5倍，其在中心2s×2s×2s测试区域产生的磁场均匀度为1.1，最小磁感应强度为250 mT的条件下，所用材料及空间体积是否最小，此时并不能判断。所以对此结构进行优化分析，将结果进行对比来确定最优结构。
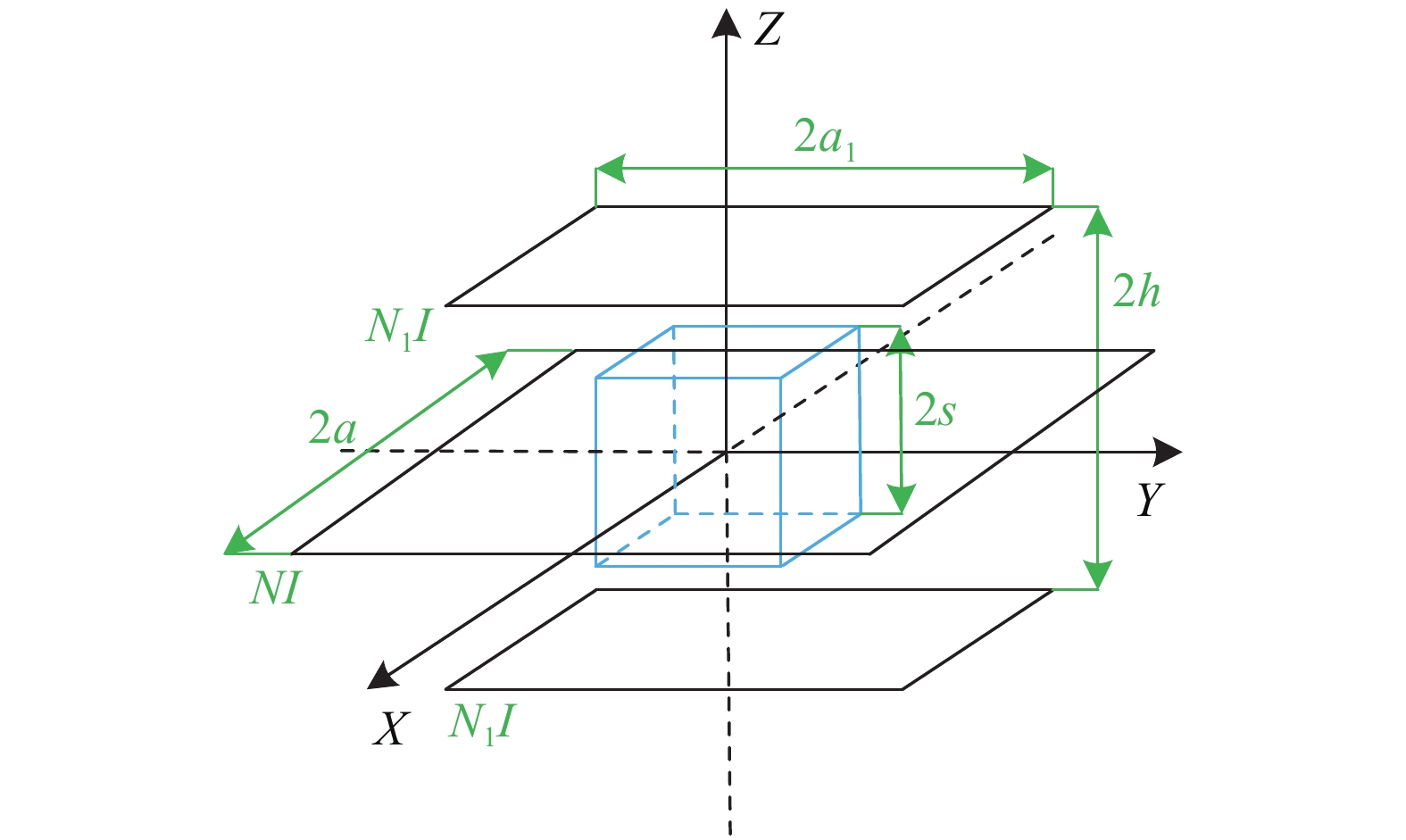
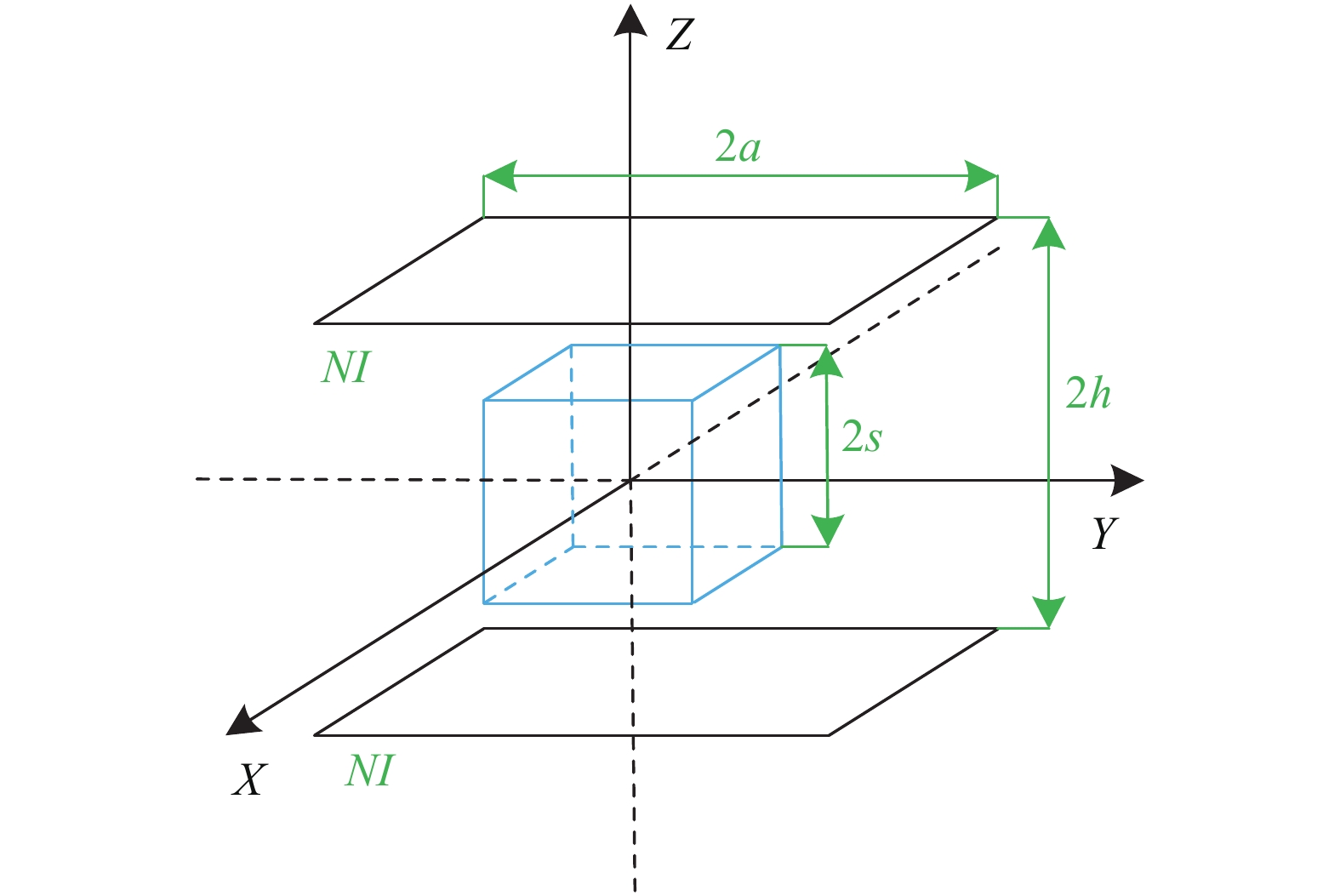
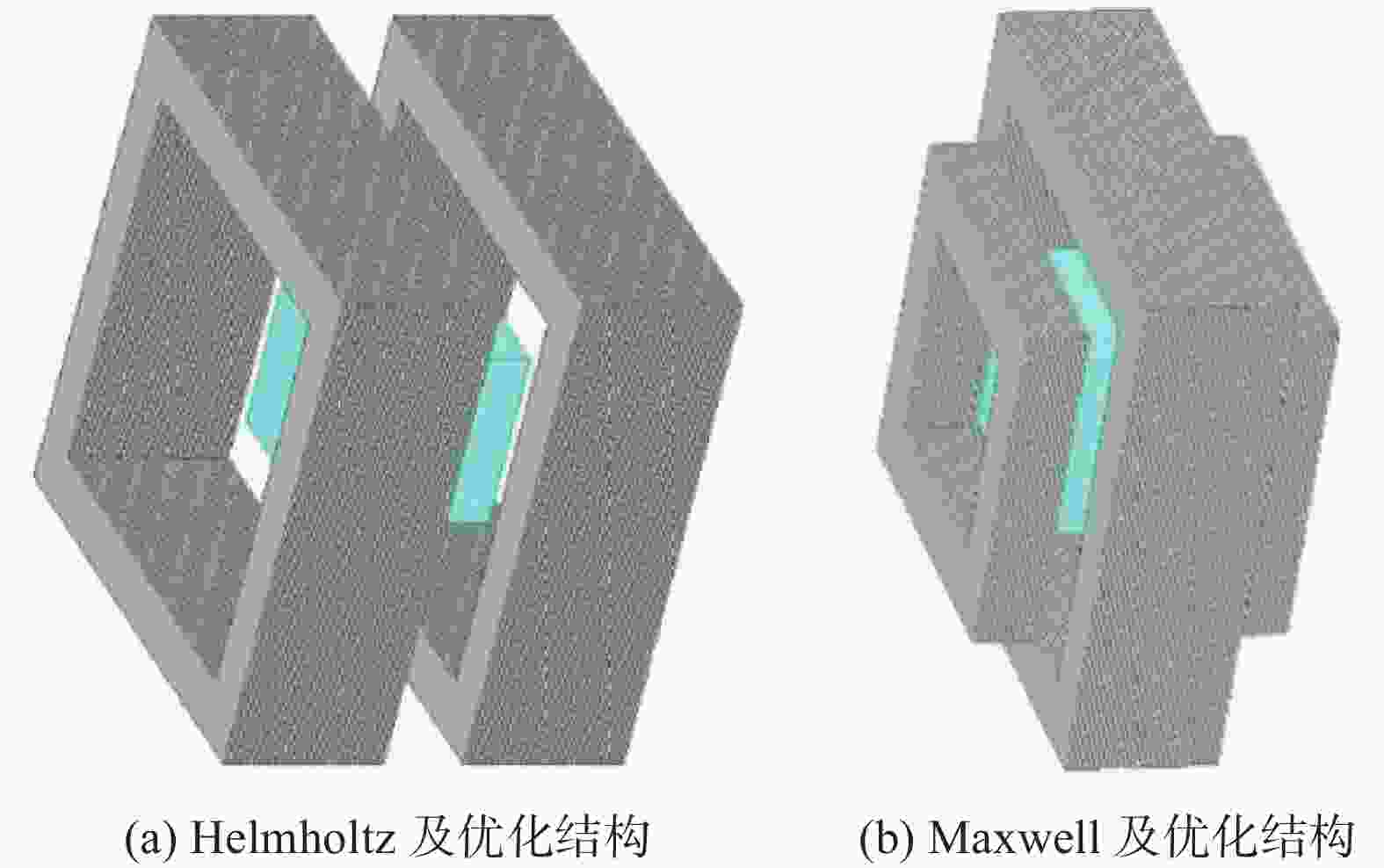
首先建立Helmholtz正方形线圈结构模型，如图1所示。磁场均匀区域位于坐标轴中心，边长为2s，正方形线圈边长为2a，两线圈的距离为2h，每组线圈的安匝数为NI（匝数为N，电流为I）。
Figure 1. Structural model of Helmholtz square coil
根据磁场叠加原理，得到线圈在测试区域任一点P(x, y,
$ z $ )上产生的轴向磁场为：$$ \begin{gathered} {B_z} = {B_z}\left( {x,y,z} \right) = \dfrac{{{\mu _0}NI}}{{4\text{π}}} \times \\ \left( \begin{gathered} \mathop \sum \limits_{i = 0}^1 \mathop \sum \limits_{j = 0}^1 \frac{{\left[ {{{\left( { - 1} \right)}^i}x + a} \right]\left[ {{{\left( { - 1} \right)}^j}y + a} \right]}}{{\sqrt {{{\left[ {{{\left( { - 1} \right)}^i}x + a} \right]}^2} + {{\left[ {{{\left( { - 1} \right)}^j}y + a} \right]}^2} + {{\left( {z - h} \right)}^2}} }} \times \\ \left[ {\frac{1}{{{{\left[ {{{\left( { - 1} \right)}^i}x + a} \right]}^2} + {{\left[ {z - h} \right]}^2}}} + \frac{1}{{{{\left[ {{{\left( { - 1} \right)}^j}y + a} \right]}^2} + {{\left( {z - h} \right)}^2}}}} \right] + \\ \mathop \sum \limits_{i = 0}^1 \mathop \sum \limits_{j = 0}^1 \frac{{\left[ {{{\left( { - 1} \right)}^i}x + a} \right]\left[ {{{\left( { - 1} \right)}^j}y + a} \right]}}{{\sqrt {{{\left[ {{{\left( { - 1} \right)}^i}x + a} \right]}^2} + {{\left[ {{{\left( { - 1} \right)}^j}y + a} \right]}^2} + {{\left( {z{\text{ + }}h} \right)}^2}} }} \times \\ \left[ {\frac{1}{{{{\left[ {{{\left( { - 1} \right)}^i}x + a} \right]}^2} + {{\left( {z{\text{ + }}h} \right)}^2}}} + \frac{1}{{{{\left[ {{{\left( { - 1} \right)}^j}y + a} \right]}^2} + {{\left( {z{\text{ + }}h} \right)}^2}}}} \right] \\ \end{gathered} \right) \\ \end{gathered} $$ (2) 式中：
μ0——真空磁导率；
$$ \left| x \right| \leqslant s,\;\left| y \right| \leqslant s,\left| z \right| \leqslant s。$$ 为简化计算，将测试区域归一化，即令:
$$ \left\{ \begin{gathered} u = {x \mathord{\left/ {\vphantom {x s}} \right. } s} \\ v = {y \mathord{\left/ {\vphantom {y s}} \right. } s} \\ w = {z \mathord{\left/ {\vphantom {z s}} \right. } s} \\ \end{gathered} \right. $$ (3) 代入式(2)，有：
$$ \begin{gathered} {B_z} = {B_z}\left( {u,v,w} \right) = \frac{{{\mu _0}}}{{4\text{π}}} \times \dfrac{{NI}}{s} \times \\ \left( \begin{gathered} \mathop \sum \limits_{i = 0}^1 \mathop \sum \limits_{j = 0}^1 \dfrac{{\left[ {{{\left( { - 1} \right)}^i}u + \dfrac{a}{s}} \right]\left[ {{{\left( { - 1} \right)}^j}v + \dfrac{a}{s}} \right]}}{{\sqrt {{{\left[ {{{\left( { - 1} \right)}^i}u + \dfrac{a}{s}} \right]}^2} + {{\left[ {{{\left( { - 1} \right)}^j}v + \dfrac{a}{s}} \right]}^2} + {{\left( {w - \dfrac{h}{s}} \right)}^2}} }} \times\\ \left[ \begin{gathered} \dfrac{1}{{{{\left[ {{{\left( { - 1} \right)}^i}u + \dfrac{a}{s}} \right]}^2} + {{\left( {w - \dfrac{h}{s}} \right)}^2}}} + \\ \dfrac{1}{{{{\left[ {{{\left( { - 1} \right)}^j}v + \dfrac{a}{s}} \right]}^2} + {{\left( {w - \dfrac{h}{s}} \right)}^2}}} \\ \end{gathered} \right] +\\ \mathop \sum \limits_{i = 0}^1 \mathop \sum \limits_{j = 0}^1 \dfrac{{\left[ {{{\left( { - 1} \right)}^i}u + \dfrac{a}{s}} \right]\left[ {{{\left( { - 1} \right)}^j}v + \dfrac{a}{s}} \right]}}{{\sqrt {{{\left[ {{{\left( { - 1} \right)}^i}u + \dfrac{a}{s}} \right]}^2} + {{\left[ {{{\left( { - 1} \right)}^j}v + \dfrac{a}{s}} \right]}^2} + {{\left( {w + \dfrac{h}{s}} \right)}^2}} }} \times\\ \qquad\qquad \left[ \begin{gathered} \dfrac{1}{{{{\left[ {{{\left( { - 1} \right)}^i}u + \dfrac{a}{s}} \right]}^2} + {{\left( {w + \dfrac{h}{s}} \right)}^2}}} + \\ \dfrac{1}{{{{\left( {{{\left[ { - 1} \right)}^j}v + \dfrac{a}{s}} \right]}^2} + {{\left( {w + \dfrac{h}{s}} \right)}^2}}} \\ \end{gathered} \right] \\ \end{gathered} \right) \\ \end{gathered} $$ (4) 式中：
$$ \left| u \right| \leqslant 1,\;\left| v \right| \leqslant 1,\left| w \right| \leqslant 1。 $$ 在测试区域内，磁感应强度最大值、最小值以及磁场均匀度是关于a/s、h/s、NI/s的函数，即
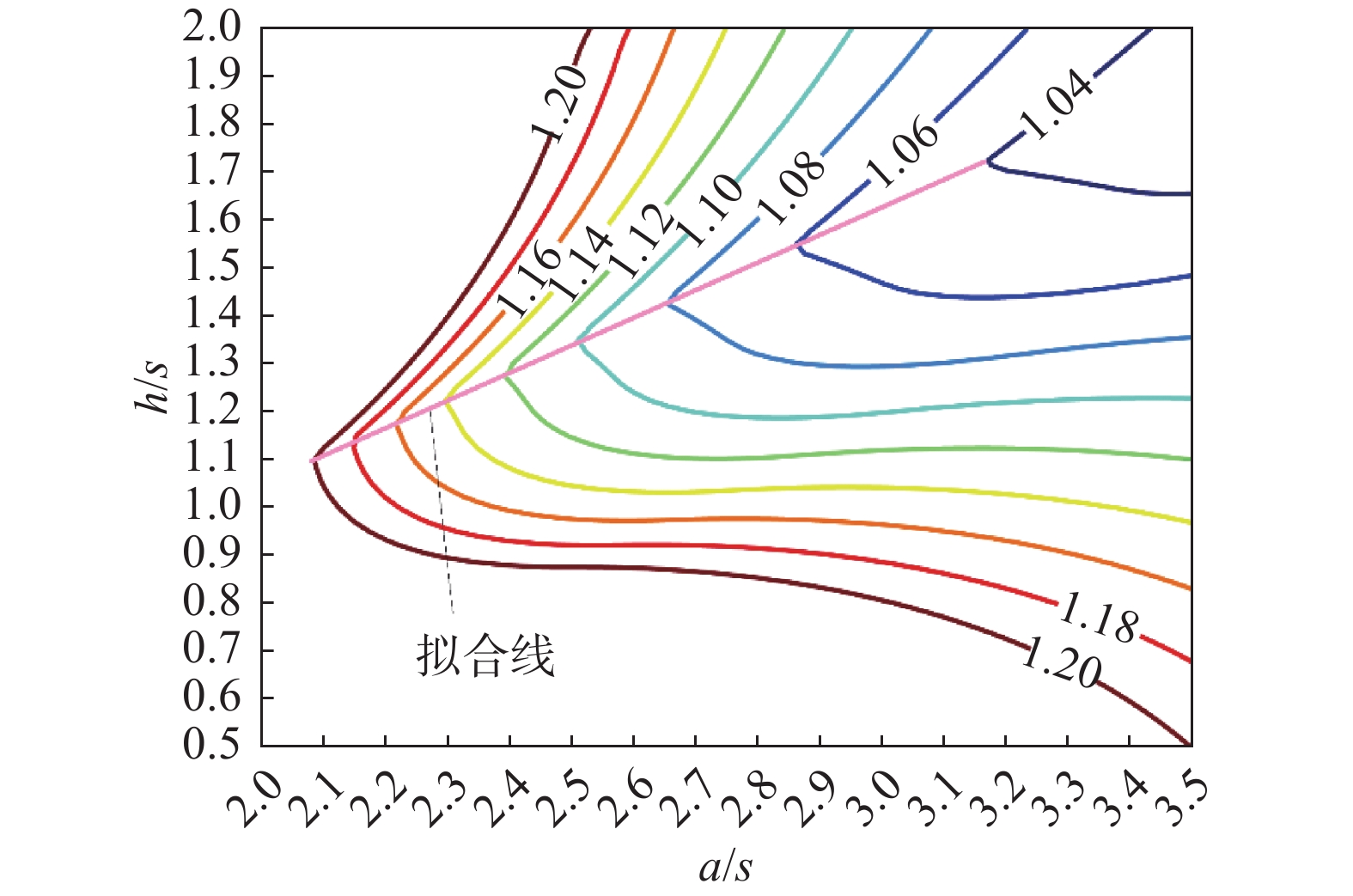
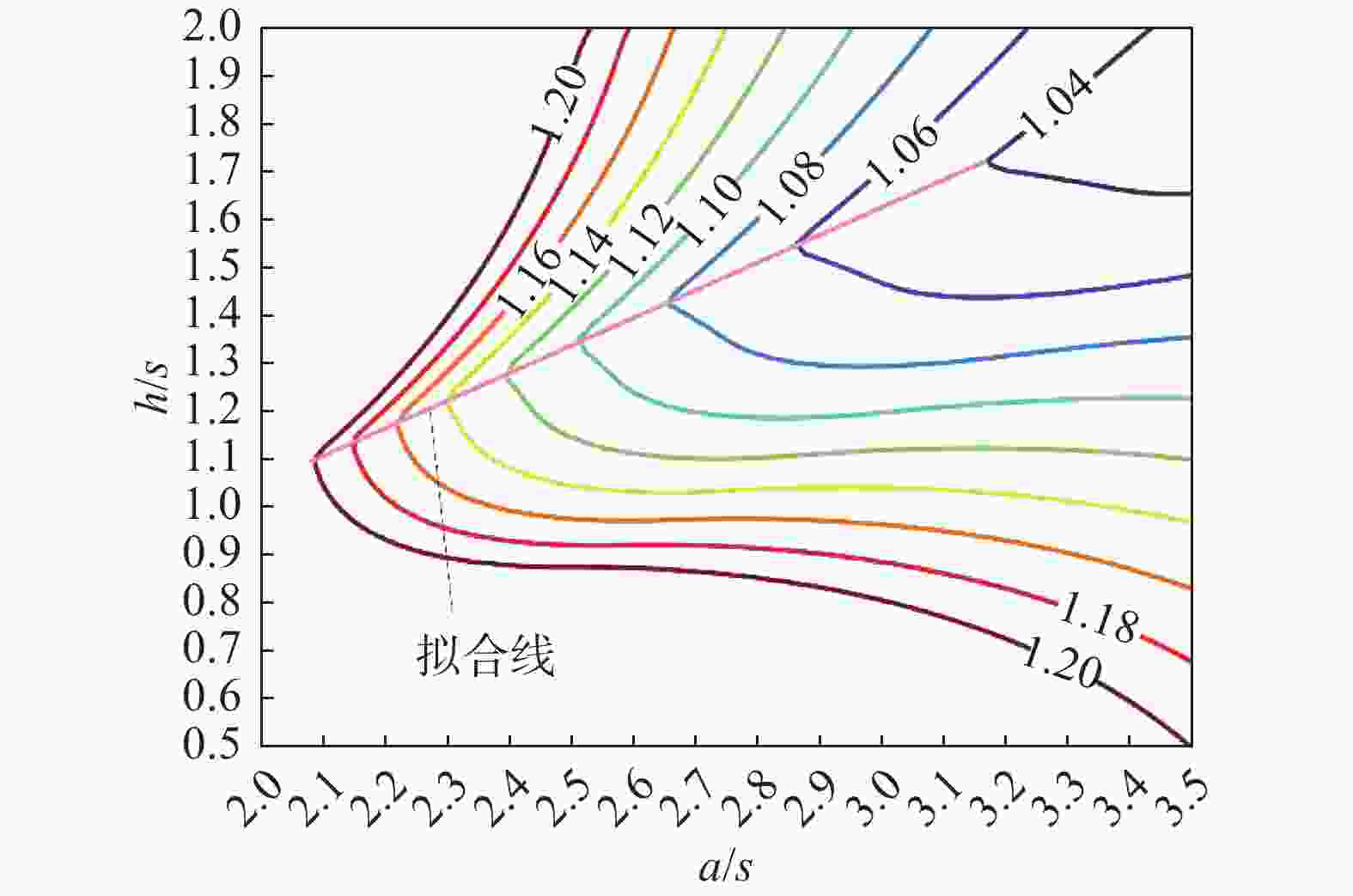
$$ \left\{ {\begin{array}{*{20}{c}} {{B_{{\rm{max}}}} = {f_1}\left( {\dfrac{a}{s},\dfrac{h}{s},\dfrac{{NI}}{s}} \right)} \\ {{B_{{\rm{min}}}} = {f_2}\left( {\dfrac{a}{s},\dfrac{h}{s},\dfrac{{NI}}{s}} \right)} \\ {\eta = f\left( {\dfrac{a}{s},\dfrac{h}{s}} \right)} \end{array}} \right. $$ (5) 通过数值计算分析，得到磁场均匀性η关于线圈尺寸参数a/s、h/s的分布，如图2所示。从图中可以看出，不同均匀度下的曲线均存在一个a/s最小点，此时线圈尺寸最小，耗材最少，结构最优。将这些a/s最小点连接成线（如图2所示直线），通过数值计算，进行曲线拟合，得到a/s、h/s关于η的近似表达式；再将Bmin=250 mT代入式(5)中，拟合出NI/s关于η的近似表达式，结果如下：
Figure 2. Distribution of magnetic field uniformity with size parameters
$$ \left\{ \begin{gathered} \frac{a}{s} = 1.941 + 6.217 \times {10^5}{{\rm{e}}^{ - 12.640\eta }} \\ \frac{h}{s} = 1.013 + 3.011 \times {10^5}{{\rm{e}}^{ - 12.470\eta }} \\ \frac{{NI}}{s} = 6.206 \times {10^5} + 4.391 \times {10^{11}}{{\rm{e}}^{ - 13.482\eta }} \\ \end{gathered} \right. $$ (6) 同时得到h关于a的近似表达式:
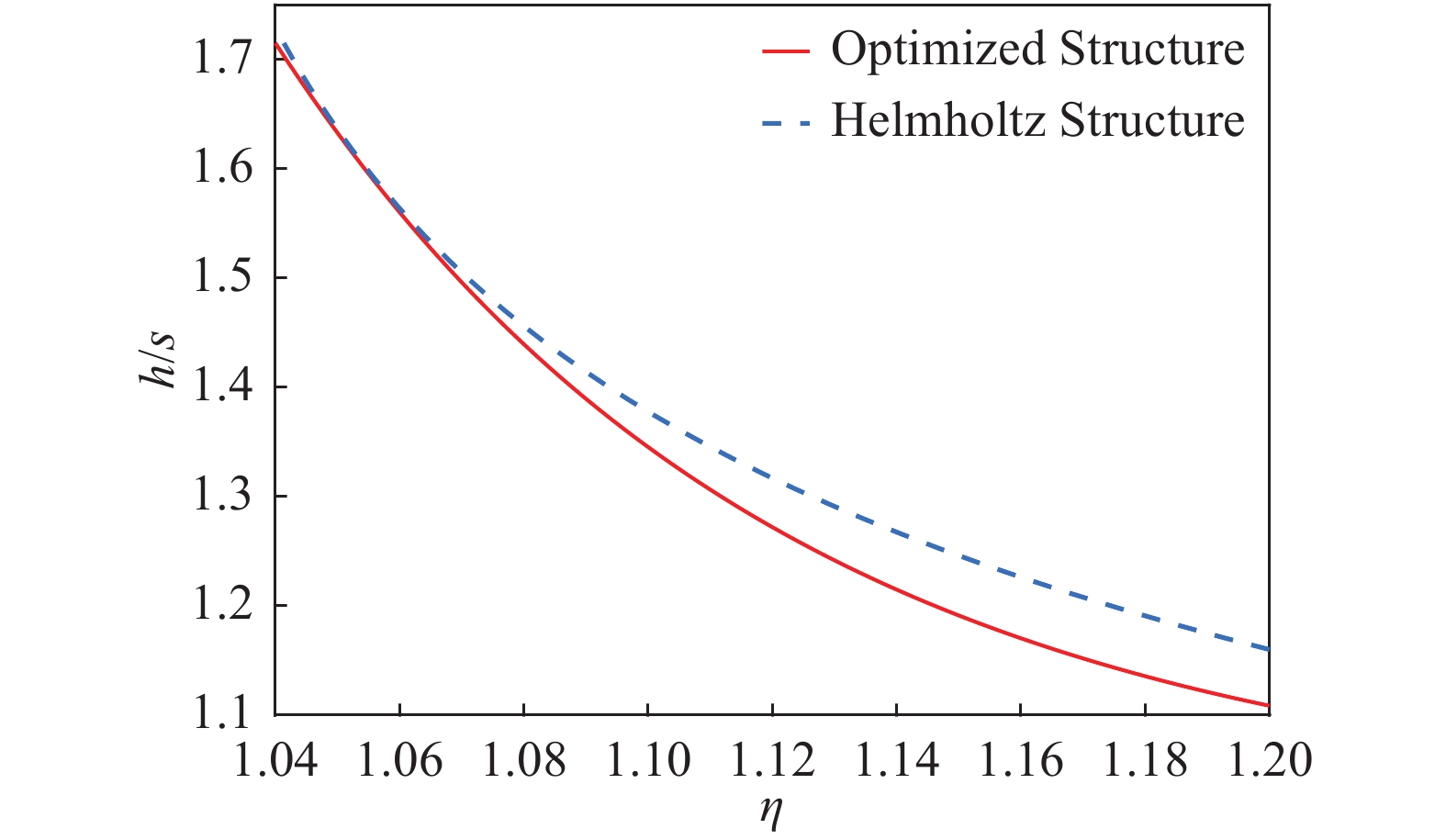
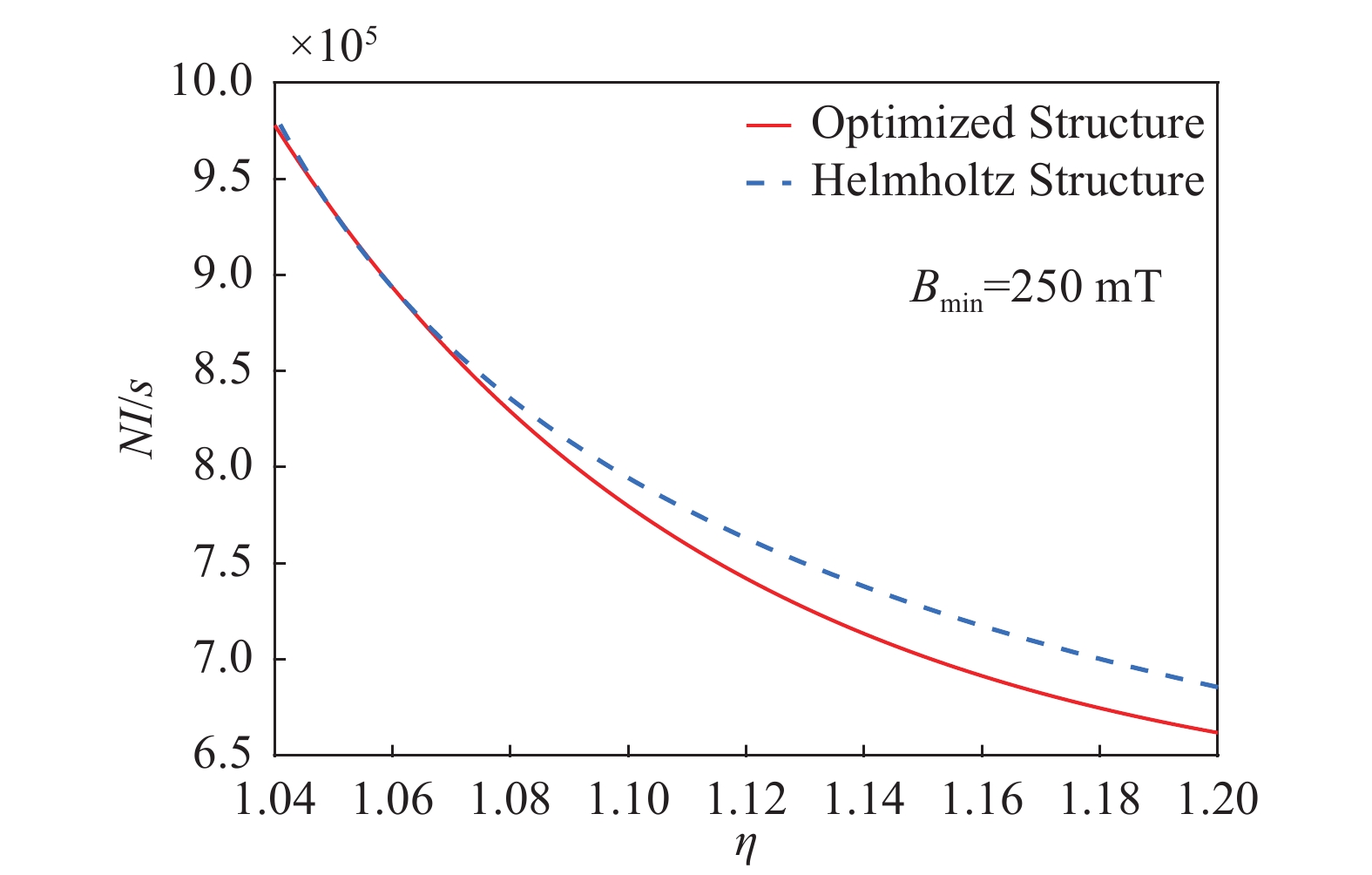
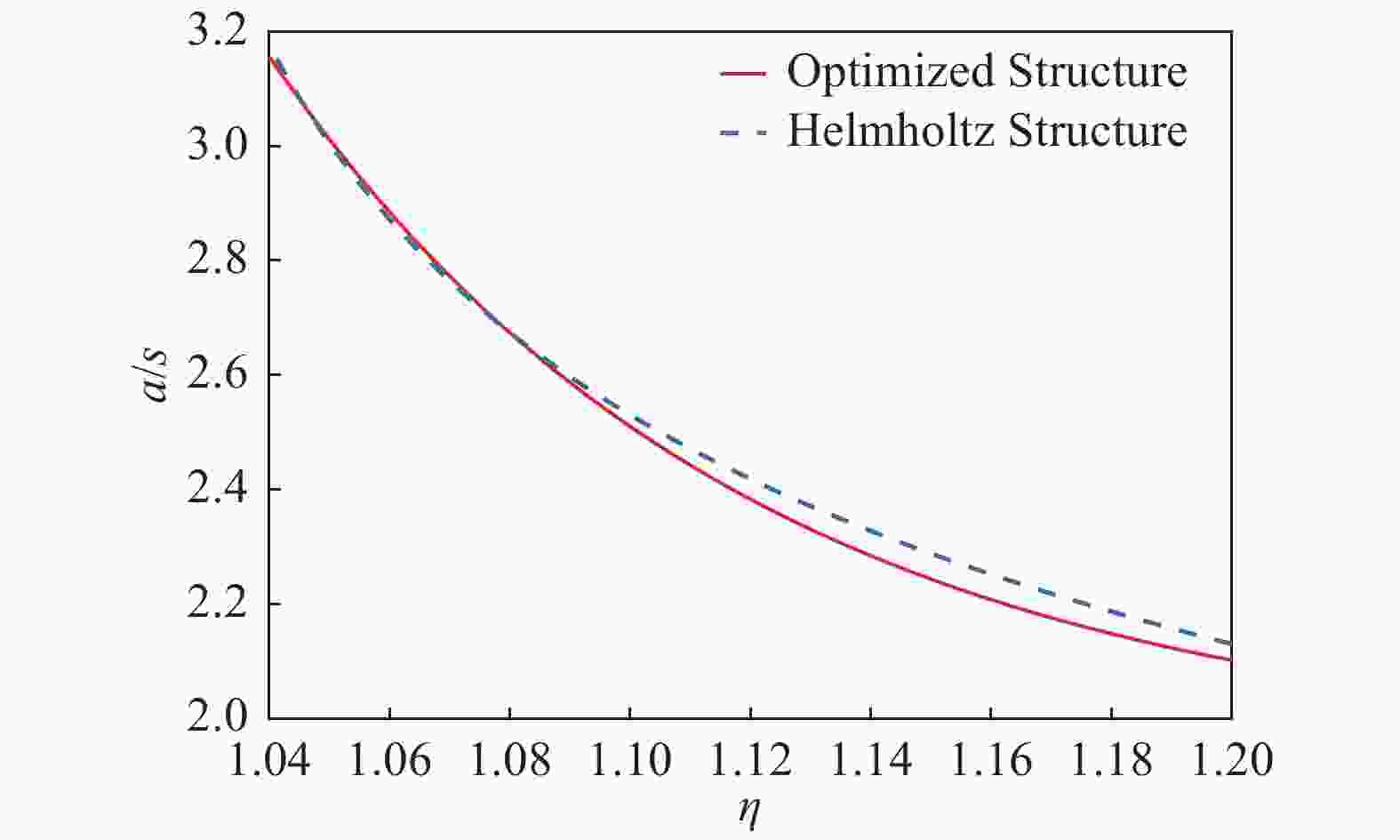
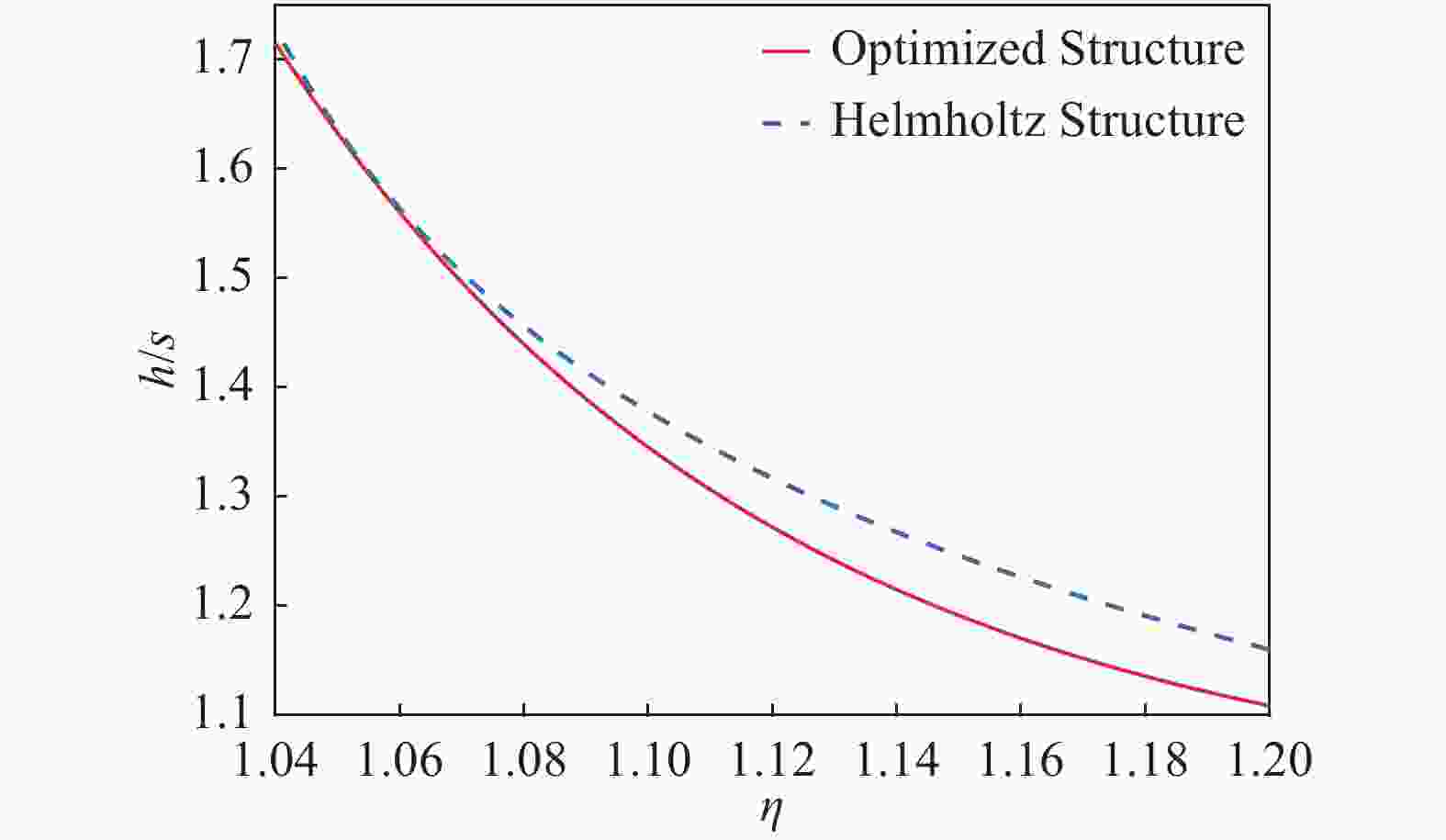
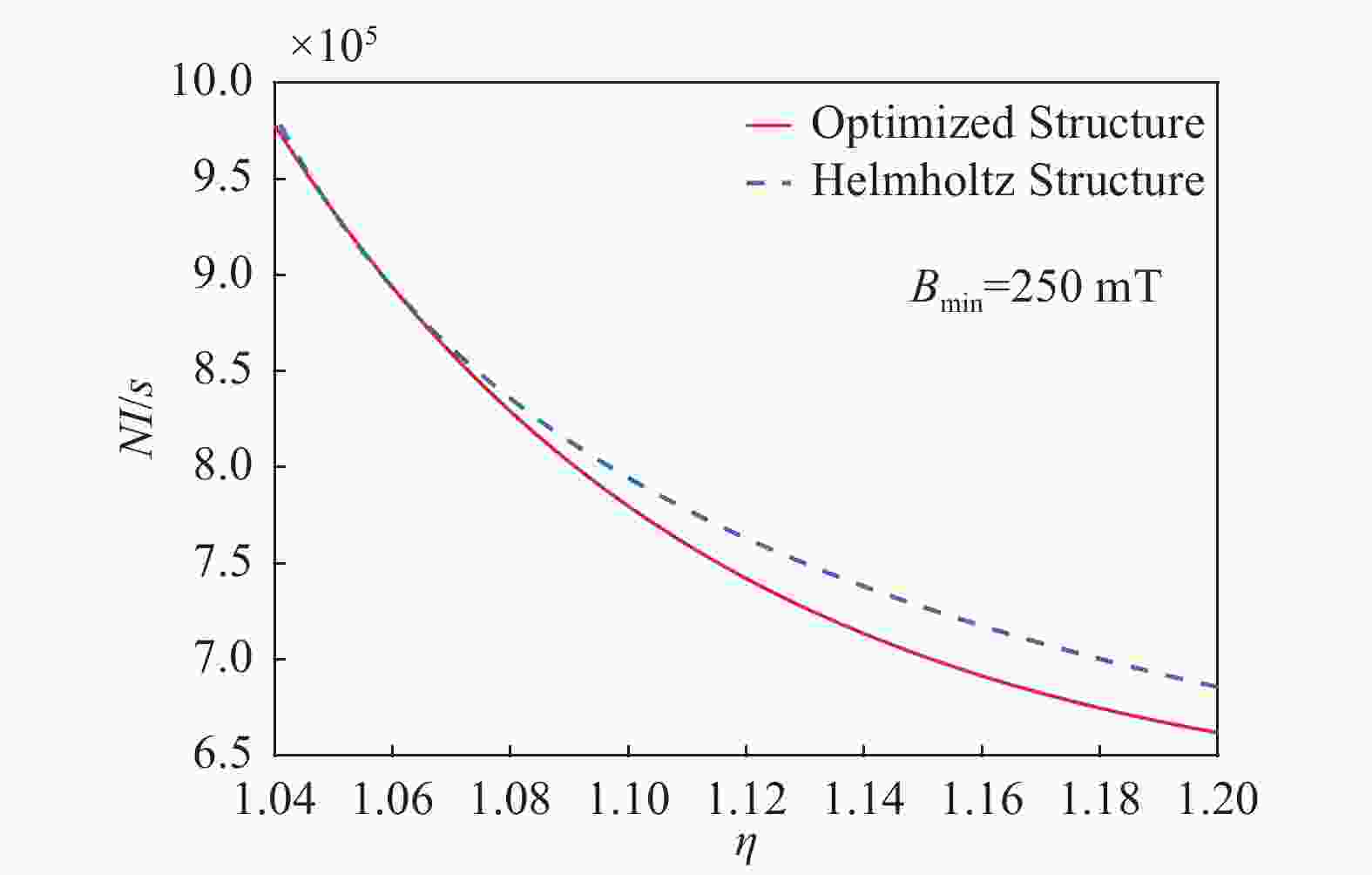
$$ h = 0.581a - 0.114s $$ (7) 绘制最优结构与Helmholtz结构(a=0.544 5h)时的a/s、h/s、NI/s与磁场均匀度的曲线分布，如图3、图4、图5所示。
Figure 3. Relationship between a/s and magnetic field uniformity
Figure 4. Relationship between h/s and magnetic field uniformity
Figure 5. Relationship between NI/s and magnetic field uniformity
从图中可以看出，在1 m×1 m×1 m测试空间内磁场均匀度η≥1.07时，优化结构相对于Helmholtz结构，尺寸更小，所需安匝数也更少。本文计算的结果忽略了截面效应，在后续研究中会继续深入分析，此处暂不考虑。
当η=1.1、Bmin=250 mT、s=0.5 m，计算得到Helmholtz结构与最优结构时的a、h、NI的值；再考虑输入电源电流I≤10 kA，求得两线圈的最小整数安匝比，如表1所示。可以看出，优化结构的体积更小，输入的电流也更小，成本更低。
参数 Helmholtz结构 优化结构 η 1.1 1.1 Bmin/mT 250 250 a/m 1.265 1.255 h/m 0.689 0.675 I/kA 9.93 9.76 N 40∶40 40∶40 Table 1. Parameter comparison between Helmholtz and optimized structure
-
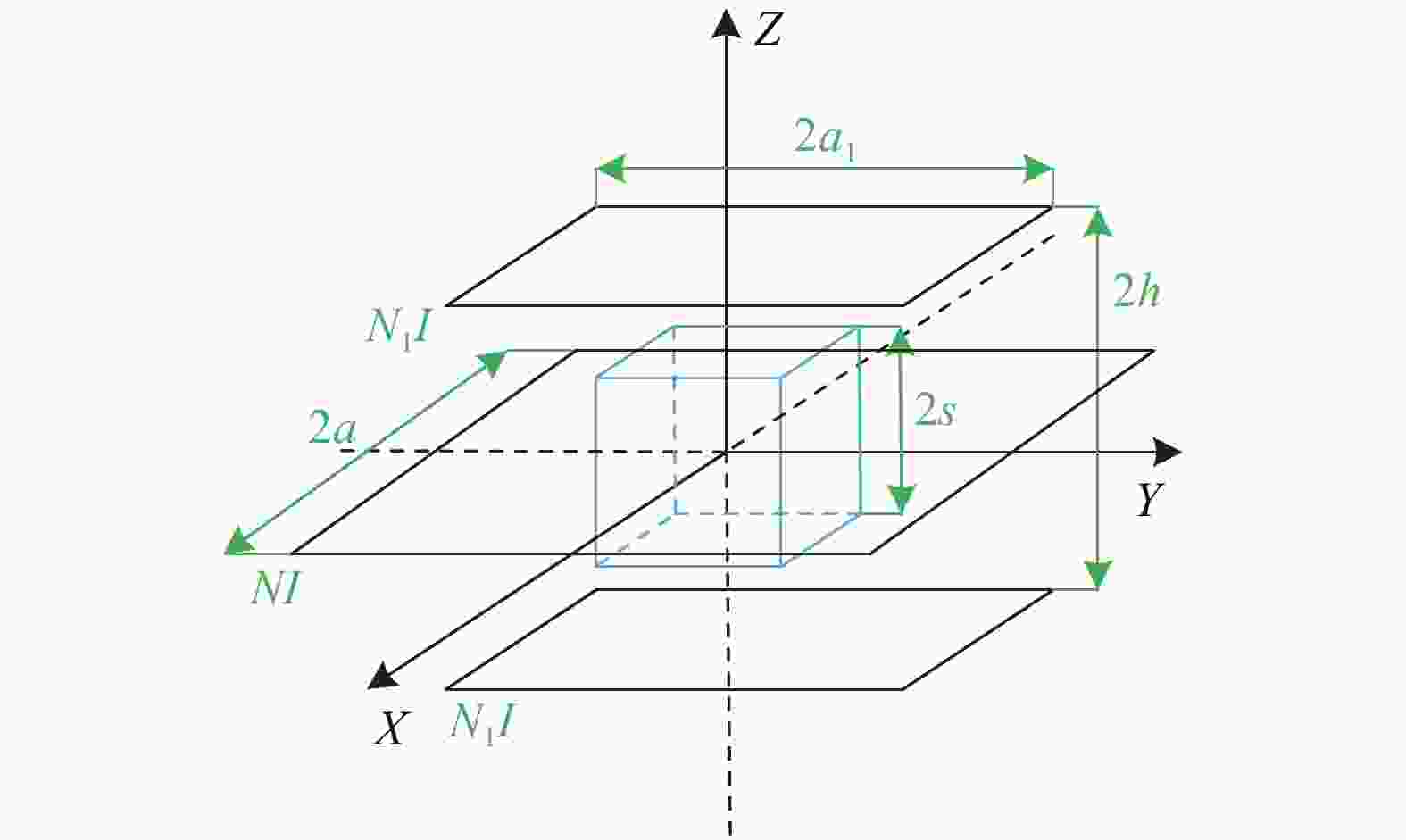
Maxwell正方形线圈由同轴的三个正方形线圈组成，结构模型如图6所示，需要利用泰勒展开式来确定Maxwell正方形线圈参数比例。
Figure 6. Structural model of Maxwell square coil
计算得到线圈组在点P(x, y, z)上产生的轴向磁场为：
$$ \begin{gathered} {B_z} = {B_z}\left( {x,y,z} \right) = \\ \frac{{{\mu _0}NI}}{{4\text{π} }}\mathop \sum \limits_{i = 0}^1 \mathop \sum \limits_{j = 0}^1 \frac{{\left[ {{{\left( { - 1} \right)}^i}x + a} \right]\left[ {{{\left( { - 1} \right)}^j}y + a} \right]}}{{\sqrt {{{\left[ {{{\left( { - 1} \right)}^i}x + a} \right]}^2} + {{\left[ {{{\left( { - 1} \right)}^j}y + a} \right]}^2} + {z^2}} }} \times\\ \left[ {\frac{1}{{{{\left[ {{{\left( { - 1} \right)}^i}x + a} \right]}^2} + {z^2}}} + \frac{1}{{{{\left[ {{{\left( { - 1} \right)}^j}y + a} \right]}^2} + {z^2}}}} \right] {\text{ + }}\\ \frac{{{\mu _0}{N_1}I}}{{4\text{π} }}\mathop \sum \limits_{i = 0}^1 \mathop \sum \limits_{j = 0}^1 \frac{{\left[ {{{\left( { - 1} \right)}^i}x + {a_1}} \right]\left[ {{{\left( { - 1} \right)}^j}y + {a_1}} \right]}}{{\sqrt {{{\left[ {{{\left( { - 1} \right)}^i}x + {a_1}} \right]}^2} + {{\left[ {{{\left( { - 1} \right)}^j}y + {a_1}} \right]}^2} + {{\left( {z{\text{ - }}h} \right)}^2}} }} \times\\ \left[ {\frac{1}{{{{\left[ {{{\left( { - 1} \right)}^i}x + {a_1}} \right]}^2} + {{\left( {z{\text{ - }}h} \right)}^2}}} + \frac{1}{{{{\left[ {{{\left( { - 1} \right)}^j}y + {a_1}} \right]}^2} + {{\left( {z{\text{ - }}h} \right)}^2}}}} \right] {\text{ + }}\\ \frac{{{\mu _0}{N_1}I}}{{4\text{π} }}\mathop \sum \limits_{i = 0}^1 \mathop \sum \limits_{j = 0}^1 \frac{{\left[ {{{\left( { - 1} \right)}^i}x + {a_1}} \right]\left[ {{{\left( { - 1} \right)}^j}y + {a_1}} \right]}}{{\sqrt {{{\left[ {{{\left( { - 1} \right)}^i}x + {a_1}} \right]}^2} + {{\left[ {{{\left( { - 1} \right)}^j}y + {a_1}} \right]}^2} + {{\left( {z{\text{ + }}h} \right)}^2}} }} \times\\ \left[ {\frac{1}{{{{\left[ {{{\left( { - 1} \right)}^i}x + {a_1}} \right]}^2} + {{\left( {z{\text{ + }}h} \right)}^2}}} + \frac{1}{{{{\left[ {{{\left( { - 1} \right)}^j}y + {a_1}} \right]}^2} + {{\left( {z{\text{ + }}h} \right)}^2}}}} \right] \\ \end{gathered} $$ (8) 根据上式，得到Z轴轴线上的磁场分布为
$$ \begin{array}{l}B(z)={B}_{z}\left(0,0,z\right)=\dfrac{{\mu }_{0}NI}{2\text{π} }\dfrac{{a}^{2}}{\left({a}^{2}+{z}^{2}\right)\sqrt{2{a}^{2}+{z}^{2}}} +\\\dfrac{{\mu }_{0}{N}_{1}I}{2\text{π} }\dfrac{{a}_{1}{}^{2}}{\left[ {a}^{2}+{\left(z-h\right)}^{2} \right]\sqrt{2{a}^{2}+{\left(z-h\right)}^{2}}} +\\\dfrac{{\mu }_{0}{N}_{1}I}{2\text{π} }\dfrac{{a}_{1}{}^{2}}{\left[ {a}_{1}{}^{2}+{\left(z+h\right)}^{2} \right]\sqrt{2{a}_{1}{}^{2}+{\left(z+h\right)}^{2}}}\end{array} $$ (9) Bz关于z=0对称，故当k为奇数时有Bk(0)=0，其在z=0处的泰勒展开式为：
$$ {B_z} = B(0){\text{ + }}\sum\limits_{k = 1}^\infty {{B^{2k}}(0)} \frac{{{z^{2k}}}}{{(2k)!}} $$ (10) 要产生理想的均匀磁场，则要求B(z)=B(0)，即要求B2k(0)=0，计算得到：
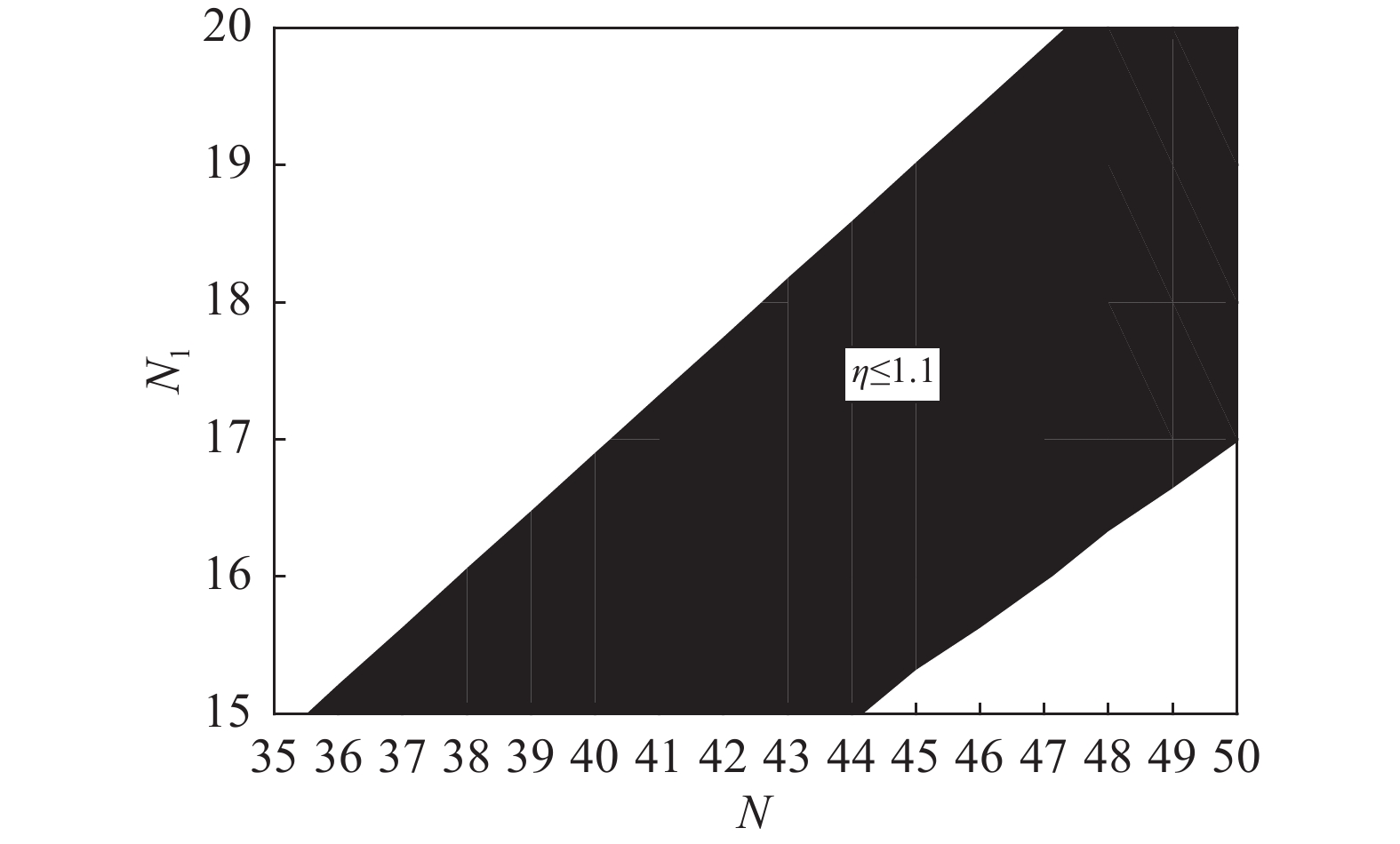
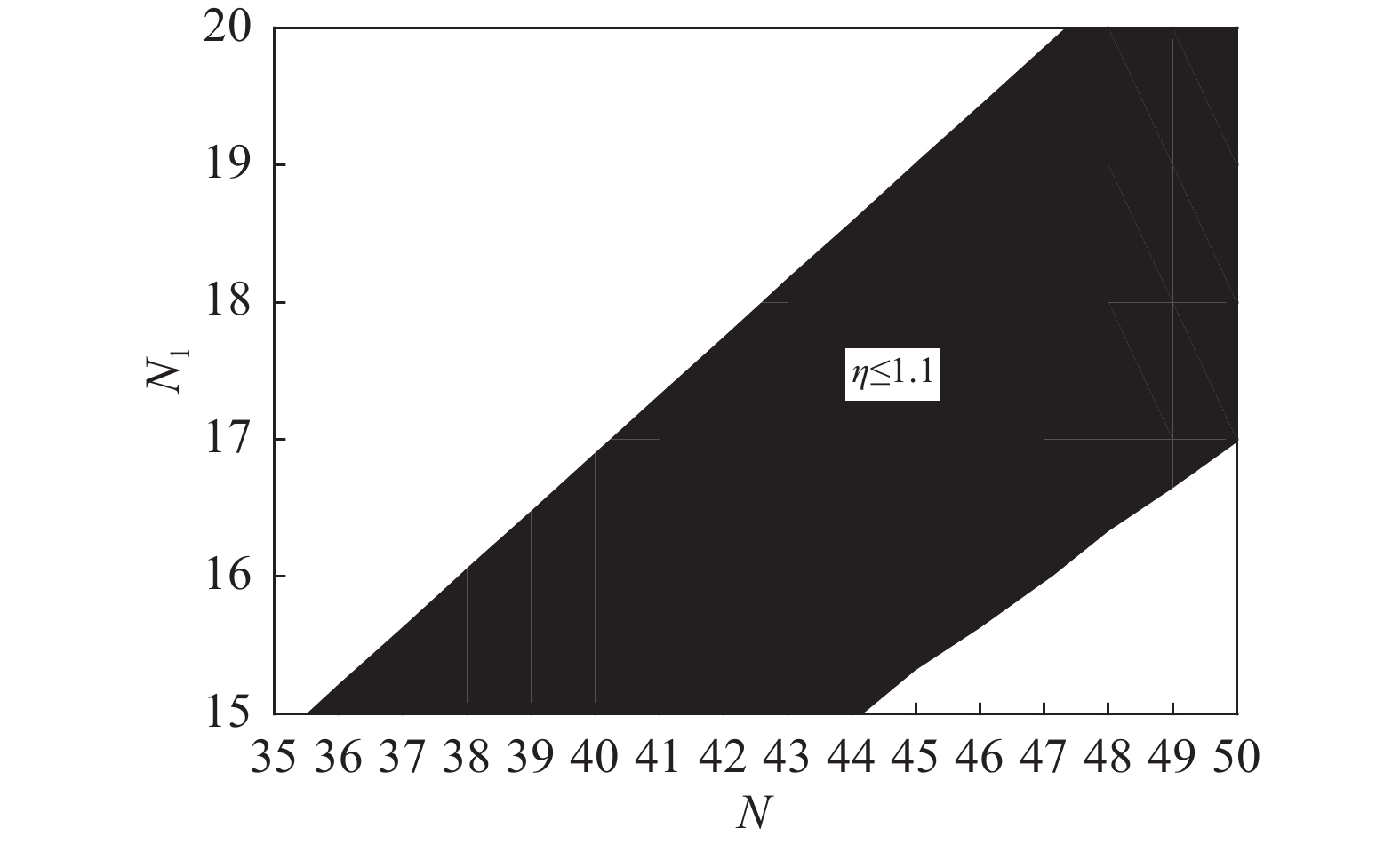
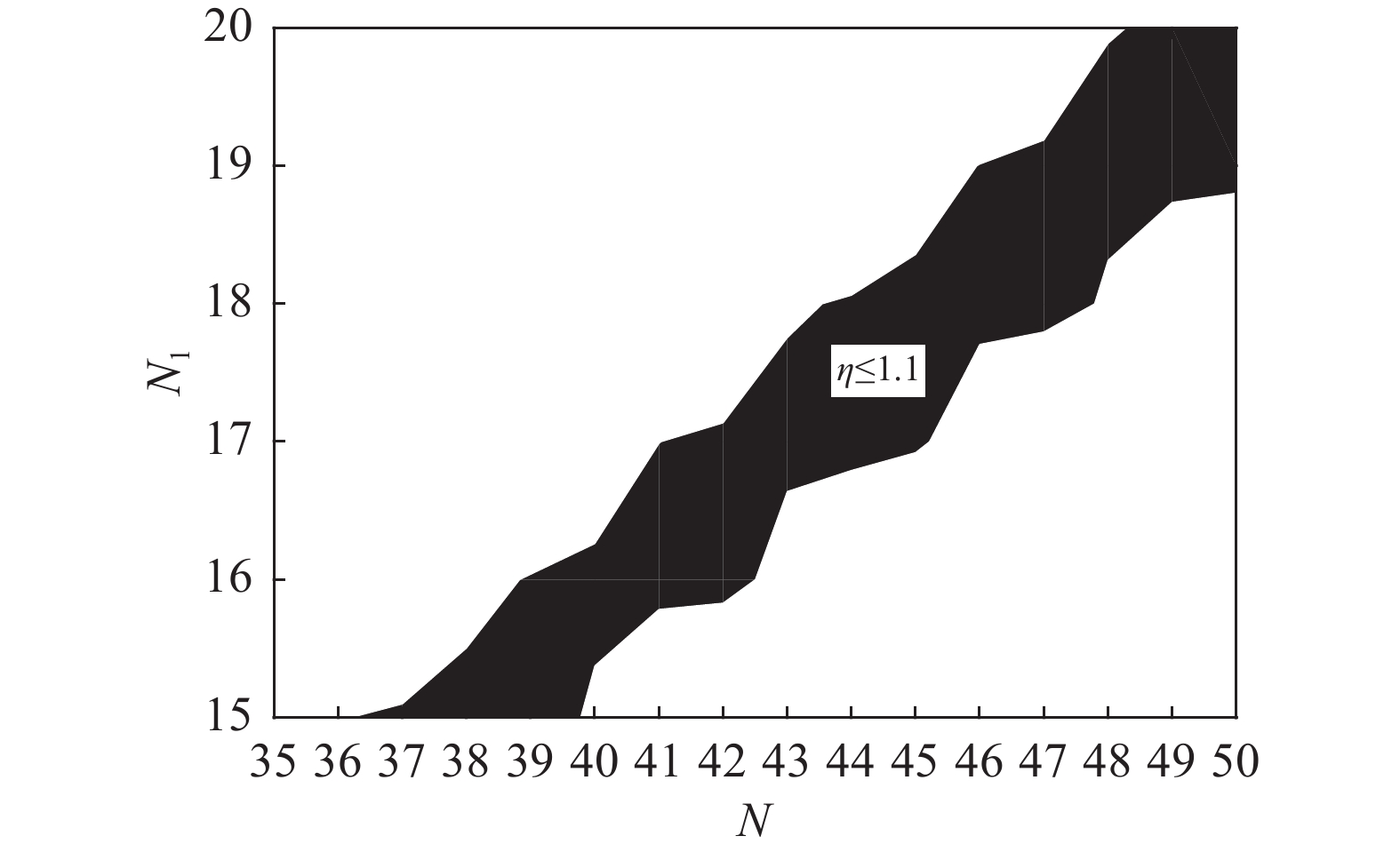
$$ \left\{ \begin{split} &{a_1} = 0.611\;2a \\ &h = 0.621\;6a \\ &{N_1}I = 0.422\;2NI \\ \end{split} \right. $$ (11) 将式(11)代入式(8)中，计算当η=1.1时，a=1.196 m；且计算当Bmin=250 mT时，NI=346.9 kA，N1I=146.5 kA。因为I≤10 kA，所以N≥35，N1≥15，绘制磁场均匀度关于N、N1的分布，如图7所示，其中黑色区域的磁场均匀度在1.1范围内。
Figure 7. Magnetic field uniformity with respect to N and N1 for Helmholtz
从图7中可以看出，当N=38，N1=16时，匝数值最小。此时磁场均匀度η=1.1，Bmin=250 mT时的输入电流I=9.33 kA。
与Helmholtz结构类似，同样对Maxwell线圈进行进一步优化，得出磁感应强度最值与磁场均匀度关于变量参数的关系如下：
$$ \left\{ {\begin{array}{*{20}{l}} {{B_{{\rm{max}}}} = {f_1}\left( {a,{a_1},h,NI,{N_1}I} \right)} \\ {{B_{{\rm{min}}}} = {f_2}\left( {a,{a_1},h,NI,{N_1}I} \right)} \\ {\eta = f\left( {a,{a_1},h,{N \mathord{\left/ {\vphantom {N {{N_1}}}} \right. } {{N_1}}}} \right)} \end{array}} \right. $$ (12) 优化的目的是使得在η=1.1的情况下，线圈结构尺寸最小。由于变量较多，很难直接求解，本文可以选择坐标轮换法对参数进行优化。
坐标轮换法每次只搜索一个变量，可将多维问题转化为一维问题，基本思路如下：
1）选择初始点X0=[x10, x20,
$\cdots $ , xn0]，选择迭代方向e1=[1, 0,$ \cdots $ , 0]T，e2=[0, 1,$ \cdots $ , 0]T，$ \cdots $ ，en=[0, 0,$ \cdots $ , 1]T。2）选择迭代公式
$$ {\boldsymbol{X}}_i^k = {\boldsymbol{X}}_{i - 1}^k + \alpha _i^k{{\boldsymbol{e}}_i} $$ (13) 式中：
K——迭代序号。
3）判断公式
$$ \left| {{\boldsymbol{X}}_n^k{\text{ - }}{\boldsymbol{X}}_0^k} \right| \leqslant \varepsilon $$ (14) 式中：
$\varepsilon $ ——精度。若满足式(14)的要求，停止迭代，输出最优解；若不满足，返回继续求解直至收敛为止。
本文设计的线圈，由于a决定中间最大线圈的尺寸，属于优先级最高的优化对象；a1决定外侧两线圈的尺寸，属于次优先级的优化对象；h决定线圈的轴向尺寸，属于次次优先级的优化对象。
在η=1.1的情况下，先对a进行坐标轮换法求得其最小值；此时a1、h、N/N1的解可能是一组也可能是多组，所以继续以a1为对象进行坐标轮换法求得其最小值；同样h、N/N1的解未定，继续以h为对象进行坐标轮换法求得其最小值；最后求得安匝比N/N1，其中精度选择
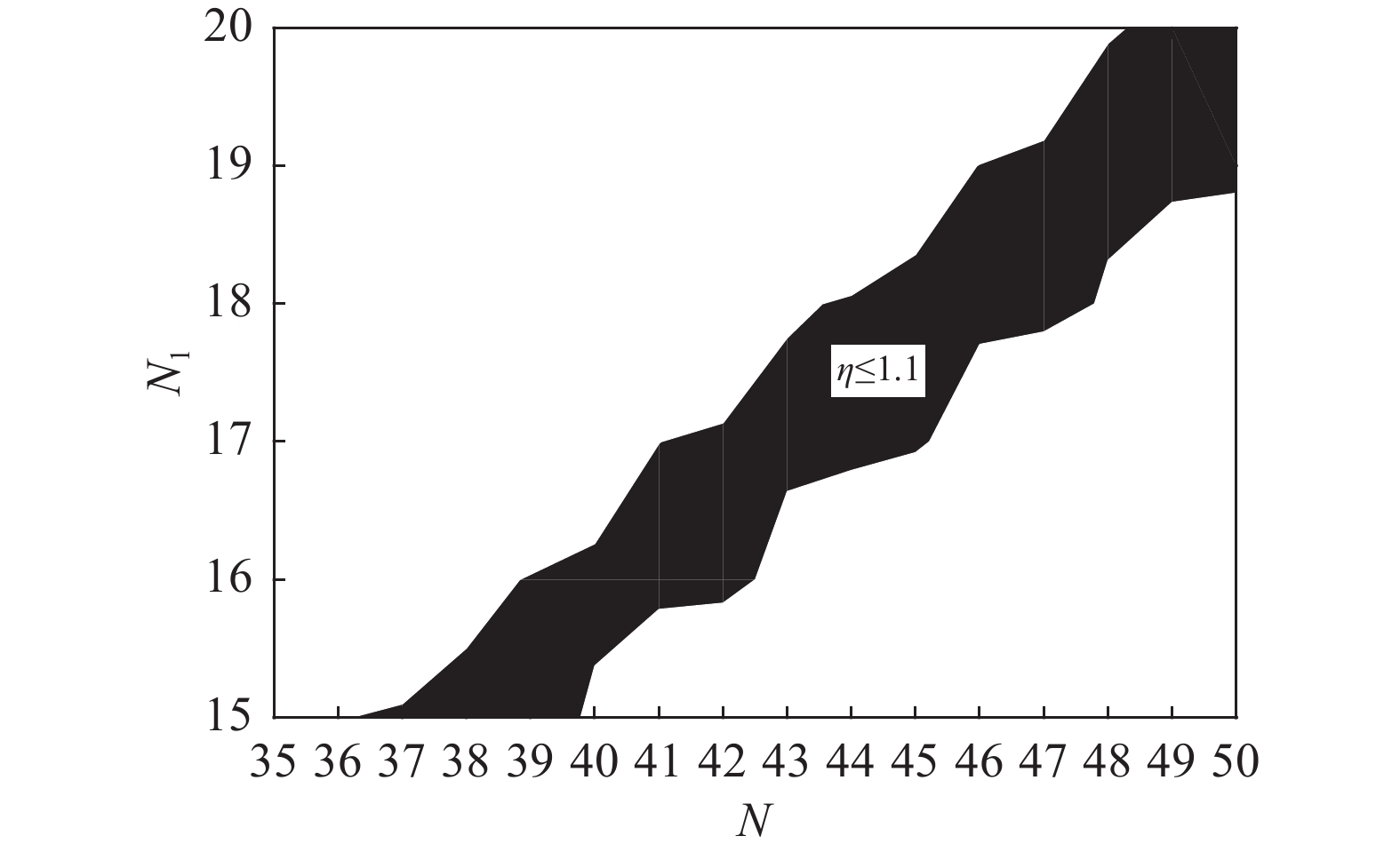
$\varepsilon {\text{ = }}0.001$ 。通过上述计算得到a=1.165 m，a1=0.738 m，h=0.718 m，N/N1=0.4。代入式(12)，计算当Bmin=250 mT时，NI=340.1 kA，N1I=136.1 kA，所以N≥35，N1≥14，绘制磁场均匀度关于N、N1的分布，如图8所示。
Figure 8. Magnetic field uniformity with respect to N and N1 for Maxwell
从图8中可以看出，当N=37，N1=15时，匝数值最小。此时磁场均匀度η=1.1，Bmin=250 mT时的输入电流I=9.32 kA。
从表2可以看出，优化结构的体积更小，输入电流相同的情况下匝数更少，成本更低。
参数 Maxwell结构 优化结构 η 1.1 1.1 Bmin/mT 250 250 a/m 1.196 1.165 a1/m 0.731 0.738 h/m 0.743 0.718 I/kA 9.33 9.35 N 16:38:16 15:37:15 Table 2. Distribution of axial magnetic field parameter comparison between Maxwell and Maxwell optimized structure
对比表1和表2可知，Maxwell优化结构线圈相对于其他结构而言，体积最小，输入电流更小，并且匝数更少，所以本文设计选择此结构作为最终结构。
-
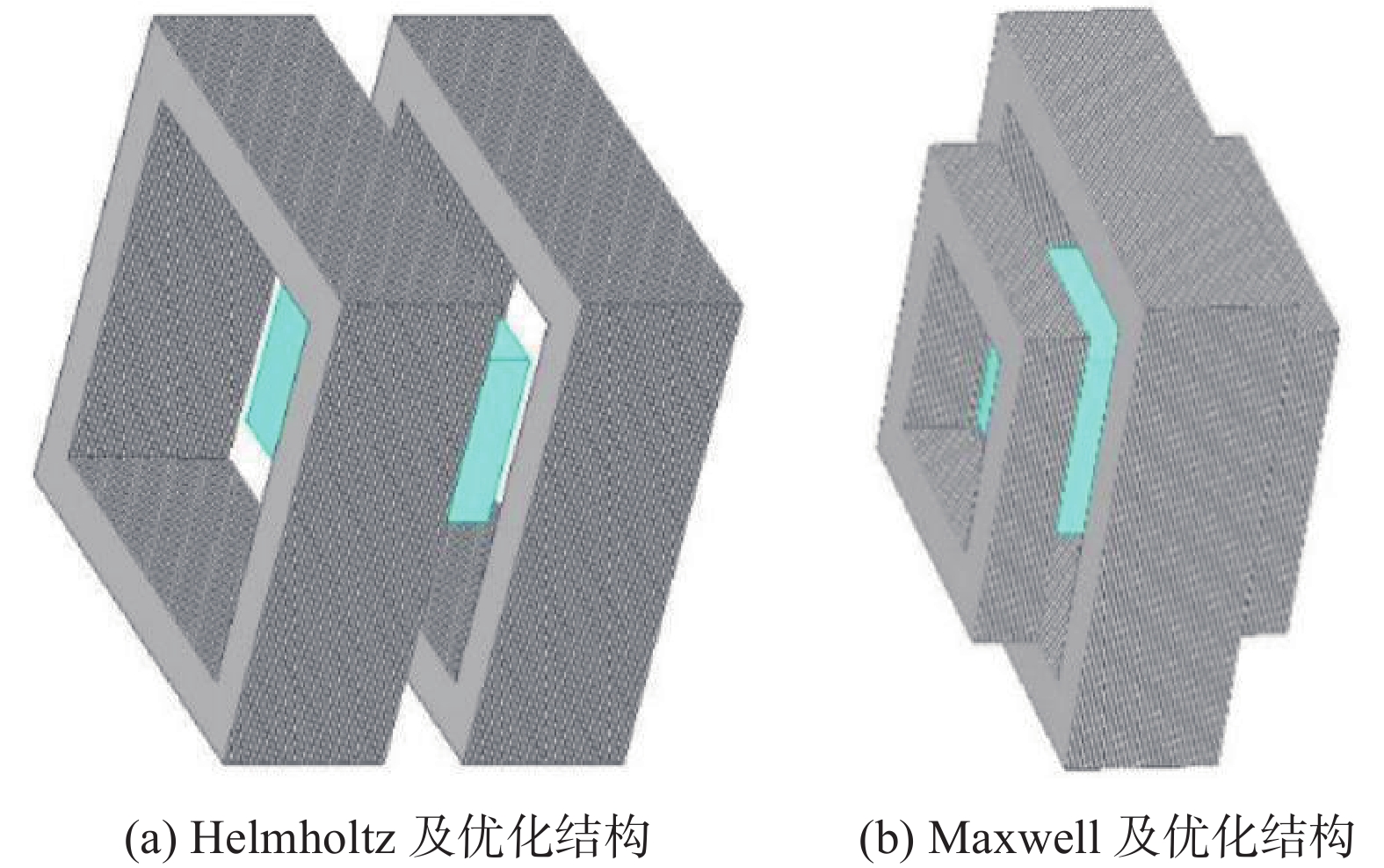
线圈采用铝排结构，实际系统使用自然风冷进行散热，在热负荷的考虑上不能过高，实际演算后取电流密度1.56 A/mm2，导体截面取(10 kA)/(1.56 A/mm2)=6 410.3 mm2；而线圈匝数很多，为了保证轴向长度不至于过长，同时考虑到导体强度，取轴向长度为20 mm，另一边长为(6 410.3 mm2)/(20 mm)≈320 mm；导体间距在考虑绝缘安全，取3 mm即可。建立有限元模型，如图9所示。
Figure 9. Finite element model of coil
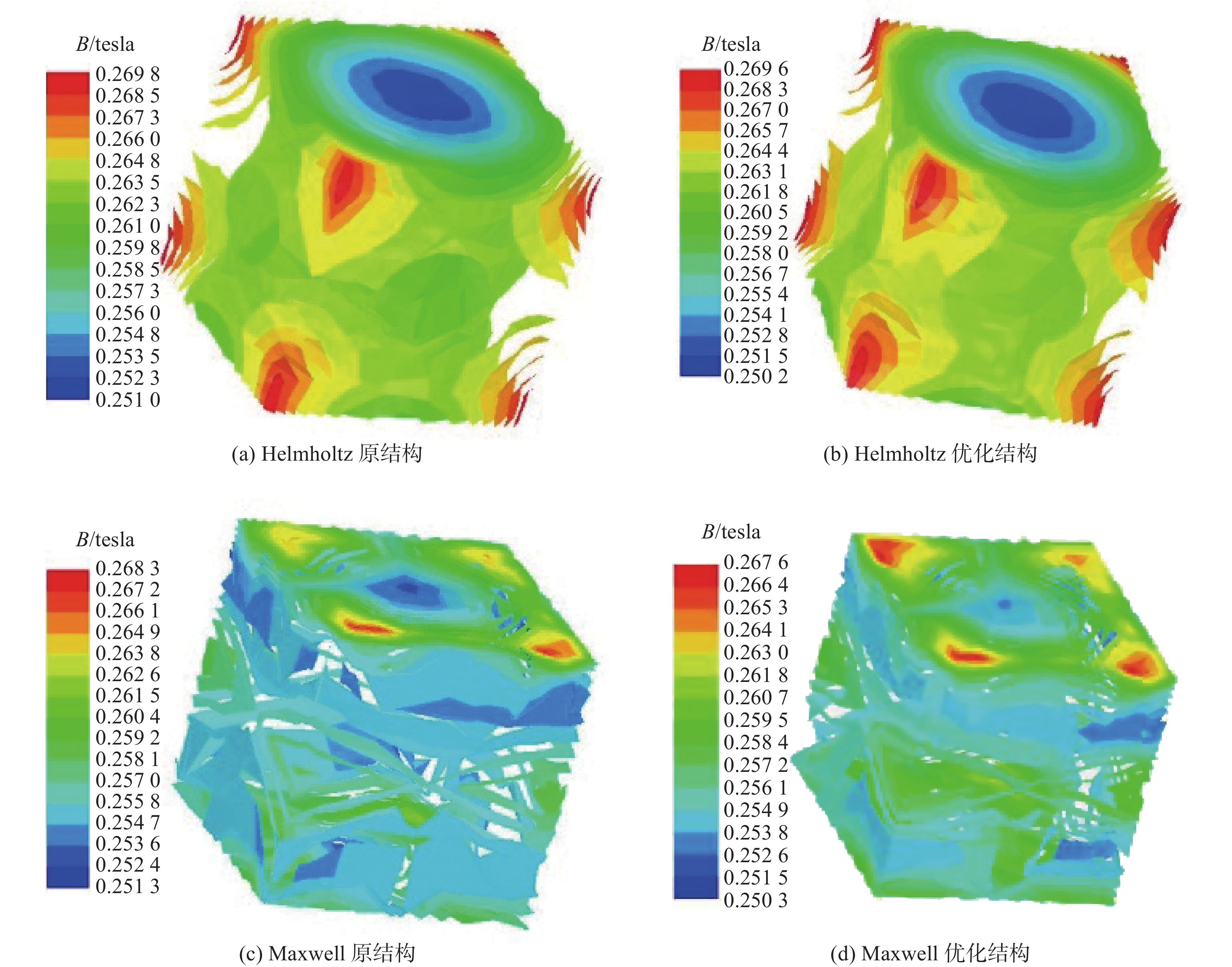
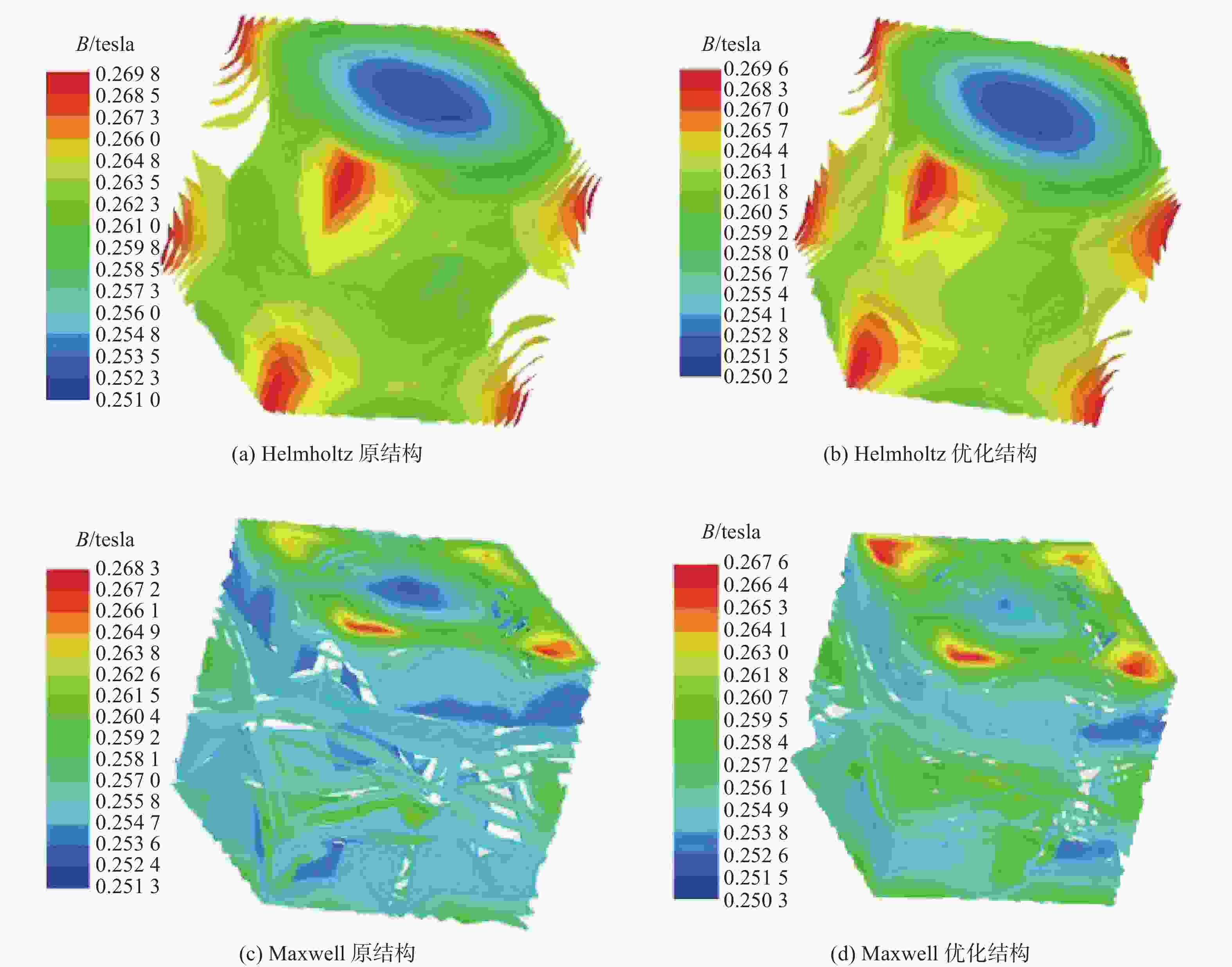
仿真计算中心1 m×1 m×1 m区域的轴向磁场分布，如图10所示。
Figure 10. Distribution of axial magnetic field
仿真结果与解析计算进行对比，如表3所示。可以看出，仿真结果相对于解析计算，均匀度更好，主要是因为每匝线圈在轴向均匀分布，对于磁场均匀度有一定的改善作用，但是在达到Bmin=250 mT的条件下，所需要的电流相应地有所增加。整体而言，误差在可接受范围内，设计方案效果良好。
结构 方法 η Bmin/mT Bmax/mT I/kA Helmholtz
原结构解析法 1.100 250.0 275.0 9.93 有限元法 1.075 251.0 269.8 10.10 误差 2.28% 0.40% 1.89% 1.71% Helmholtz
优化结构解析法 1.100 250.0 275.0 9.76 有限元法 1.078 250.2 269.6 9.95 误差 2.04% 0.08% 1.96% 1.95% Maxwell
原结构解析法 1.100 250.0 275.0 9.33 有限元法 1.068 251.3 268.3 9.57 误差 2.94% 0.52% 2.44% 2.52% Maxwell
优化结构解析法 1.100 250.0 275.0 9.35 有限元法 1.069 250.3 267.6 9.59 误差 2.81% 0.12% 2.69% 2.57% Table 3. Comparison between analytical method and structural parameter optimization method
-
Helmholtz和Maxwell线圈结构在产生均匀磁场方面具有极大优势，本文针对1 m3立方体空间磁场均匀度不大于1.1的要求采用这两种结构来分析。首先对Helmholtz线圈及其优化结构分析，绘制出磁场均匀度关于尺寸的分布，求得计算的一般通用公式。然后使用泰勒展开求解Maxwell线圈的尺寸关系并求解相应的尺寸值，再利用坐标轮换法对线圈结构进行优化。对比分析各项结果，在满足条件的情况下，从尺寸最小，匝数最少方面，选择Maxwell线圈优化结构作为最优设计方案。由此也可以看出当线圈组数越多，磁场均匀性就会越好，但是考虑到更多线圈组数的制造安装难度，不考虑更复杂的结构。文章最后通过有限元仿真，验证了结果的正确性。
Optimization of High Uniformity Steady-State Magnetic Field Generator
doi: 10.16516/j.gedi.issn2095-8676.2022.02.011
- Received Date: 2022-04-28
- Rev Recd Date: 2022-06-06
- Available Online: 2022-06-24
- Publish Date: 2022-06-25
-
Key words:
- immunity test /
- induction coil /
- solenoid /
- magnetic field measurement /
- finite element method /
- magnetic field uniformity
Abstract:
| Citation: | HE Yan. Optimization of High Uniformity Steady-State Magnetic Field Generator[J]. SOUTHERN ENERGY CONSTRUCTION, 2022, 9(2): 82-89. doi: 10.16516/j.gedi.issn2095-8676.2022.02.011
|
DownLoad:
