-
在以新能源为主体的新型电力系统中,高比例可再生能源的峰谷差大、波动性强等特征将更加凸显,电网的稳定运行将受到巨大考验。储能技术将在提高电网对新能源的消纳能力,削峰填谷,提高电能质量等方面发挥重要作用。
已投入商业应用的大规模储能技术主要有抽水蓄能和压缩空气储能[1]。抽水蓄能是目前最为经济可靠,容量最大,寿命最长的大规模储能技术,面临的主要挑战在于其建设对地理条件要求比较高,靠近负荷中心的建设场地越来越难以寻找[2]。压缩空气储能通常采用地下盐穴储存高压空气,储气规模大,建造成本与抽水蓄能相当,但同样依赖于地理条件。为此,有学者提出将人工造穴[3]、金属材料高压容器[4]、柔性复合材料高压容器[5]等作为储气装置,以期摆脱地理条件的限制[6]。
液化空气储能在压缩空气储能的基础上增加液化环节,将空气以低压液态储存在绝热储罐中。由于液空的密度远大于压缩空气的密度,需要的储存空间大幅减少。液化空气储能不依赖于盐穴等地理条件,建设周期短,使用寿命超过20年[7]。然而由于液化过程存在不可逆损失,液化空气储能的循环效率比压缩空气储能低5%~10%。考虑到压缩空气储能和液化空气储能的优势与局限性,两者可以互为补充[8]。
1977年,Smith[9]首次提出使用液化空气作为储能介质给电网调峰,目的是开发一个比传统压缩空气储能系统体积更小的电能存储系统。液化空气储能的概念提出后,国内外研究人员致力于推动其商业化。Kishimoto等[10]建造了一个2.6 MW的由液化空气驱动的朗肯循环,证实了其具有良好的发电稳定性。Chino等[11]设计了一个带补燃和LNG冷能利用的液化空气储能方案。Highview Power和英国利兹大学的合资企业设计和建造了世界上第一座集成的液化空气储能电厂[12]。这座350 kW/2.5 MWh的中试规模的电厂于2010年投入使用,于2013年完成测试,之后被转移到伯明翰大学进行进一步的研究和开发。该系统为液化空气储能的商业化发展奠定了基础。2018年,Highview Power公司的另一座5 MW/15 MWh的预商用电厂投入运营[13],该项目的设计效率为55%。近期,Highview Power公司在英国和美国部署了两座50 MW的液化空气储能电厂[14],取名为CRYOBattery(低温电池)。这将是全球第一批并网连接的液化空气储能电厂。
截至目前,国内液化空气储能示范项目仅有一个,是国家电网在苏州市同里镇建设的综合能源服务中心内的500 kW液态空气储能示范项目,项目于2018年建成。该液化空气储能系统可为园区提供500 kWh电力,同时,利用溴化锂冷热双效机组为园区供冷和供热。
液化空气储能循环主要由液化循环加动力循环组成。液化循环将常温常压的空气液化得到液空,液空经过动力循环的加压汽化后膨胀做功最终变成常温常压下的空气。在液化循环方面,不同研究人员采用了不同的技术路线,如林德循环[15]、克劳特循环[16]、卡皮查循环[17]和海兰德循环[18]。但在发电循环方面,朗肯循环几乎是唯一选择[16-18]。在液化循环和发电循环的基础上,通常还辅以储冷储热系统以实现对冷能和热能的回收利用[19-21]。
总体来看,液化空气储能的工业化应用处于初级阶段,设计方法尚不成熟。厘清液化空气储能系统液化率和循环效率的关键影响因素及其作用机制,探索适用于提高循环效率的方法,对于该技术的发展是非常必要的。文章对液化空气储能系统基本循环进行热力学分析,探究冷能回收和热能回收的必要性;分析关键参数如冷能回收终点温度、高压压力、释能压力的影响机制,为高效的液化空气储能系统的参数设计提供参考。
-
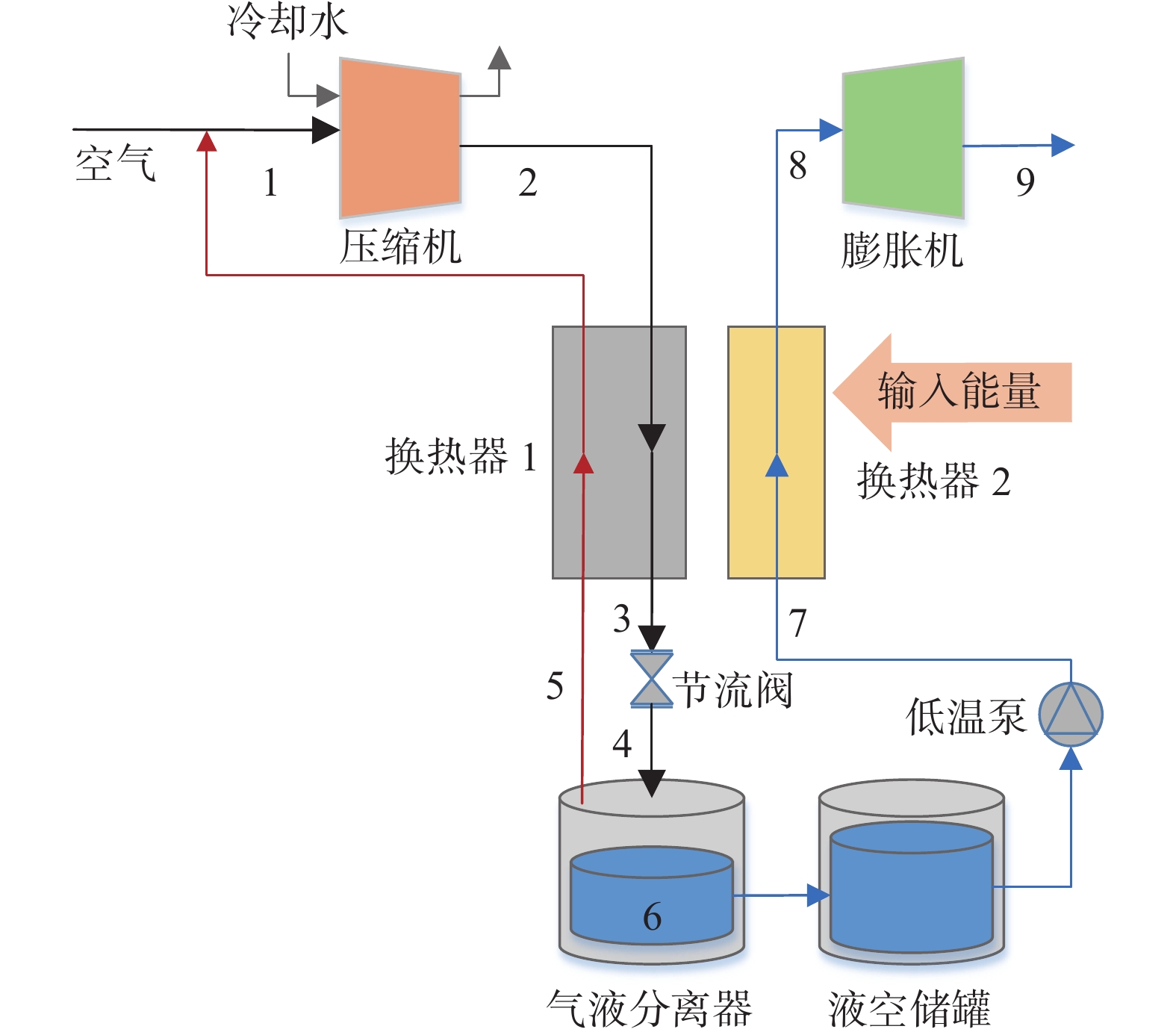
文章中液化空气储能基本循环由最简单的液化循环(林德循环)以及基础的动力循环(朗肯循环)组成。根据液化循环与动力循环的能量耦合程度分为三类:分离式循环、冷能回收循环、冷能热能回收循环。在分离式循环中,液化循环与动力循环相互独立;在冷能回收循环中,动力循环液空汽化复温过程的冷量被回收用于液化循环部分的空气预冷;冷能热能回收循环在此基础上,进一步回收液化循环压缩热用于动力循环的液空复温。
为了抓住主要矛盾,文章进行热力学分析时做出如下假设:除节流阀之外没有不可逆压降;无漏热;换热器效率、压缩机、低温泵、膨胀机的效率均为100%。
-
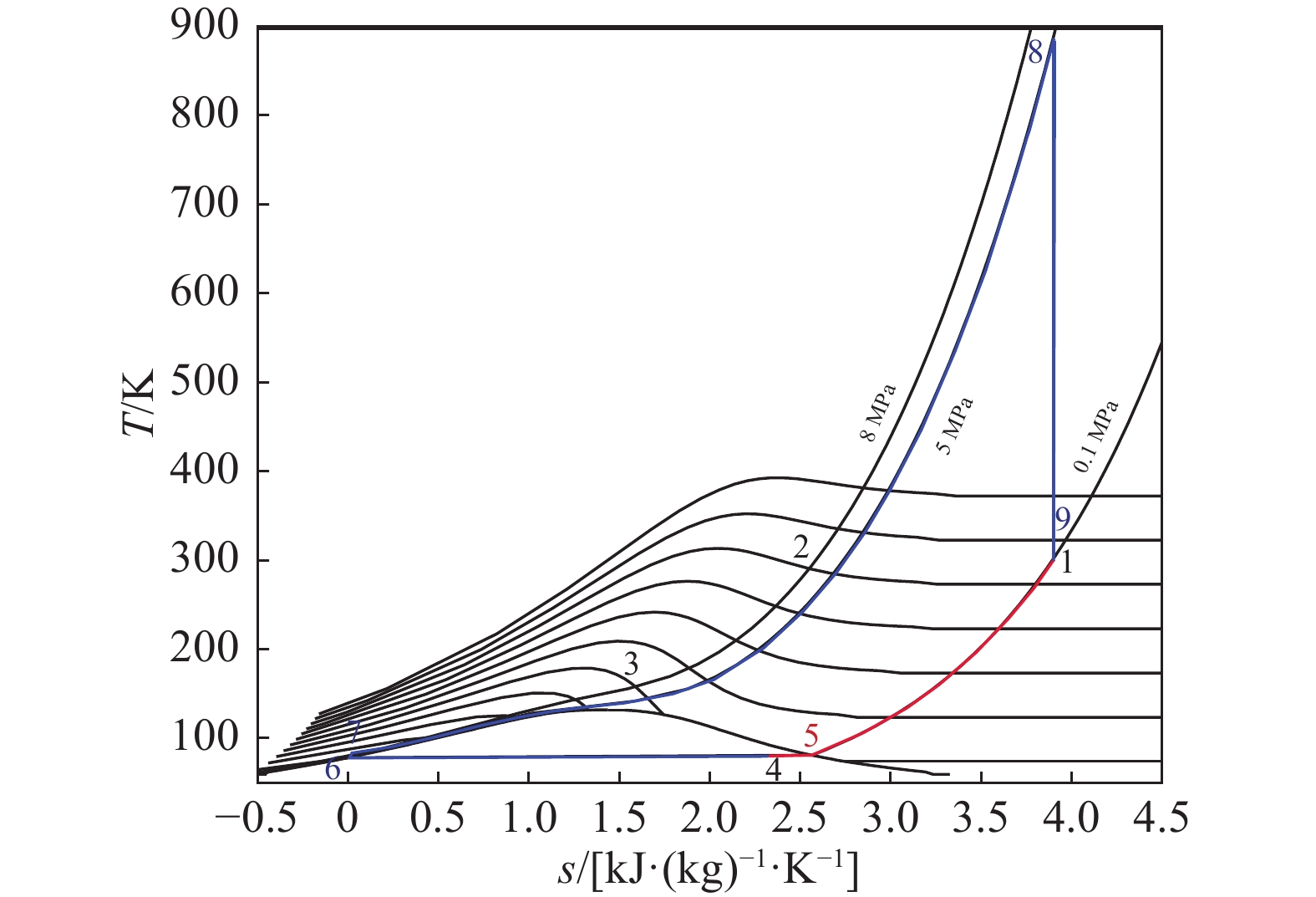
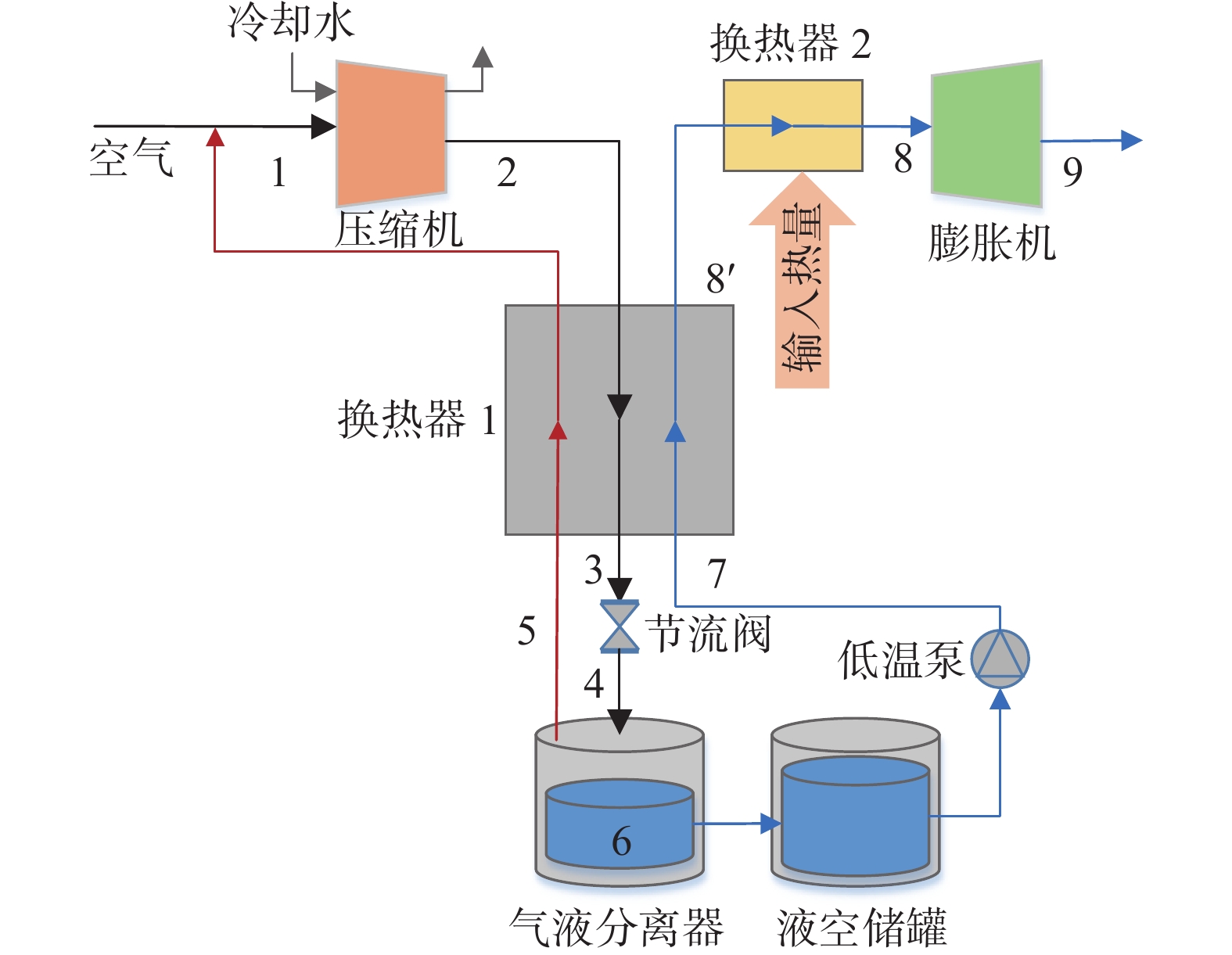
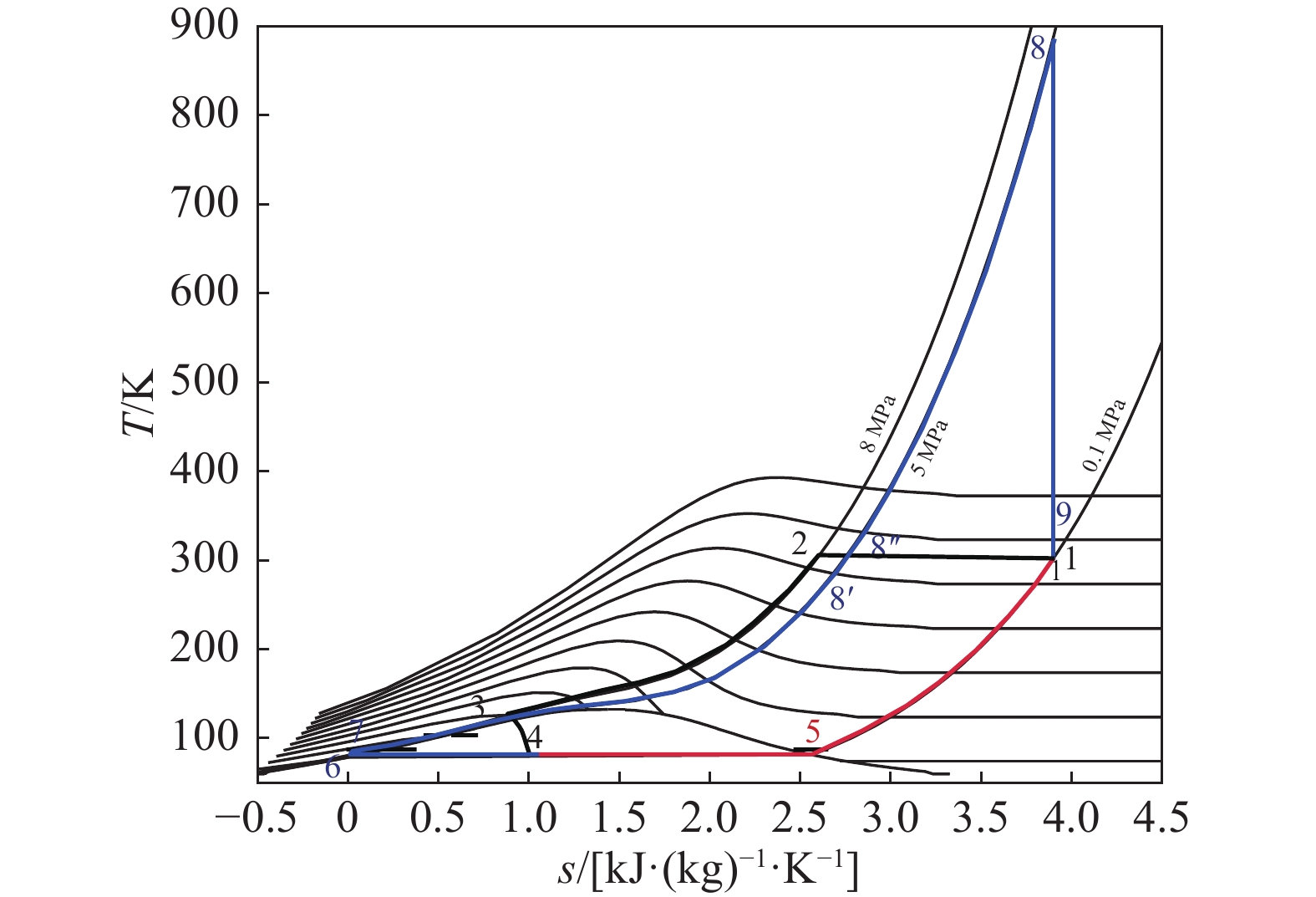
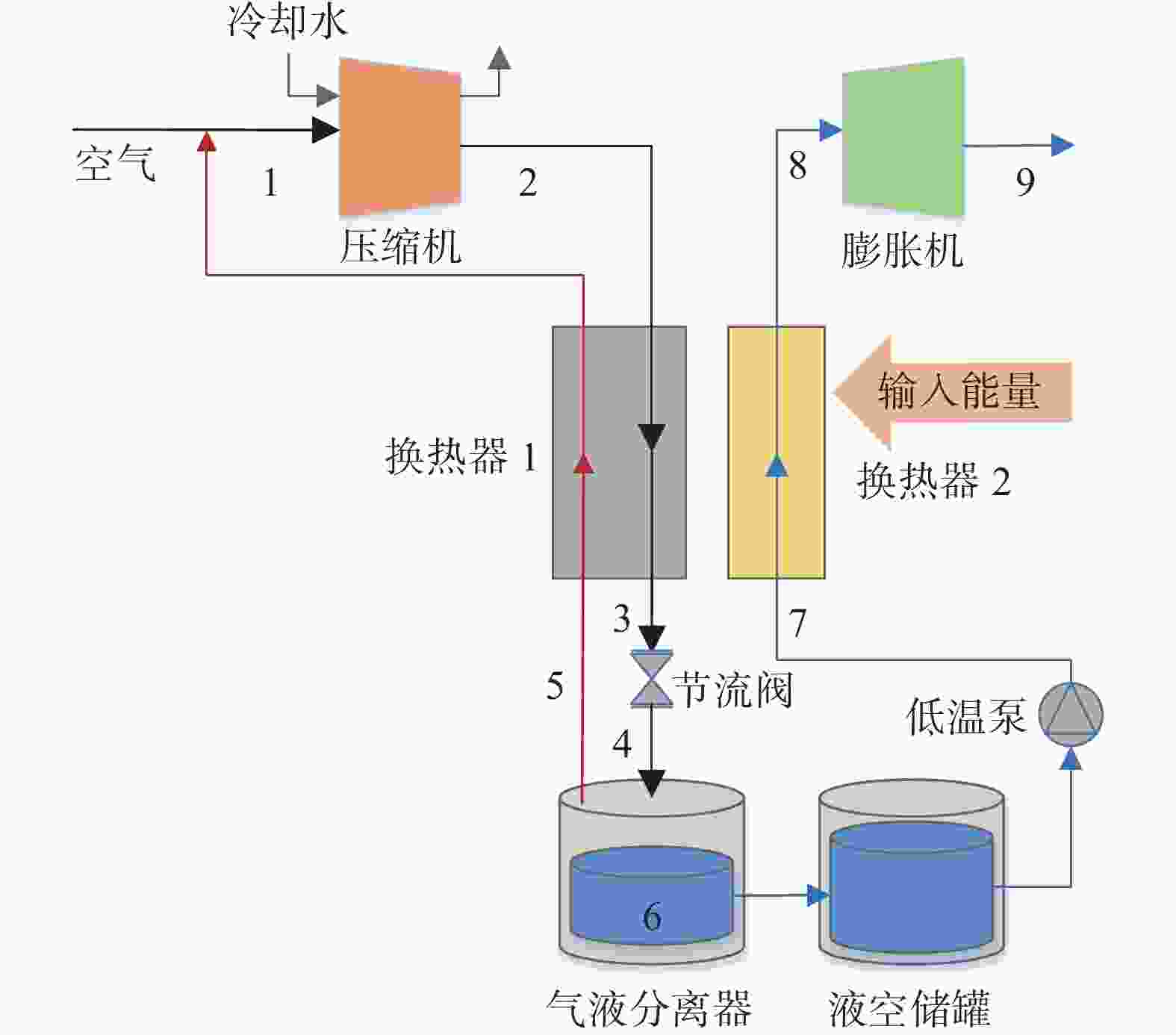
分离式循环示意图如图1所示,温-熵(T-s)图如图2所示。其中林德液化循环由等温压缩(1-2)、等压冷却(2-3)、等焓节流(3-4)、气液分离(4-6-5)、低温气体等压复温(5-1)组成。朗肯动力循环由液空等熵增压(6-7)、等压复温(7-8)、等熵膨胀(8-9)组成。
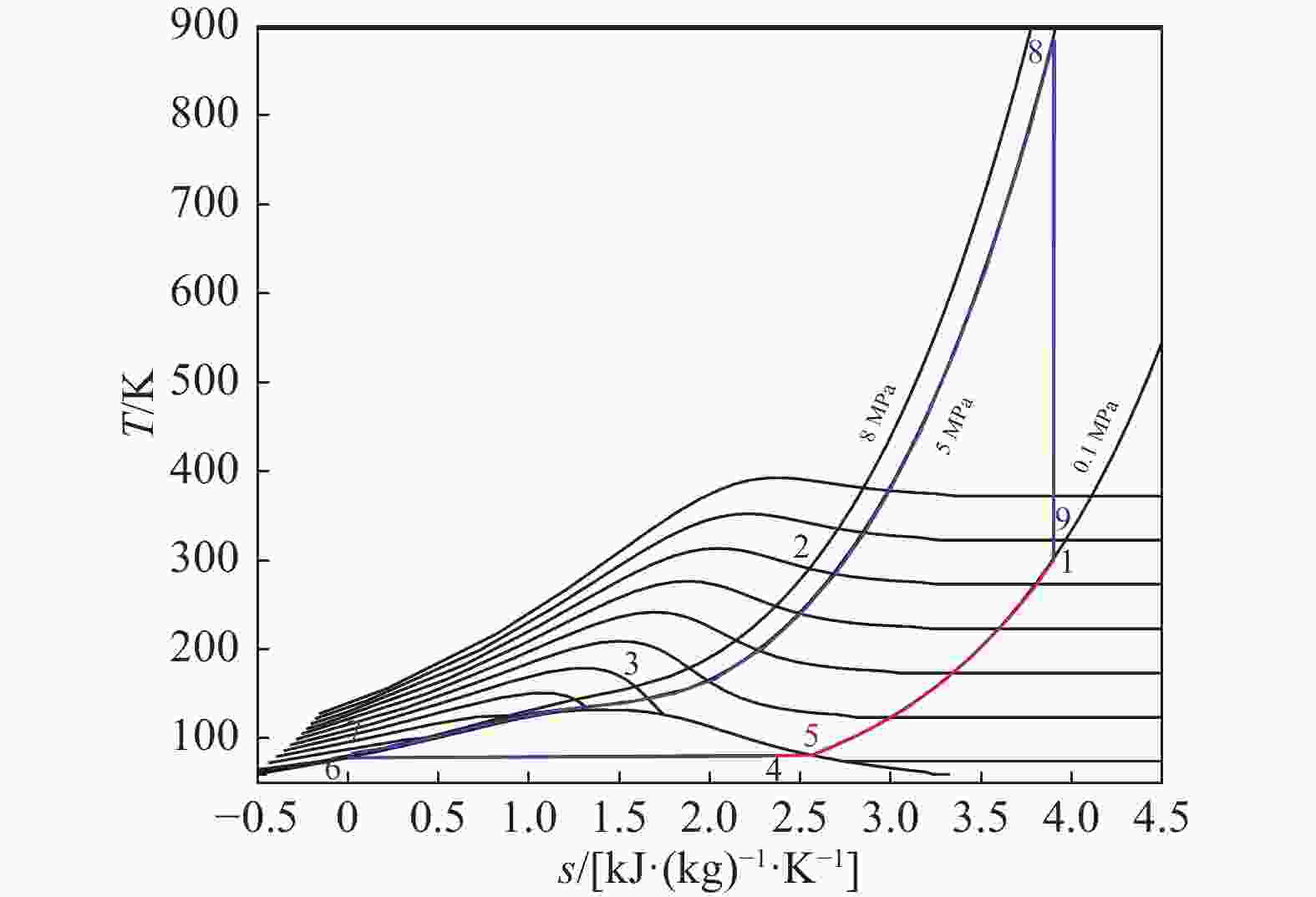
Figure 2. T-s diagram of the separate cycle (data shown in Tab. 1)
等温压缩(1-2)过程中压缩机电功耗和放热量分别为:
$$ {w_{\text{c}}} = {T_1}({s_1} - {s_2}) - ({h_1} - {h_2}) $$ (1) $$ {q_{\text{c}}} = {T_1}({s_1} - {s_2}) $$ (2) 式中:
wc ——单位质量空气的压缩电功耗(kJ/kg);
T ——温度(K);
s ——空气的比熵[kJ/(kg·K)];
h ——空气的比焓(kJ/kg);
qc ——单位质量空气的压缩放热量(kJ/kg);
1,2——下标数字表示状态点序号。
高压空气经过节流阀节流膨胀至点4,此时有部分气体被液化,节流后未液化气体从气液分离器引出(点5),流经换热器1复温到常温返回到压缩机入口。对换热器1、节流阀和气液分离器做质量和能量平衡,得液化率y为:
$$ y = \dfrac{{{h_1} - {h_2}}}{{{h_1} - {h_6}}} $$ (3) 式中:
y ——液化率。
由于液空的不可压缩性,在等熵增压(6-7)过程中低温泵电功耗为:
$$ {w_{\text{p}}} = \dfrac{{{p_{\text{7}}} - {p_{\text{6}}}}}{{{\rho _6}}} $$ (4) 式中:
wp ——单位质量液空的泵功(kJ/kg);
p ——液空压力(kPa);
ρ ——液空密度(kg/m3)。
增压后的液空流经换热器2汽化升温(7-8),此过程单位质量液空的吸热量为:
$$ {q_{{\text{in}}}} = {h_{\text{8}}} - {h_{\text{7}}} $$ (5) 式中:
qin ——单位质量液空复温过程从外界吸热量(kJ/kg)。
高温高压的空气膨胀做功(8-9)带动发电机对外发电实现释能,单位质量空气的做功量为:
$$ {w_{\text{t}}} = {h_{\text{8}}} - {h_{\text{9}}} $$ (6) 式中:
wt ——单位质量空气做功量(kJ/kg)。
储能循环效率定义为释能输出的功与输入的功和热的比值:
$$ \eta = \dfrac{{y({w_{\text{t}}} - {w_{\text{p}}})}}{{{w_{\text{c}}} + y \cdot {q_{{\text{in}}}}}} = \dfrac{{{w_{\text{t}}} - {w_{\text{p}}}}}{{{{{w_{\text{c}}}} \mathord{\left/ {\vphantom {{{w_{\text{c}}}} y}} \right. } y} + {q_{{\text{in}}}}}} $$ (7) 式中:
η ——循环效率。
对上式进行定性分析可以发现,增加液化率y、降低输入的热量qin都有助于提升循环效率。
-
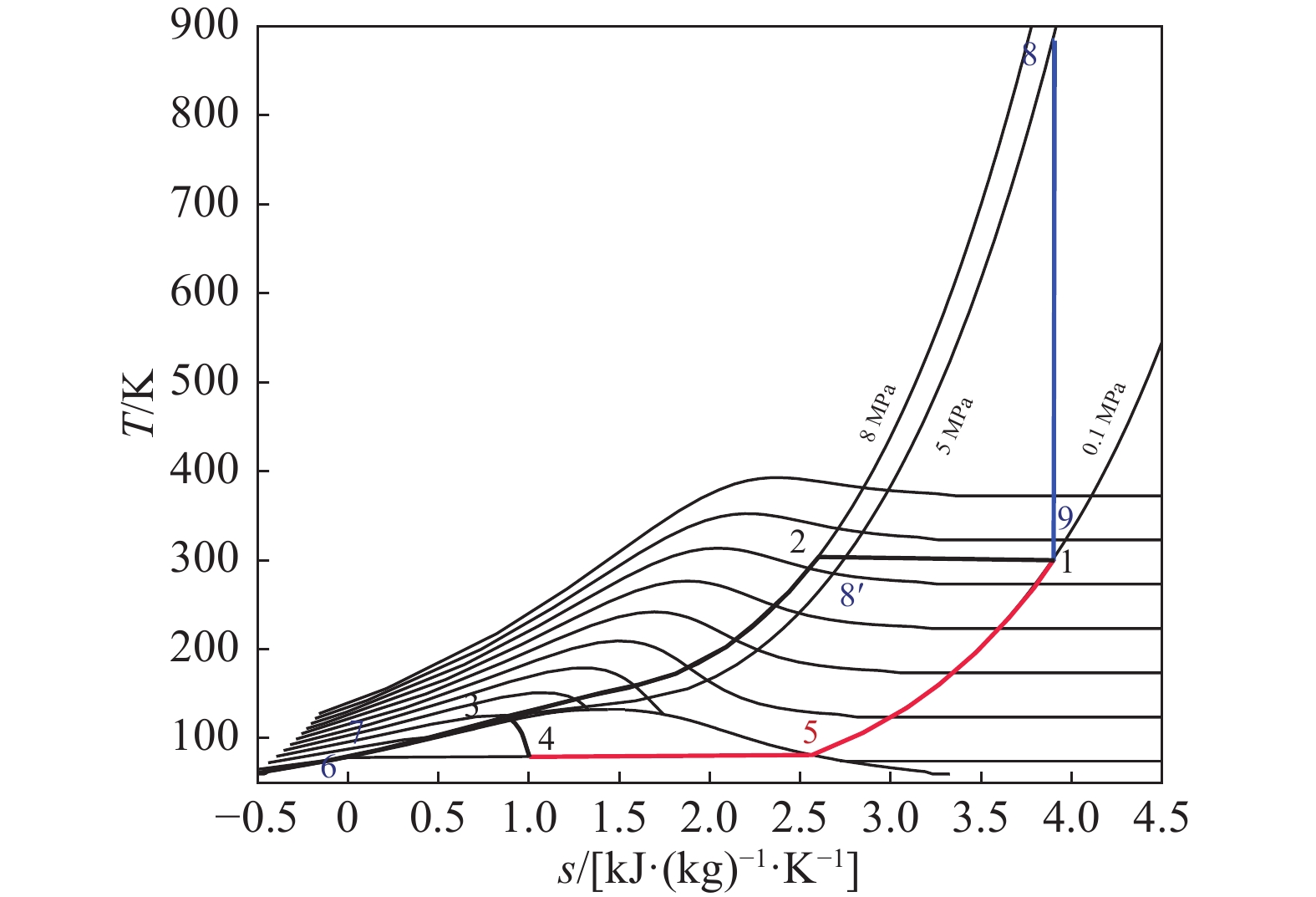
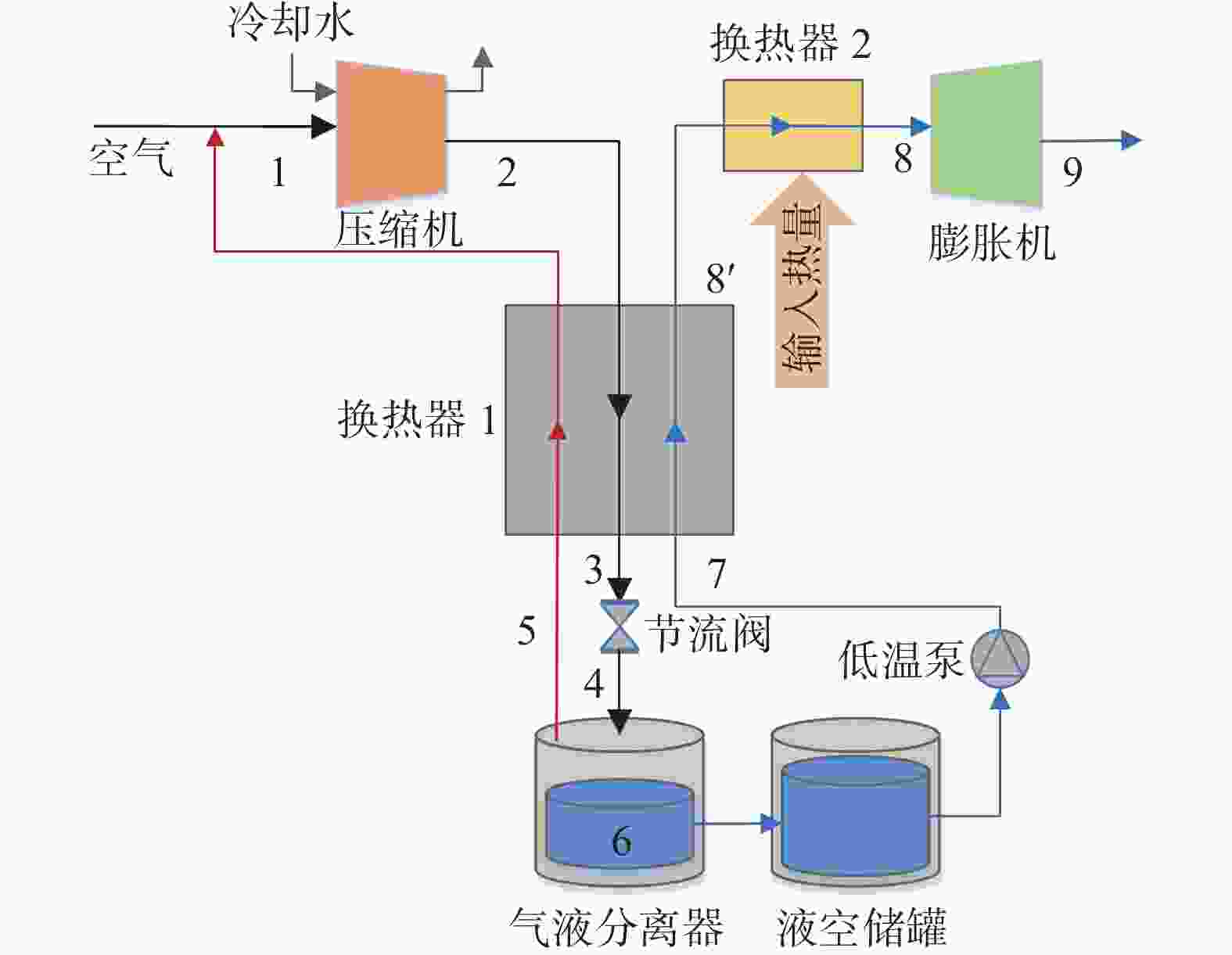
冷能回收循环示意图如图3所示,T-s图如图4所示。在分离式循环的基础上,将液空复温过程中低于室温的部分冷能回收,用于预冷液化循环中的空气,增加了一个状态点8'。
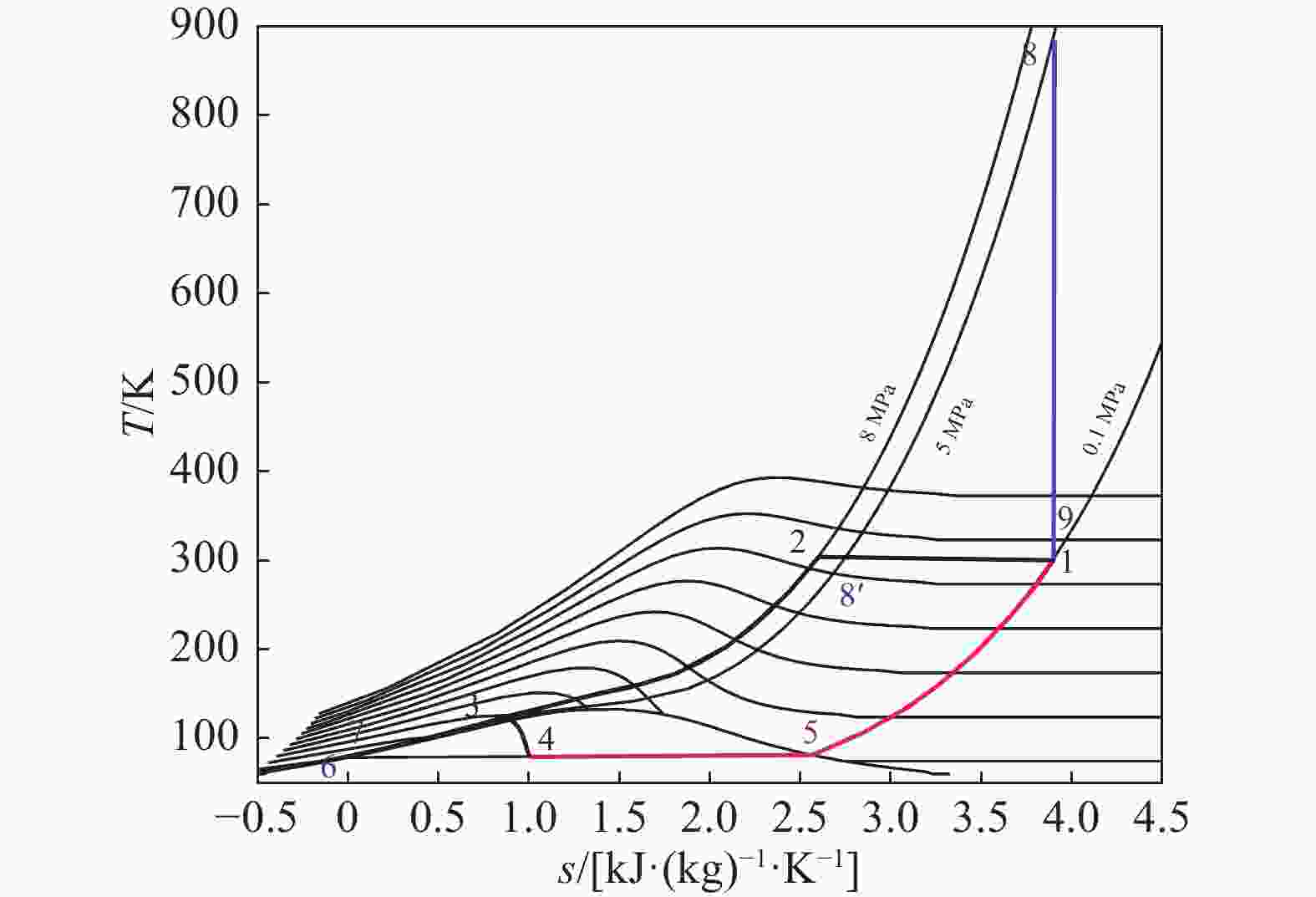
Figure 4. T-s diagram of the cooling capacity recovery cycle (data shown in Tab. 2)
单位质量液空复温过程回收的冷能qrec为:
$$ {q_{{\text{rec}}}} = {h_{{\text{8}'}}} - {h_{\text{7}}} $$ (8) 式中:
qrec ——单位质量液空回收的冷能(kJ/kg)。
复温后的空气流经换热器2升温(8'-8),此过程单位质量液空的吸热量qin减小为:
$$ {q_{{\text{in}}}} = {h_{\text{8}}} - {h_{{\text{8}{\rm{'}}}}} $$ (9) 此时,对换热器1、节流阀和气液分离器做质量和能量平衡,得到新的液化率y为:
$$ y = \frac{{{h_1} - {h_2}}}{{{h_1} - {h_6} - {q_{{\text{rec}}}}}} $$ (10) 冷能回收循环效率同样为式(7)。将式(10)与式(3)比较可以发现冷能回收循环的液化率表达式中分母更小,液化率更大,可以预见循环效率会得到提升。
-
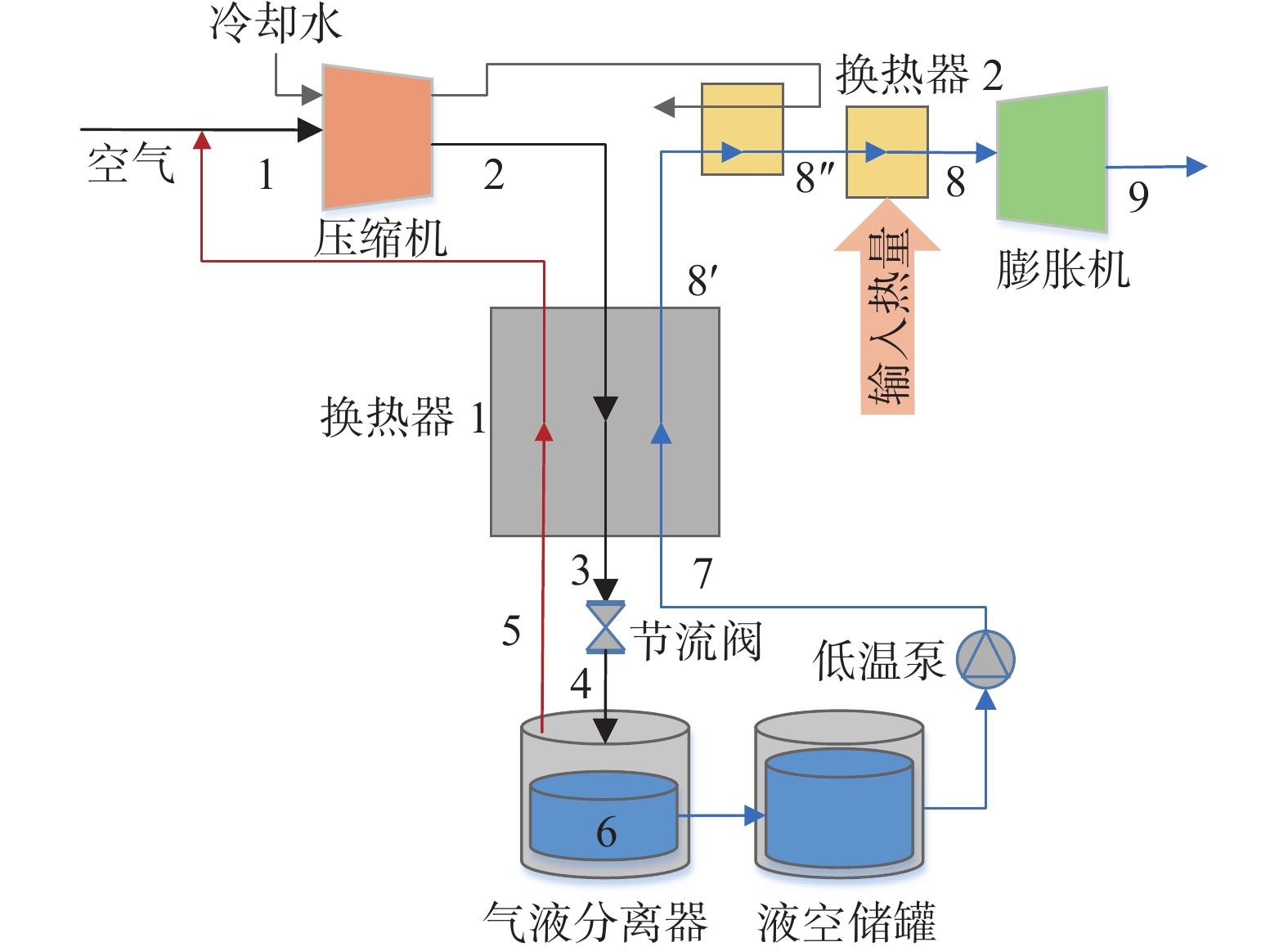
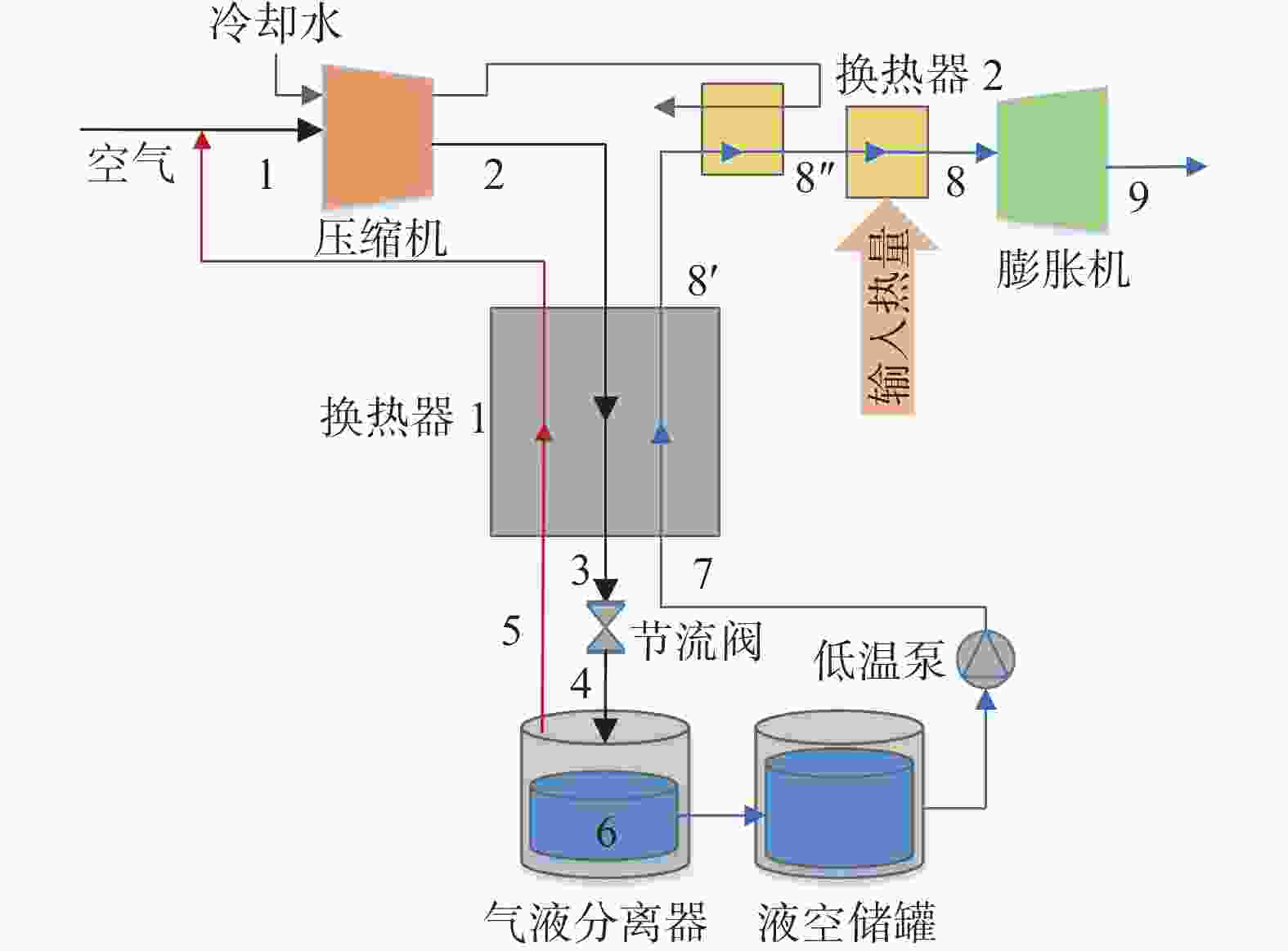
冷能热能回收循环示意图如图5所示,T-s图如图6所示。在冷能回收循环的基础上,将液化循环中空气的压缩热回收,用于辅助动力循环中的空气复温,增加了一个状态点8''
。 单位质量空气复温过程回收利用的压缩热为:
$$ {q}_{\text{rec,h}}={h}_{\text{8}''}-{h}_{\text{8}{\rm{'}}} $$ (11) 式中:
qrec,h ——单位空气复温过程回收利用的压缩热量(kJ/kg)。
复温后的空气流经换热器2升温(8''
-8'),此过程单位质量液空的吸热量qin进一步减小为: $$ {q}_{\text{in}}={h}_{\text{8}}-{h}_{\text{8}''} $$ (12) 此时,液化率y与冷能回收循环一致,为式(10),循环效率同样为式(7)。
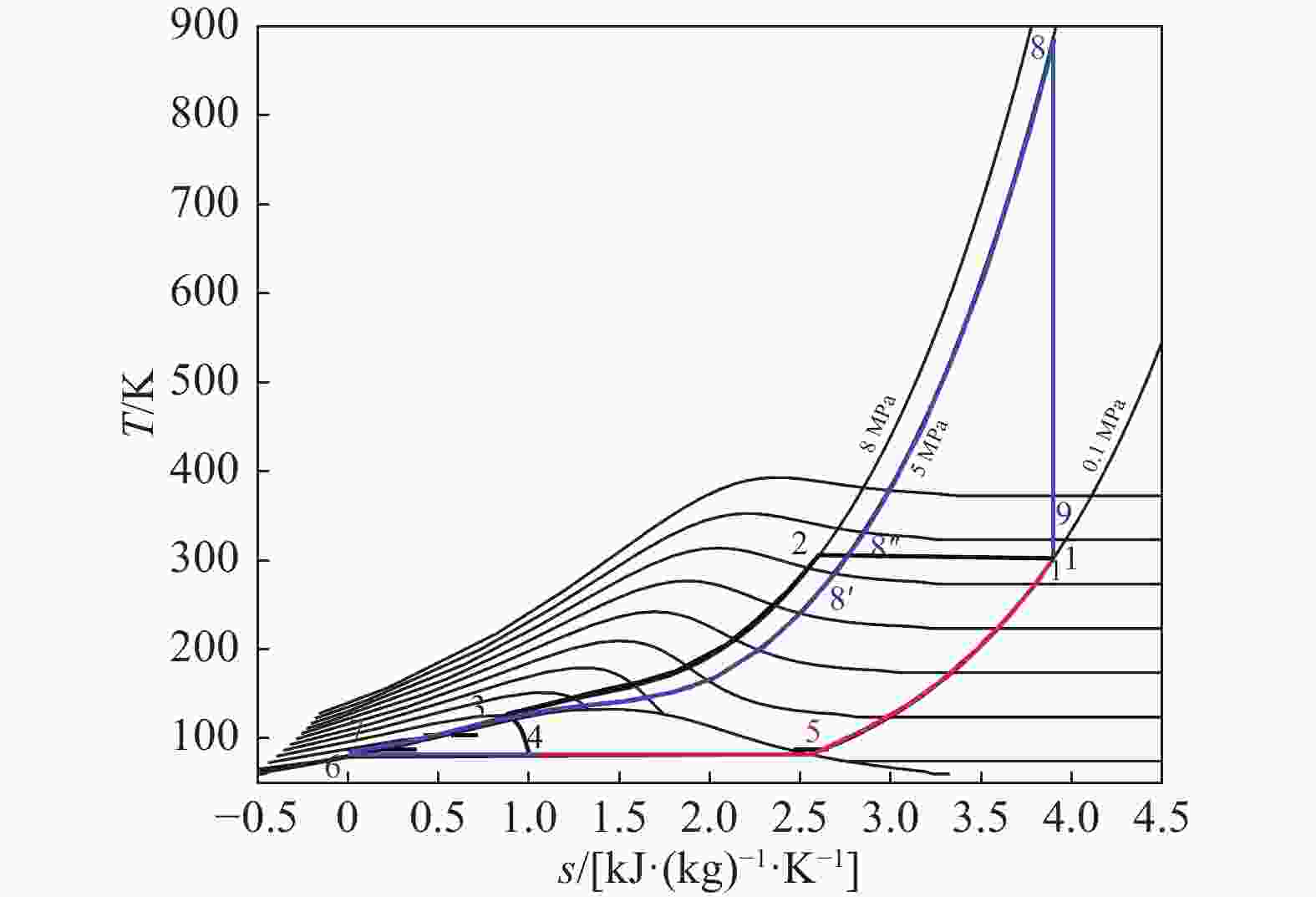
Figure 6. T-s diagram of the cooling capacity and heat recovery cycle (data shown in Tab. 3)
-
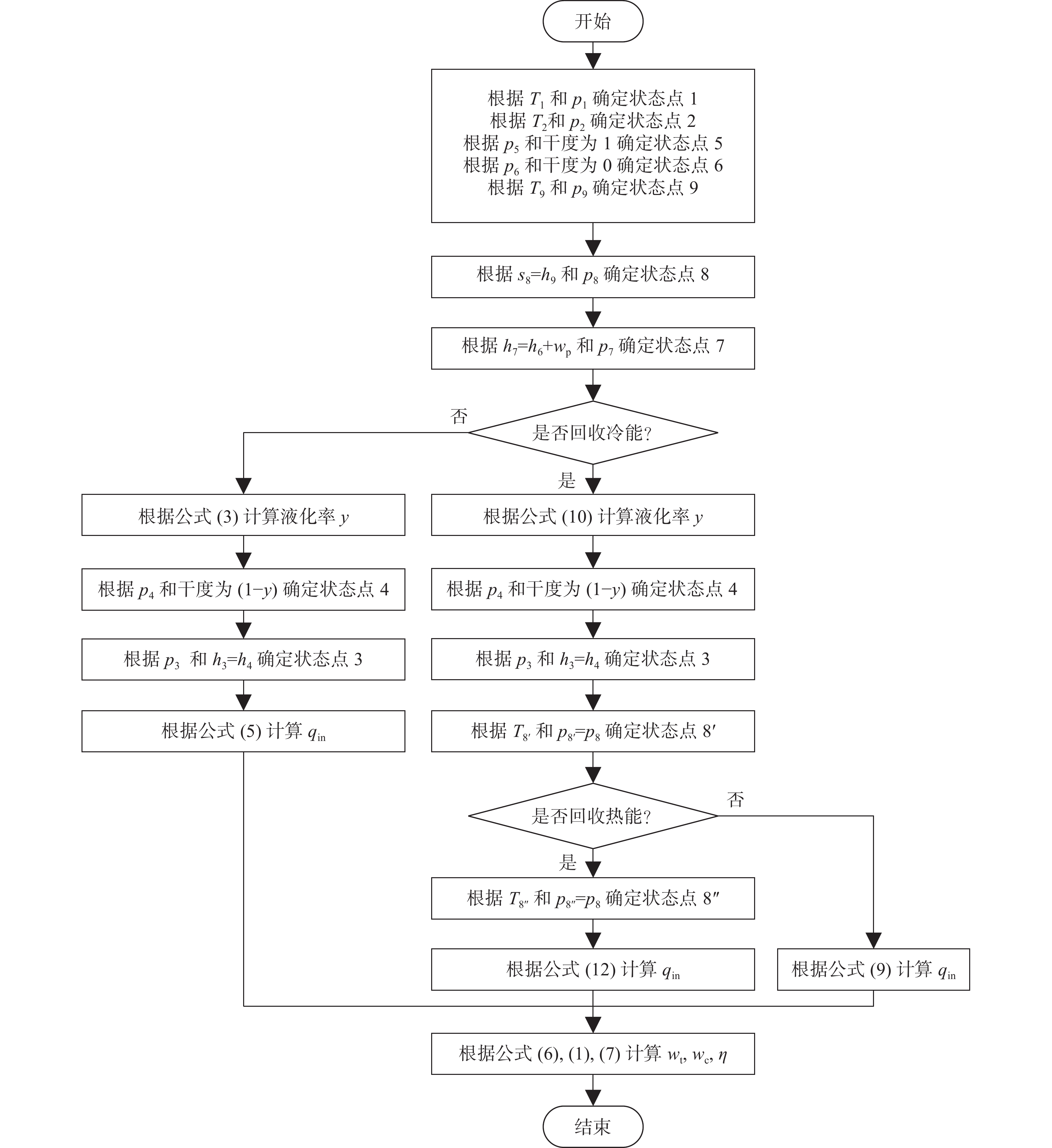
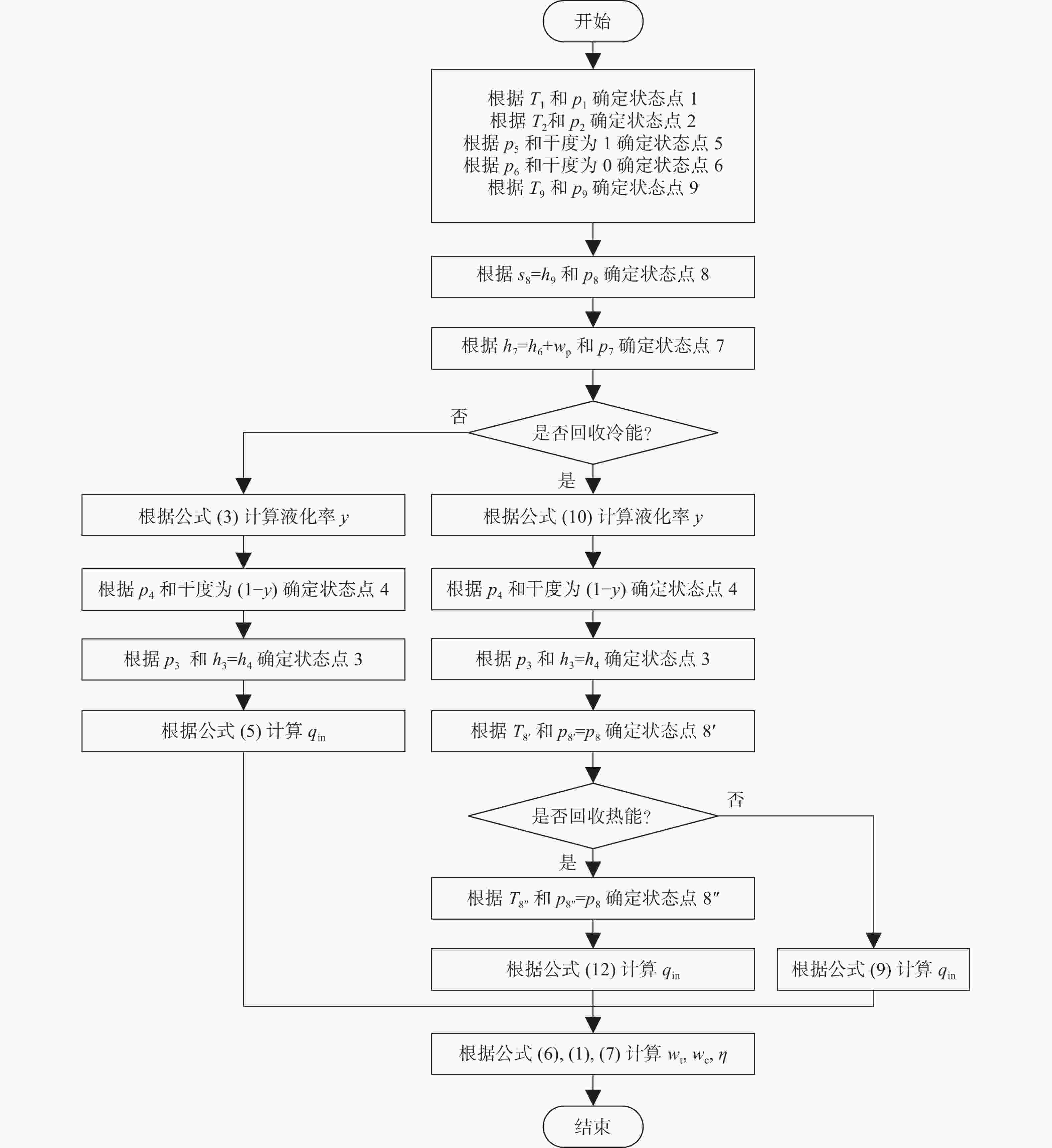
在相同的高压压力(8 MPa)和释能压力(5 MPa)下对比三种基本循环的性能,计算得到的每个状态点的热力学参数如表1、表2和表3所示。在3种模型中,常温和常压分别取为300 K和0.1 MPa,液化空气在常压下储存。即T1=T2=T9=300 K,p1=p4=p5=p6=p9=0.1 MPa,设定高压压力p2=p3=8 MPa,释能压力p7=p8=5 MPa。工质的热力学状态可以由任意两个独立的热力学参数确定,计算流程如图7所示。
状态点 T/K p/MPa h/[kJ·(kg)−1] s/[kJ·(kg)−1·K−1)] 1 300 0.1 426.30 3.891 2 300 8 409.85 2.583 3 157.49 8 196.82 1.569 4 81.49 0.1 196.82 2.467 5 81.61 0.1 204.72 2.563 6 78.79 0.1 −0.22 −0.00282 7 79.97 5 5.37 −0.00256 8 882.22 5 1041.80 3.891 9 300 0.1 426.30 3.891 wt/[kJ·(kg)−1] wp/[kJ·(kg)−1] wc/[kJ·(kg)−1] qin/[kJ·(kg)−1] y η 615.5 5.60 375.95 1036.43 0.063 0.078 Table 1. Thermodynamic parameters of the separate cycle
状态点 T/K p/MPa h/[kJ·(kg)−1] s/[kJ·(kg)−1·K−1)] 1 300 0.1 426.30 3.891 2 300 8 409.85 2.583 3 117.24 8 80.71 0.730 4 79.83 0.1 80.71 1.034 5 81.61 0.1 204.72 2.563 6 78.79 0.1 −0.22 −0.00282 7 79.97 5 5.37 −0.00256 8' 290 5 404.86 2.699 8'' 297 5 412.49 2.725 8 882.22 5 1041.80 3.891 9 300 0.1 426.30 3.891 wt/[kJ·(kg)−1] wp/[kJ·(kg)−1] wc/[kJ·(kg)−1] qin/[kJ·(kg)−1] y η 615.5 5.60 375.94 629.29 0.609 0.489 Table 3. Thermodynamic parameters of the cooling capacity and heat recovery cycle
表2相较于表1增加了一个状态点8',即冷能回收的最终状态点。点8'的温度由蓄冷效率决定,通常低于室温,这里取为290 K是一种比较理想的情况。对比两个表的数据可以发现冷能回收使得空气节流前(点3)的温度下降约40 K,比焓下降约116 kJ/kg。这使得等焓节流后的点4的比焓也相应下降,意味着T-s图上点4更接近液相点6,从而使液化率y提升了一个数量级。同时,动力循环需要输入的热量qin减少,而压缩机、泵的耗功以及膨胀机的做功保持不变,根据式(7)计算得到的循环效率η也提升了一个数量级。
状态点 T/K p/MPa h/[kJ·(kg)−1] s/[kJ·(kg)−1·K−1)] 1 300 0.1 426.30 3.891 2 300 8 409.85 2.583 3 117.24 8 80.71 0.730 4 79.83 0.1 80.71 1.034 5 81.61 0.1 204.72 2.563 6 78.79 0.1 −0.22 −0.00282 7 79.97 5 5.37 −0.00256 8' 290 5 404.86 2.699 8 882.22 5 1041.80 3.891 9 300 0.1 426.30 3.891 wt/[kJ·(kg)−1] wp/[kJ·(kg)−1]) wc/[kJ·(kg)−1] qin/[kJ·(kg)−1] y η 615.5 5.60 375.94 636.91 0.609 0.486 Table 2. Thermodynamic parameters of the cooling capacity recovery cycle
表3相较于表2增加了一个状态点8''
,即热能回收的最终状态点。点8'' 的温度由压缩热的温度决定,考虑到传热温差,此处取为297 K,低于等温压缩温度。对比表2和表3可以发现热能回收不影响液化率y,但会使动力循环需要输入的热量qin减少,从而提升循环效率η。由于林德液化循环是在常温下等温压缩,高于常温的热能仍然依赖外界输入,因此循环效率的提升不显著。 对比三种基本循环,分离式循环的液化率和循环效率均非常低,冷能回收循环在液化率和循环效率上均提升了一个数量级,冷能热能回收循环进一步提升了循环效率。因此,冷能热能回收循环是液化空气储能的优选方案。下文的分析也将针对冷能热能回收循环开展。
冷能热能回收循环中点1、9为常温常压状态,点5、6分别为常压下的饱和气和饱和液,这四个状态点是固定的。其余状态点根据高压压力(phigh)、释能压力(pdis)、冷能回收终点温度T8'以及热力学关系所确定。下面分别探究这三个独立的关键参数的影响。
-
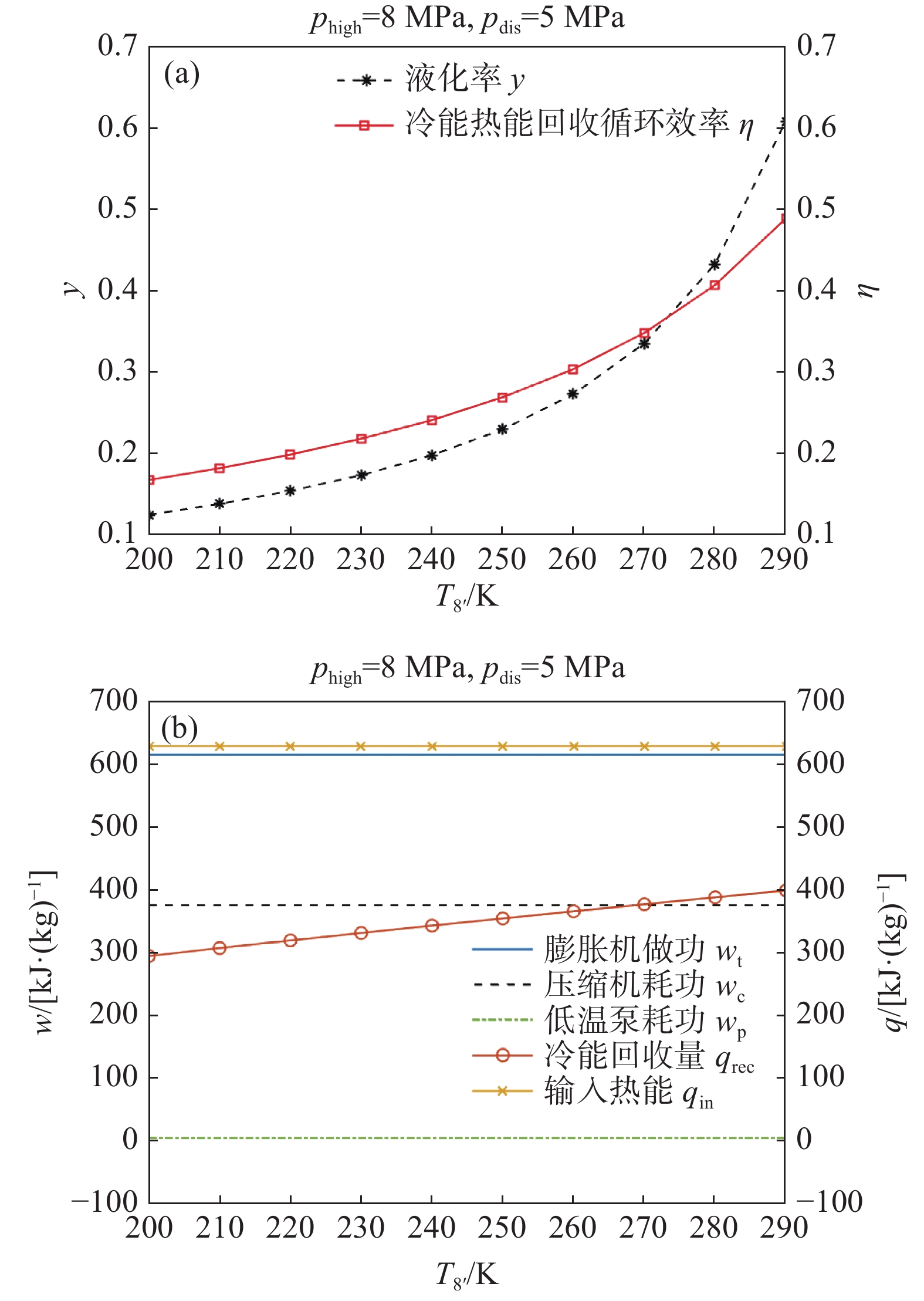
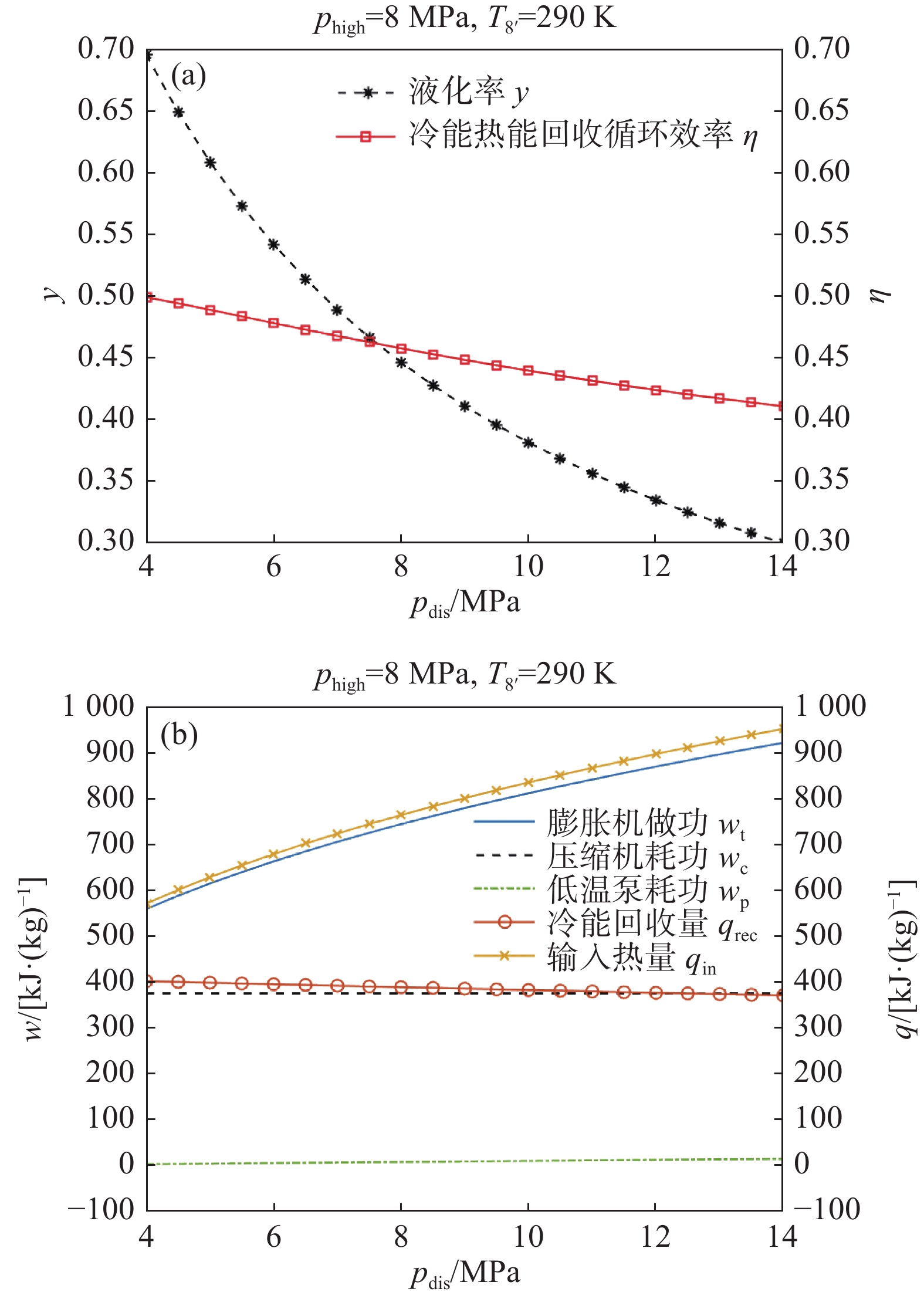
保持phigh为8 MPa、pdis为5 MPa,探究冷能回收终点温度的影响。计算结果如图8所示。图8(a)表明随着T8'从200 K升高到290 K,液化率从0.125增加到0.609,循环效率从0.168增加到0.489。图8(b)表明随着T8'升高,仅冷能回收量qrec升高,其余的功和热均保持不变。式(10)中分母减小,从而液化率增加;式(7)中因液化率增加导致分母减小,从而循环效率增加。
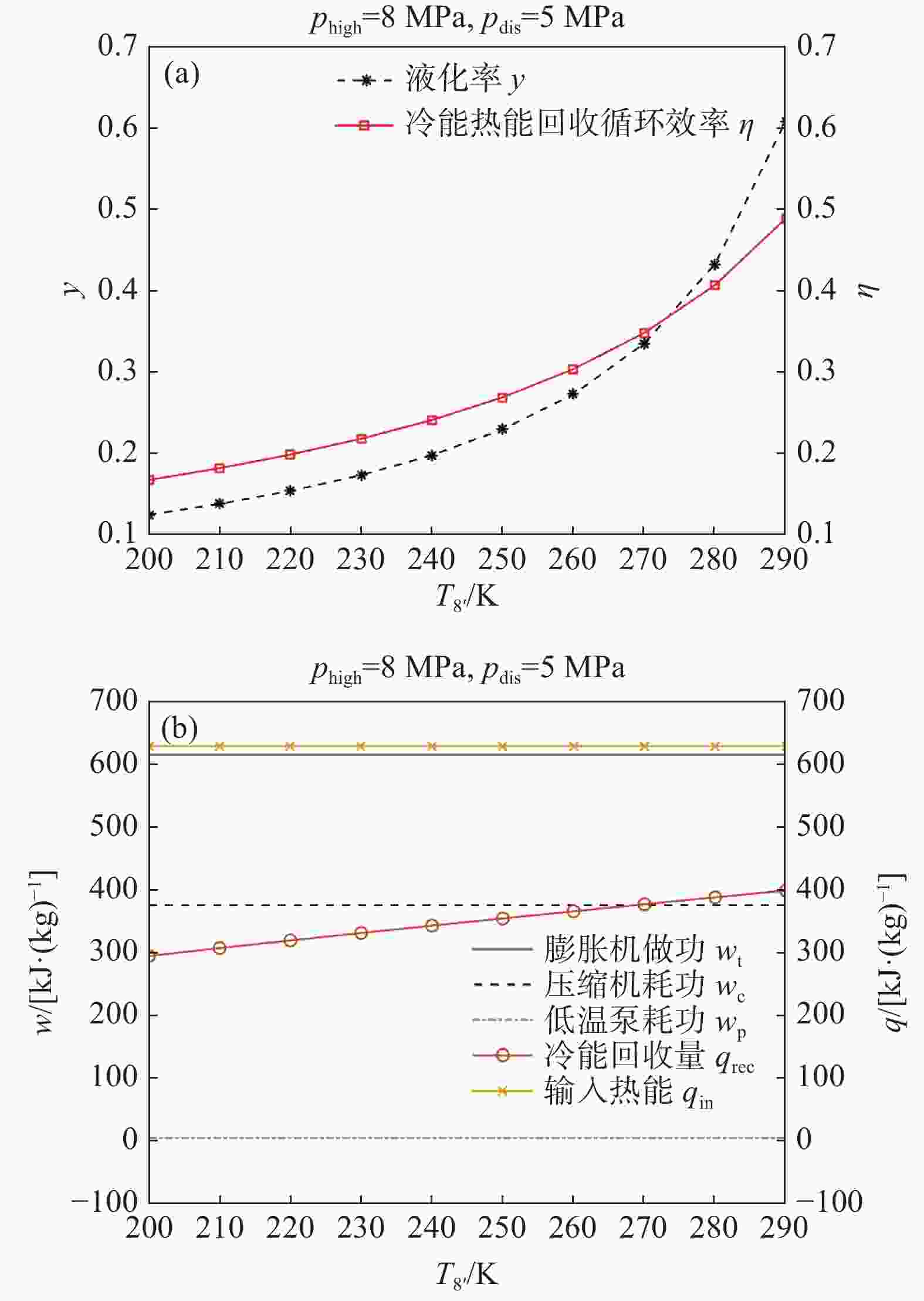
Figure 8. Effect of terminal temperature of cold energy recovery on: (a) liquid yield and cycle efficiency; (b) work and heat
由此可见,冷能回收越充分,越有利于提升循环效率。文章假设冷能直接通过液化循环的换热器回收,且换热器效率100%。在实际系统中,通常另外设置一个(组)蓄冷器,蓄冷效率随蓄冷时间的延长从95%下降至65%左右[22]。因此,开发高效的蓄冷方案是一个值得深入研究的方向[23]。
-
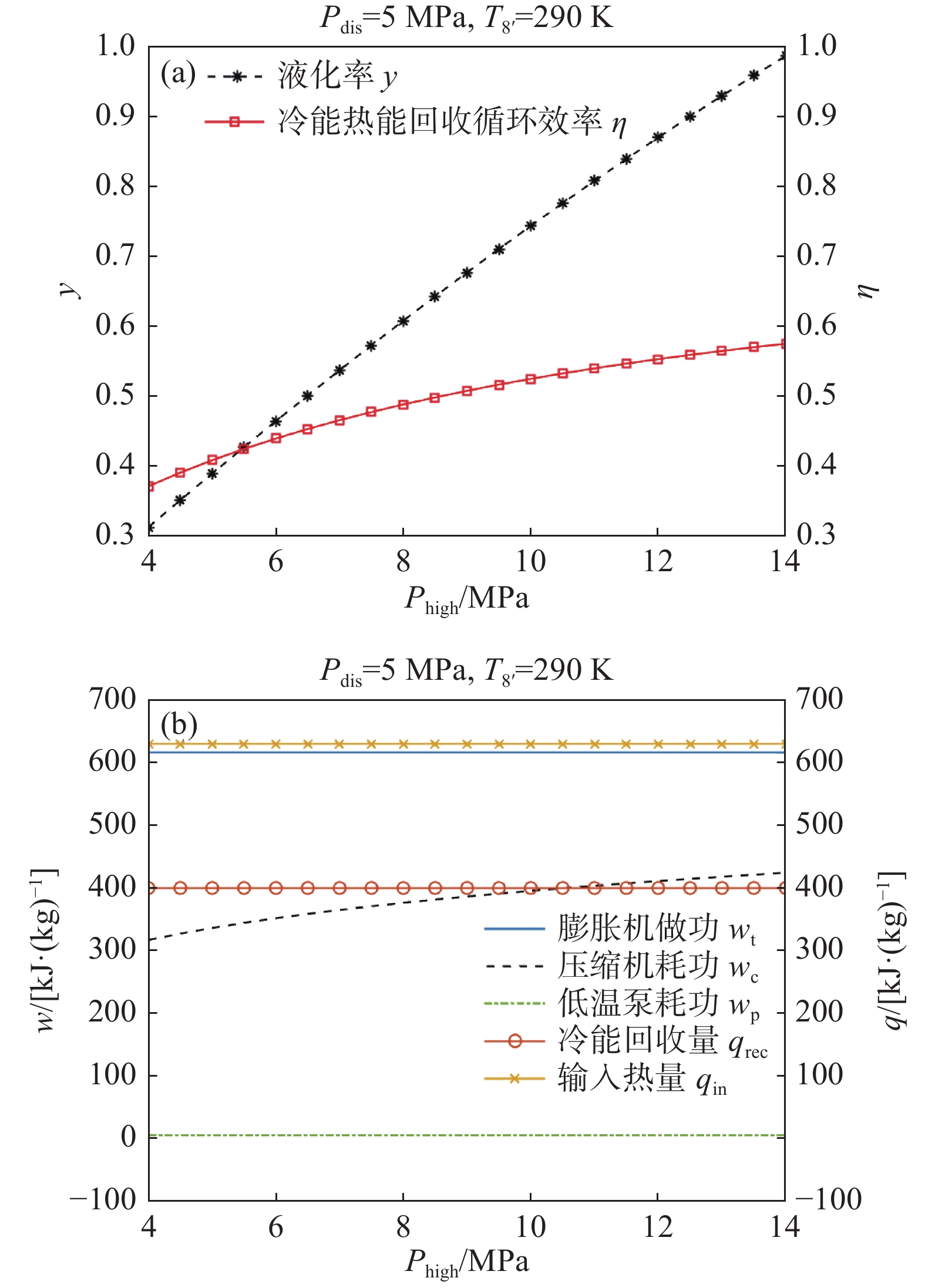
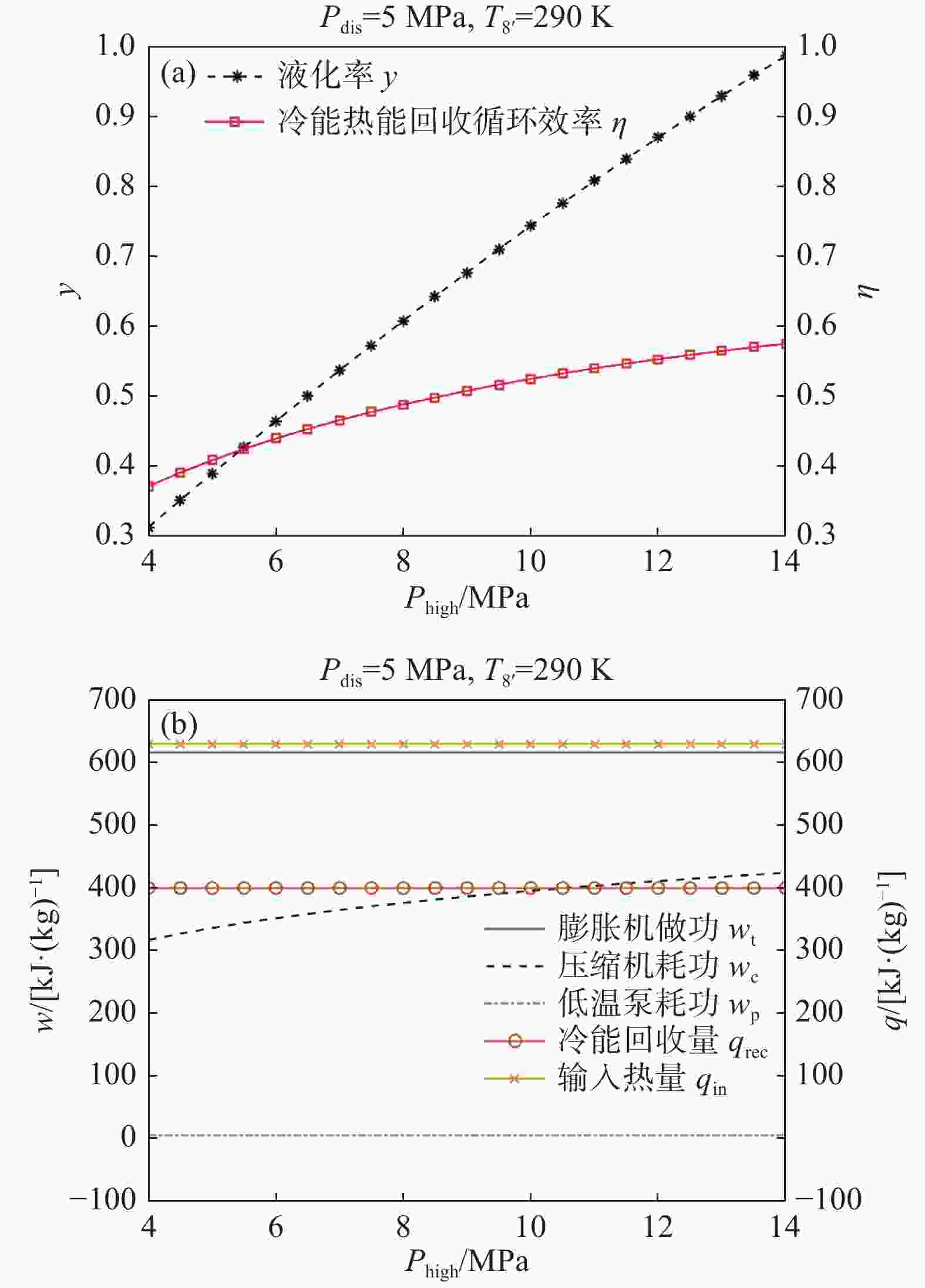
保持T8'为290 K,pdis为5 MPa,探究高压压力的影响。计算结果如图9所示。图9(a)表明随着phigh从4 MPa升高到14 MPa,液化率从0.314增加到0.986,循环效率从0.372增加到0.576。图9(b)表明随着phigh升高,仅压缩机耗功wc升高,其余的功和热均保持不变。
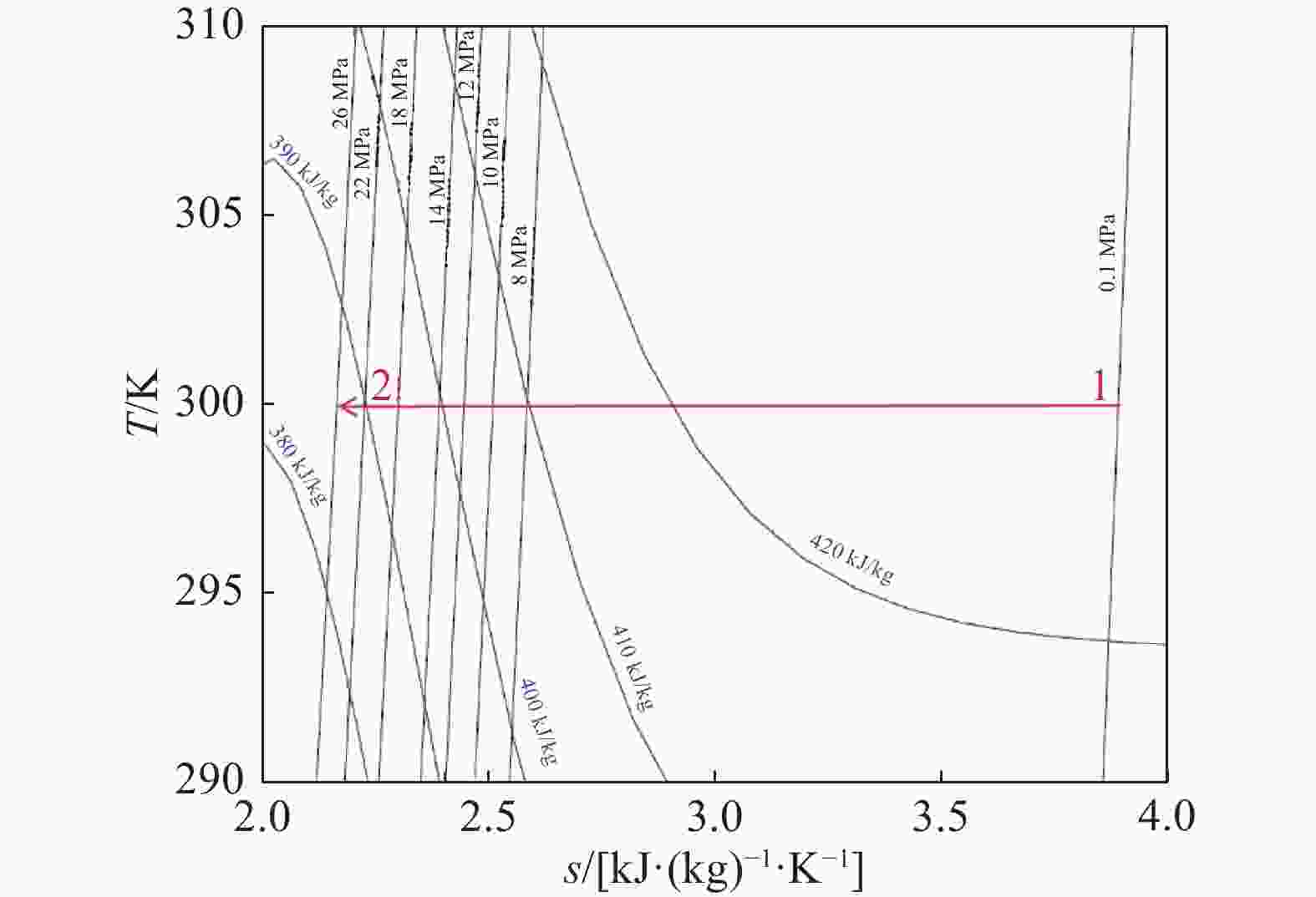
在液化率的表达式(10)中,高压压力仅影响压缩终点的比焓h2。由空气的T-s图(图10)可知,随着高压压力升高,压缩终点(点2)逐渐左移,h2逐渐减小。由式(10)可知,在其他物理量保持不变的情况下,h2越小使得液化率越大。由此可知,高压压力通过影响压缩过程的比焓降来影响液化率。
在循环效率的表达式(7)中,高压压力影响压缩机耗功和液化率。图9表明随着高压压力升高,液化率的增长率远大于压缩机耗功的增长率,即单位质量液空的耗功(wc/y)减小。式(7)的分母减小,使得循环效率升高。
尽管高压压力升高对循环效率有益,但在实际系统设计中,要考虑换热器承压、高压压缩机成本等问题,目前空气液化循环的高压压力通常不超过10 MPa[24]。
-
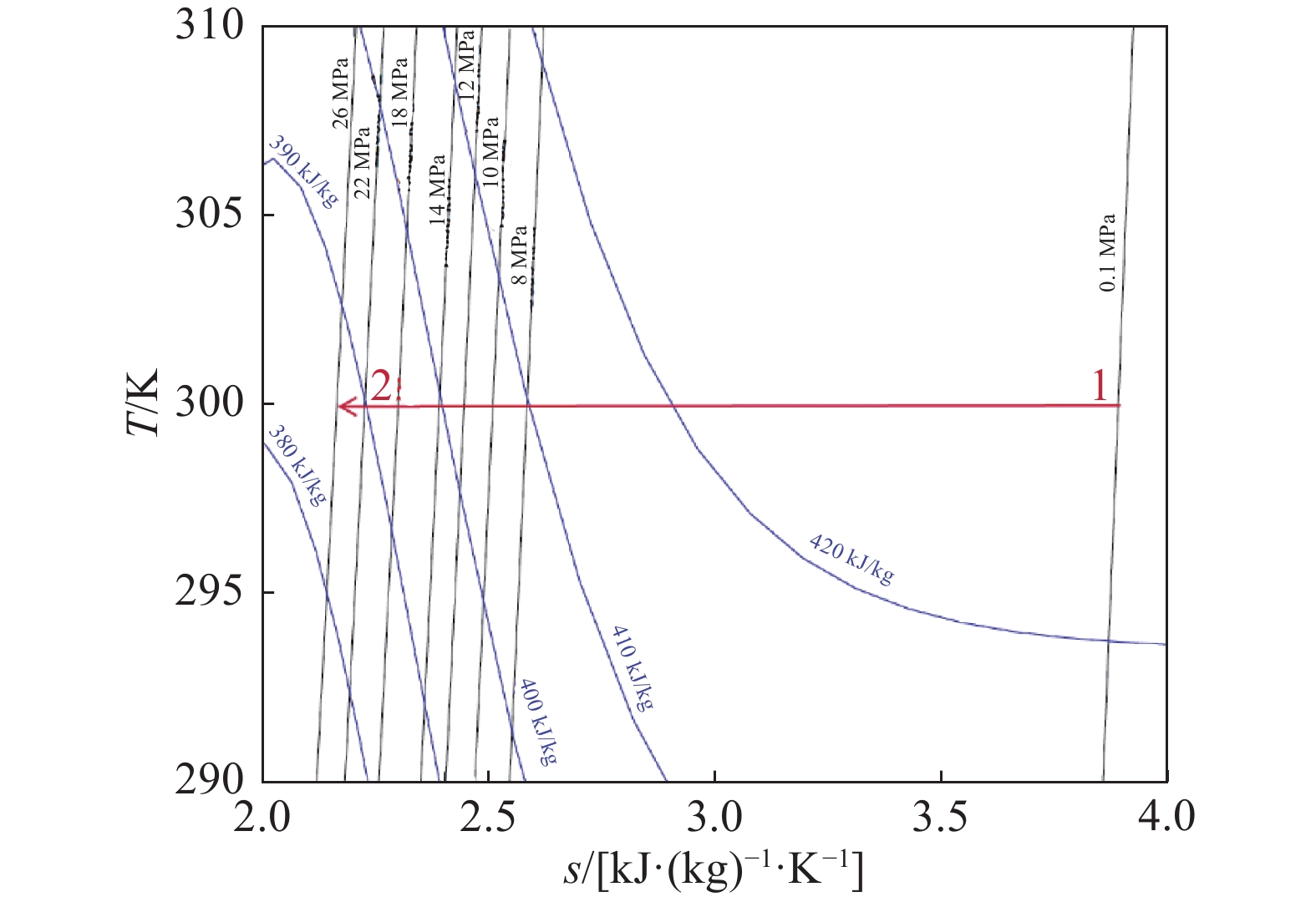
保持T8'为290 K、phigh为8 MPa,探究释能压力的影响。计算结果如图11所示。图11(a)表明随着pdis从4 MPa升高到14 MPa,液化率从0.695降低到0.300,循环效率从0.499降低到0.411。图11(b)表明随着pdis升高,仅压缩机耗功wc保持不变,膨胀机做功和低温泵耗功升高,冷能回收量降低,输入热量增加。
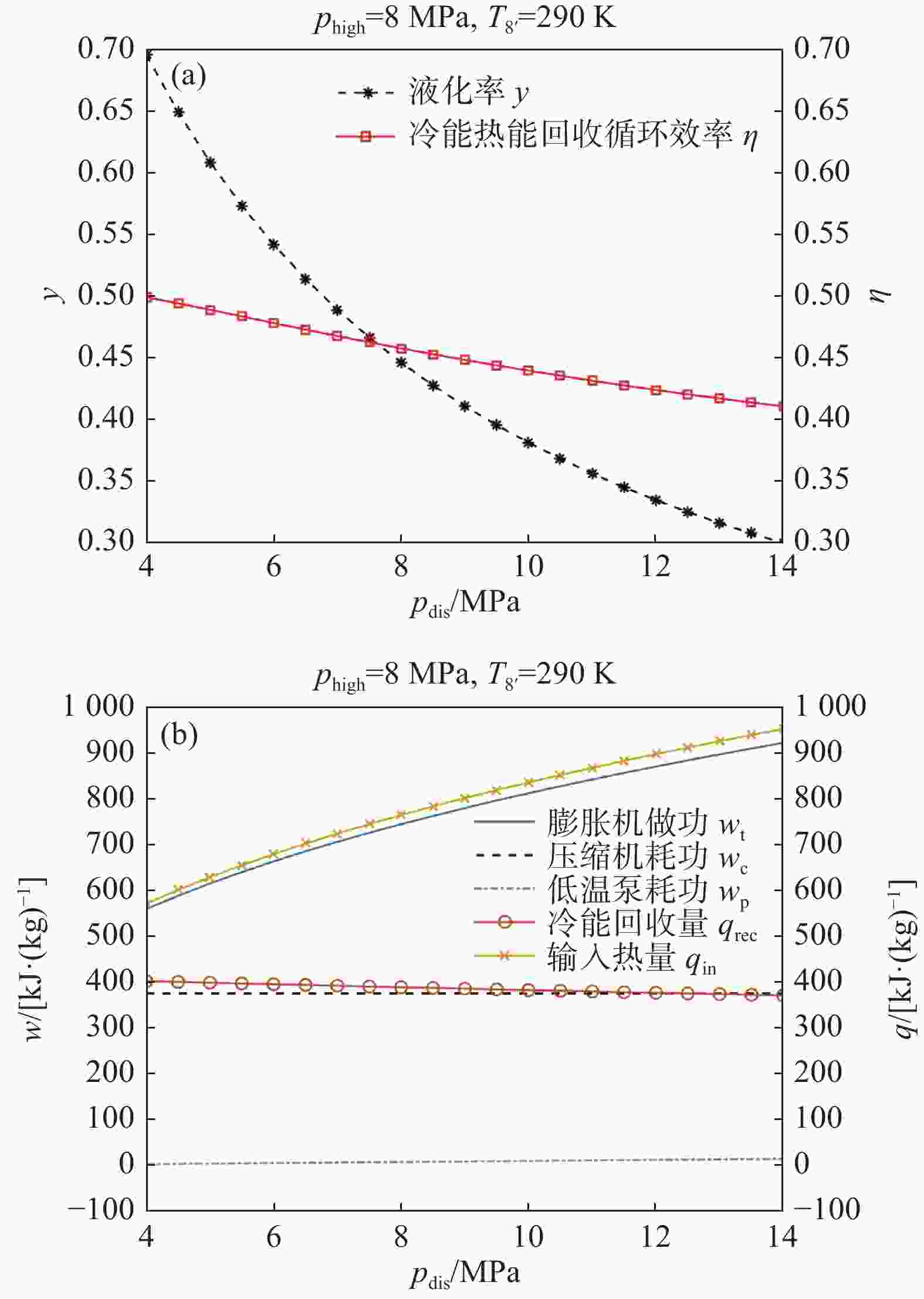
Figure 11. Effect of discharge pressure on: (a) liquid yield and cycle efficiency; (b) work and heat
与phigh升高使h2降低类似,pdis升高使h8'降低,从而回收的冷能qrec减少。液化率的表达式(10)中分母增大,液化率减小。
在循环效率的表达式(7)中,分子分母同时增加,然而分母的增加幅度等大,使循环效率降低。
尽管释能压力升高不利于循环效率,但一味降低释能压力也不可取。这是因为较低的释能压力对应较小膨胀机做功量。因此,要根据液化空气储能系统对释能功率和循环效率的综合需求来进行取舍,选择合适的释能压力。
-
通过比较分离式循环、冷能回收循环、冷能热能回收循环的热力学性能,揭示了冷能回收对液化率的提升极为关键,冷能热能回收循环的效率最高,是值得推荐的一种循环方案。
针对冷能热能回收循环通过控制变量法探究了三个关键参数:冷能回收终点温度、高压压力、释能压力对液化率和循环效率的影响机制。结果表明液化率和循环效率正相关。液化率与循环效率随冷能回收终点温度(冷能回收量)的增加而升高、随高压压力的升高而升高、随释能压力的升高而下降。液化空气储能系统应配备尽可能高效的蓄冷装置、在系统允许的范围内选择尽可能高的高压压力、释能压力的确定则要对循环效率和功率做出取舍。
尽管文章的结论是在林德液化循环加朗肯循环的基础上得到的,但对于其他液化循环和动力循环的组合同样适用。文章冷能和热能均来自系统内部,如果对系统外的冷能和热能(如LNG冷能和工业余热)加以利用,可以进一步提升循环效率。
Thermodynamic Analysis of Basic Cycles of Liquid Air Energy Storage System
doi: 10.16516/j.gedi.issn2095-8676.2022.04.007
- Received Date: 2022-03-07
- Accepted Date: 2022-09-29
- Rev Recd Date: 2022-04-14
- Available Online: 2022-12-25
- Publish Date: 2022-12-23
-
Key words:
- liquid air energy storage /
- thermodynamic analysis /
- cooling capacity and heat recovery /
- liquid yield /
- cycle efficiency
Abstract:
| Citation: | SUN Xiao, ZHU Guangtao, PEI Aiguo. Thermodynamic Analysis of Basic Cycles of Liquid Air Energy Storage System[J]. SOUTHERN ENERGY CONSTRUCTION, 2022, 9(4): 53-62. doi: 10.16516/j.gedi.issn2095-8676.2022.04.007 |


















 DownLoad:
DownLoad: