-
随着全球化石能源枯竭和温室效应的加剧,开发和利用新型可再生能源迫在眉睫,而海洋中蕴含丰富的可再生能源,其中风能和波浪能以其能量储备多,能量密度高,分布广泛成为各国研究的重点。对于单一形式海洋能源开发存在效率低成本高的难题,而海洋多能互补发电技术有望解决这一难题。为了助力碳中和,发展清洁可再生能源,多能互补联合开发,实现立体用海,集约用海,资源利用最大化,将波能浮子WEC(Wave Energy Converter)阵列与海上浮式风机平台结合,两者共享支撑平台、系泊系统和电缆传输系统降低成本支出,联合开发海上风能和波浪能,提高能源利用率,节约用海空间[1-3]。
史玉涛等人[4]对阵列式波浪能发电原理、系统构成及工程应用实例进行了梳理分类,认为阵列式波浪能发电可以实现大规模发电、连续稳定电能输出。周斌珍等人[5]研究了风浪联合发电系统水动力学数值模拟方法,包括线性频域、线性时域、势流非线性方法,以及基于Navier-Stokes方程的黏性方法等,从计算效率上看,线性频域方法最优。胡缘等人[6]通过仿真实验显示,在相同海况条件下,漂浮平台对于浮子的振荡响应有一定的影响,从而影响装置整体的波浪能采集效率。顾煜炯等人[7]通过数值仿真和海况试验,表明进行合理优化布置的阵列浮子对多浮体波浪能发电装置系统的稳定高效功率输出有很大作用。王淇[8]提出了一种新型浮式风浪能混合利用系统概念设计。胡俭俭等人[9]设计了一种浮式风机平台与多波能装置耦合系统,并进行了频域研究,发现不同阵列布置下,浮子直径吃水比越大,能量俘获性能越好,同时浮子的加入,使平台纵摇力矩减小。
因此本文以波能浮子阵列-浮式风机平台集成系统为研究对象,考虑最优PTO(能量俘获系统Power Take Off)阻尼条件下,对波浪能装置进行水动力分析和俘获功率优化。探究在基于海上风电场实测波浪条件下波能浮子阵列发电功率优化,不同的波能装置外形尺寸和固有周期对波浪能装置输出功率的影响并考虑浮子的经济性。
-
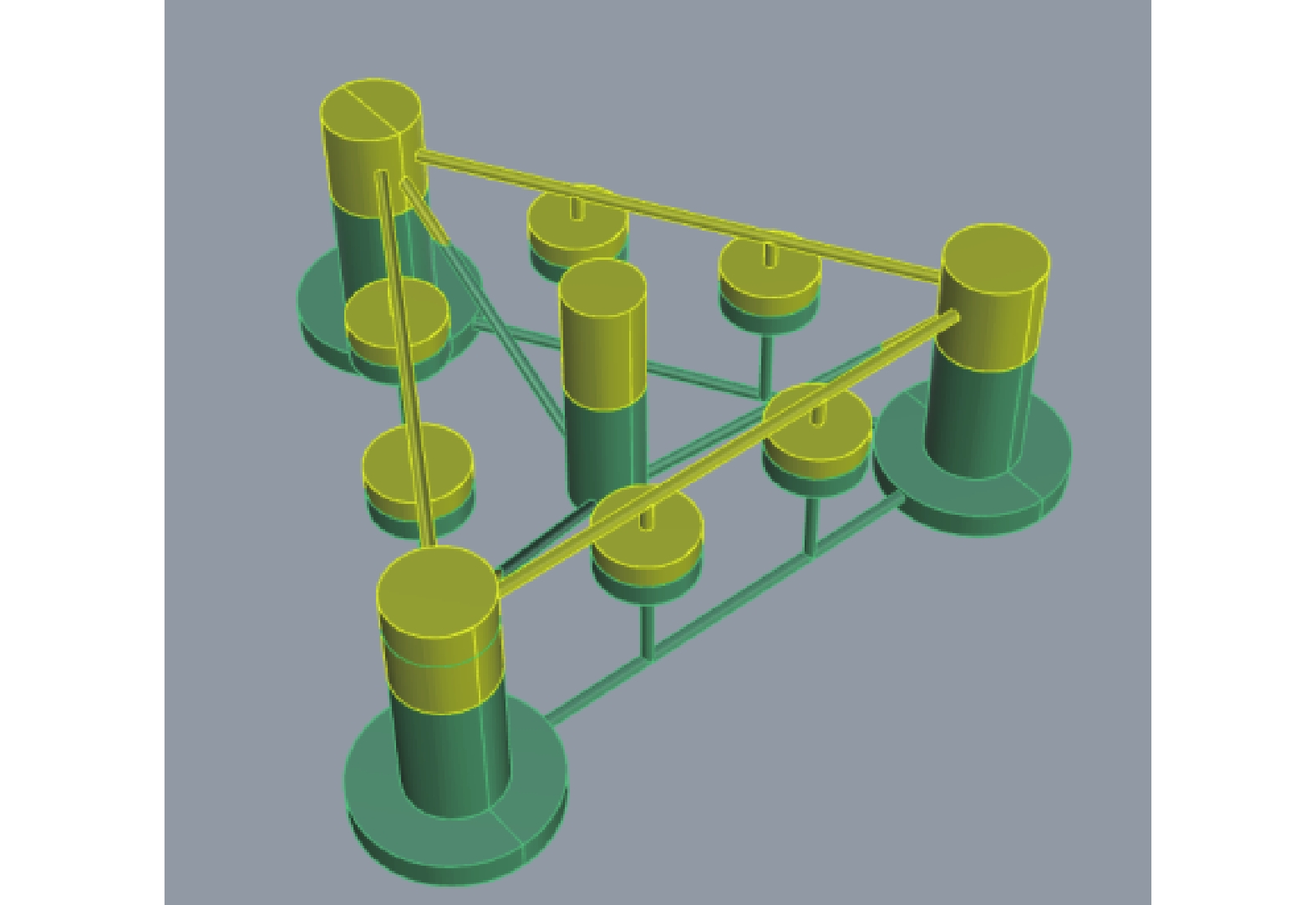
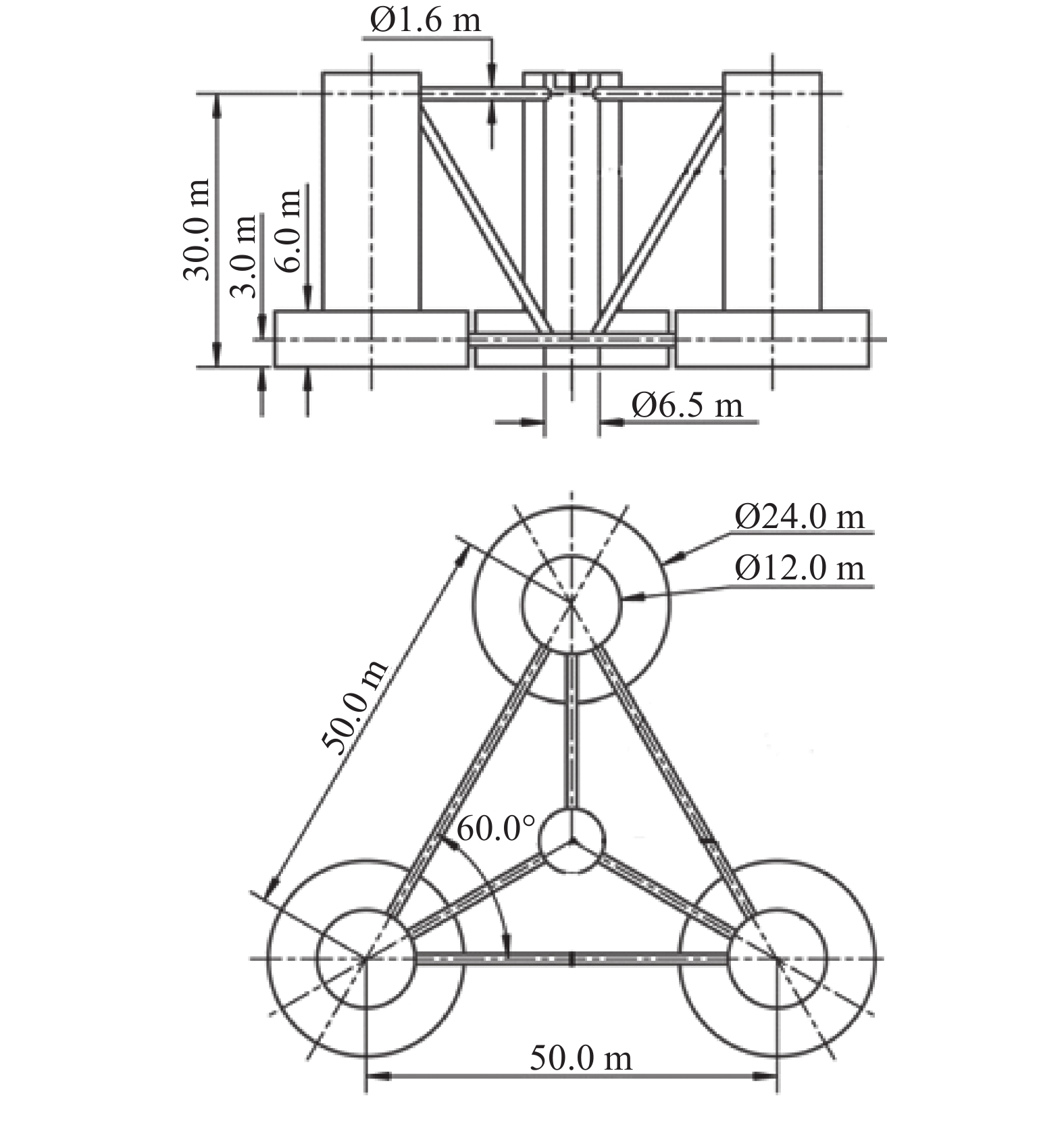
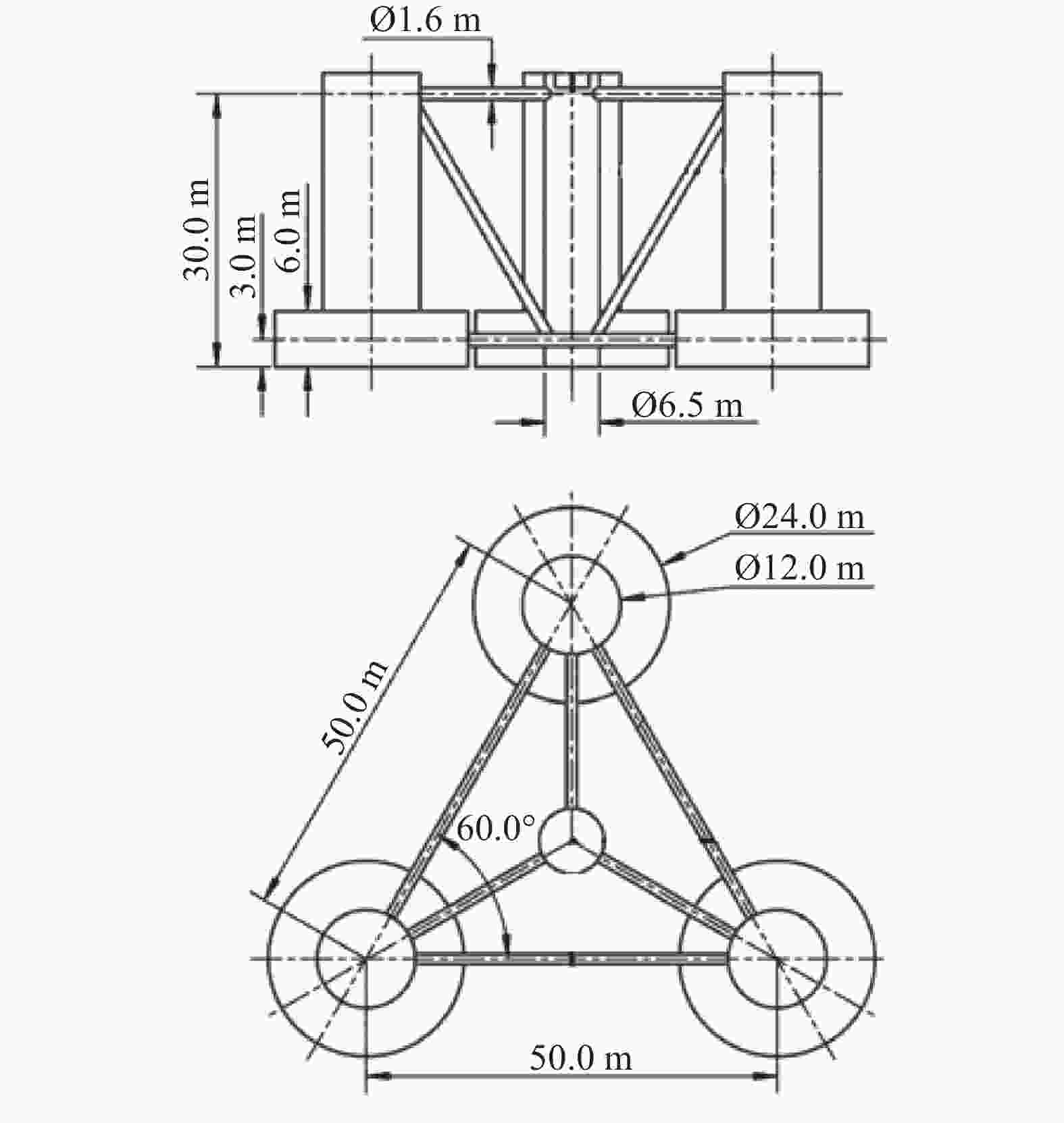
本文选择水线面面积小、稳定性好、作业水深范围广、能够很好地适应我国的海域特点的OC4-deepC半潜平台与波能浮子结合[10-11],如图1所示。
波浪能装置选择典型的圆柱形的点吸式作为研究对象。点吸式波能装置具有转换效率高、建造成本低、输出电能稳定、易于平台结合的优点[12-14]。
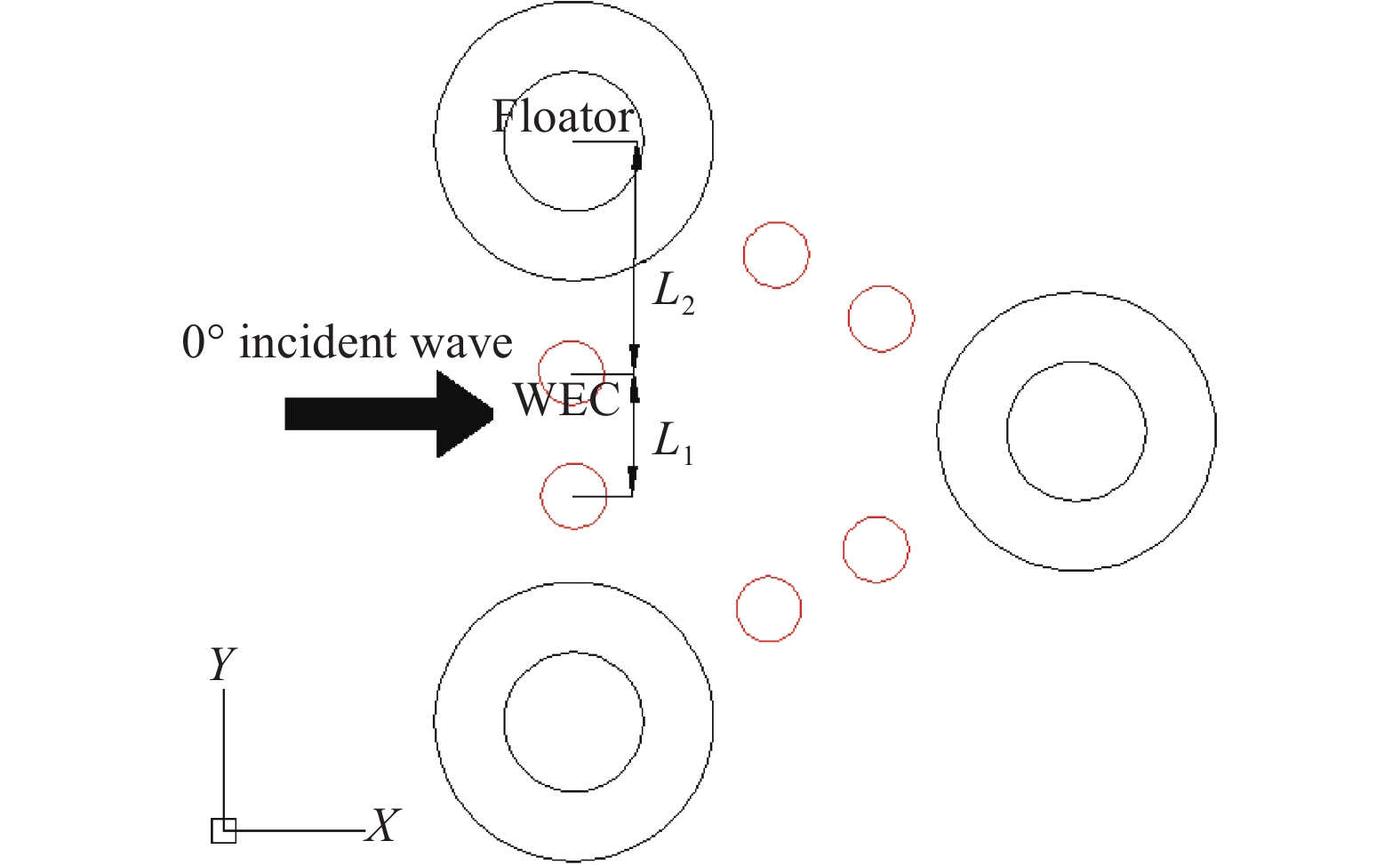
因此本文以波浪能浮子阵列-漂浮式风机平台集成系统(如图2所示)为研究对象,通过水动力计算软件SESAM-HydroD建立频域分析模型,得到水动力系数附加质量、辐射阻尼、波浪激振力等,利用Python二次开发,考虑最优PTO阻尼条件下,求解多体耦合运动方程,探究在目标海域波浪情况下,波能浮子外形尺寸和共振周期对集成系统发电功率的影响。目前仅考虑平台与波能浮子阵列间的耦合作用,尚未考虑风机的影响。
-
本文选择广东省某风电场海域为波能阵列-浮式平台集成系统布设目标海域,对该海域观测到的波浪数据进行整理和统计分析,该风电场海域的波浪分布情况如表1所示,由表1可知,该海域波浪主要波高1.0~3.0 m,主要波浪周期集中在3.0~7.0 s,占整个波浪周期的99%以上,平均波浪周期T=4.69 s。
H/m T/s 1 2 3 4 5 6 7 8 9 10 11 12 13 Total 12.5 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 12.0 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.001 0.000 0.000 0.000 0.001 11.5 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 11.0 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.001 0.000 0.000 0.000 0.001 10.5 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 10.0 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.001 0.000 0.001 0.000 0.000 0.001 9.5 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.001 0.001 0.000 0.000 0.002 9.0 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.001 0.002 0.002 0.001 0.000 0.006 8.5 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.001 0.001 0.000 0.000 0.003 8.0 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.002 0.003 0.000 0.000 0.000 0.005 7.5 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.001 0.004 0.002 0.000 0.000 0.000 0.007 7.0 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.003 0.006 0.007 0.002 0.000 0.000 0.018 6.5 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.008 0.013 0.003 0.000 0.000 0.000 0.024 6.0 0.000 0.000 0.000 0.000 0.000 0.000 0.002 0.012 0.019 0.002 0.001 0.000 0.000 0.035 5.5 0.000 0.000 0.000 0.000 0.000 0.000 0.006 0.023 0.014 0.003 0.001 0.000 0.000 0.048 5.0 0.000 0.000 0.000 0.000 0.000 0.002 0.010 0.050 0.010 0.000 0.000 0.000 0.000 0.072 4.5 0.000 0.000 0.000 0.000 0.000 0.006 0.050 0.053 0.020 0.003 0.001 0.000 0.000 0.133 4.0 0.000 0.000 0.000 0.000 0.000 0.017 0.131 0.032 0.013 0.003 0.001 0.001 0.000 0.198 3.5 0.000 0.000 0.000 0.000 0.003 0.112 0.191 0.026 0.010 0.004 0.001 0.002 0.001 0.350 3.0 0.000 0.000 0.000 0.000 0.020 0.610 0.158 0.028 0.011 0.005 0.002 0.003 0.002 0.840 2.5 0.000 0.000 0.000 0.000 0.937 2.571 0.186 0.040 0.013 0.013 0.007 0.003 0.000 3.770 2.0 0.000 0.000 0.000 0.081 11.280 3.651 0.266 0.095 0.049 0.027 0.006 0.000 0.000 15.460 1.5 0.000 0.000 0.000 13.400 22.790 2.190 0.535 0.135 0.020 0.001 0.000 0.000 0.000 39.080 1.0 0.000 0.000 2.023 30.060 5.503 1.567 0.228 0.003 0.001 0.000 0.000 0.000 0.000 39.380 0.5 0.000 0.000 0.158 0.250 0.140 0.022 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.570 Total 0.000 0.000 2.181 43.790 40.690 10.750 1.763 0.510 0.206 0.081 0.025 0.008 0.004 100.000 Table 1. Joint probability distribution Sj of wave height Hj and wave period Tj in a wind farm in Guangdong
-
由于OC4-DeepC平台固有周期远离风电场海域的谱峰周期,其垂荡运动相对于波能浮子来说很小,因此本文考虑将平台固定,波能浮子仅沿支撑杆件做垂荡运动。基于以上假设,建立波能浮子阵列中第i个浮子的运动方程:
$$ \begin{split} &\left[-{\omega }^{2}({m}_{i}+{a}_{ii})+i\omega \left({b}_{ii}+{B}_{{\rm{opt}},i}\right)+{C}_{i}\right]{z}_{i}+\\&\sum _{j=1,j\ne i}^{N}\left({-{\omega }^{2}{a}_{ij}+i\omega b}_{ij}\right){z}_{j}={F}_{{\rm{ex}},i} \end{split} $$ (1) 采用专业软件HydroD计算式(1)中的水动力系数aii、bii、aij、bij及Fex,i。
式中:
aii,bii ——第i个浮子的垂荡运动产生的附加质量、辐射阻尼;
aij,bij ——第j个浮子的运动对第i个浮子产生的附加质量、辐射阻尼;
mi,Ci,Fex,i ——第i个浮子的质量、恢复力和波浪激振力;
ω,zi,zj ——频率、第i、j个浮子的垂荡运动幅值。
采用单个波能装置的线性最优阻尼Bopt:
$$ {B}_{{\rm{opt}},i}=\sqrt{\frac{{\left(\left({m}_{i}+{a}_{ii}\right){\omega }^{2}-{C}_{i}\right)}^{2}}{{\omega }^{2}}+{{b}_{ii}}^{2}} $$ (2) 第i个浮子在最优PTO阻尼下的俘获功率Pi(
$ \omega $ )为:$$ {P}_{i}\left(\omega \right)=\frac{1}{2}{{\omega }^{2}B}_{{\rm{opt}},i}{\left|{z}_{i}\right|}^{2} $$ (3) 联合(1)~(3),求解得到波能阵列的第i个浮子的垂荡运动响应zi和俘获功率Pi。
波能阵列的发电功率Ptotal(T)为:
$$ {P}_{{\rm{total}}}\left(T\right)={\sum }_{i=1}^{N}{P}_{i}\left(T\right) $$ (4) 为了更简单衡量波能浮子的经济性,引入公式(5)波能阵列的功率体积比Pav(T):
$$ {P}_{{\rm{av}}}\left(T\right)=\frac{{P}_{{\rm{total}}}\left(T\right)}{\rho {V}_{{\rm{total}}}} $$ (5) 式中:
N ——浮子个数(个);
Vtotal ——N个浮子总体积(m³),Pav越小,则代表经济性更好,这里假定单位体积的波能装置的成本是一致的。
-
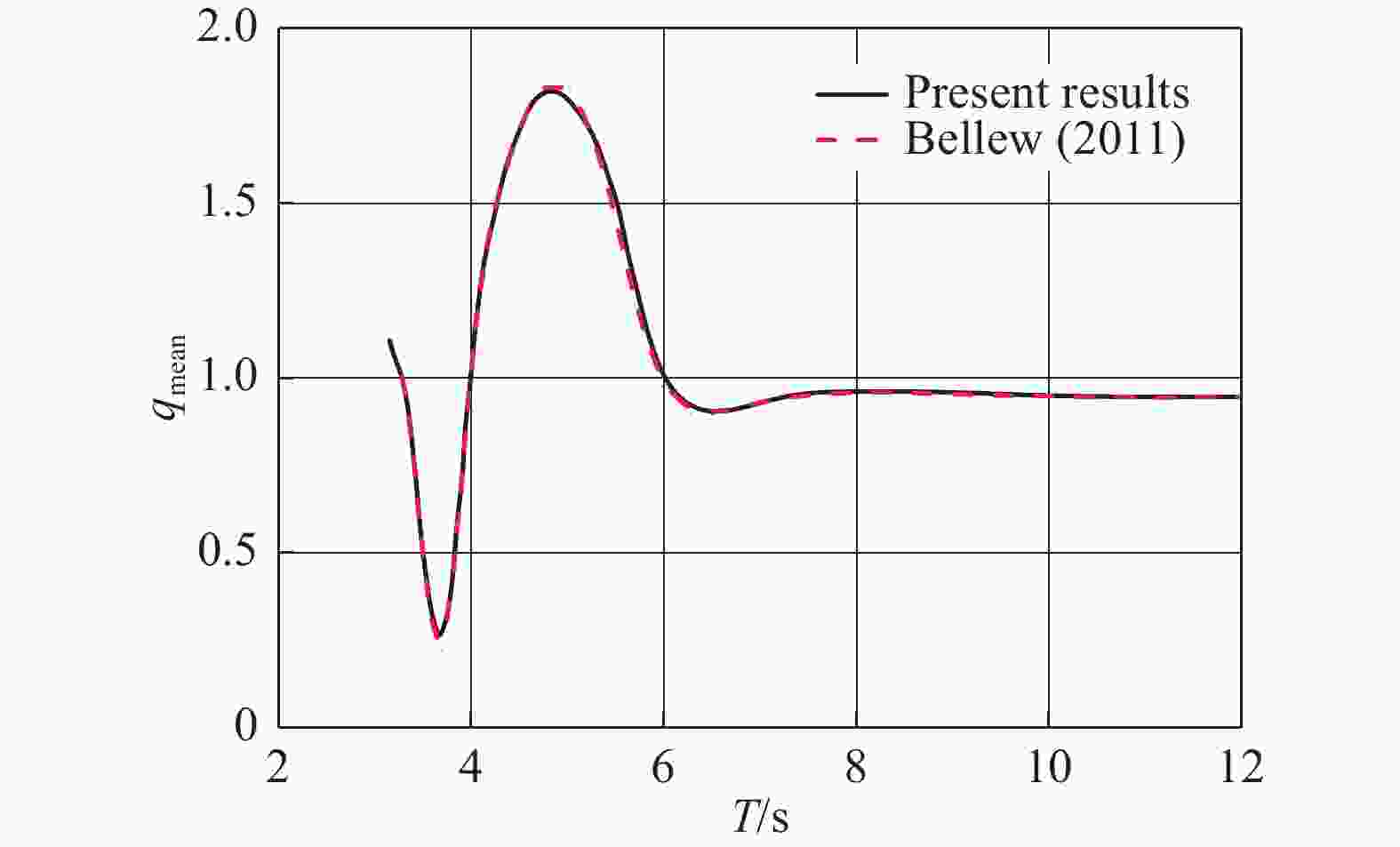
定义相互作用因子qmean,用于衡量相互作用对波浪能浮子WEC(Wave Energy Converter)阵列中功率吸收的影响。其定义为耦合波浪能浮子阵列WEC总功率与单个单独放置波浪能浮子WEC的功率的N倍的比值:
$$ {q}_{{\rm{mean}}}\left(T\right)=\frac{{P}_{{\rm{total}}}\left(T\right)}{N\times {P}_{{\rm{isolated}}}\left(T\right)} $$ (6) 式中:
Pisolated(T)——单个单独放置波浪能浮子WEC的最优发电功率(kW)。
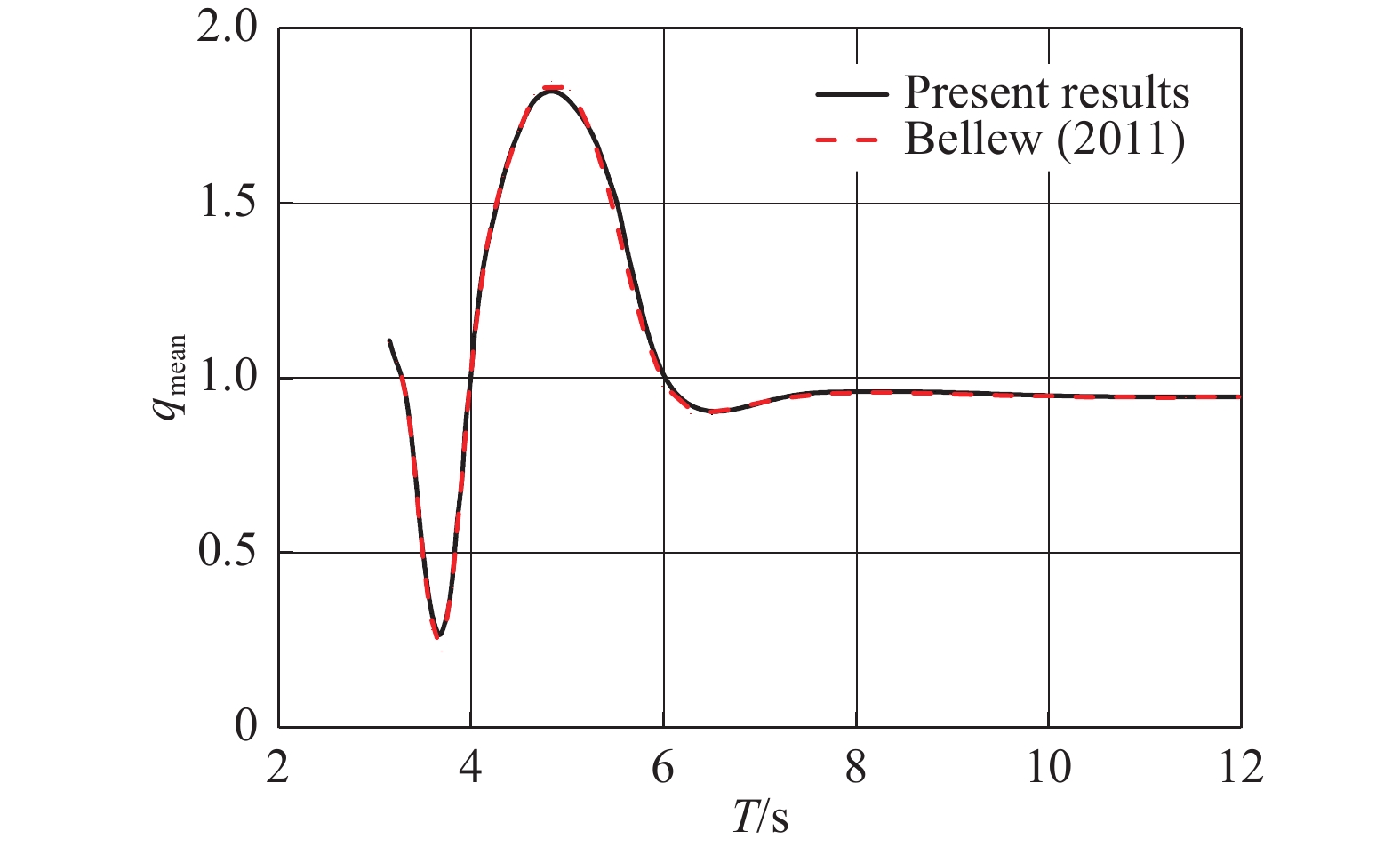
通过模拟文献中Bellew的5×1半球形WEC阵列来验证HydroD频域模型[13],如图3所示。图3为最优PTO阻尼下5×1半球形WEC阵列的相互作用因子qmean的对比图,可以看出,通过HydroD建立的频域分析模型数值结果与已发表文献结果吻合良好,验证了模型的正确性。
-
HU等人[15]采用无量纲原则推导出无量纲固有频率与固有频率的关系式,指定固有频率ωp可得到随直径吃水比2r/d变化的圆柱形浮子的吃水d;即可以根据已知海况计算指定固有频率下,不同直径吃水比2r/d的圆柱形波浪能浮子WEC的吃水深度d。
$$ d=\mathrm{g}{\left(\dfrac{{\overline{\omega }}_{n}\left(\dfrac{2r}{d}\right)}{{\omega }_{{\rm{p}}}}\right)}^{2} $$ (7) $$ {\omega }_{{\rm{p}}}=\dfrac{2{\text{π}}}{{T}_{{\rm{p}}}} $$ (8) 基于目标海域的波浪特征,波浪周期主要集中在3.0~7.0 s,其中4.0~5.0 s波浪周期占比80%以上,因此假定目标海域的平均波浪T=4.69 s为波能浮子固有周期Tp,根据无量纲原则,计算得到一系列2r/d对应的浮子吃水d和半径r。
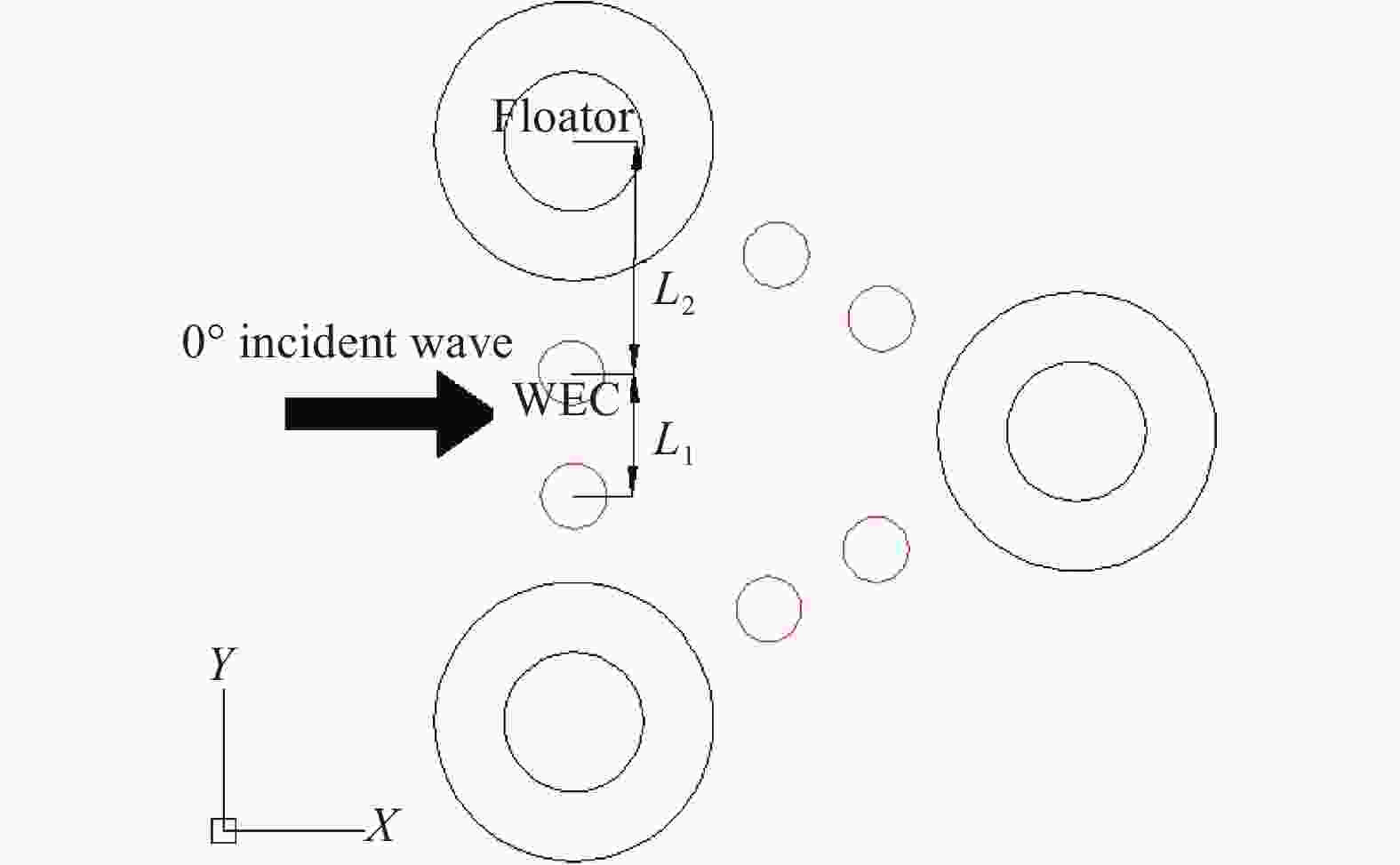
设计浮子间圆心距L1=4 r,波浪能浮子WEC与平台浮筒间间距L2≥R+3 r,选择最多可布置波浪能浮子数N=6的浮子进行水动力分析,探究不同直径吃水比的波浪能浮子WEC的发电性能和经济性,波浪能浮子WEC具体参数见表2,布置方式如图4所示。
2r/d r d L1 L2 1.6 2.80 3.50 11.20 19.40 1.8 3.05 3.39 12.20 18.90 2.0 3.29 3.29 13.14 18.43 2.2 3.51 3.19 14.04 17.98 Table 2. Geometric parameters of WEC
-
在水动力分析软件HydroD建立平台和浮子的耦合模型,进行频域分析得到平台-浮子的水动力系数,同时考虑单个浮子公式最优Bopt,求解运动方程(1),得到各个浮子的垂向响应Zi,带入公式(3)(4)得到各个浮子的发电功率Pi和浮子的总发电功率Ptotal。
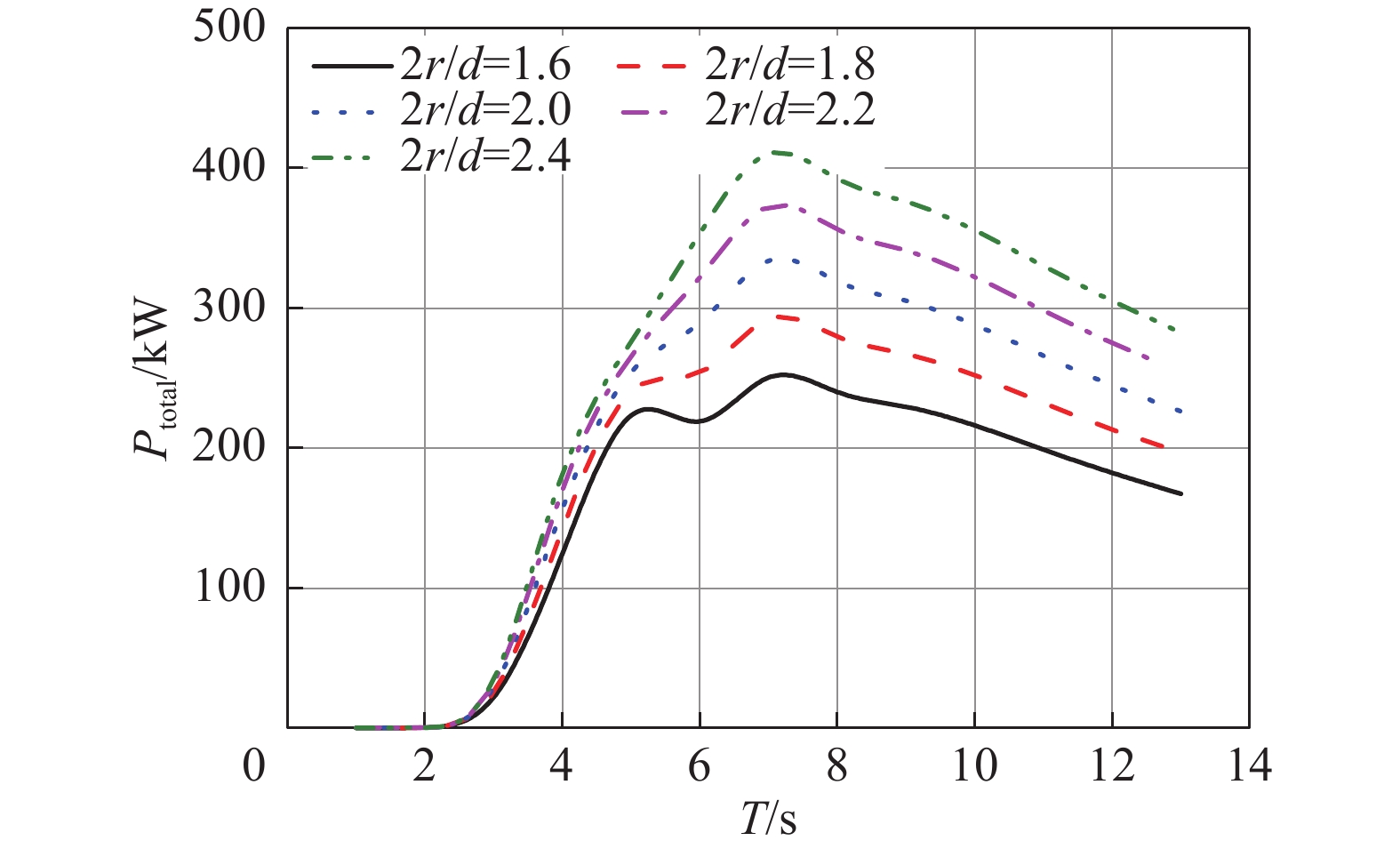
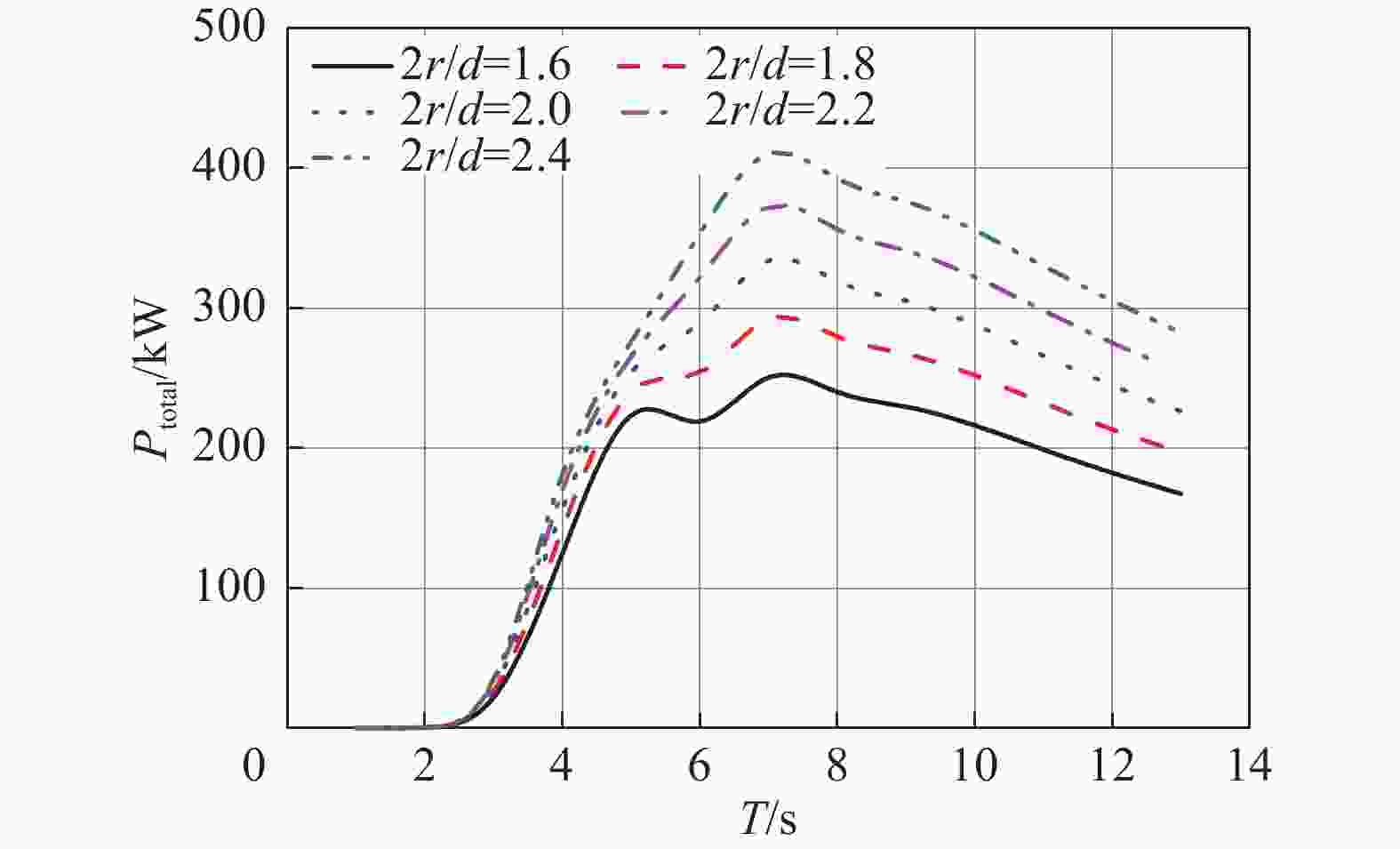
图5反映了不同2r/d下波能浮子阵列总发电功率Ptotal随波浪周期变化关系。由图可知,同一2r/d的波能浮子阵列的总发电功率Ptotal随着波浪周期的增加而先增加后减小。同时,随着浮子2r/d的增加浮子的总发电功率Ptotal峰值是逐渐增加,频带宽度也略有增加。
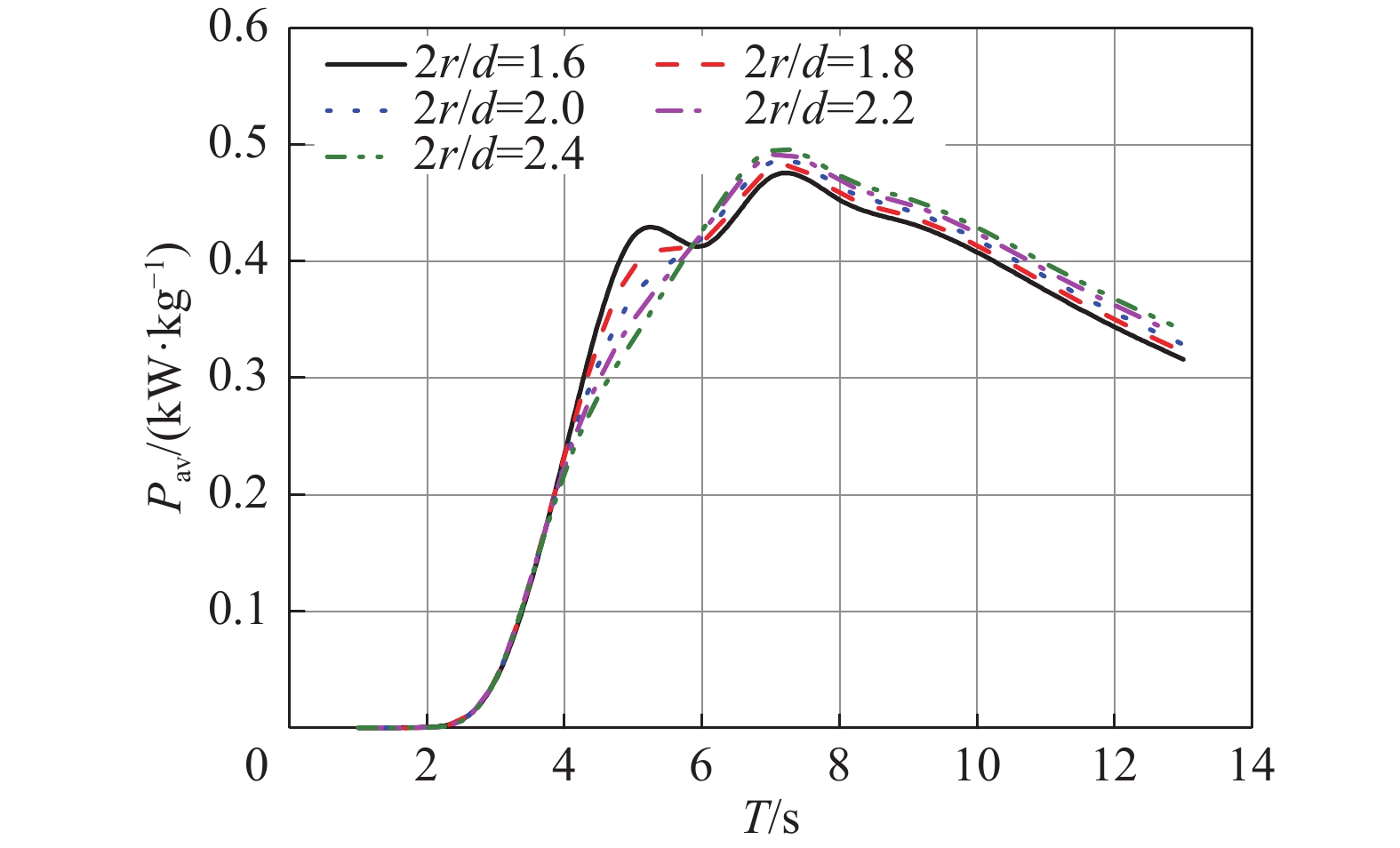
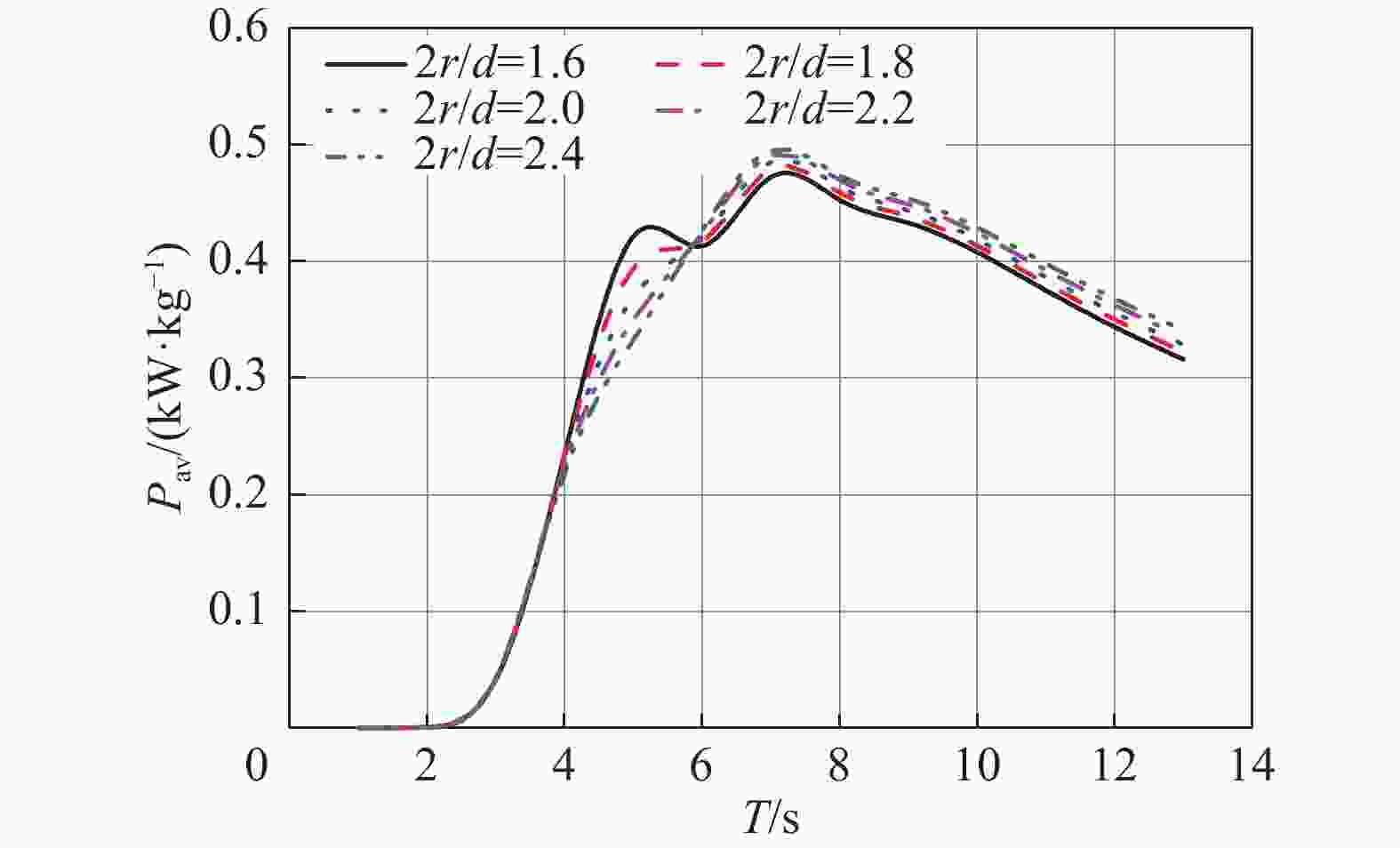
图6反映了不同2r/d下波能浮子阵列的功率体积比Pav随周期的变化关系。由图可知,在2~4 s范围内,浮子的功率体积比基本一致,在4~6 s范围内,浮子的功率体积比随着2r/d的增大而减小,6 s之后则随着浮子的2r/d的增大而增大,因此说明在不同的周期范围内浮子的功率体积比变化趋势是不同的。因此在对不同的海域下,浮子的外形尺寸优化时,需要综合考虑浮子的发电性能和经济性。
-
计算目标海况下的年总发电功率,引入年总波浪功率Ptotal(year)和年单位体积比Pav(year)用来评估风电场海域内波能浮子的能量捕获性能:
$$ {P}_{{\rm{total}}\left({\rm{year}}\right)}={{\sum }_{j=1}^{M}{\left(\frac{{H}_{j}}{2}\right)}^{2}}\times {P_{{\rm{total}}}}\left({T}_{j}\right)\times {{S}_{j}} $$ (9) $$ {P}_{{\rm{av}}\left({\rm{year}}\right)}=\frac{{P}_{{\rm{total}}\left({\rm{year}}\right)}}{\rho {V}_{{\rm{total}}}} $$ (10) 式中:
Sj ——不同周期、波高情况下的联合概率分布;
Hj ——波高分布(m);
Tj ——周期分布(s);
Ρ ——海水密度(kg/m3),取1 025 kg/m3。
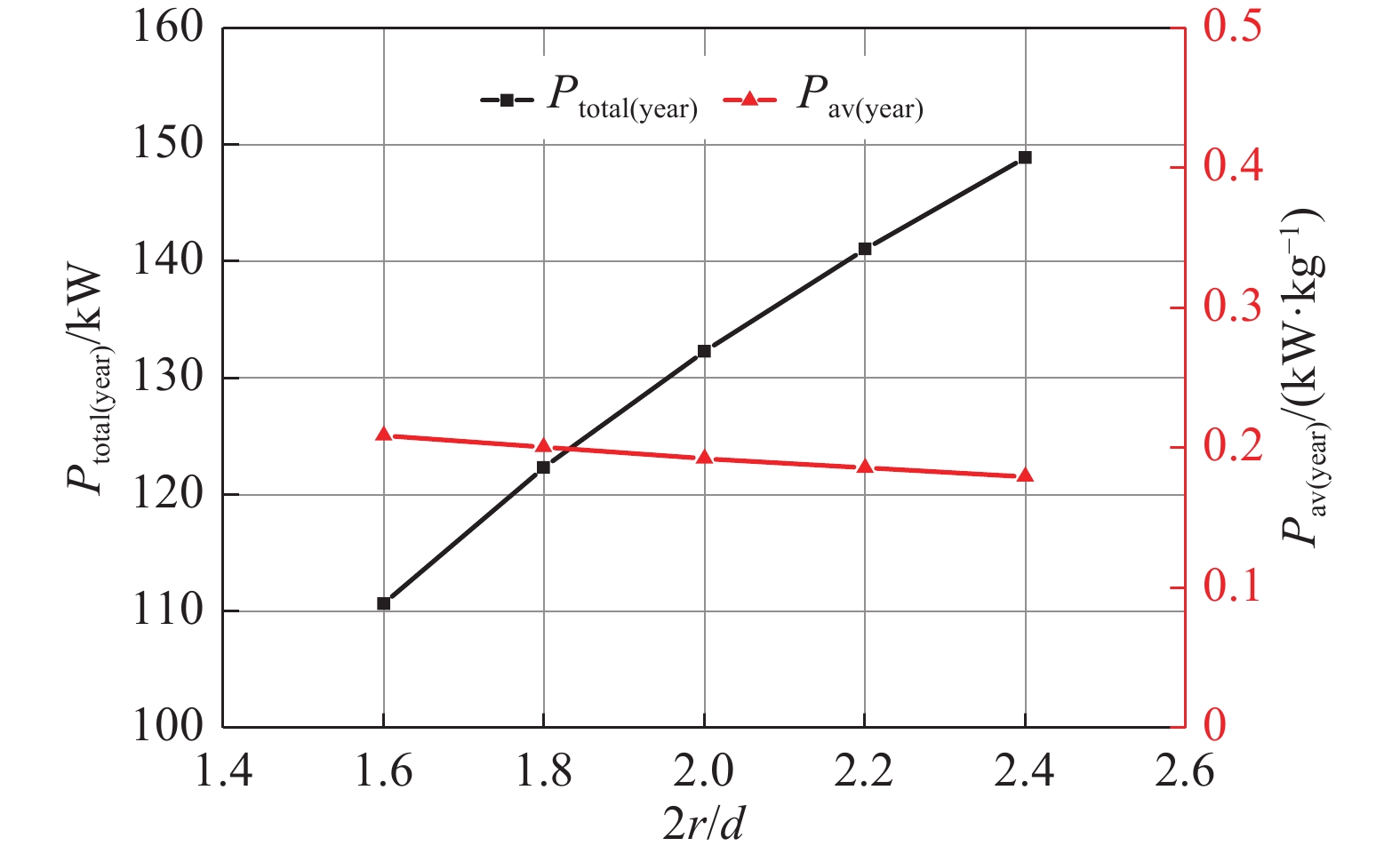
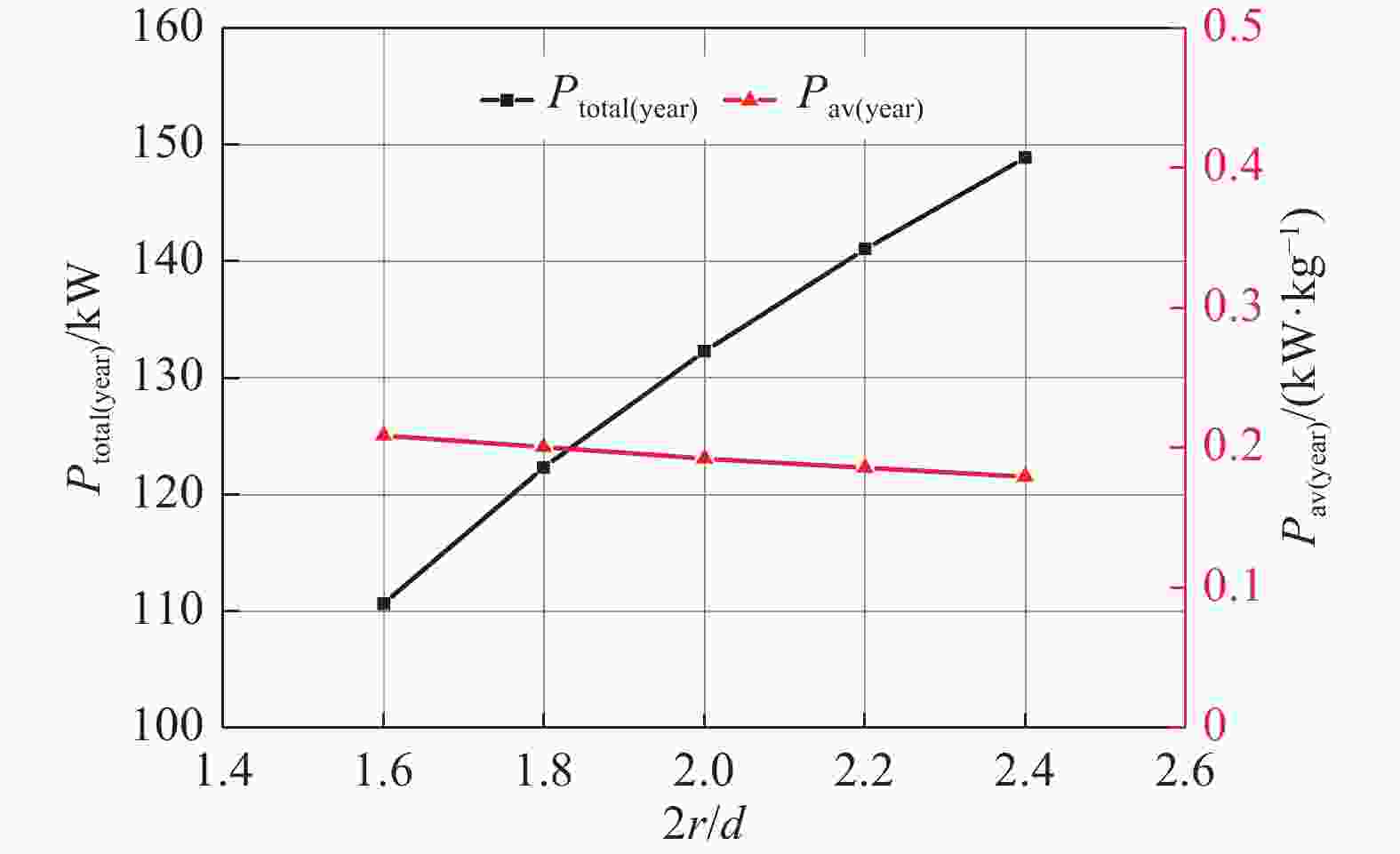
图7反映了风电场海域海况下波能浮子阵列年总发电功率Ptotal(year)和年单位体积比Pav(year)随2r/d变化关系。由图可知,风电场海域海况下波能阵列年总发电功率Ptotal(year)随着2r/d增大而逐渐增加,而年单位体积比Pav(year)变化较小,说明在不同2r/d的波能阵列之间造价的差异非常小。说明考虑到波能浮子阵列-平台系统的发电性能和经济效益,应选用2r/d更大的WEC与平台相结合。
-
因为波能浮子主要在固有周期附近工作,对波能浮子阵列的总发电功率有很大影响,因此考虑改变波能阵列的固有周期Tp,探索适合风电场海域的波能浮子固有周期。通过公式(4)分别计算共振周期Tp=3.50 s,4.00 s,4.50 s和4.69 s的浮子半径r,吃水d,并按布置原则布置。通过前面的验证发现直径吃水比2r/d越大波能阵列的发电功率越高,因此选择浮子数N=6的阵列中波能浮子2r/d较大的4组进行研究。探究不同固有周期Tp的波能阵列在风电场海域海况的年总发电功率Ptotal(year)和年单位体积比Pav(year)。表3列出来不同共振周期Tp下,波能浮子阵列相关性能参数。2r/d越大,则说明浮子越扁平。
Tp/s 2r/d r/m d/m Ptotal(year)/kW Pav(year)/[W·(kg)−1] 3.5 4.0 3.09 1.54 145.9 51% 4.5 3.30 1.47 157.8 51% 5.0 3.50 1.40 168.3 51% 5.5 3.67 1.34 176.7 51% 4.0 3.2 3.54 2.21 216.3 40% 3.4 3.67 2.16 221.6 39% 3.5 3.73 2.13 223.8 39% 3.6 3.80 2.11 226.3 38% 4.5 1.8 3.05 3.39 122.3 20% 2.0 3.29 3.29 132.3 19% 2.2 3.51 3.19 141.1 19% 2.4 3.72 3.10 148.9 18% 4.7 1.4 2.75 3.94 108.3 19% 1.6 3.04 3.80 112.6 17% 1.8 3.31 3.68 127.6 16% 2.0 3.57 3.57 131.7 15% Table 3. Performance parameters of WEC array in sea conditions
由表可知,同一固有周期下,波能浮子阵列的年总发电功率Ptotal(year)随着2r/d的增大而增大,但年单位体积比Pav(year)变化较小。对比不同固有周期下,固有周期Tp越小,浮子的2r/d越大,浮子越扁平,相对的浮子的功率体积比也越大,即浮子的经济性越好。而波能浮子阵列的功率输出则是随着固有周期Tp的增大,先增大后减小,即在Tp=4.0 s时的年总发电功率Ptotal(year) 明显大于其他固有周期。综合考虑波能浮子的发电功率和经济性,Tp=4.0 s时总发电功率Ptotal(year) 最大达226 kW,明显大于其他固有周期,同时相比于Tp=3.5 s时,Ptotal(year)增加了约30%,而Pav(year)减小了约10%,故收益增加大于成本增加。综上,该风电场海域海况下Tp=4.0 s时波能阵列固有周期最优。
-
通过对波能浮子阵列的浮子外形尺寸的优化和固有周期的分析对比,得出以下结论:
1)同一固有周期下,波能浮子越扁平,发电功率越大,且功率体积比变化很小。这说明在某一确定的固有周期下,选择越扁平的波能浮子,波能阵列的功率输出越大,且经济性相近。
2)对于某一固定的海况,可以通过对波能浮子的固有周期进行优化,来获得更大的功率输出。但浮子的经济性会随着固有周期Tp的增大而降低,因此在考虑波能浮子与海上风电融合项目时,应综合考虑功率输出和经济性两方面,并根据对应海域海况对波能浮子应进行定制化设计。
3)本文中将波能浮子阵列与海上浮式风机平台结合,波能浮子阵列仅相对于平台做垂向运动的单自由度下的能量输出。通过对波能浮子阵列外形尺寸和固有周期进行优化分析,探索在某一固定海况下的波能浮子阵列最优的功率输出,同时考虑了波能浮子阵列的经济性。希望对波浪能与海上风机的融合发展提供一些新想法。
Power Optimization of Wave Energy Converter (WEC) Arrray Based on Sea Conditions of a Wind Farm
doi: 10.16516/j.gedi.issn2095-8676.2023.01.018
- Received Date: 2022-04-28
- Rev Recd Date: 2022-09-05
- Available Online: 2022-12-13
- Publish Date: 2023-01-11
-
Key words:
- wind and wave couppling /
- WEC /
- potential flow theory /
- inherent period /
- optimal power
Abstract:
| Citation: | LIU Pin, HAN Ronggui, REN Zhongjin, LÜ Linlin. Power Optimization of Wave Energy Converter (WEC) Arrray Based on Sea Conditions of a Wind Farm[J]. SOUTHERN ENERGY CONSTRUCTION, 2023, 10(1): 139-145. doi: 10.16516/j.gedi.issn2095-8676.2023.01.018 |


















 DownLoad:
DownLoad: