-
近年来工业生产与居民生活对输电需求逐步提高,而现有角钢输电塔已持续运行多年,在原老旧输电塔设备上更换大功率输电设备超过原有输电塔设计荷载要求[1-3];由于沿海地区受热带气旋所引发风灾导致大量输电设备损坏、倒塌[4-6],我国将抗风设计规范提高以适应不同地区建筑抗风设计要求,原有老旧输电塔已不满足设计使用要求[7],将之推倒重建周期长、代价大,因此采用辅助构件对原有角钢输电塔加固成为提高结构承载力行之有效的措施[8-9]。
角钢塔并联加固技术近年来引起国内外学者的广泛关注,祝凯等[10]通过十字填板连接件在原角钢外侧并联加固角钢构成双角钢十字组合截面构件,并通过有限元分析确定了填板厚度、角钢壁厚、长细比、填板间距等参数对加固结构承载力的影响。苏子威等[11]通过十字填板与角形夹具将副主材角钢并联在原角钢外侧形成十字形组合截面对角钢进行加固,并对加固后的组合构件进行了轴压试验,确定了夹具数量、布置方式、螺栓预紧力等对构件传力效率和承载力的影响。姚瑶等[9]通过角形填板夹具在原角钢内侧并联同尺寸加固角钢构成组合构件对原结构进行加固,通过轴压试验确定了试件的受力机理、应变变化规律等,并运用数值分析探讨了设计参数对构件承载力的影响。Yang等[10]通过角形夹具并联加固角钢对格构式输电塔塔腿进行加固,提出了用于模拟连接螺栓转动的三维模型,并通过有限元分析验证了三维维螺栓连接模型的通用性和关键设计参数对加固构件承载力的影响。
现有研究中角钢输电塔塔腿加固多采用并联加固角钢构成十字组合截面的方式[11-13],但外部并联同尺寸角钢增大了构件的迎风面积,在受风灾影响严重区域其加固效果远不如预期,因此在不过分增大原有迎风面积的前提下,本文提出在角钢肢外侧并联加固槽钢构成组合截面的加固方式。
-
被加固角钢尺寸为L140×10,通过单轴拉伸试验确定钢材的屈服强度、抗拉强度与弹性模量等参数,如表1所示。
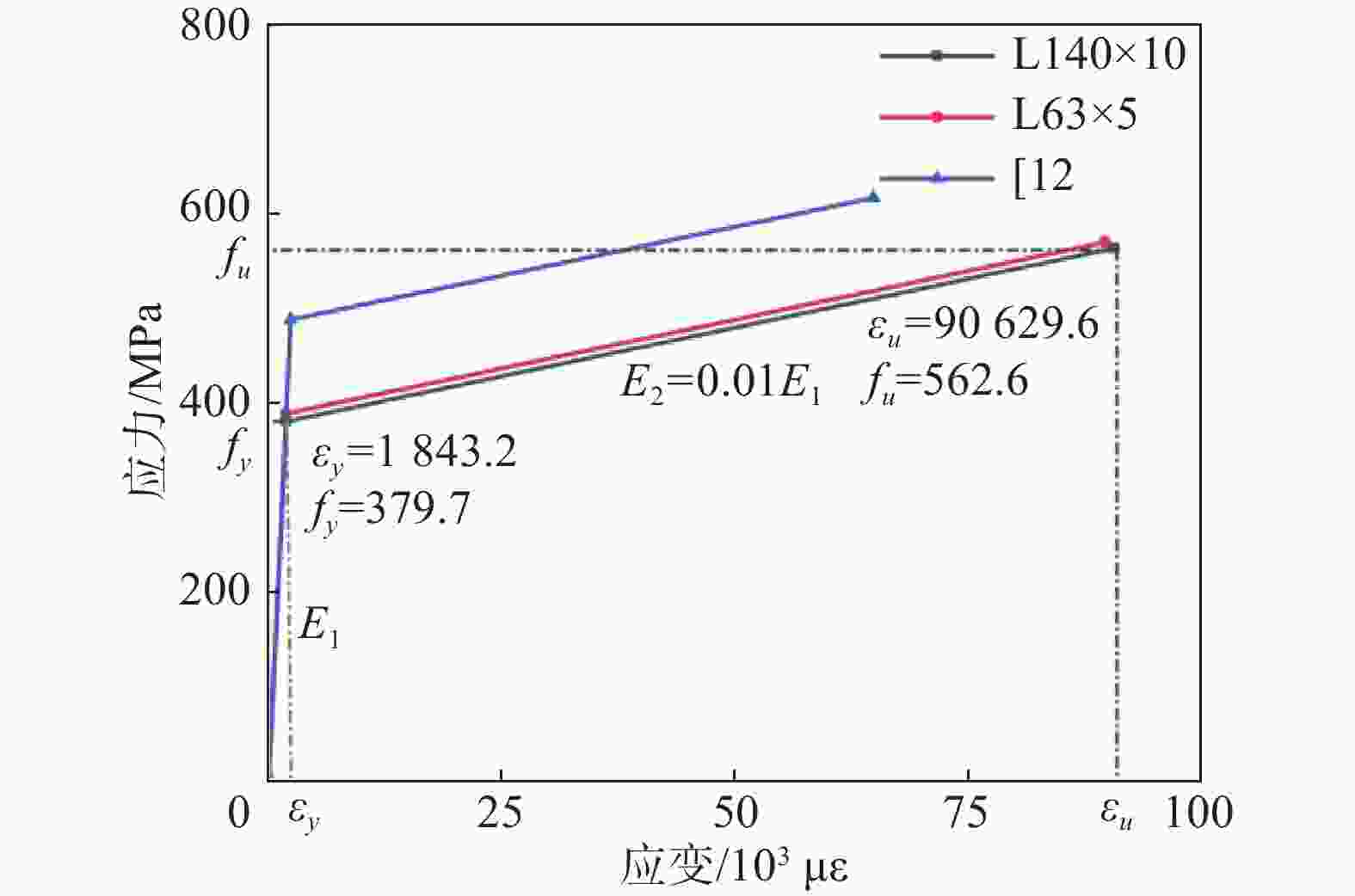
试件类别 弹性模量/MPa 屈服强度/MPa 抗拉强度/MPa L140×10(角钢) 2.06×105 379.70 562.60 L63×5(角钢) 2.06×105 388.48 569.23 [12(槽钢) 2.06×105 487.32 615.92 Table 1. Steel performance parameter
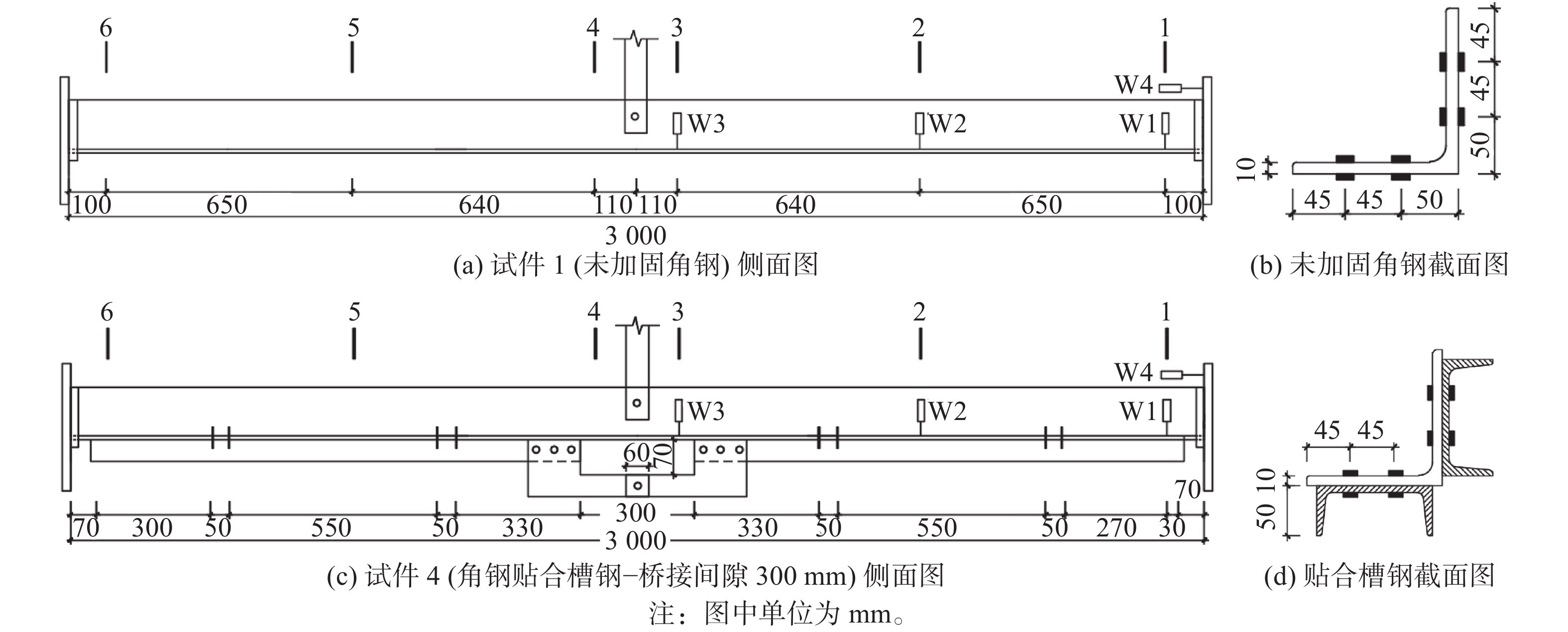
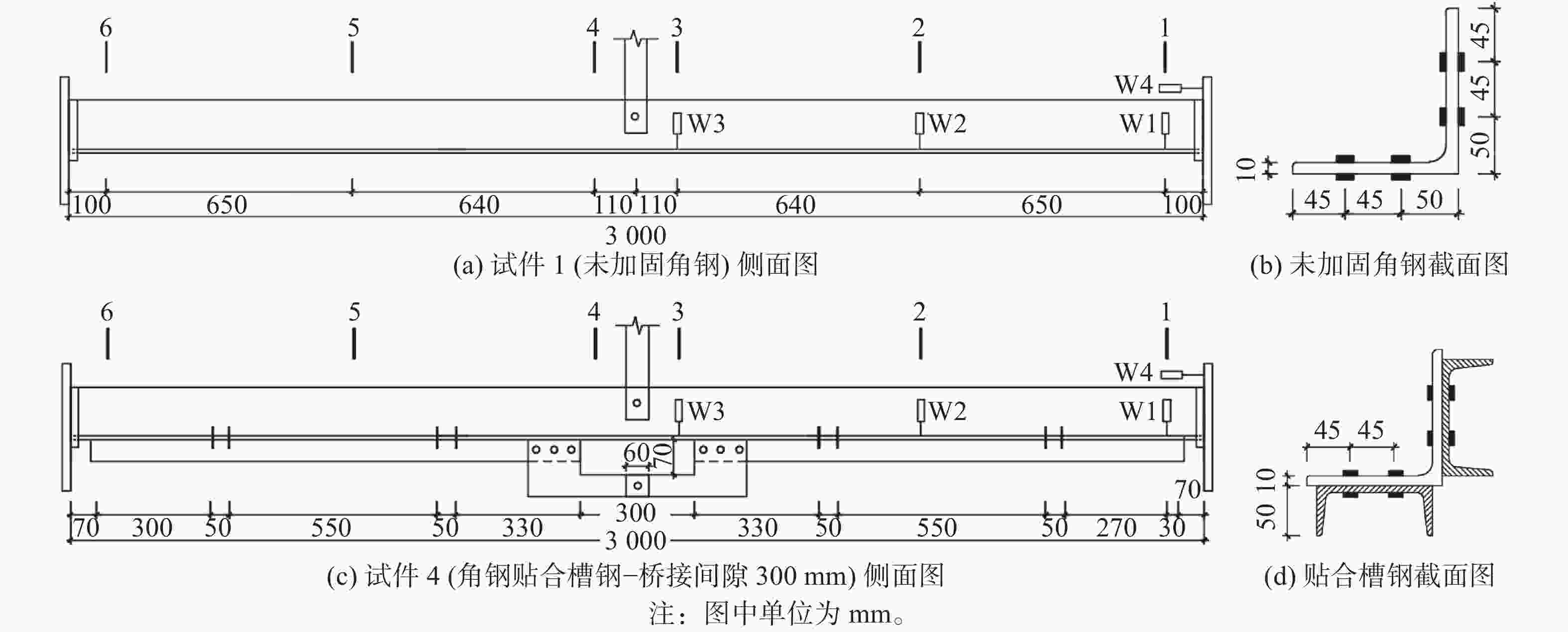
本试验试件共分两组:试件1为未加固角钢试件,计3根试样;试件4为本文拟提出的贴合槽钢加固方案,计3根试样。试件1中单角钢长度为3 m,试件中部两侧对称设置侧向支撑模拟角钢输电塔实际杆系受力机制,单角钢与侧向支撑间采用螺栓连接,如图1(a)所示;试件4为角钢贴合槽钢试件,被加固角钢(单角钢)两肋通过螺栓连接槽钢,两者通过螺栓预紧力固定,侧向支撑两侧贴合槽钢通过桥接板连接,桥接间距为300 mm,如图1(c)所示。为便于轴向加载,被加固角钢上、下端设有边长为300 mm、厚度为40 mm的方形加载板。
-
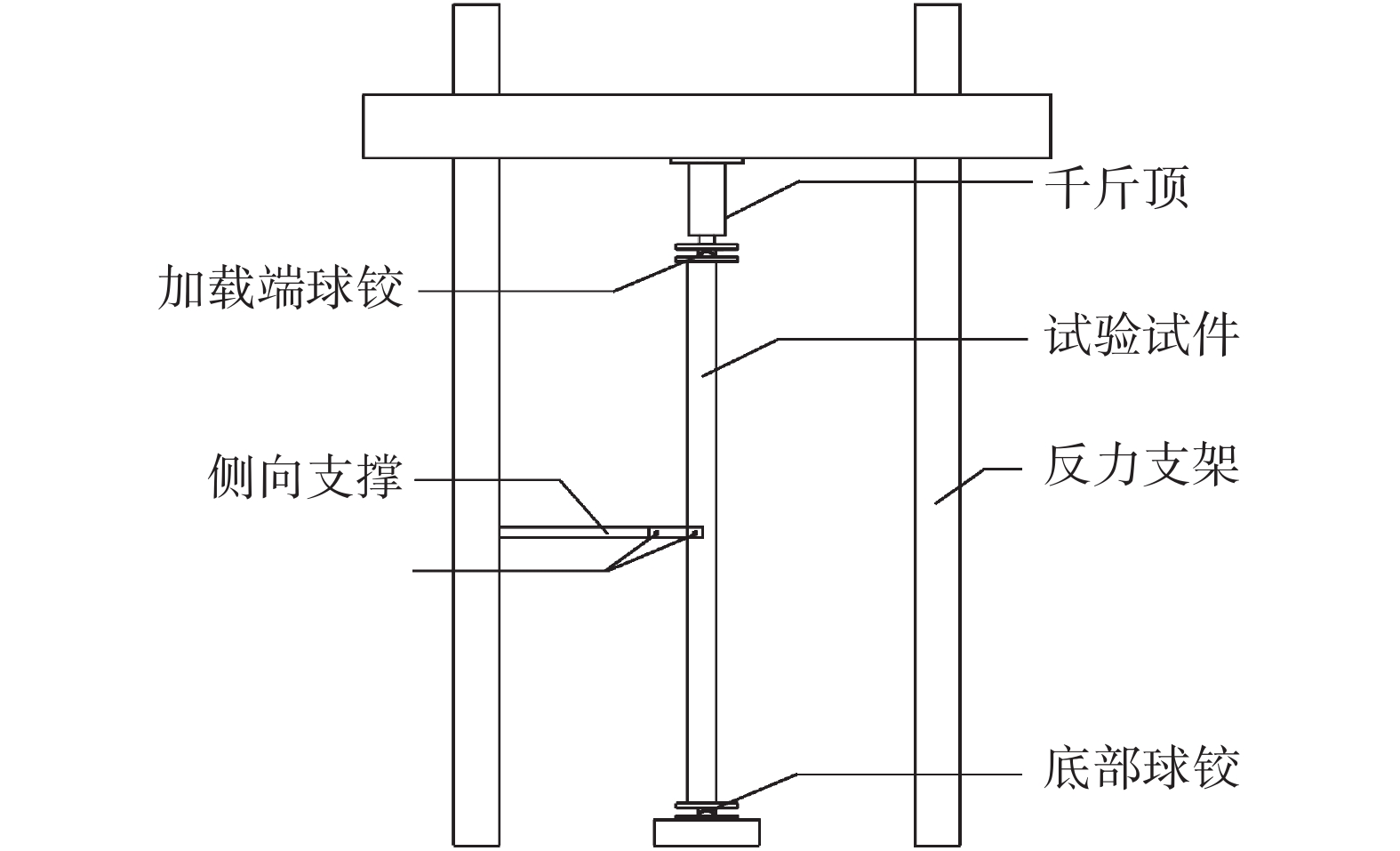
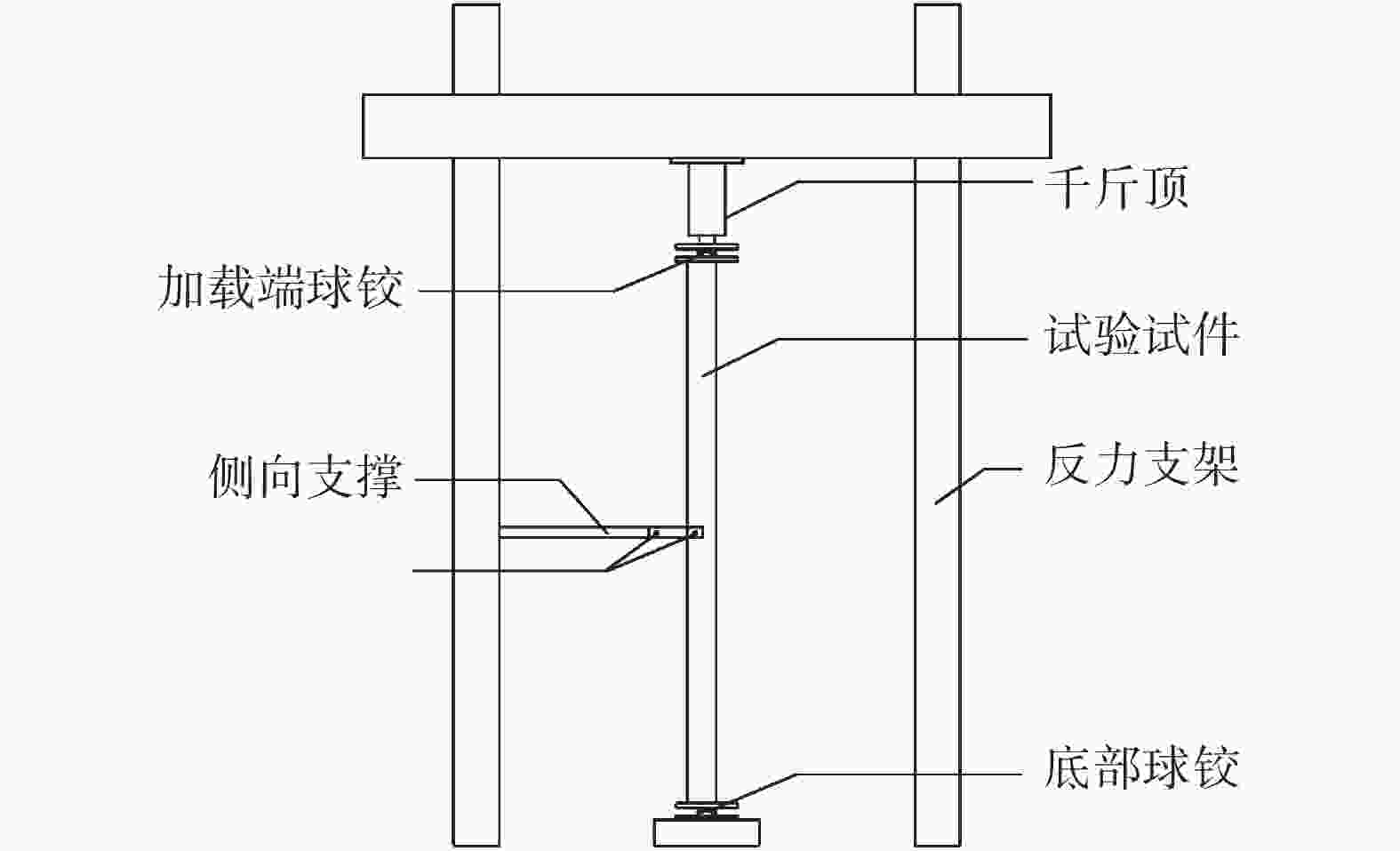
本文试验采用500 t液压伺服机控制千斤顶加载,角钢长边方向与反力架长边方向平行,铰接端与加载端处连接构造采用球型铰;为满足外侧贴合槽钢不与端板相接触,二者间距设置为70 mm,以避免加固材直接承力;侧向支撑对称设置于被加固角钢中点两侧,二者间采用螺栓连接,使被加固角钢与侧向支撑间可发生转动;侧向支撑与反力支架连接梁间采用螺栓连接,如图2所示。
-
试验采用四阶段加载:第一阶段为预加载,采用1 kN/s的速度加载至50 kN并持荷15 s,以消除试验装置间隙,确保加载装置与试件充分接触;第二阶段为轴压力控制加载,每20 kN为单位加载步,当轴压荷载值达到500 kN时持荷15 s;第三阶段采用位移控制加载,每0.2 mm为单位加载步;当轴压荷载临近850 kN时,减半加载步,采用0.1 mm为单位加载步,直至构件到达极限承载力,当轴压荷载下降至峰值荷载的85%时停止试验。
-
位移计沿试件长度方向依次顺序布置,加载端沿轴向布置W1,自加载端至侧向支撑沿横向依次布置3个位移计:W2、W3、W4,如图1(a)所示;为准确量测轴力作用下试件1和试件4的应力分布,分别沿试件长度方向的1~6截面设置应变测点,如图1(a)、图1(c)所示,试件1和试件4截面应变测定布置如图1(b)、图1(d)所示。
-
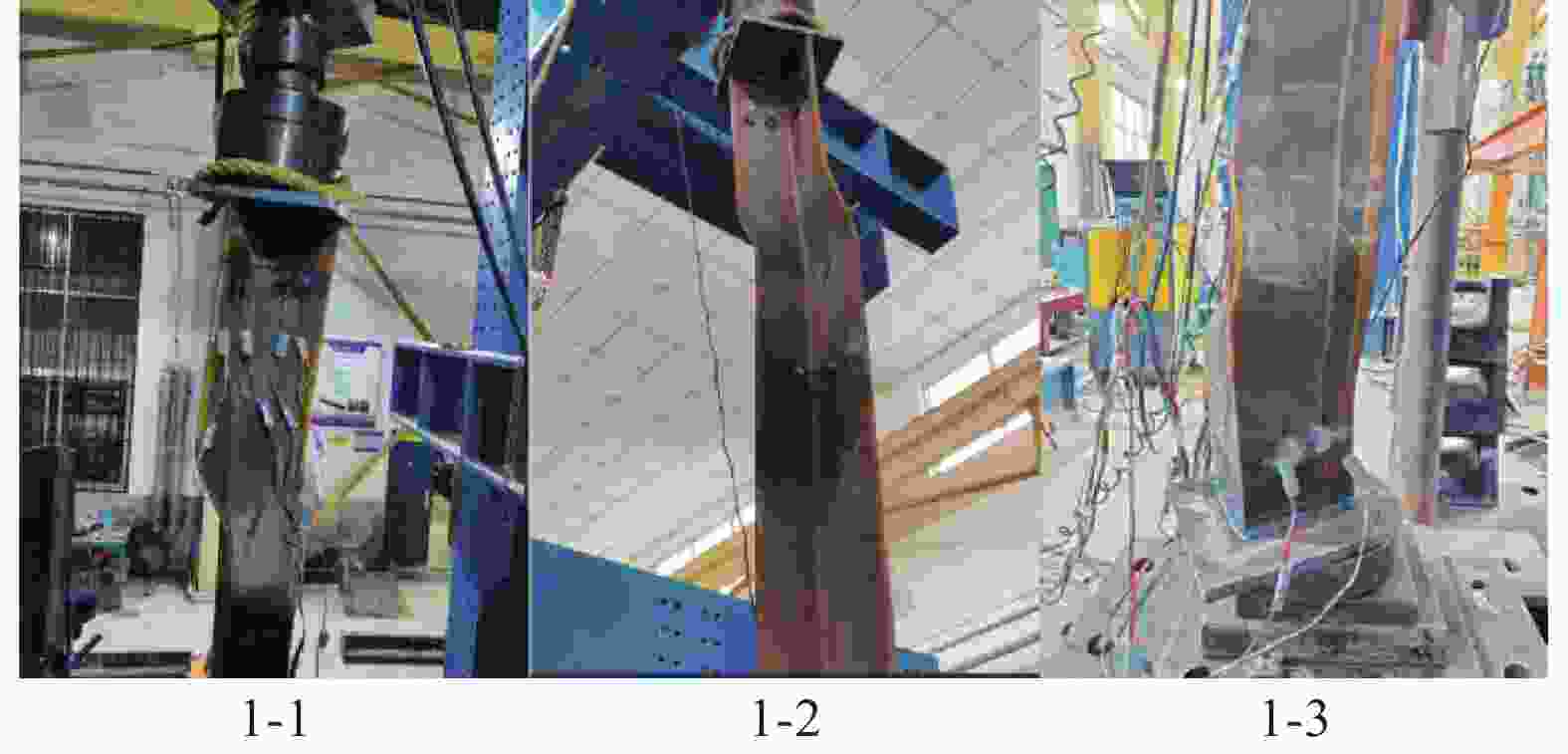
在轴压荷载作用下,未加固角钢失稳发生于四分点与上(下)端中点截面,角钢出现绕弱轴的整体弯曲变形并伴随截面扭转,呈现既弯又扭的失稳形式;角钢发生失稳破坏时端部球铰支座出现明显的转动现象,失稳位置处构件的侧向变形明显,角钢两肢扭转方向一致,试件1的3根同工况试样的破坏现象如图3所示。
-
在轴压荷载作用下,试件4于加载端部发生局部屈曲,主材角钢在轴压荷载作用下出现波浪形屈曲变形,随着轴压荷载不断增大,试件呈现较好的延性,当轴压荷载临近屈曲临界荷载时,随着试件变形增大,荷载-位移曲线呈现陡降趋势,得到了明显的下降段曲线,加载端球铰支座因主材发生显著的局部屈曲变形而出现明显的倾斜,加载过程中3根试样均未出现整体失稳,试件4的3根同工况试样的破坏现象如图4所示。
-
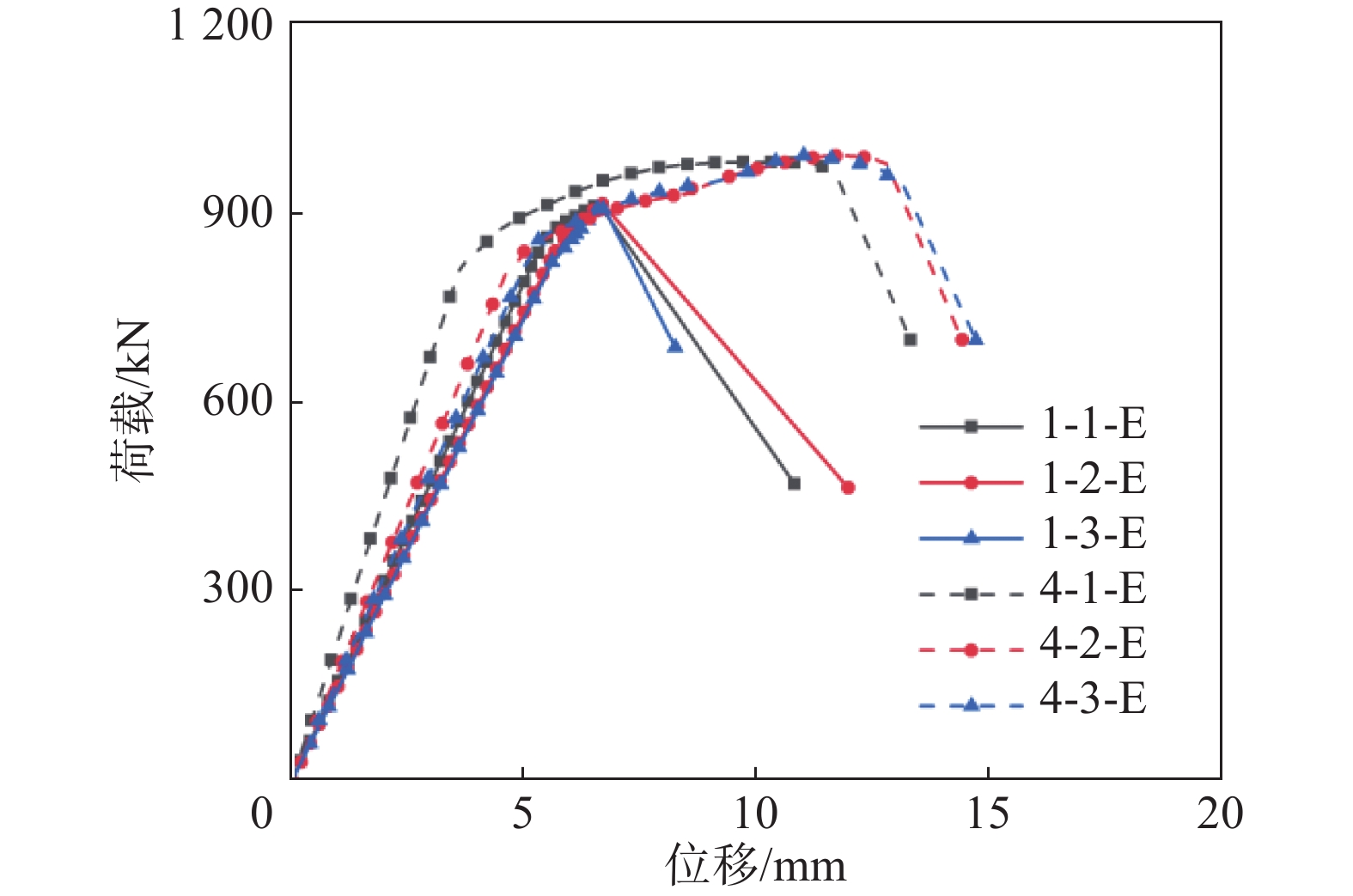
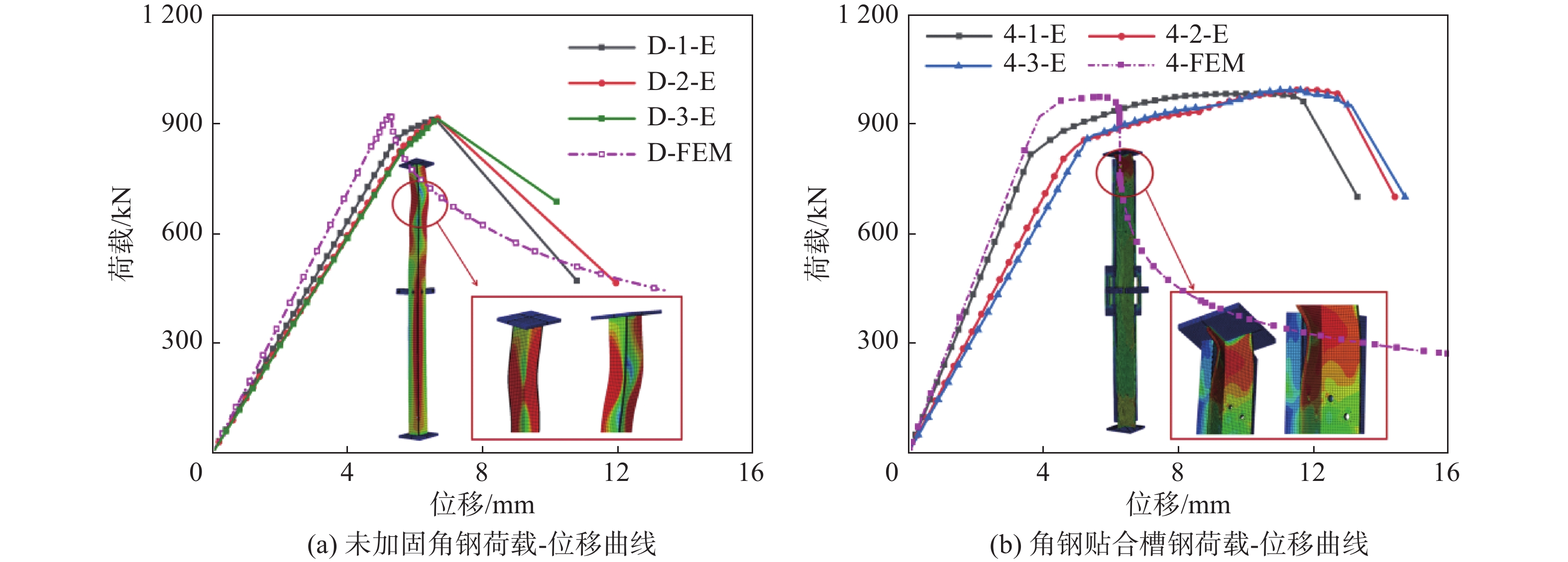
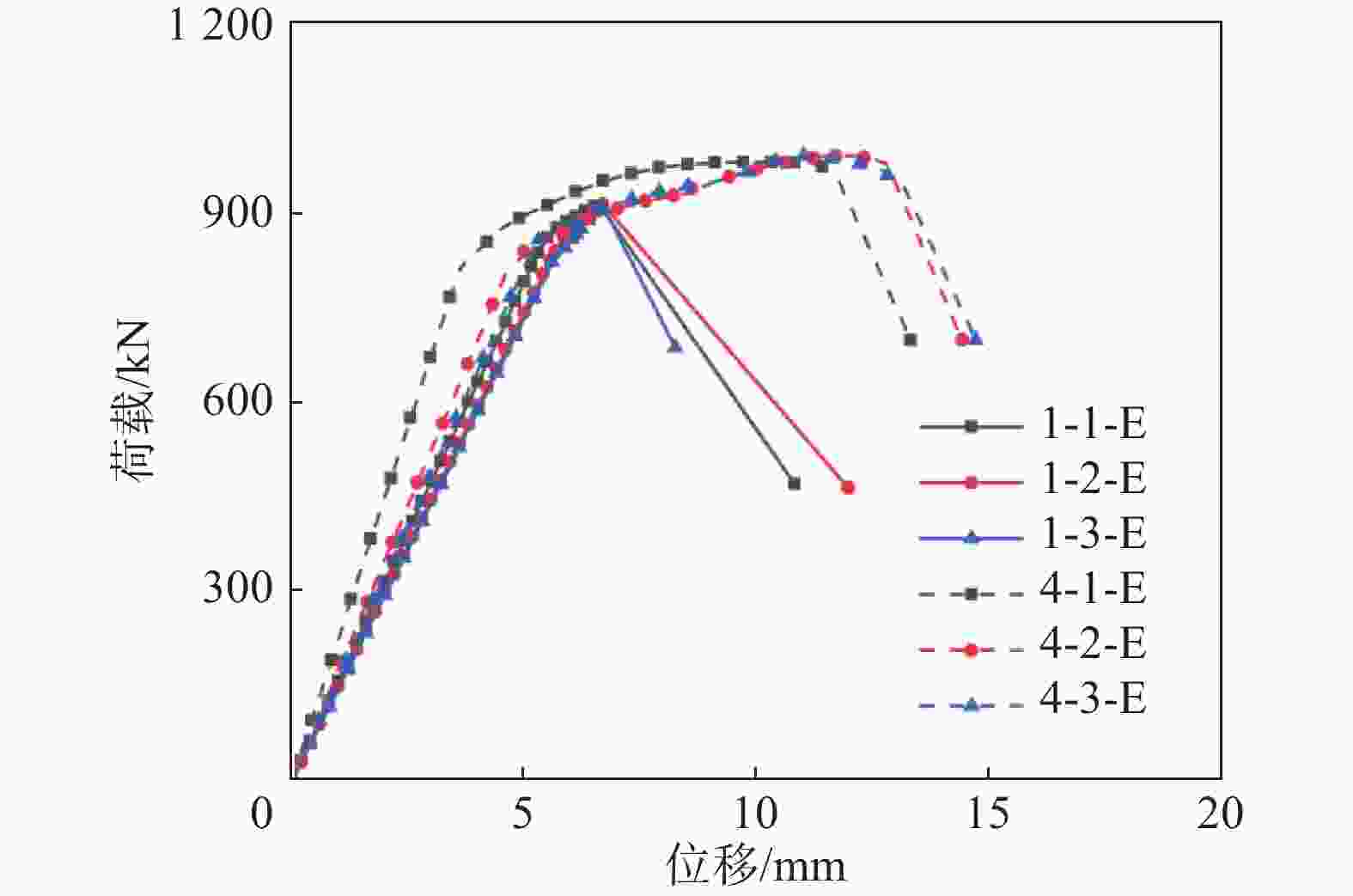
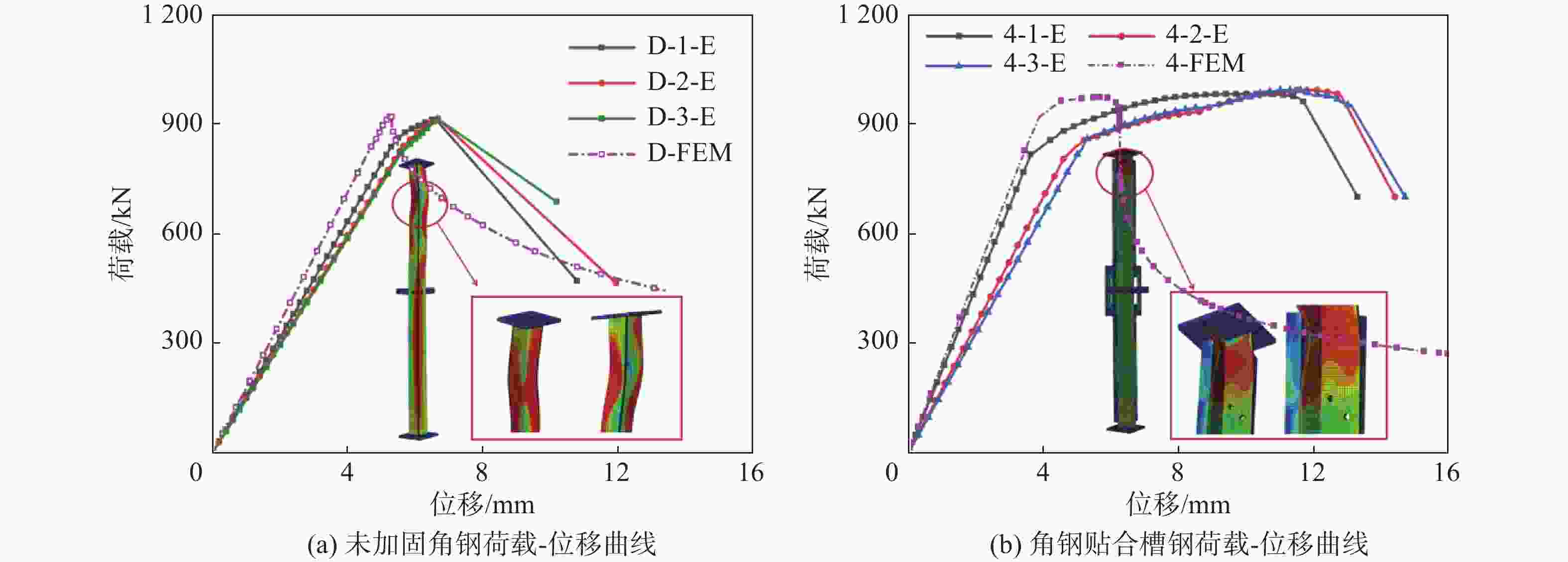
通过实测未加固角钢试件(单角钢)、角钢贴合槽钢试件轴压承载力,可得各试件的荷载-位移曲线如图5所示。
由图5可知,试件1的3根同工况试样的荷载-位移曲线弹性段刚度基本相同,荷载-位移曲线未出现明显的非线性特征,当轴压荷载到达峰值荷载后,承载力迅速下降;试件4的3根同工况试样的荷载-位移曲线弹性段刚度基本相同,且弹性段刚度略大于试件1,荷载位移-位移曲线临近峰值荷载时呈现明显的非线性,轴压荷载增长速度缓慢,轴向变形发展较快,试件4在承载力降低前具有良好的变形性能,当构件变形发展过大已无法继续承载时,承载力迅速下降。角钢贴合槽钢平均峰值承载力为978.60 kN,对比未加固角钢提高6.87%。
通过试件1和试件4的荷载-位移曲线所得峰值承载力与峰值荷载对应轴向位移可知,角钢贴合槽钢试件可有效提高主材角钢轴压承载力,同时可明显改善主材角钢的延性,使角钢由四分点截面处的弯扭失稳(试件1破坏现象)转变为角钢端部的局部屈曲(试件4破坏现象)。
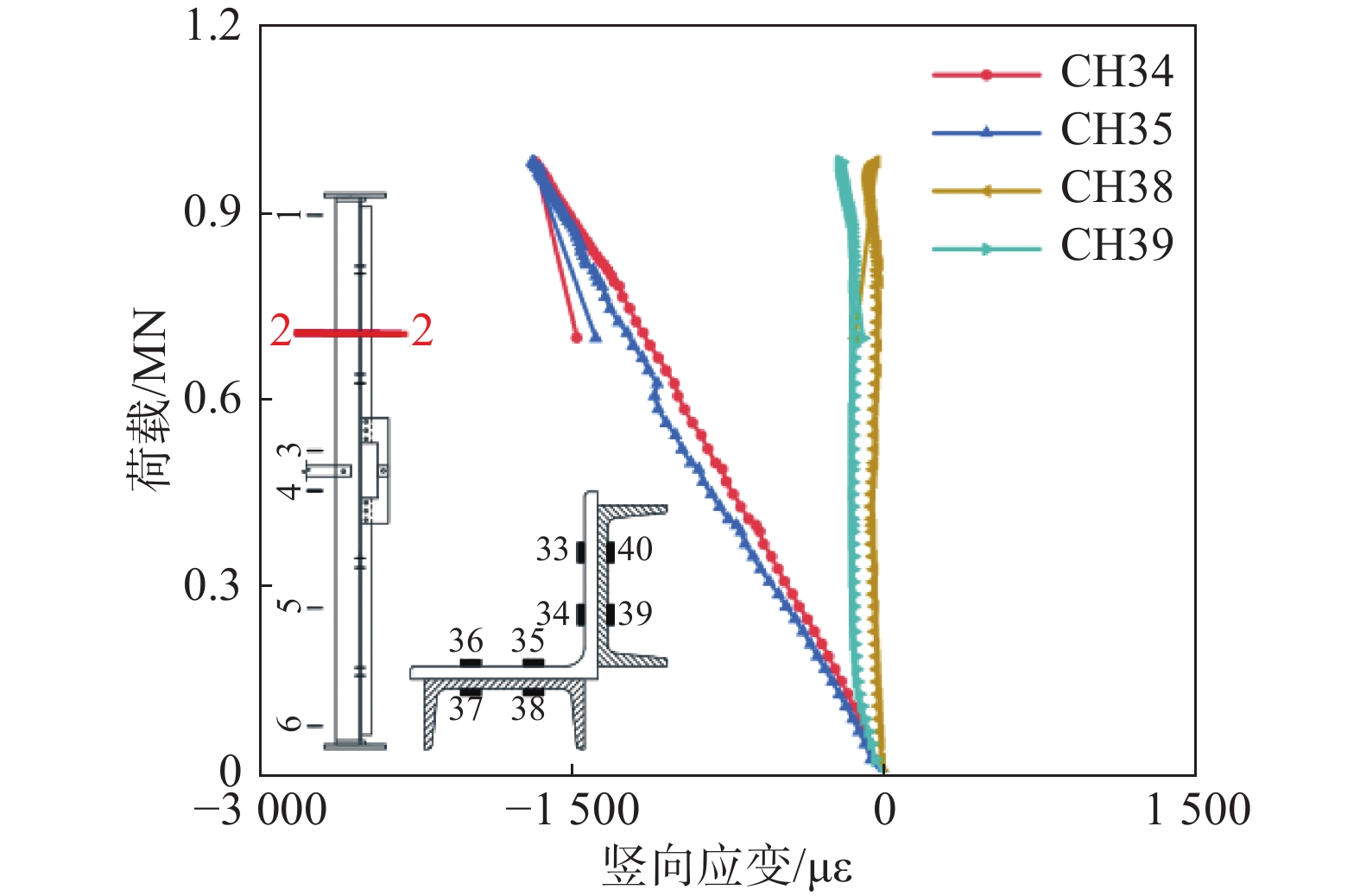
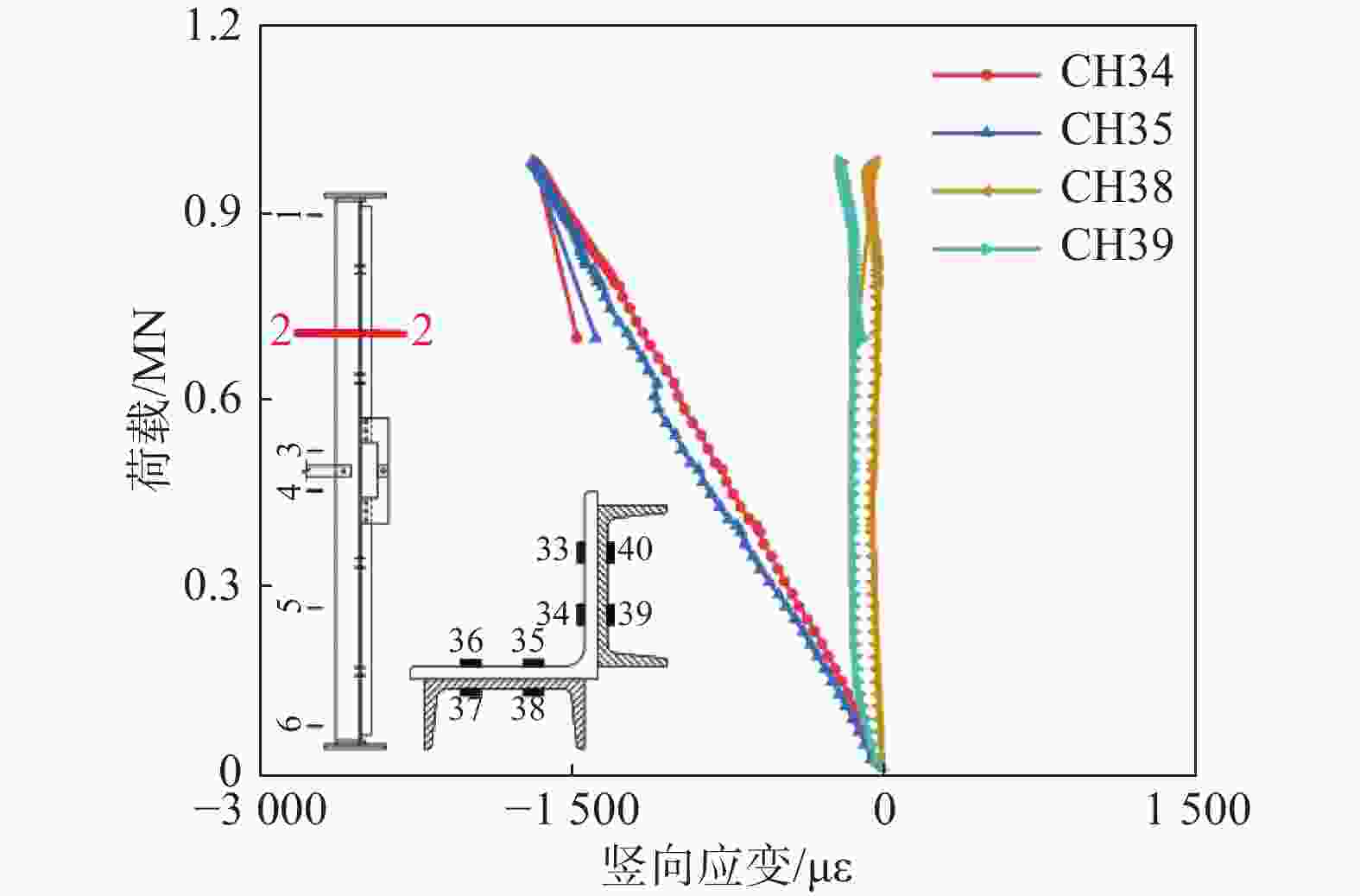
图6所示为试件4的2-2截面(CH34、CH35、CH38和CH39)荷载-竖向应变曲线,由此可知,随着轴压荷载增大,主材角钢测点压应变始终呈增大趋势,贴合槽钢测点在加载初期竖向应变保持不变,当轴压荷载达800 kN时,贴合槽钢压应变呈增大趋势,在临近峰值荷载时协同主材受力。
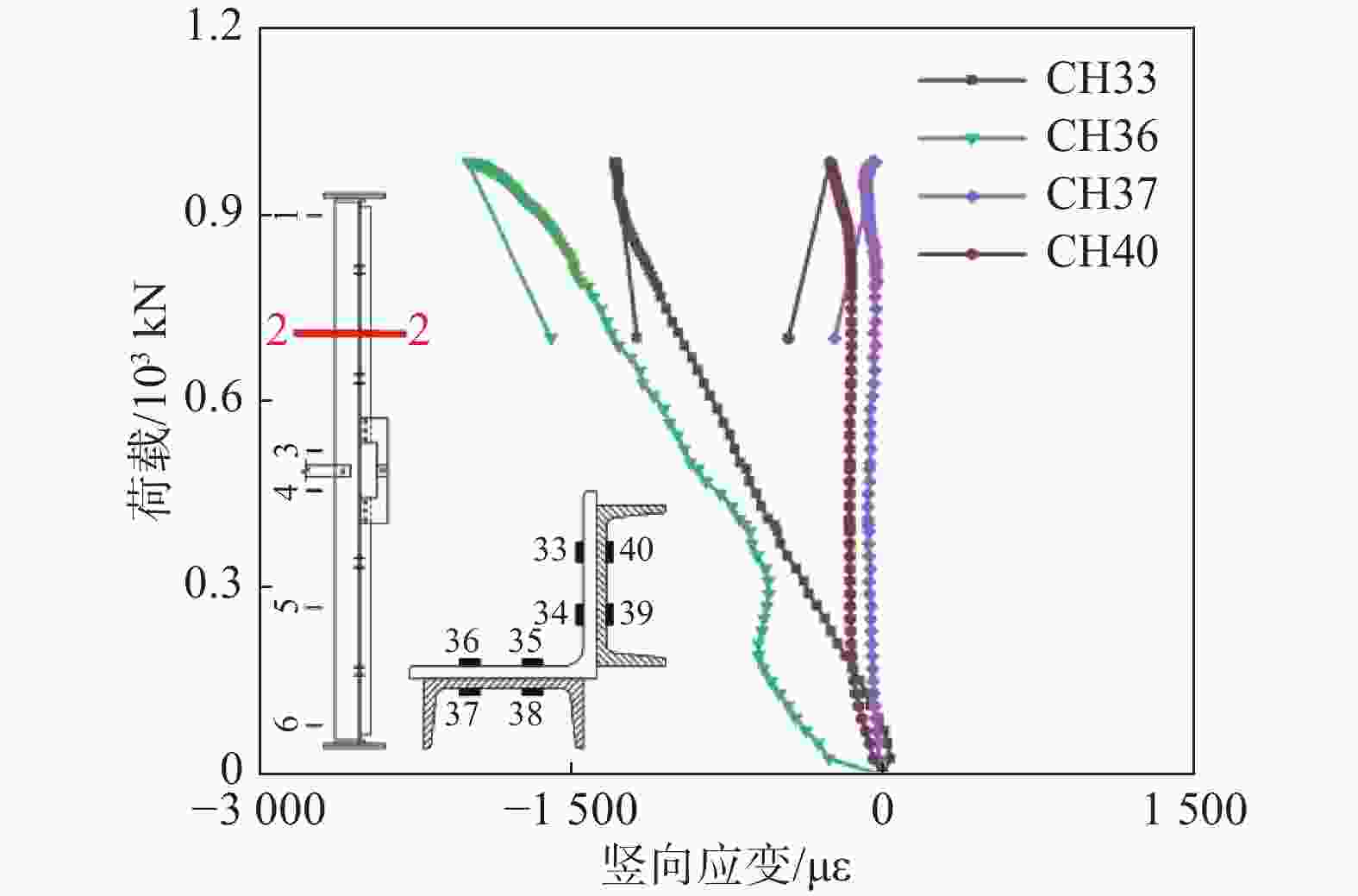
图7所示为试件4的2-2截面(CH33、CH36、CH37和CH40)荷载-竖向应变曲线,由此可知,随着轴压荷载增大,主材角钢测点压应变始终呈增大趋势,因加载初期螺栓与试件间存在空隙且随轴压力增加逐渐压紧从而导致测点36荷载-应变曲线出现突然增大的刚度变化;贴合槽钢测点在加载初期竖向应变保持不变,当轴压荷载达800 kN时,贴合槽钢压应变呈增大趋势,近肢背处荷载-应变变化规律与近肢尖处保持一致,证明主材角钢受力较为均匀。
综上所述,当轴压荷载达800 kN以上时,贴合槽钢与主材协同受压,截面应力出现重分布现象。角钢外侧贴合槽钢有效增大了构件抗弯、扭转、翘曲刚度,使构件由整体弯扭失稳转变为主材板件的局部稳定问题,根本上改变了构件的破坏形式,同时有效提高了构件的承载力和延性。
-
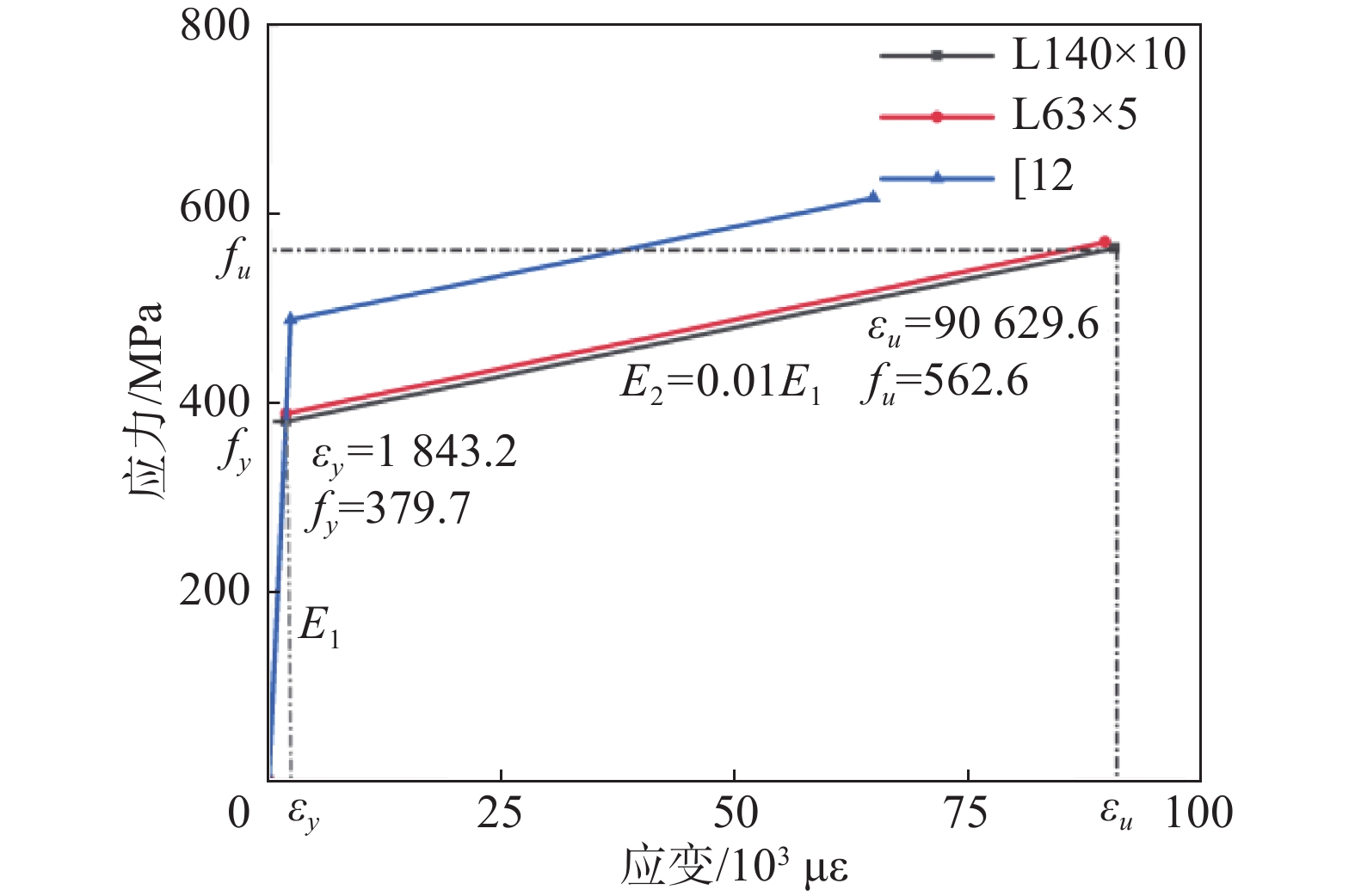
本文采用大型通用有限元软件ABAQUS建立有限元仿真模型,主材角钢与贴合槽钢均采用三维实体线性缩减积分单元C3D8R模拟,采用双折线模型模拟钢材屈服后的应力-应变关系[13],如图8所示。
进行网格划分时采用结构化网格划分技术,将各构件划分为规则的六面体单元,加载端与底部铰支端采用MPC刚性梁耦合参考点施加位移约束,底部采用铰接边界条件,加载端约束x、y方向平动自由度,z方向设置加载位移。侧向支撑端部与反力架连接螺栓外表面设置约束并使侧向支撑可发生绕连接螺栓的有限转动,贴合槽钢与主材角钢间连接螺栓采用MPC刚性梁模拟。采用有限元进行静力分析前导入最低阶屈曲模态作为构件的初始缺陷,导入屈曲模态的比例系数取为L/1000,L为构件长度,各组件间接触关系为硬接触,摩擦系数为0.25。
如图9(a)所示,单角钢有限元模拟所得荷载-位移曲线与试验荷载-位移曲线符合良好,有限元分析所得构件破坏现象与试验保持一致,均为四分点截面处的弯扭失稳;数值模型峰值荷载为921.78 kN,对比试验峰值承载力平均值误差为0.67%。
如图9(b)所示,角钢贴合槽钢有限元模拟所得荷载-位移曲线与试验荷载-位移曲线符合良好,有限元分析所得构件破坏现象与试验保持一致均为端部加载端主材角钢局部屈曲;数值模型峰值荷载为973.10 kN,对比试验峰值承载力平均值误差为0.56%。
-
以未加固角钢、角钢贴合槽钢完整结构有限元模型作为分析基础,分析构件长细比对加固构件承载力的影响,判断角钢贴合槽钢对各长细比构件的加固有效性。
参数化模型信息如下:角钢贴合槽钢构件变长细比分析时始终保持贴合槽钢与角钢端部间距为70 mm,以满足加固材不直接承受轴压荷载的要求,侧向支撑处槽钢断开间距为300 mm,以满足侧向构件安装空间的要求;桥接板长度与试验模型一致为600 mm,角钢与外贴槽钢第一连接螺栓安装位置始终距外贴槽钢端部(铰接段)300 mm,第二连接螺栓安装位置距侧向支撑中截面330 mm,以上参数均不随长细比变化而改变。
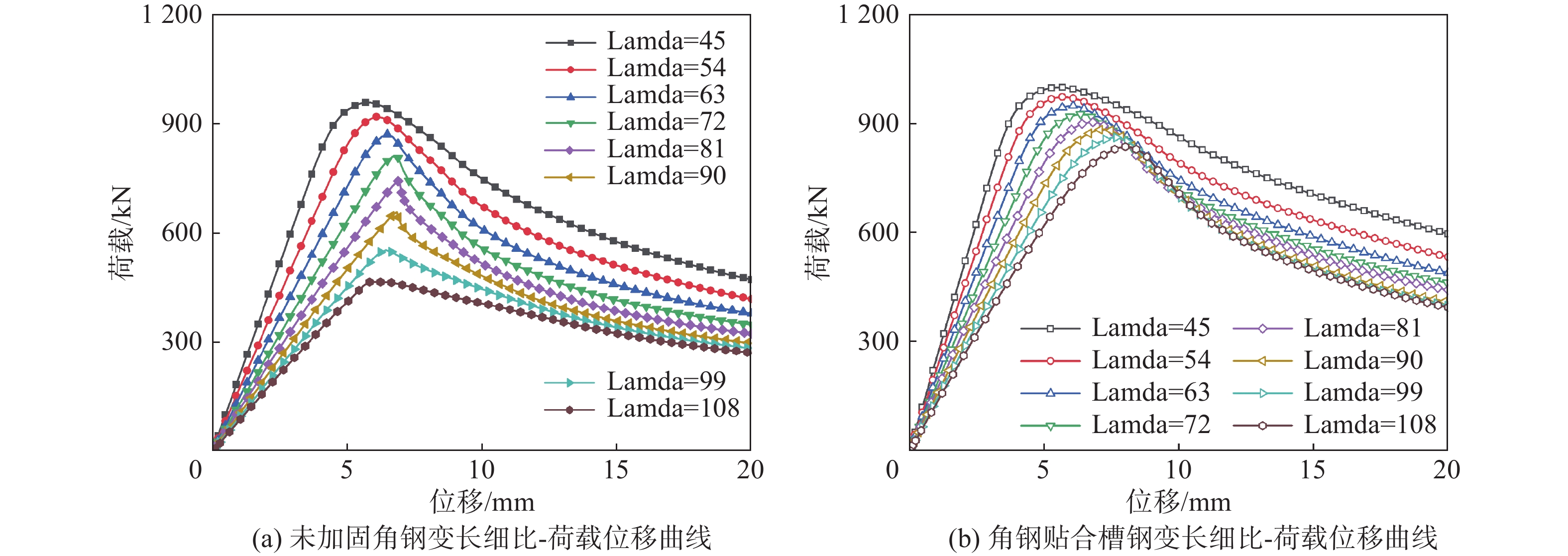
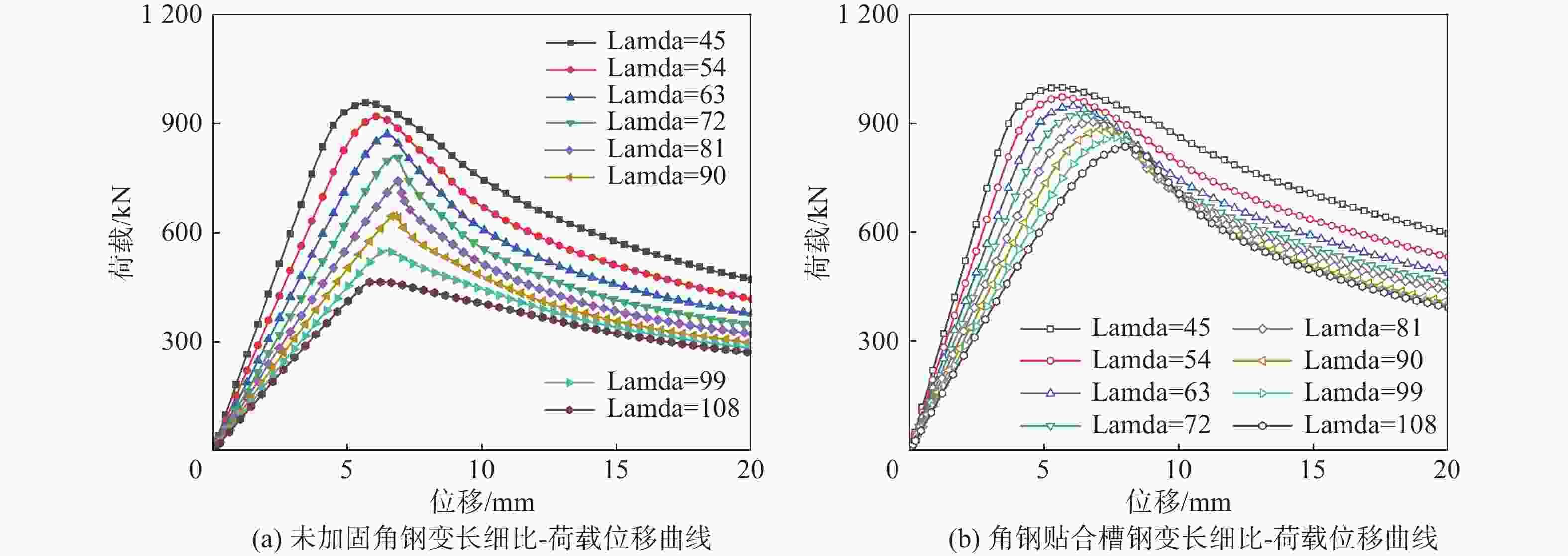
如图10(a)所示,随着构件长细比增大,未加固角钢荷载-位移曲线弹性段刚度随长细比增大而逐渐降低,构件发生由弯扭失稳到弯曲失稳形式的转变;如图10(b)所示,随着构件长细比增大,角钢外贴槽钢荷载-位移曲线弹性段刚度随长细比增大而逐渐降低,刚度下降幅度明显弱于未加固角钢构件,原因在于外贴槽钢与角钢构成组合截面,大幅提高了原有截面的抗弯刚度,使其截面的强弱轴发生转变,构件失效模式由未加固前的弯扭失稳转变为加固后主材角钢的局部屈曲,采用贴合槽钢加固后,长细比增大未能改变加固构件的破坏形式。
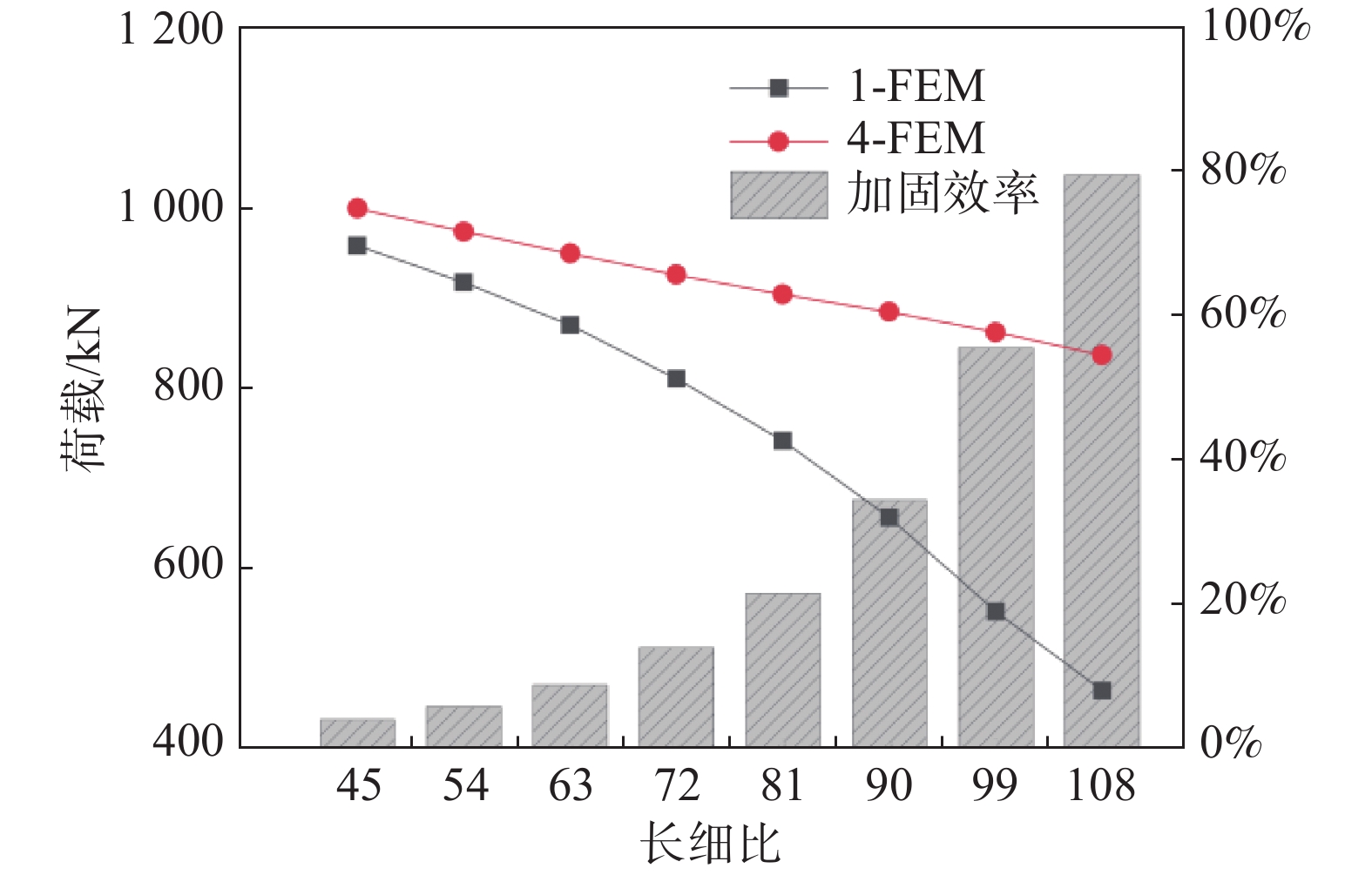
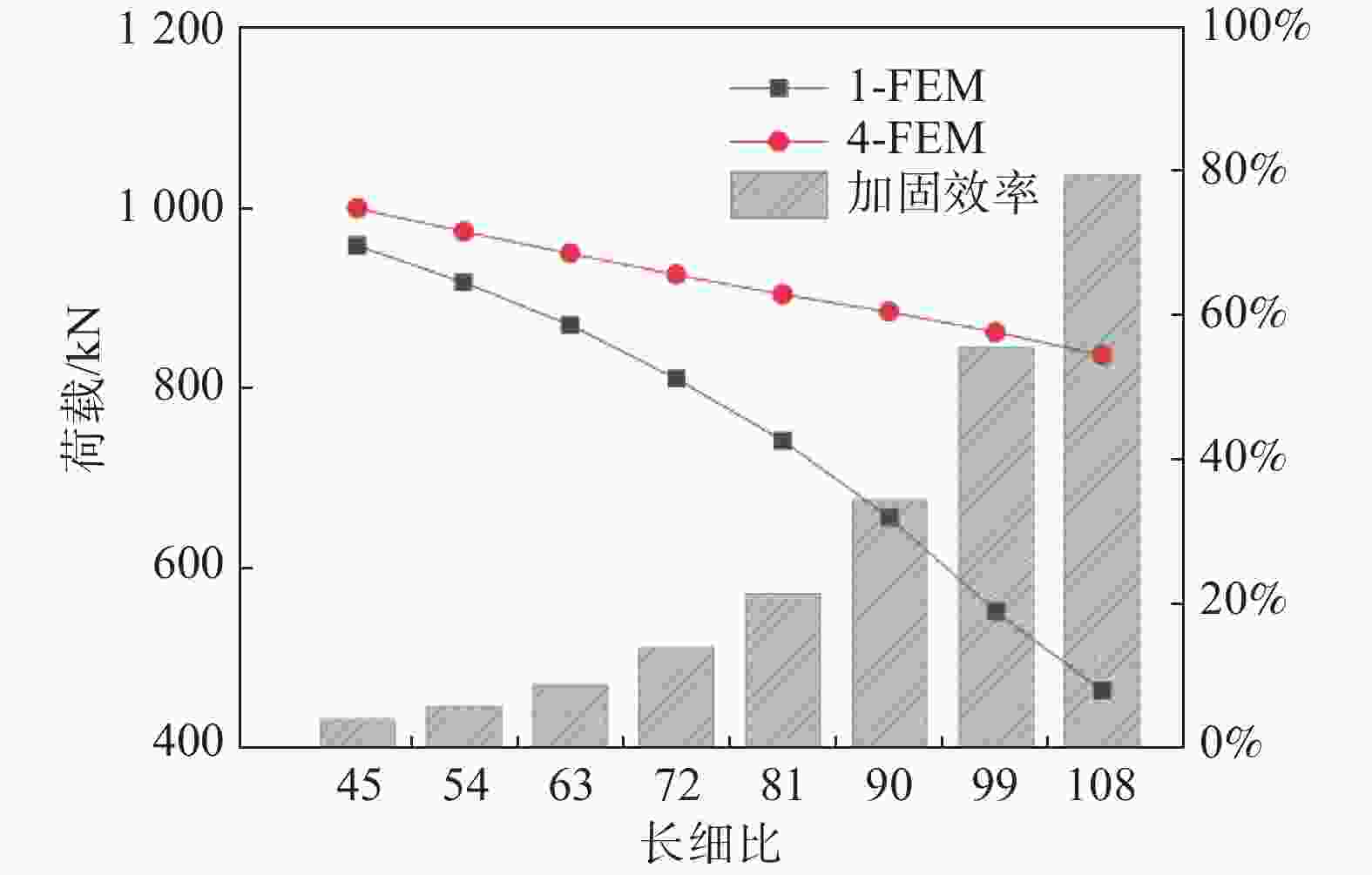
由图11可知,随着角钢长细比增大,角钢贴合槽钢加固效率显著提升。未加固角钢随长细比增大,试件破坏形式由整体弯扭失稳转变为绕截面弱轴的整体弯曲失稳,试件承载力随长细比增大下降迅速;角钢贴合槽钢试件失稳模式随长细比变化不显著,均为加载端部主材角钢的波浪状薄板局部失稳,试件承载力随长细比增大未出现大幅下降趋势,因此采用角钢贴合槽钢所得试件的加固承载力随长细比变化较为可控,可有效提高构件的极限承载力。
-
角钢属于单轴对称构件,当所采用的加固措施对改善角钢弱轴抗弯刚度效果较强时,加固后构件已不易发生整体性的弯扭失稳,转而在主材角钢某一肢发生局部稳定问题[14-15]。
-
根据试件4最终破坏形态,可将加固后构件失稳问题归结为主材角钢局部屈曲,由于所采用的角钢截面宽厚比超限不满足截面局部稳定性要求[16-18],当截面受压时同一截面各测点荷载-应变速率不同,因而截面应力分布并不均匀,角钢肢尖边缘处将会产生明显的集中应力问题,当角钢肢尖截面应力达到屈服,试件将因角钢肢局部屈曲而丧失承载力。
由于角钢翼缘厚度与翼缘幅面宽度之比介于
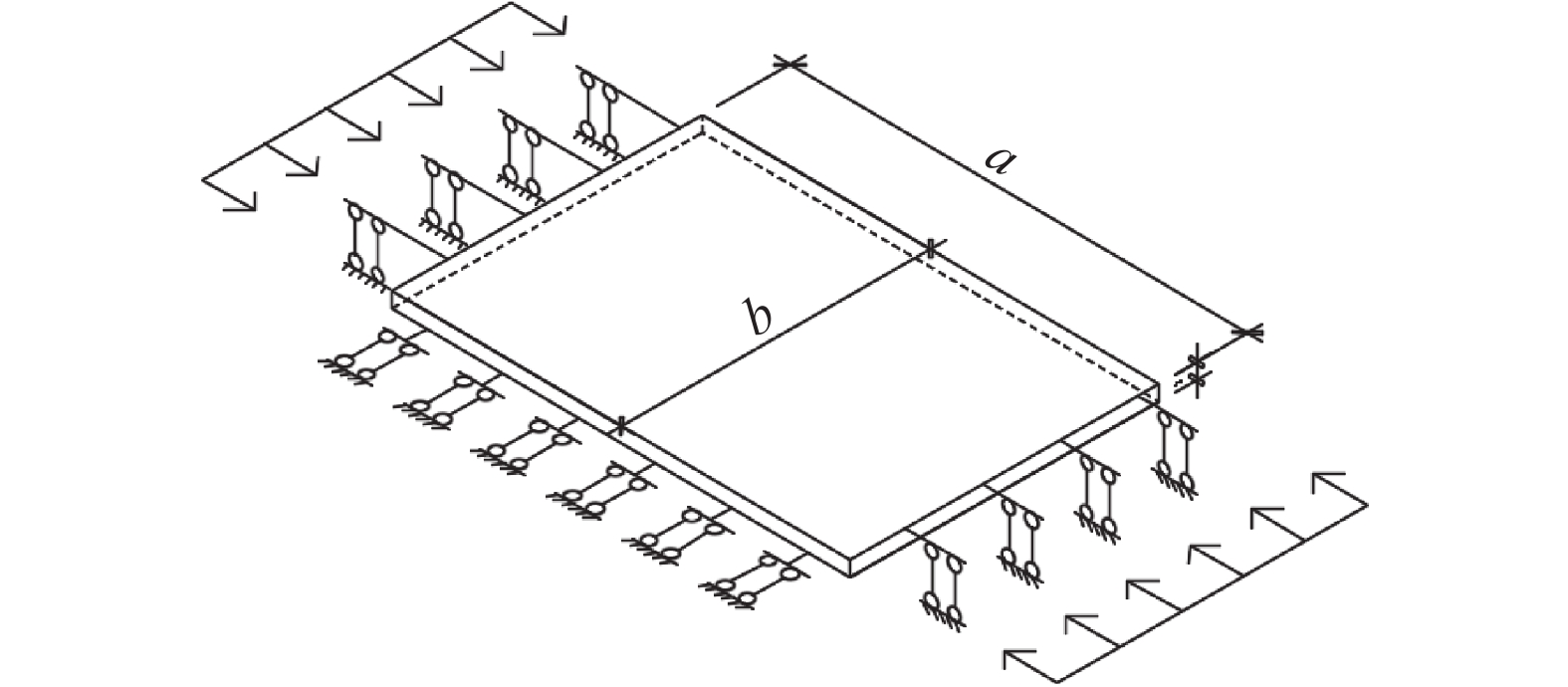
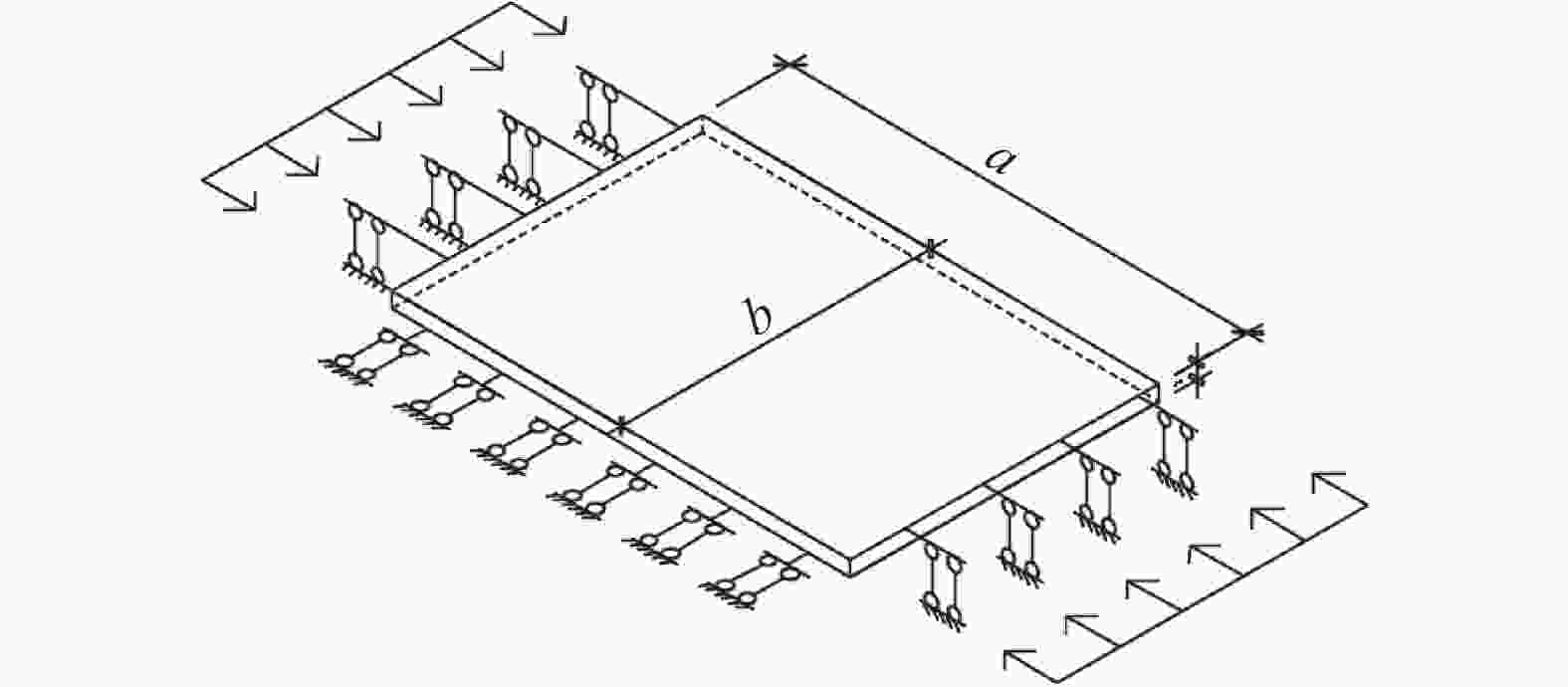
$\left( {\dfrac{1}{{80}}\sim \dfrac{1}{{100}}} \right) < \dfrac{t}{b} = \dfrac{1}{{14}} < \left( {\dfrac{1}{5}\sim \dfrac{1}{8}} \right)$ ,板的剪切变形与弯曲变形可忽略,可采用均匀受压板理论计算角钢肢翼缘的弹性屈曲承载力[19-21]。局部稳定计算简图如图12所示,所分析的轴压板边界条件为两加载边固定,非加载边一边自由一边固定。a和b分别为板受力方向边的长度和垂直受力方向边的长度,${P_x}$ 为轴向压力,计算局部屈曲临界应力取决于a、b和板的厚t以及加载边和非加载边的约束条件等。根据单向均匀受压矩形板建立平衡方程:
$$ D\left( {\dfrac{{{\partial ^4}w}}{{\partial {x^4}}} + 2\dfrac{{{\partial ^4}w}}{{\partial {x^2}\partial {y^2}}} + \dfrac{{{\partial ^4}w}}{{\partial {y^4}}}} \right) + {p_x}\dfrac{{{\partial ^2}w}}{{\partial {x^2}}} = 0 $$ (1) 式中:
x —受压方向的长度变量(mm);
y —沿垂直于受压方向的长度变量(mm);
D —单位宽度板的抗弯刚度(N·mm3),
$D = \dfrac{{E{t^3}}}{{12(1 - {\nu ^2})}}$ ;w —矩形板任意点的挠度(mm)。
根据四边简支矩形板边界条件:
当
$x = 0$ 和$x = b$ 时,$\omega = 0$ ,$\dfrac{{{\partial ^2}\omega }}{{{\partial ^2}x}} = 0$ ,$\dfrac{{{\partial ^2}\omega }}{{{\partial ^2}y}} = 0$ ;当
$y = 0$ 和$y = b$ 时,$\omega = 0$ ,$\dfrac{{{\partial ^2}\omega }}{{{\partial ^2}x}} = 0$ ,$\dfrac{{{\partial ^2}\omega }}{{{\partial ^2}y}} = 0$ 。可得四边简支板弹性屈曲条件:
$$ \dfrac{{{m^4}{{\text{π}} ^4}}}{{{a^4}}} + 2\dfrac{{{m^2}{n^2}{{\text{π}} ^2}}}{{{a^2}{b^2}}} + \dfrac{{{n^4}{{\text{π}} ^4}}}{{{b^4}}} - \dfrac{{{p_x}}}{D} \times \dfrac{{{m^2}{{\text{π}} ^2}}}{{{a^2}}} = 0 $$ (2) 式中:
px—屈曲荷载,
${p_x} = \dfrac{{{a^2}{{\text{π}} ^2}D}}{{{m^2}}}{\left( {\dfrac{{{m^2}}}{{{a^2}}} + \dfrac{{{n^2}}}{{{b^2}}}} \right)^2}$ 。板屈曲时垂直受力方向仅产生一个半波,而此时受力方向产生半波数m需使对应的屈曲荷载为最小值,将m视作弹性屈曲荷载的连续函数,求导得到其极值点
${P_{{\rm{crx}}}}$ 所对应$m = \dfrac{a}{b}$ ,因m的物理意义为受力方向对应的半波数,而$\dfrac{a}{b}$ 通常并不为整数,因此计算时m取值为与$\dfrac{a}{b}$ 接近且使${P_{{\rm{crx}}}}$ 最小的整数,因此弹性屈曲临界公式可表达为:$$ {p_x} = k \cdot \dfrac{{{{\text{π}} ^2}D}}{{{b^2}}} $$ (3) 式中:
k—屈曲系数,
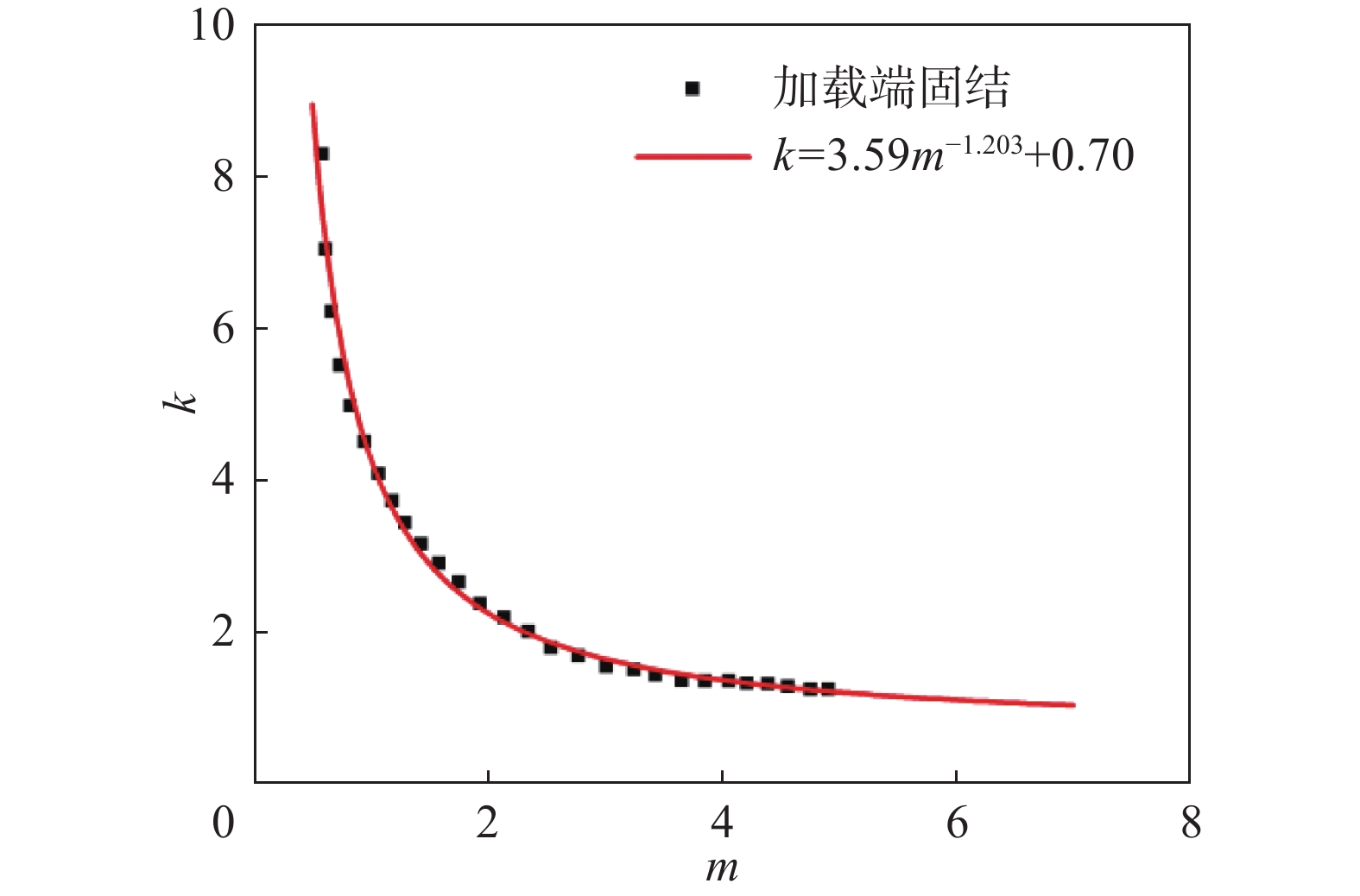
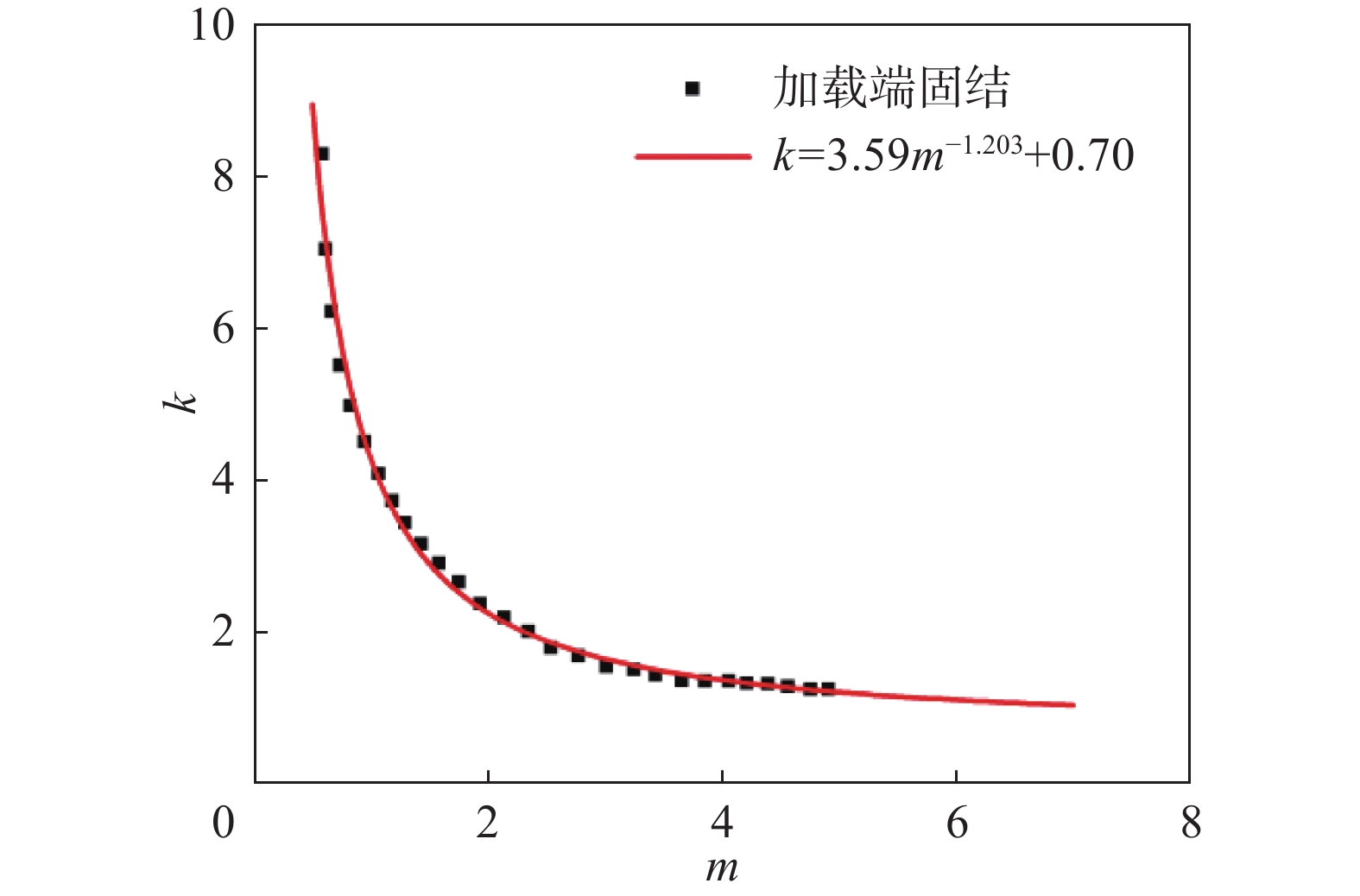
$k = {\left( {\dfrac{{mb}}{a} + \dfrac{a}{{mb}}} \right)^2}$ 。现有研究发现,当加载边为固定边界时,k值有所提高,因此将加载边固定,非加载边一边固定,一边自由所得k值曲线拟合,如图13所示。
-
由于主材角钢存在初始缺陷,理想薄板弹性屈曲理论计算得到的承载力偏大。基于验证的有限元分析结果与理想薄板弹性局部失稳承载力之比确定修正的局部稳定承载力计算方法,如表2所示,得到以构件长细比为自变量的修正局部稳定承载力
${P_{\max .{\rm{C}}}}$ 计算公式:试件编号 d×t/(mm×mm) 长度/mm 长细比 $ \mathrm{\xi } $ m k Pmax,C/kN Pmax,FEM/kN $\dfrac{ { {P_{\max .{\rm{C}}} } } }{ { {P_{\max .{\rm{FEM}}} } } }$ Rein4-1 L140×10 2500 45.05 0.42 2.64 1.81 1000.71 1000.80 1.00 Rein4-2 L140×10 3000 54.06 0.41 2.64 1.81 977.02 974.91 1.00 Rein4-3 L140×10 3500 63.07 0.40 2.64 1.81 953.24 950.79 1.00 Rein4-4 L140×10 4000 72.08 0.39 2.64 1.81 929.87 927.20 1.00 Rein4-5 L140×10 4500 81.10 0.38 2.64 1.81 907.11 905.34 1.00 Rein4-6 L140×10 5000 90.11 0.37 2.64 1.81 885.06 886.20 1.00 Rein4-7 L140×10 5500 99.12 0.36 2.64 1.81 863.73 863.38 1.00 Rein4-8 L140×10 6000 108.13 0.35 2.64 1.81 843.10 838.25 1.01 Test-Rein4-1 L140×10 2750 49.56 0.41 2.64 1.81 988.93 988.97 1.00 Test-Rein4-2 L140×10 3750 67.58 0.39 2.64 1.81 941.49 938.85 1.00 Test-Rein4-3 L140×10 4250 76.59 0.38 2.64 1.81 918.41 918.42 1.00 注:Rein4-1中,“Rein4”代表试件类型为角钢贴合槽钢(加固试件),“1、2……8”表示变长细比试件编号;Pmax, C表示公式计算承载力;Pmax, FEM表示有限元计算承载力;Test-Rein4-1中“Test-Rein4”代表验证试件,其类型为角钢贴合槽钢(加固试件),“1、2、3”表示验证试件编号。 Table 2. Calculation table of ideal elastic local stability bearing capacity
$$ \eta = \dfrac{{\ln \lambda }}{{10}} $$ (4) $$ \xi = - 3{\eta ^2} + 1.8\eta + 0.165 $$ (5) $$ {P_{\max ,{\rm{C}}}} = \xi \cdot k \cdot \dfrac{{{{\text{π}} ^2}D}}{{{b^2}}} $$ (6) 式中:
$\lambda $ —角钢长细比,$\lambda = \dfrac{l}{i}$ ;$i$ —角钢截面回转半径(mm),$i = \sqrt {\dfrac{I}{A}}$ ;k—屈曲系数,
$k = 3.59{m^{ - 1.203}} + 0.70$ ,$m = \dfrac{a}{b}$ ;a—受压方向加载端至屈曲位置最近螺栓的距离(mm),针对本文具体可取370 mm;
b—角钢肢宽(mm),针对本文具体可取140 mm。
-
根据上述得出的修正局部稳定承载力计算公式采用有限元计算承载力进行验证,验证模型构件分别为Test-Rein4-1、Test-Rein4-2和Test-Rein4-3,如表2所示。验证模型与计算公式所得承载力一致,证明修正局部稳定承载力计算公式可有效计算大长细比角钢贴合槽钢构件的极限承载力。
-
1)轴压荷载作用下,未加固角钢试件出现绕弱轴的整体弯曲并伴随截面扭转,呈现弯扭失稳破坏形式,荷载-位移曲线上升段未出现明显的非线性特征,达到失稳临界荷载后承载力迅速下降,构件发生弹性失稳。
2)轴压荷载作用下,角钢贴合槽钢试件主材角钢在端部加载区发生波浪形局部屈曲,荷载-位移曲线可划分为线性段与非线性段,临近失稳荷载时曲线具有明显的非线性,构件延性较好。
3)考虑构件侧向支撑结构建立有限元模型所反映构件的破坏形式与试验基本相同,所得荷载-位移曲线与试验符合良好,采用的模拟方法具有良好的准确性。
4)角钢贴合槽钢失稳模式随长细比变化不显著,均为加载端部区域主材角钢发生波浪状薄板局部失稳,试件承载力随长细比增大未出现大幅下降,该加固措施可有效提高大长细比构件的极限承载力。
5)基于理想薄板弹性失稳理论推导的、以构件长细比为自变量的修正局部失稳承载力计算公式具有良好的计算精度,可用于计算贴合槽钢加固措施下不同长细比角钢的极限承载力。
Research on Bearing Capacity of Angle Steel Transmission Tower Subject to Parallel Reinforcement by Fitting Channel Steel
doi: 10.16516/j.gedi.issn2095-8676.2023.02.016
- Received Date: 2022-05-08
- Rev Recd Date: 2022-08-30
- Available Online: 2023-03-13
- Publish Date: 2023-03-25
-
Key words:
- angle steel /
- transmission tower /
- parallel reinforcement /
- axial compression test /
- numerical simulation /
- calculation method of local buckling bearing capacity
Abstract:
| Citation: | LI Jinghui, LIU Xianghong, WANG Jiaqi, SUN Qing, ZHANG Donghong. Research on Bearing Capacity of Angle Steel Transmission Tower Subject to Parallel Reinforcement by Fitting Channel Steel[J]. SOUTHERN ENERGY CONSTRUCTION, 2023, 10(2): 119-128. doi: 10.16516/j.gedi.issn2095-8676.2023.02.016 |








































 DownLoad:
DownLoad: