-
当前,电力体制改革逐步深化,我国正加速构建以新能源为主体的新型电力系统[1]。从地理分布上看,我国新能源装机与负荷呈逆向分布,为满足新能源外送需求,我国电力系统实施“西电东送、南北互供、全国联网”的发展战略[2-3]。特高压直流输电技术凭借其输送容量大、输电距离远等独特优势成为电力输送的重要方式,电网呈现出“强直弱交”新特性[4]。LCC-HVDC(Line-Commutated Converter High Voltage Direct Current,LCC高压直流输电)输电系统作为目前广泛使用的直流输电形式,其输送容量正不断增加[5-6]。为保障交直流系统的安全性和供电可靠性,需要为直流换流站提供足够的无功功率,正常运行下,整流器需要的无功功率约为直流传输有功功率的30%~50%,逆变器需要的无功功率约为直流传输有功功率的40%~60%[7]。无功不足可导致换相失败、暂态过电压等问题,威胁电网安全稳定[8-10]。
现有换流站无功优化研究主要围绕交流滤波器配置方案和通过直流控制优化投切方案展开。文献[11]基于离散调压设备动作的影响因素,提出一种考虑离散调压设备动作频次的高压直流输电系统改进控制策略。文献[12]基于交直流混联系统解耦求解思想,提出一种换流站最优交流滤波器投入组数及交直流系统最优无功功率交换量的确定方法。文献[13]就减小交直流电网无功交换方法开展研究,分析了换流站无功消耗与直流功率、直流电压、触发角、熄弧角的关系。文献[14]研究了交流滤波器配置的合理性和投切控制的优先级别,实现投切控制功能的优化。文献[15]分析了无功补偿设备的动作特性,提出以减小事故后稳态电压越限水平和分接开关动作次数为目标的无功协调控制策略。上述研究仍局限于交流滤波器独立承担换流站无功补偿和无功调整,调相机仍然定位为系统故障期间的动态无功支撑设备,未能明确两者在稳态过程的协调配合问题。
基于上述LCC-HVDC换流站内调相机和交流滤波器的应用场景各自独立的情况,文章提出在不影响调相机动态特性的前提下,由调相机置换部分交流滤波器容量,参与稳态无功补偿,优化换流站交流滤波器的投入组数。在交直流系统间无功交换量越限,需要进行无功调整时,提出由调相机与换流站交流滤波器根据动作先后建立的双层无功调整策略替代目前交流滤波器单独投切进行无功调整的策略。双层无功调整策略下,根据调相机预设稳态出力范围和实际运行情况计算其可调出力量,据此将无功调整总量分配为第一层和第二层无功调整量。第一层无功由调相机承担,在预设的稳态运行范围内调整出力,减少交直流系统间无功交换量,随后进行判定修正,若交直流系统间无功交换量仍然越限,则第二层无功调整启动,逐组投切交流滤波器直至交直流系统间无功交换量符合要求。最后,通过仿真验证所提策略的有效性和优势。
-
与同容量的发电机组相比,特高压直流大规模馈入受端系统的动态无功储备显著下降,电压稳定问题愈显突出[16]。为提高弱送端高压直流运行的稳定性和直流输送能力,需要加装额外的无功补偿装置。调相机作为直流输送中理想的无功补偿设备,具有良好的无功输出特性,在降低直流送端暂态过电压,抑制直流受端暂态低电压和直流受端换相失败,利用强励提高系统稳定性等方面具有独特的优势[17-19]。此外,作为空载运行的大型同步电动机,大容量调相机还可为薄弱的特高压直流送端系统提供一定的短路容量和转动惯量支撑[20]。下面就调相机稳态与故障下的出力进行分析。
-
调相机本质是一台同步发电机,根据发电机惯例,计及升压变电抗,其电压方程为:
$$ {\boldsymbol{E}}_{0}^{} = {\boldsymbol{U}} + {{j}}{\boldsymbol{I}}({X_{\rm{S}}} + {X_{\rm{T}}}) $$ (1) 式中:
E0 ——调相机励磁电动势(kV);
U ——经升压变并网电电压(kV);
I ——为调相机定子电流(kA);
XS ——调相机同步电抗(Ω);
XT ——升压变电抗(Ω)。
在dq0坐标系下,由同步电机电压基本方程,调相机无功功率表达式为:
$$ {{Q}_{{\text{SC}}}}{\text{ = }}UI $$ (2) 图1为稳态下调相机并网等值电路。
由等值电路可得定子电流I:
$$ I = \frac{{{E_0} - U}}{{{{X}_{d}}{ + }{{X}_{\text{T}}}}} $$ (3) 实际中调相机定子电阻很小,可以忽略,由同步电压基本方程可知定子电流q轴分量近似于0,则:
$$ {I_{d}}{ = }I = \frac{{{E_0} - U}}{{{{X}_{d}}{ + }{{X}_{\text{T}}}}} $$ (4) 将公式(4)代入式(2),得稳态下调相机出力QSC为:
$$ {Q_{{\text{SC}}}} = \frac{{U({E_0} - U)}}{{{{X}_{d}}{ + }{{X}_{\text{T}}}}} $$ (5) 当稳态下进行调整时,设并网电电压保持恒定,调节调相机励磁系统,其出力变为
${Q_{\rm{SC}}^{''}}$ :$$ Q_{{\text{SC}}}^{''} = \frac{{U(E_0^{''} - U)}}{{{{X}_{d}}{+ }{{X}_{\text{T}}}}} $$ (6) 式中:
$E_0^{''}$ ——调节后调相机励磁电动势(kV)。由式(5)、式(6)可得稳态下调相机出力变化量为:
$$ \Delta Q_{{\text{SC}}}^{} = Q_{{\text{SC}}}^{''} - Q_{{\text{SC}}}^{} = \frac{{U(E_0^{''} - {E_0})}}{{{{X}_{d}}{ + }{{X}_{\text{T}}}}} $$ (7) -
图2为系统扰动下调相机并网等值电路,
$E_q^{''} $ 为调相机q轴次暂态电动势,${X}_{d}^{''} $ 为d轴次暂态电抗,${X}_{\text{T}} $ 为调相机升压变电抗。系统发生故障时,并网电电压发生突变,调相机等效为内电阻恒定的电压源,$E_0 = E_q^{''}$ 。根据等值电路,可得Id为:
$$ {I_{d}} = \frac{{E_{q}^{''} - U}}{{{X}_{d}^{''}{ + }{{X}_{\text{T}}}}} $$ (8) 将式(8)代入式(2),则故障前调相机出力计算公式:
$$ {Q_{{\text{SC}}2}} = \frac{{U(E_{q}^{''} - U)}}{{{X}_{d}^{''}{ + }{{X}_{\text{T}}}}} $$ (9) 当交流系统发生故障,并网电电压越限时,图2中并网点电压由U变为Um,此时调相机出力为:
$$ Q_{{\text{SC2}}}^{''} = \frac{{{U_{\text{m}}}(E_{q}^{''} - {U_{\text{m}}})}}{{{X}_{d}^{''}{ + }{{X}_{\text{T}}}}} $$ (10) 由式(3)、式(4)可得,故障下调相机无功功率变化量:
$$ \Delta {Q}_{\text{SC2}}^{}={Q}_{\text{SC2}}^{''}-{Q}_{\text{SC2}}^{}=\frac{{U}_{\text{m}}^{\text{2}}-{U}_{\text{m}}+{E}_{q}^{''}({U}_{\text{m}}-U)}{{X}_{d}^{''}{+ X}_{\text{T}}} $$ (11) -
交流滤波器是换流站内提供无功补偿的主要设备,同时能滤除换流站产生的谐波。换流站内交流滤波器配置方案要基于占地、投资和投切后电压平衡综合考虑,根据总容量和单组容量,组数通常设置在8~15组[21]。交流滤波器的投切通过直流输电控制系统中配置的无功控制实现投切,保持交直流系统间无功交换量Qexc处于允许范围内。此外,为限制交流滤波器出现频繁投切的情况,交流滤波器设置有投切死区值Qdz,可根据实际工况修改,Qdz通常为单组滤波器容量的65%~80%[22]。
工况下,单组交流滤波器的无功出力Qfilt的计算公式为:
$$ Q_{{\rm{filt}}} = {\left( {\frac{{U_{\rm{p}}^{}}}{{{U_{\rm{N}}}}}} \right)^2}{Q_{{\rm{filtN}}}} $$ (12) 式中:
Up ——交流母线实际电压(kV);
UN ——交流母线额定电压(kV);
QfiltN——单组交流滤波器额定容量(Mvar)。
在n组交流滤波器投入运行的情况下,交直流系统间无功交换量Qexc:
$$ Q_{{\text{exc}}}^{} = {Q_{{\text{ac}}}} + {n}{Q_{{\text{filt}}}}{ - }{Q_{{\text{conv}}}} $$ (13) 式中:
Qac ——交流系统注入无功(Mvar);
Qconv——换流站无功消耗量(Mvar)。
当Qexc>Qdz时,控制系统动作切除一组交流滤波器,当Qexc<−Qdz时,控制系统动作投入一组交流滤波器,直至满足−Qdz<Qexc<Qdz,交流滤波器不再动作。
当系统发生故障,换流站母线电压发生波动时,单组交流滤波器无功出力变为:
$$ Q_{{\rm{filt}}}^{'} = {\left(\dfrac{{U_{\rm{p}}^{'}}}{{{U_{\rm{N}}}}}\right)^2}{Q_{{\rm{filtN}}}} $$ (14) 在滤波器投入组数为n组的情况下,故障后由交流滤波器引发的换流站无功缺额或盈余为:
$$ \Delta Q = {n(}Q_{{\rm{filt}}}^{'} - Q_{{\rm{filt}}}^{}) = {n}\frac{{U_{\rm{p}}^{'2} - U_{\rm{p}}^{2}}}{{U_{\rm{N}}^{2}}}{Q_{{\rm{filtN}}}} $$ (15) -
为提高调相机的利用率,文章提出将调相机作为换流站稳态无功补偿设备之一。由于LCC-HVDC系统受端与送端在故障时面临的问题存在差异,送、受端换流站动态过程中对调相机的需求不同,因此基于调相机的受端与送端换流站无功补偿优化方案需要分别讨论。
-
高压直流送端大多建在新能源集中地区,系统较弱,暂态下主要面临过电压问题。系统故障引起换相失败甚至直流闭锁,引发送端过电压。由式(12)可知,交流滤波器无功输出能力与交流母线电压的平方成正比,母线电压升高,交流滤波器无功出力增加,暂态下无功盈余进一步增加,暂态过电压峰值随之上升。因此,减少滤波器投入组数有利于减小暂态过电压。送端换流站要求调相机拥有足够的进相运行能力,以应对故障下送端系统过电压问题。调相机置换部分交流滤波器容量后处于滞相运行状态,故障下调相机能够发出更多的容性无功,这与动态过程下对调相机的要求相适应。
上述分析论述了调相机参与送端换流站无功补偿方案的可行性与优势,下面介绍送端换流站具体无功补偿方案。调相机参与换流站无功补偿前,换流站内无功补偿总量为QR:
$$ {Q_{\rm{R}}} = n{\left(\dfrac{{{U_{\rm{p}}}}}{{{U_{\rm{N}}}}}\right)^2}{Q_{{\rm{filtN}}}} + {Q_{\rm{C}}} $$ (16) 其中:QC为换流站除交流滤波器和调相机外其余无功补偿装置提供的补偿总量。引入调相机参与送端换流站稳态无功补偿后,单台调相机稳态出力QSC与交流滤波器间的协调约束如下:
$$ \left\{ {\begin{array}{*{20}{l}} {0 \leqslant {Q_{{\rm{SC}}}} \leqslant m{Q_{{\rm{filtN}}}} + {Q_{{\rm{dz}}}} \leqslant {Q_{{\rm{SCN}}}}} \\ {0 \leqslant m \leqslant \dfrac{{{Q_{{\rm{SCN}}}} - {Q_{{\rm{dz}}}}}}{{{Q_{\rm{filtN}}}}}} \\ {m \in {\boldsymbol{Z}}} \end{array}} \right. $$ (17) 式中:
m ——调相机与交流滤波器间的协调系数;
QSCN——调相机额定容量(Mvar)。
m的物理意义为调相机置换的交流滤波器组数,针对新一代大容量调相机QSCN通常取300 Mvar。在配置调相机台数为q的换流站中,调相机参与无功补偿后有:
$$ {Q_{\rm{R}}} = \left(n - \sum\limits_{i = 1}^{i = q} {{m_i}} \right){\left(\dfrac{{{U_{\rm{p}}}}}{{{U_{\rm{N}}}}}\right)^2}{Q_{{\rm{filtN}}}} + \sum\limits_{i = 1}^{i = q} {{Q_{{\rm{SC}}{{i}}}} + } {Q_{\rm{C}}} $$ (18) 由式(16)和式(18)可知,调相机参与送端换流站无功补偿可以减少交流滤波器投入组数,进一步由式(15)可知,上述方案可以减小暂态过电压下交流滤波器产生的无功盈余量,进而降低送端系统暂态过电压峰值。
-
高压直流受端多建在负荷中心,通常存在多馈入现象,直流受端在故障时主要问题为无功支撑不足,面临低电压问题,为保证系统稳定,减小故障下的电压跌落,应尽量减少交流滤波器的切除,适当增加交流滤波器的投入组数。受端系统的调相机需要有足够的动态无功储备以抑制故障下受端系统低电压问题,调相机在进相运行下可提高动态无功储备,更好抑制暂态低电压。
据此分析受端换流站内调相机与交流滤波器的协调无功补偿方案:为实现较多交流滤波器组的投入,直流受端换流站无功补偿方案应以交流滤波器组为主补偿,调相机进相运行,增加交流滤波器投入组数,并提高调相机在低电压下的电压支撑能力。调相机进相运行下,受端换流站内无功补偿总量QI:
$$ Q_{\rm{I}} = {n^{'}}{\left(\dfrac{{U_{\rm{p}}}}{{{U_{\rm{N}}}}}\right)^2}{Q_{{\rm{filtN}}}} + Q_{\rm{C}}^{'} $$ (19) 式中各量物理意义可参考式(16),引入调相机参与受端换流站稳态无功补偿后,单台调相机稳态出力QSC与交流滤波器间的协调约束如下:
$$ \left\{ {\begin{array}{*{20}{l}} { - \alpha {Q_{{\rm{SCN}}}} \leqslant - ({m^{'}}{Q_{{\rm{filtN}}}} + {Q_{{\rm{dz}}}}) \leqslant {Q_{{\rm{SC}}}} \leqslant 0} \\ {0 \leqslant {m^{'}} \leqslant \dfrac{{\alpha {Q_{{\rm{SCN}}}} - {Q_{{\rm{dz}}}}}}{{{Q_{{\rm{filtN}}}}}}} \\ {{m^{'}} \in {Z{\boldsymbol{}}}} \end{array}} \right. $$ (20) α为调相机进行运行与滞相运行能力之比,新一代大容量调相机进相能力可达200 Mvar。受端换流站配置调相机台数为p时,调相机参与无功补偿后有:
$$ Q_I^{} = \left(n - \sum\limits_{i = 1}^{i = p} {m_i^{'}} \right){\left(\dfrac{{U_{\rm{p}}}}{{U_{\rm{N}}}}\right)^2}{Q_{{\rm{filtN}}}} + \sum\limits_{i = 1}^{i = p} {{Q_{{{\rm{SC}}{i}}}} + } {Q_{\rm{C}}} $$ (21) 由式(19)和式(21)可知,调相机参与受端换流站无功补偿可以增加交流滤波器投入组数,提高低电压下的电压支撑能力,进一步由式(15)可知,上述方案可以减小受端系统暂态低电压下交流滤波器的无功缺额量,进而抑制受端系统暂态低电压。
-
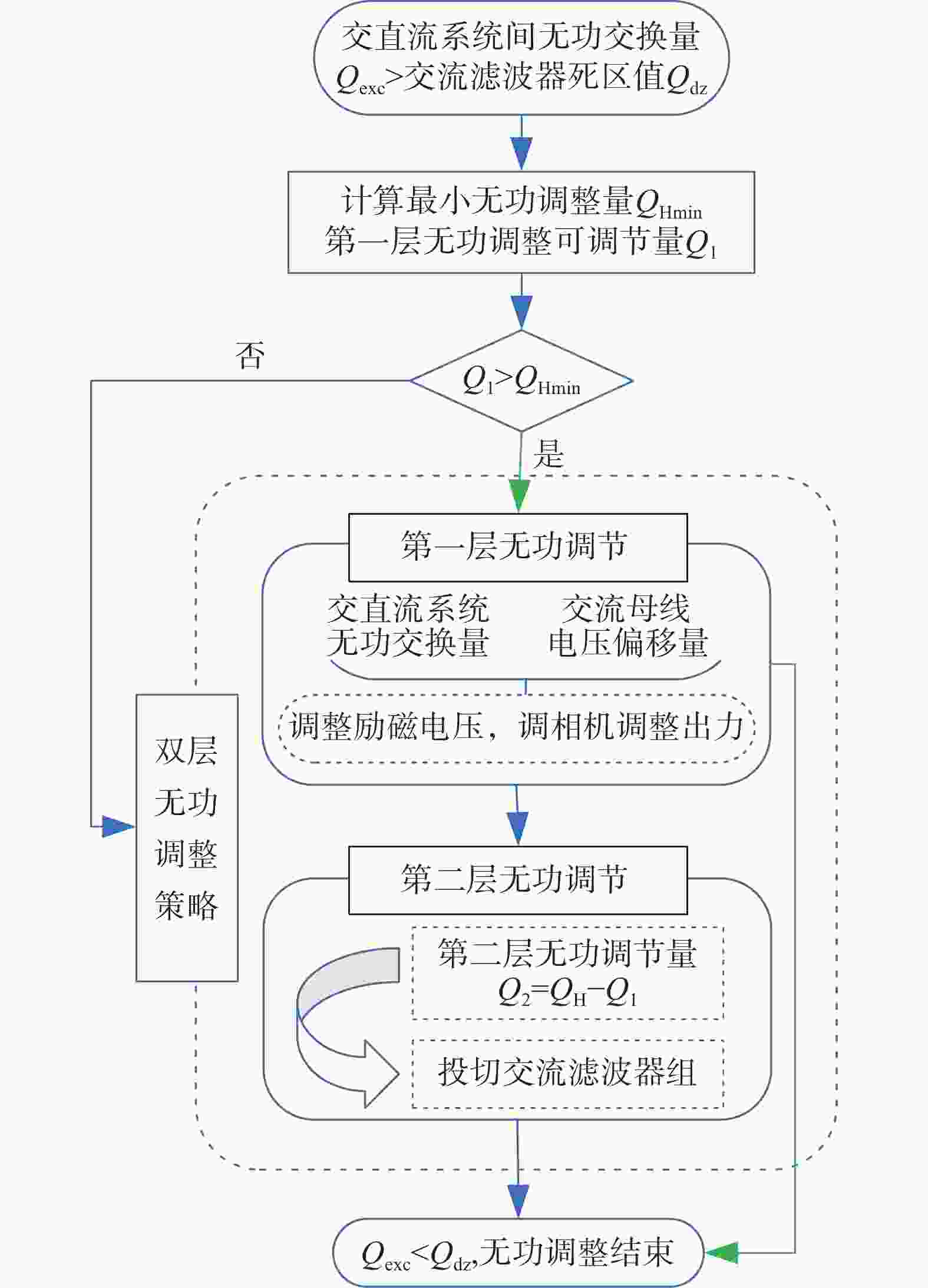
当系统发生负荷变化、线路投切等情况时,交流母线电压和交直流系统间无功交换量也随之发生变化,为保证系统安全稳定运行,需要进行无功调整。基于动作顺序,本节提出了一种换流站双层无功调节策略,在保障调相机动态支撑能力的前提下,引入调相机参与稳态无功补偿和调整。
引入调相机参与稳态无功补偿后,设调相机稳态出力为QSC,由式(13)可得该方案下交直流系统间无功交换量:
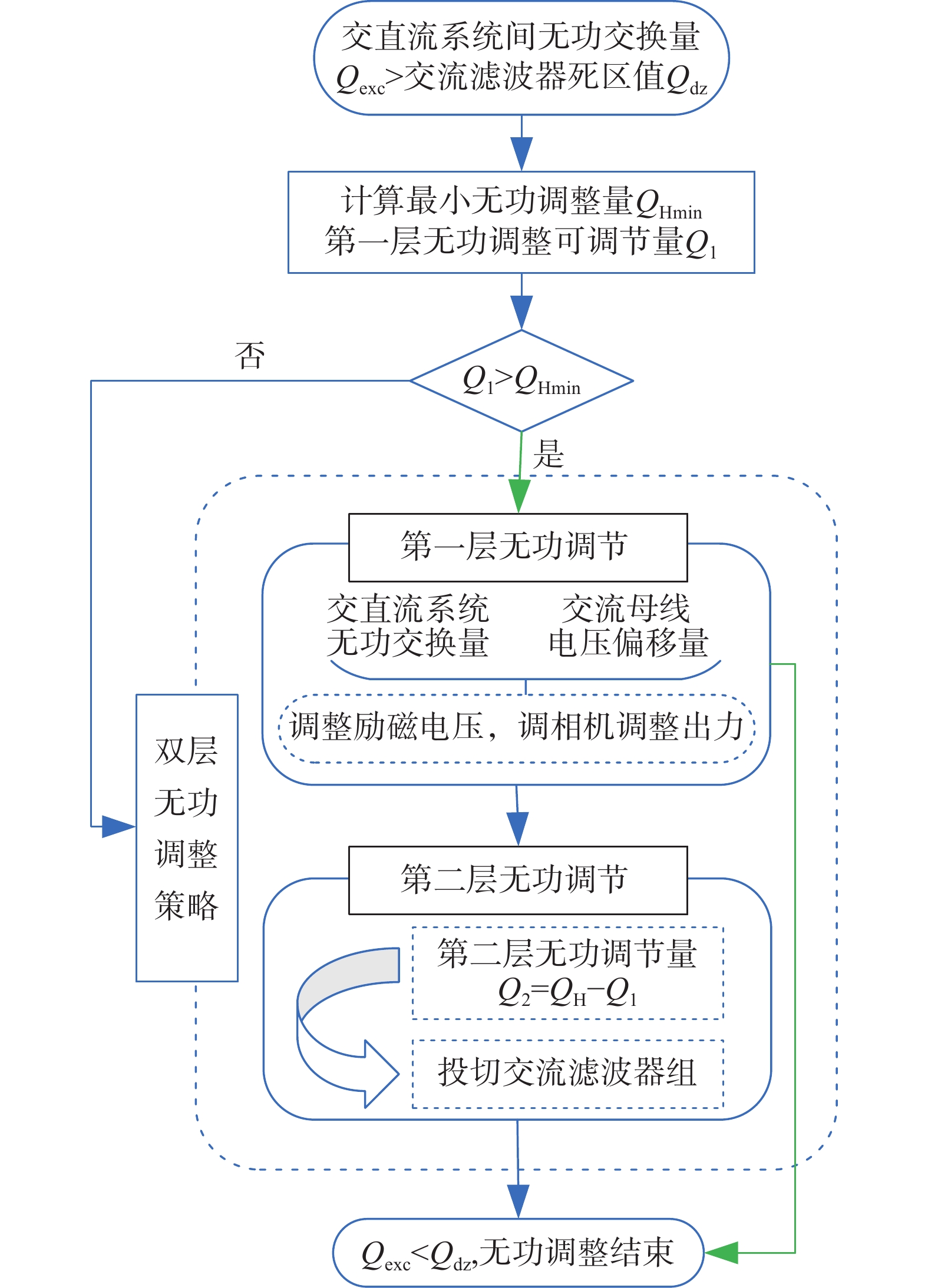
$$ Q_{{\text{exc}}}^{} = {Q_{{\text{SC}}}}{\text{ + }}{Q_{{\text{ac}}}} + {n}{Q_{{\text{filt}}}}{ - }{Q_{{\text{conv}}}} $$ (22) 当交直流系统间无功交换量Qexc大于换流站交流滤波器死区值Qdz时,交流滤波器将动作以进行无功调整,交流滤波器频繁投切会减少其使用寿命,提升换流站运行成本。基于上述调相机参与换流站无功补偿方案,为充分发挥调相机的稳态无功调整能力,减少交流滤波器投切频次,本节对调相机与交流滤波器协调开展稳态无功调整策略展开研究,提出两者协调下的双层无功调整策略。该方案下调相机稳态出力应根据换流站单组交流滤波器容量,保持在交流滤波器1~2组死区值附近或进相运行和滞相运行能力的50%以内,以保证调相机有足够无功裕度参与后续无功调整以及暂态下的动态支撑能力。图3为双层无功调整策略图示。
图中QHmin为最小无功调整量,无功调整范围可由下式计算:
$$ \left\{ {\begin{array}{*{20}{c}} {{{Q}_{{\text{Hmin}}}}{\text{ = |}}{{Q}_{{\text{exc}}}}\text{|}-{{Q}_{{\text{dz}}}}} \\ {{{Q}_{{\text{Hmax}}}}{\text{ = |}}{{Q}_{{\text{exc}}}}{\text{|} + }{{Q}_{{\text{dz}}}}} \\ {{{Q}_{{\text{Hmin}}}}{\text{ < }}{{Q}_{\text{H}}}{\text{ < }}{{Q}_{{\text{H}}\max }}} \end{array}} \right. $$ (23) 双层无功调节策略下调相机与交流滤波器协调进行无功调整。当Qexc>Qdz时,无功调整流程启动,根据调相机出力情况计算出第一层无功可调整量Q1,并与QHmin进行比较判定。
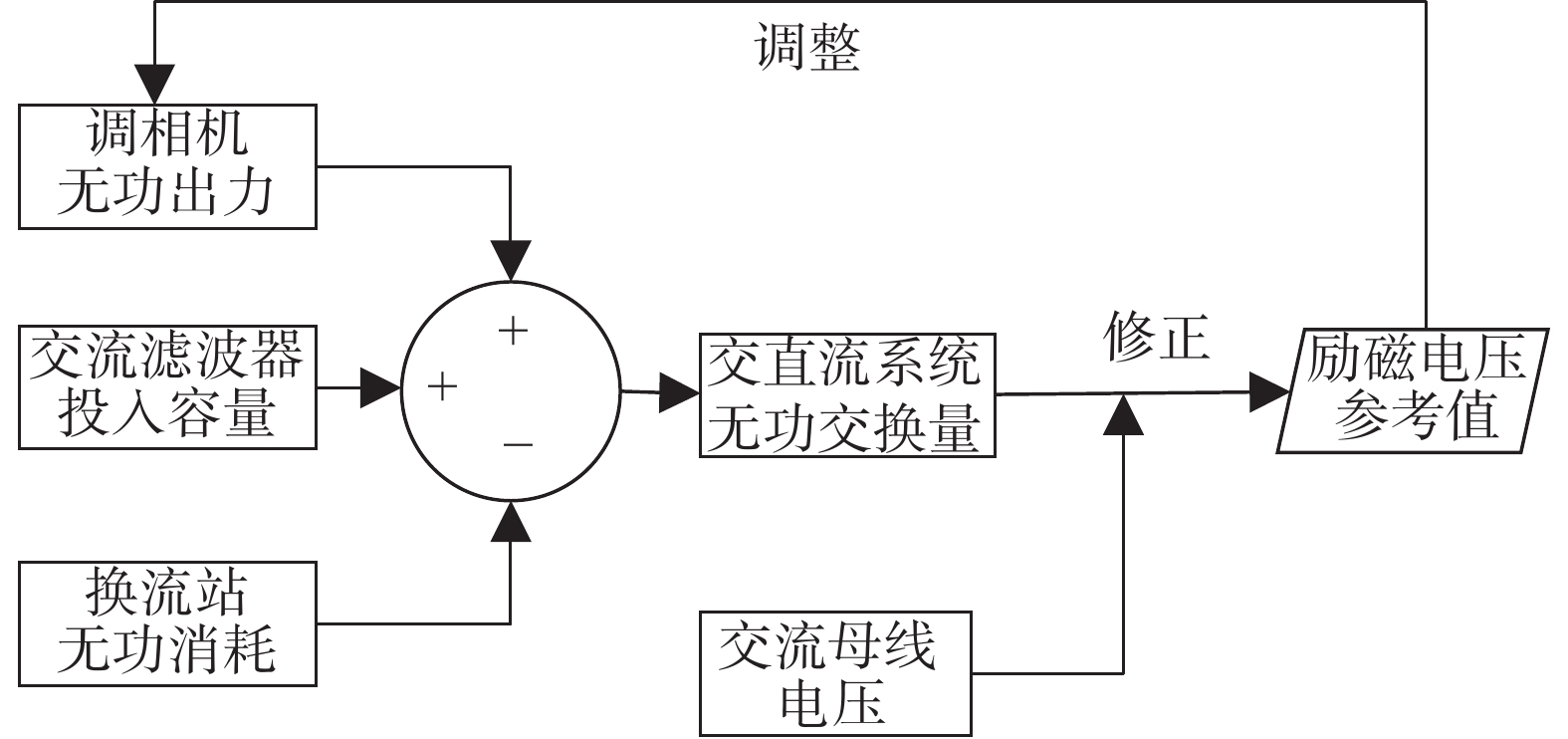
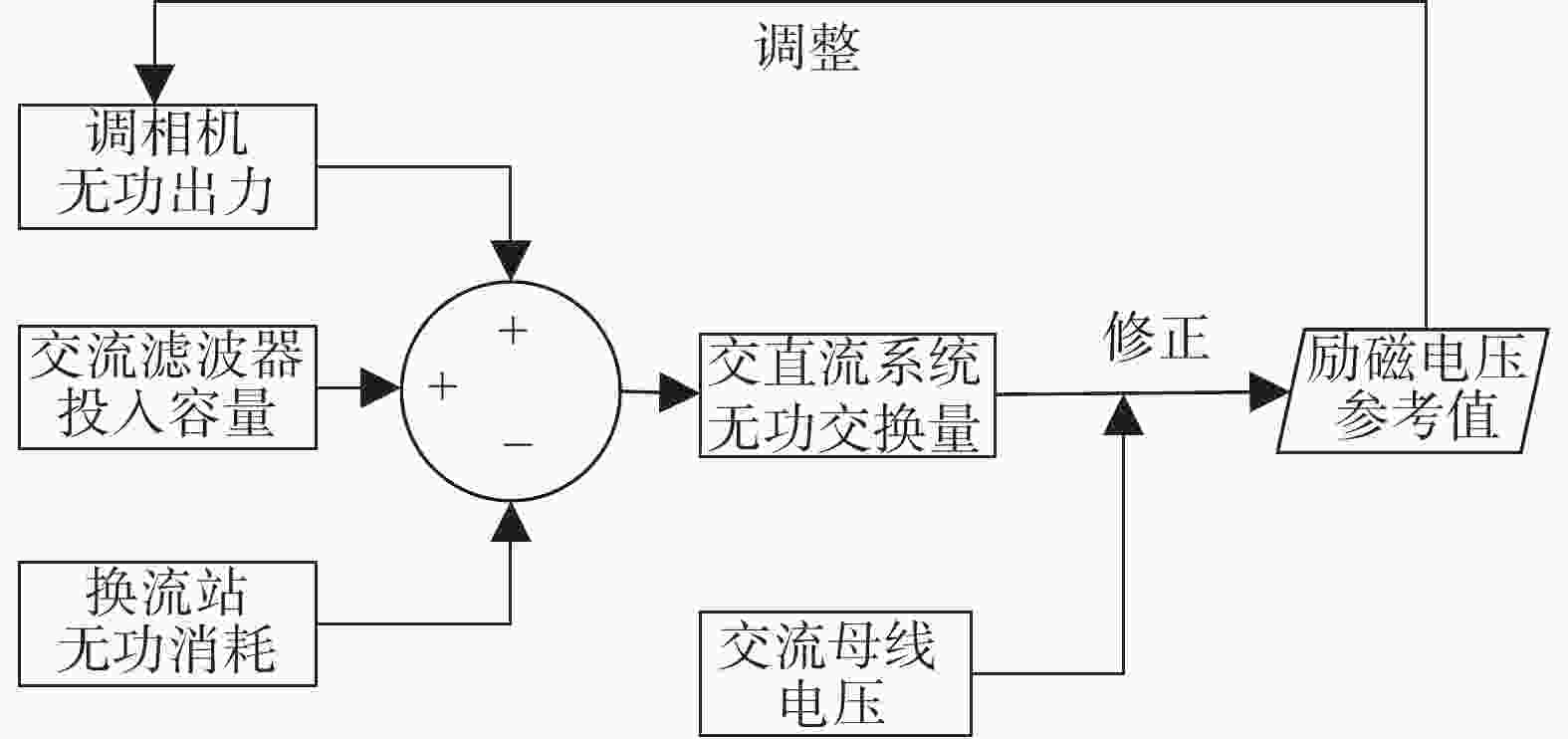
当Q1>QHmin,则双层无功调整策略下仅需第一层无功调节启动,即可满足无功调整需求:由调相机在预先设置的稳态出力范围内进行调整,根据电压偏移量和交直流系统间的无功交换量,对调相机励磁系统进行调整,从而调整调相机无功出力,使电压保持在稳定范围内,同时使Qexc<Qdz。第一层无功调节过程如图4所示。
当Q1<QHmin时,表明调相机稳态无功调整能力不足以使交直流系统间无功交换量达到稳定要求,需采用双层无功调整策略,为实现更好的协调配合,首先计算第二层无功调整需投切的交流滤波器组数a:
$$ a=\min \left\{a \mid a \geqslant \frac{Q_{{\rm{H}} \min }-Q_1}{Q_{\rm {filt }}}, a \in {\boldsymbol{Z}}\right\} $$ (24) 随后进行校验,若
${a}{{Q}_{{\text{filt}}}}{\text{ > }}{{Q}_{{\text{Hmax}}}}-{{Q}_{1}}$ ,则无功调整后Qexc仍无法达到要求,应适当减小调相机在第一层无功调整时的调整量。第一层无功调节结束后,交流滤波器承担第二层无功调节任务,为减小滤波器投切对系统带来的扰动,需将a组滤波器逐组投切,完成第二层无功调整。此外,根据新一代大容量调相机设计要求,采用双层无功调整策略时,若分接开关不动作,调相机在进行第一层无功调节时可以小幅度短时运行在稳态出力范围外,在第二层调节结束后交流母线电压将自动对调相机励磁电压进行修正,使其进入稳态运行范围。
-
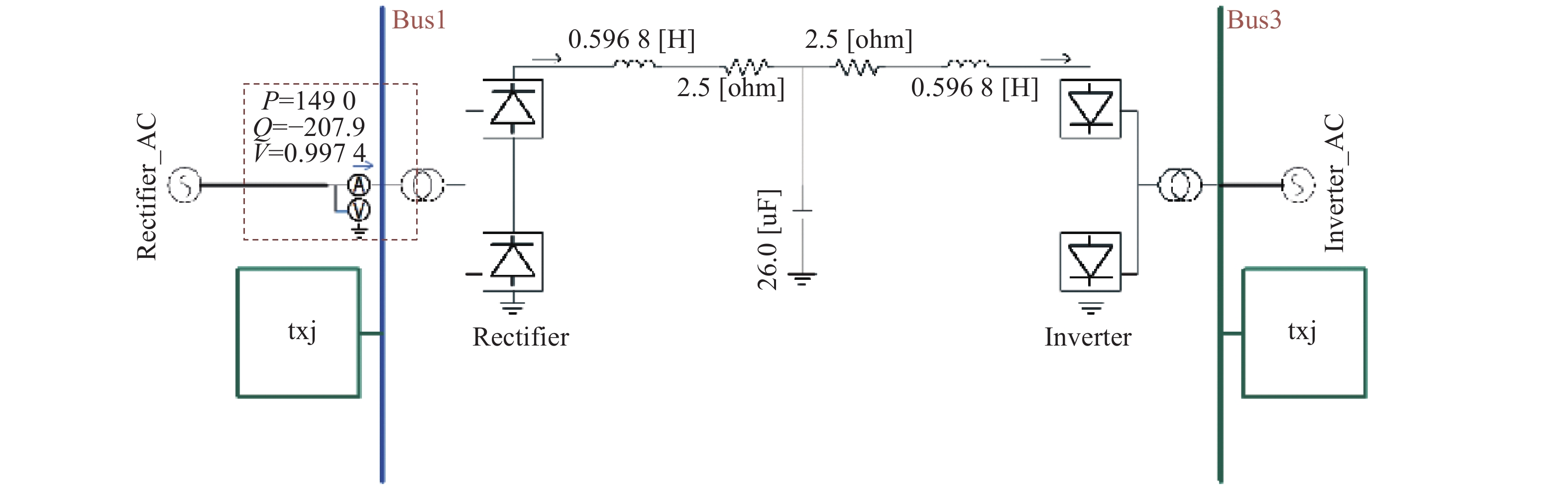
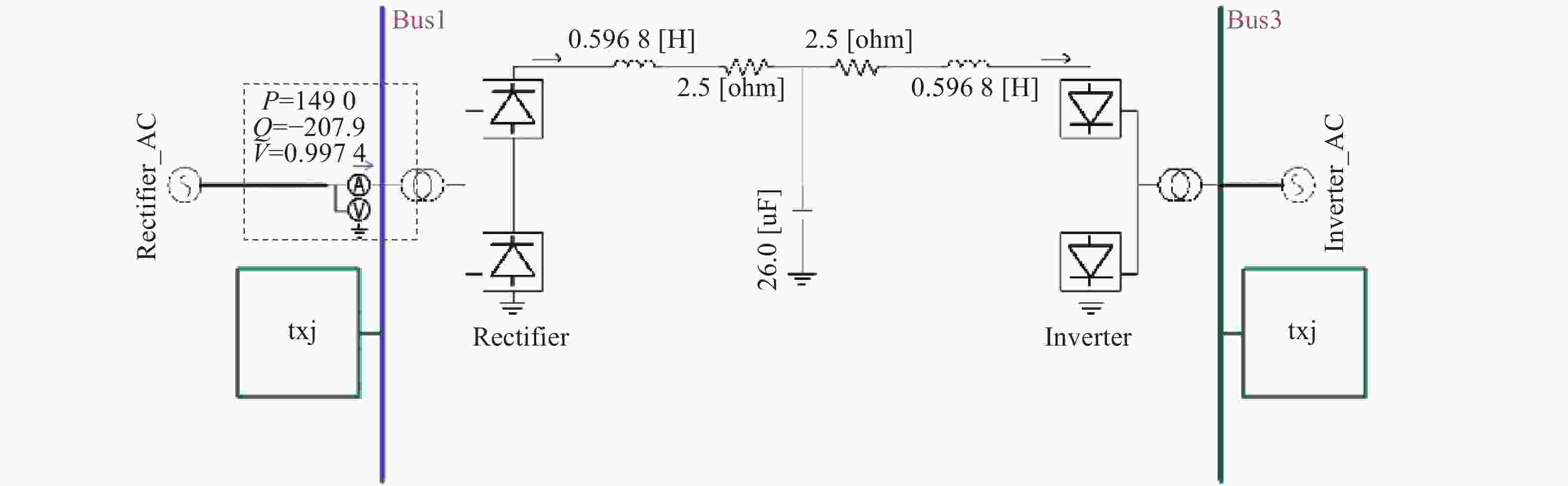
在PSCAD中搭建单极LCC-HVDC直流系统仿真模型如图5所示。直流容量为1500 MW,额定电压为500 kV,送、受端均包括同步机和调相机,送端交流系统额定电压为330 kV,受端交流系统额定电压为220 kV,本节就上述提出的换流站无功补偿优化方案和双层无功调整策略的有效性开展仿真验证。
-
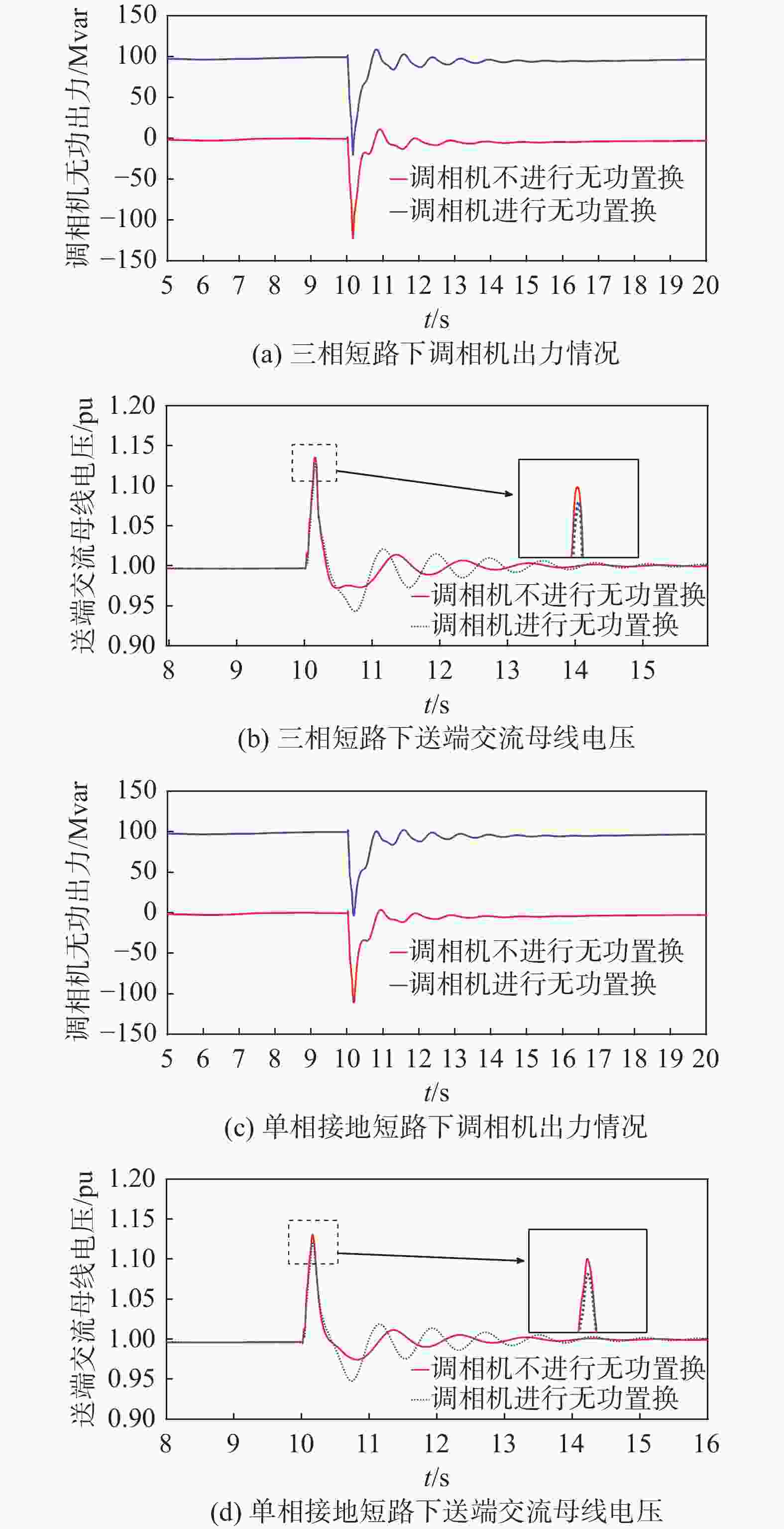
首先验证送端无功补偿方案下换流站调相机的动态特性,直流送端在暂态下面临过电压问题,由文献[23]和文献[24]可知,送端暂态过电压主要与交流滤波器容量、短路类型有关。为验证不同故障类型下方案的有效性,在受端母线处分别设置单相接地短路、三相短路故障,短路时间均为0.1 s,对比调相机在稳态出力为0和稳态下滞相运行,出力为100 Mvar下的动态支撑能力和两种情况下系统的电压稳定性。图6为两种运行方式下调相机的出力情况和送端交流母线电压。
由上述实验和图形可知,调相机稳态下滞相运行不影响调相机暂态下的快速响应能力和交流系统电压稳定性,且可以增加进相运行深度,文章所提送端换流站无功补偿方案下暂态过电压峰值降低。
随后在PSCAD模型中对比送端换流站在不同直流送出容量下,不同无功配置方案所需滤波器情况,方案一为仅由交流滤波器提供无功补偿,单组交流滤波器额定容量140 Mvar,方案二为调相机与交流滤波器共同参与换流站无功补偿任务,单组交流滤波器额定容量同方案一一致。两种配置方案下交流滤波器配置情况如表1。
直流容量/GW 调相机台数 方案一 方案二 2 1 6组 5组 3 1 11组 10组 4 2 12组 9组 6 3 21组 17组 8 4 25组 19组 Table 1. Input of AC filter at the sending converter station under different configuration schemes
由表1可知,在送端换流站,由调相机与交流滤波器在送端共同进行无功补偿,可以对交流滤波器进行部分无功置换,减少交流滤波器的投入组数。上述仿真表明调相机参与送端换流站稳态无功补偿的方案能够对换流站无功补偿方案实现优化。
-
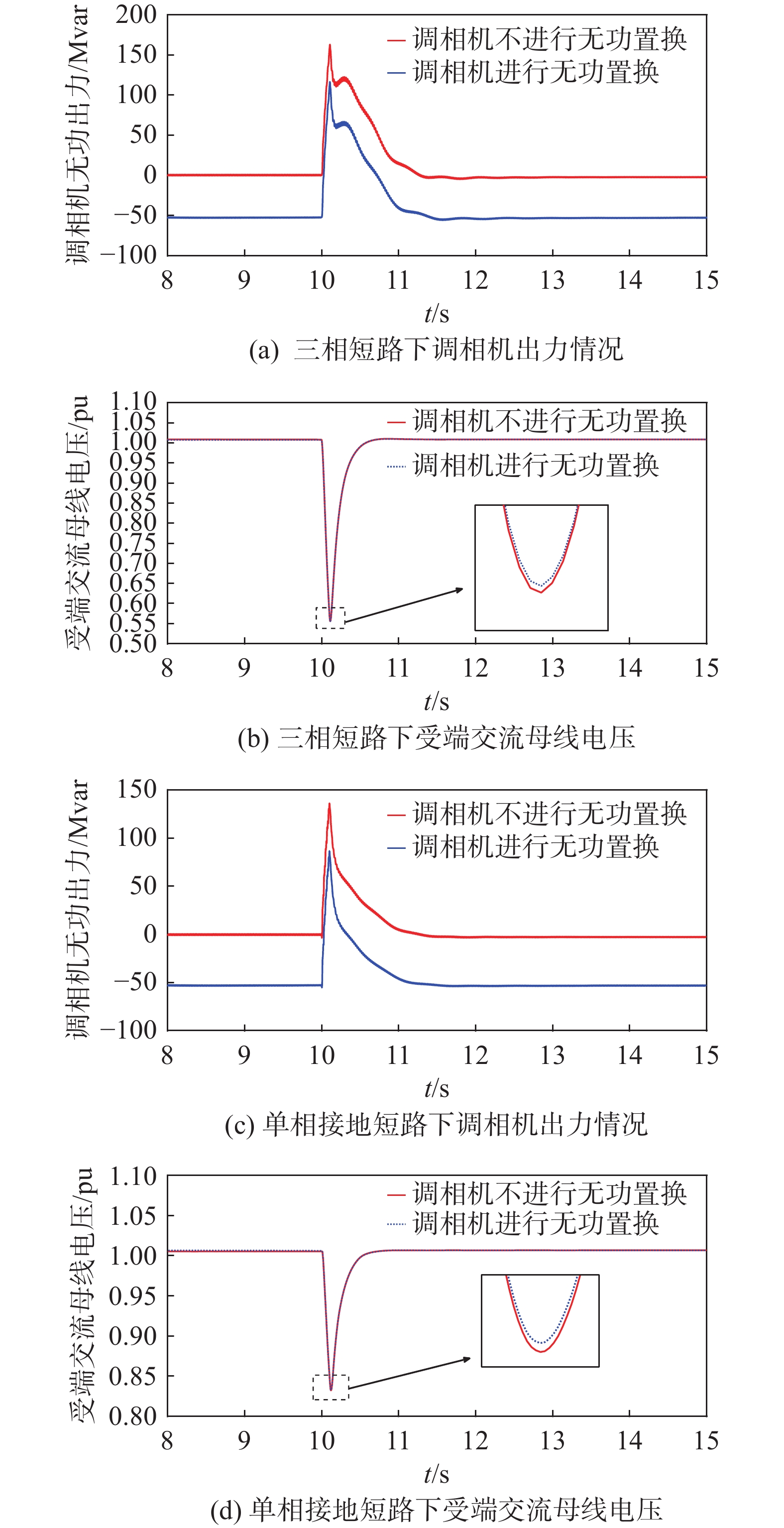
验证受端无功补偿方案中调相机的暂态无功支撑能力。在仿真模型中,10 s时在受端母线上发生三相短路故障,短路时间为0.1 s,对比调相机在稳态出力为0和稳态下进相运行−50 Mvar下的动态支撑能力及两种情况下系统的电压稳定性。图7为两种运行方式下调相机的出力情况和受端交流母线电压。
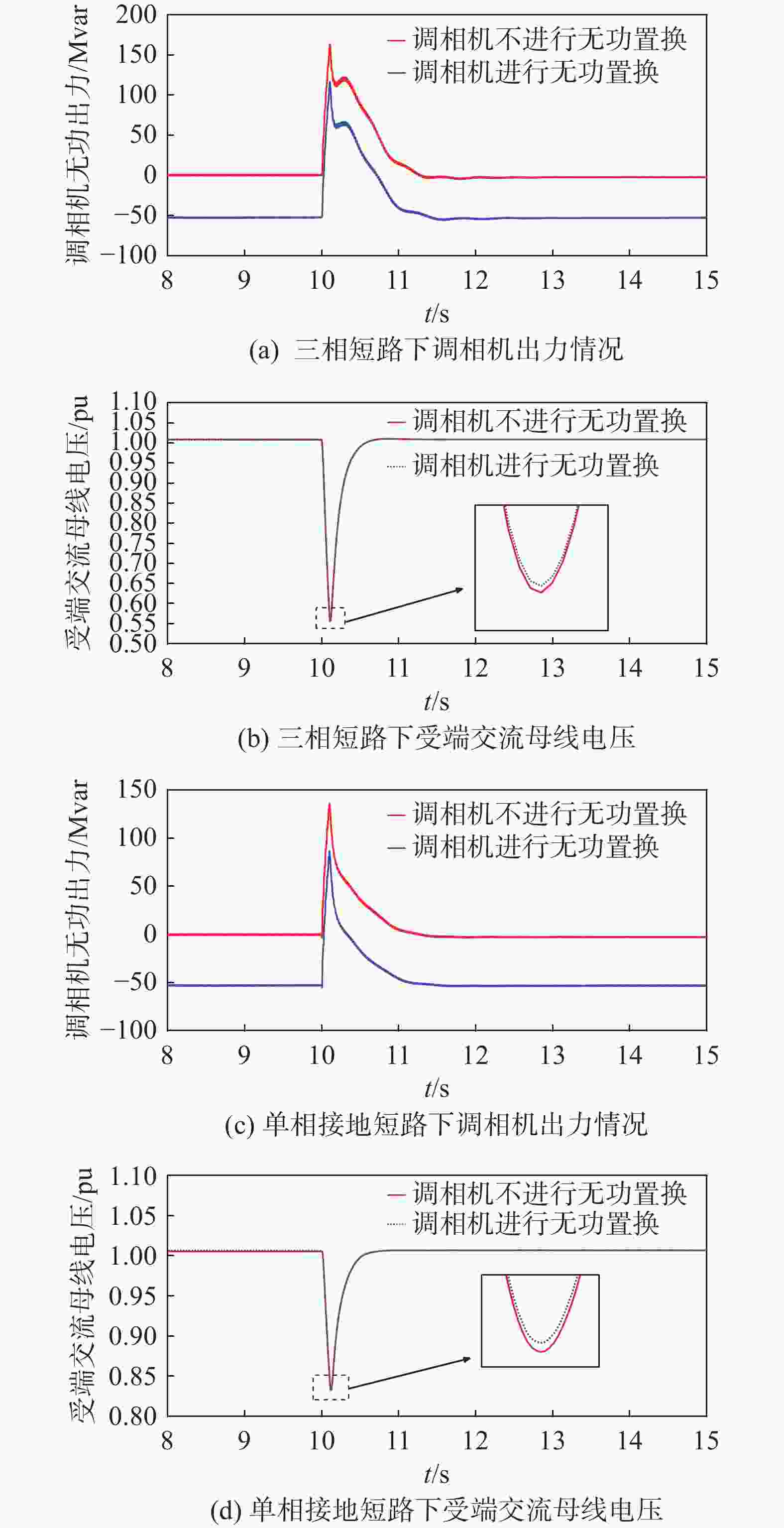
Figure 7. The output power of synchronous condenser and the AC bus voltage at the receiving end under different short-circuit ratios
由图7可知,文章所提的受端换流站无功补偿方案不影响调相机暂态下的无功支撑能力,且可以提升滞相运行能力,两种情况下电压稳定性相同,且提高故障下低电压的抑制能力。
随后验证受端换流站不同直流容量下交流滤波器投入情况如表2,方案一为交流滤波器单独进行无功补偿,方案二为引入调相机参与无功补偿。仿真模型设置受端换流站单组交流滤波器额定容量为220 Mvar。
直流容量/GW 调相机台数 方案一 方案二 2 1台 4组 5组 3 1台 7组 8组 4 2台 9组 10组 6 3台 15组 17组 8 4台 21组 23组 Table 2. Input of AC filter at the receiving converter station under different configuration schemes
由表2可知,受端换流站采用协调补偿方案后,可以增加交流滤波器投入组数,有利于受端稳定性。
4.1和4.2节仿真验证了送、受端换流站无功补偿方案的有效性,调相机参与稳态无功补偿可以优化送、受端换流站交流滤波器的配置方案。实际工程中,换流站通常会配置多种不同容量的滤波器,送、受端换流站无功补偿方案能够进一步得到优化。
-
为验证双层无功调整策略的有效性,先确定在PSCAD模型中无功补偿的配置策略:送端换流站单组交流滤波器额定容量为140 Mvar,死区值为65%(91 Mvar),并根据死区值设置稳态运行下调相机出力为120 Mvar,根据送端换流站单组交流滤波器容量设计调相机稳态出力范围为0~260 Mvar,即稳态下在120 Mvar基础可再置换一组交流滤波器。同时,在第一层无功调整结束后调相机可短时运行范围为−50 Mvar~300 Mvar。
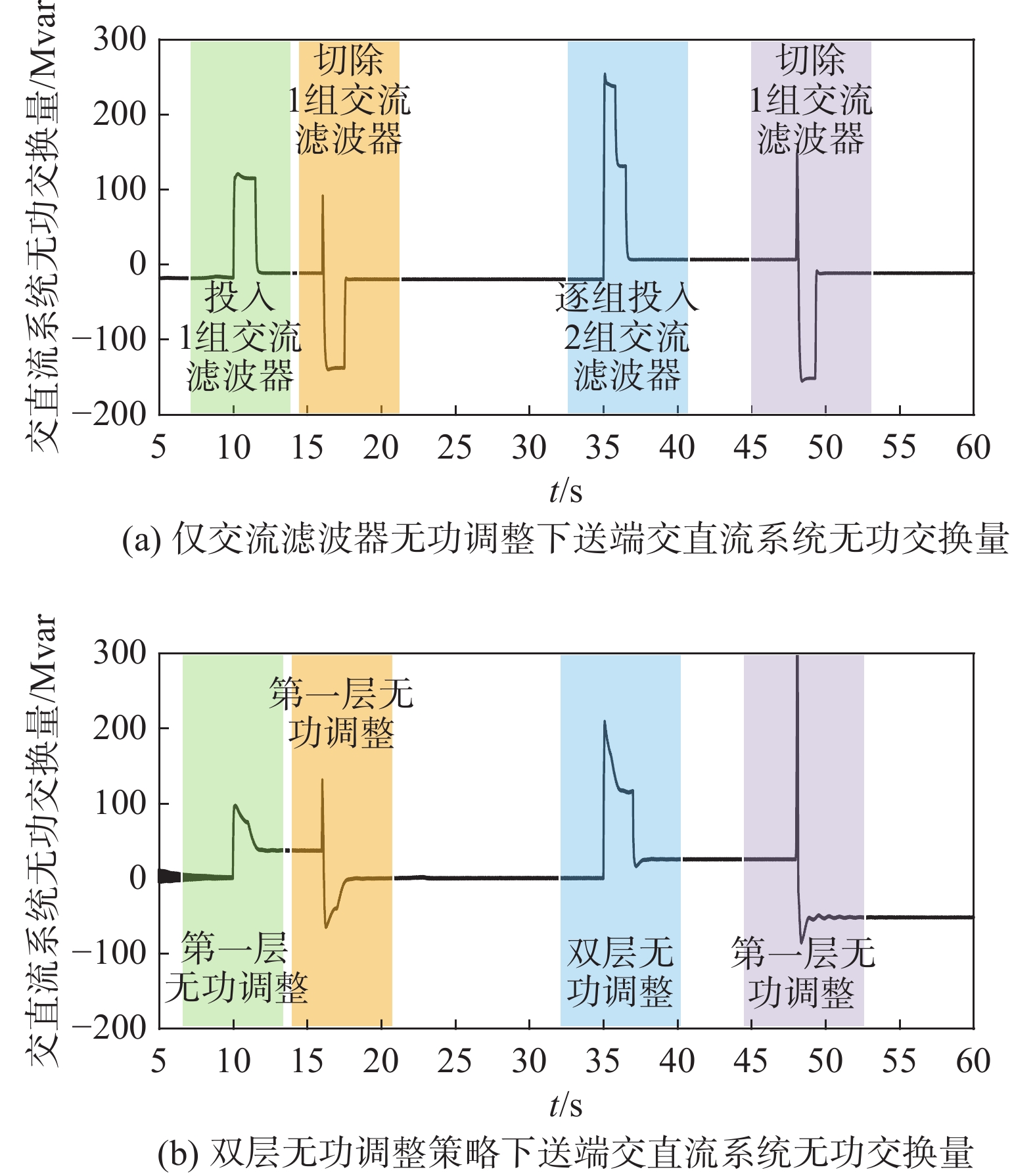
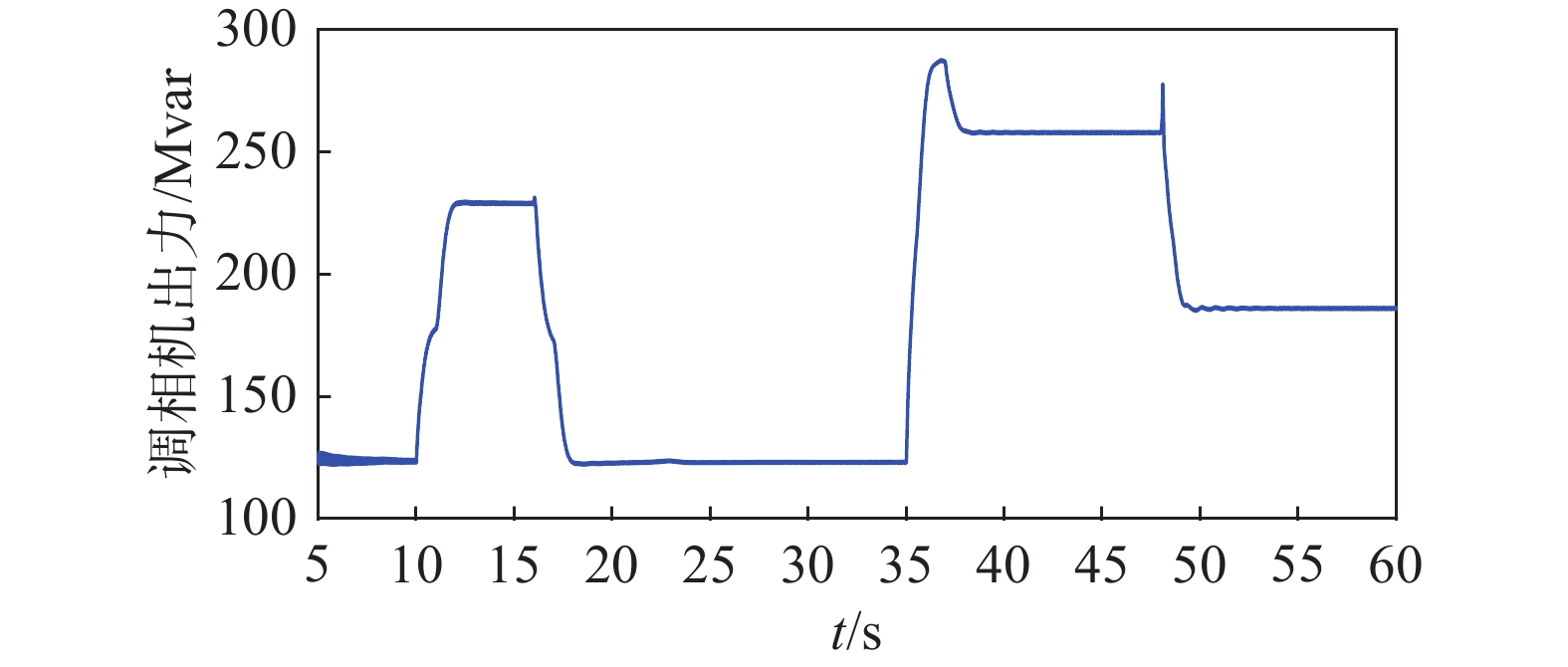
在PSCAD建立的电磁暂态模型中分别对交流滤波器单独进行无功调整和双层无功调整策略进行验证分析,送端换流站在10 s、16 s、35 s、48 s分别发生无功变化并进行无功调整。图8为两种无功调整策略下的送端交直流系统间无功交换情况,图9为双层无功调整策略下调相机无功出力情况。
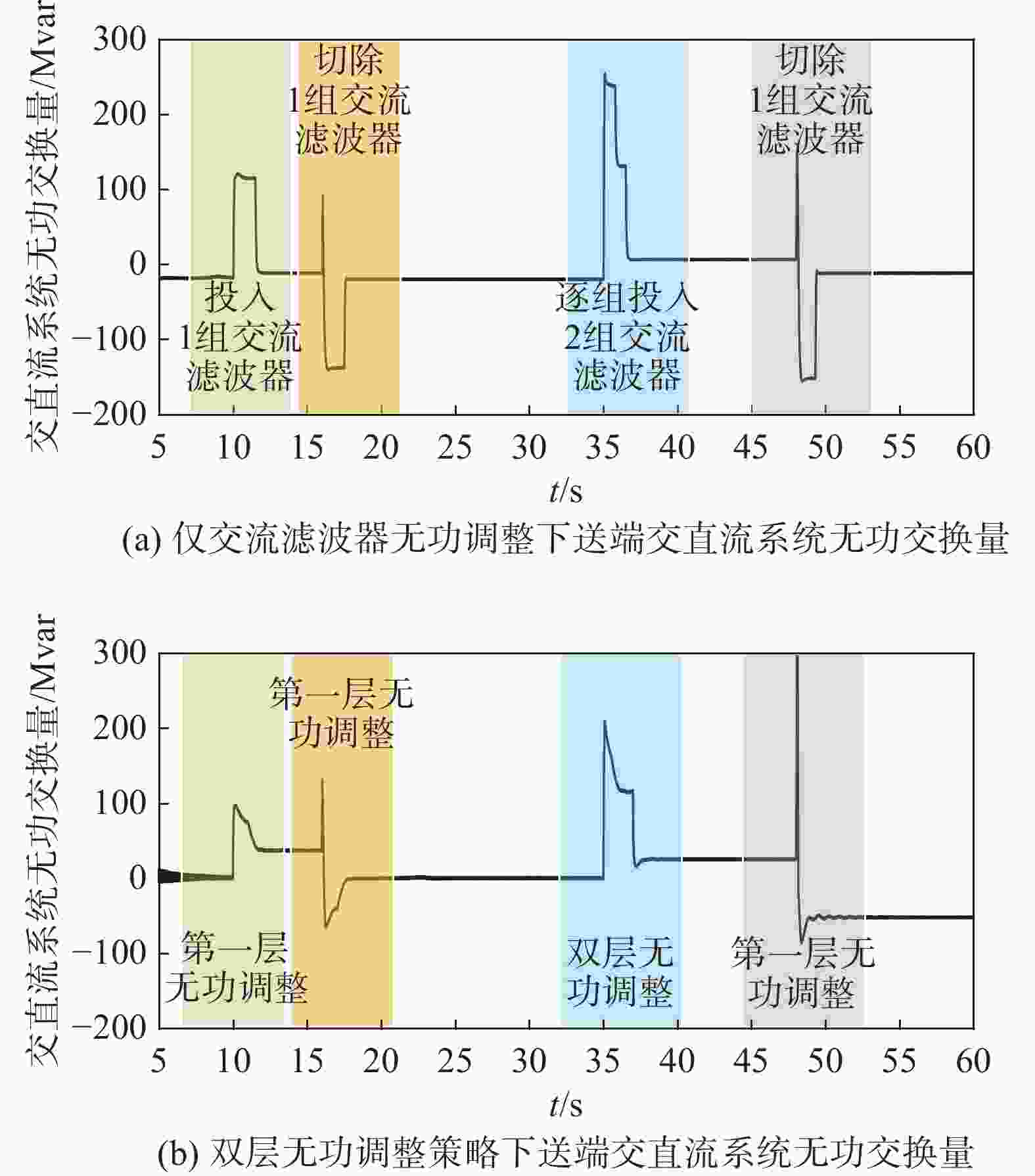
Figure 8. AC-DC system reactive power exchange at the sending end under different reactive power regulation strategies

Figure 9. Power output of synchronous condenser under double-layer reactive power adjustment strategy
由图8可知,仅由交流滤波器独立承担无功调整任务时,交流滤波器在10 s、16 s、48 s分别进行1 次投切,在35 s进行2次投切,整个仿真过程共发生5次交流滤波器的投切。在双层无功调整策略下,交流滤波器仅在35 s进行1次投切,其余无功调整过程均由调相机承担,由图9可知,该过程中调相机出力情况预设符合要求。上述送端换流站内仿真结果说明,在相比于调相机单独进行无功调整,双层无功调整策略能有效减少送端换流站交流滤波器投切次数,同时,相比于交流滤波器阶梯式出力,调相机在无功调整过程中平滑出力,有利于系统稳定性。
-
文章归纳了目前LCC-HVDC换流站调相机与交流滤波器的特性与应用范围,提出了调相机与交流滤波器共同参与换流站无功补偿的补偿方案和双层无功调整策略,并进行仿真分析。结果表明:
1)在送端换流站,调相机滞相运行,动态特性不受影响,可以增加暂态过电压的抑制能力。在受端换流站,调相机进相运行,暂态下响应速度不受影响,且可以提高无功支撑能力。
2)送端换流站引入调相机参与无功补偿,对交流滤波器进行无功置换,可以减少交流滤波器的投入组数,提高换流站运行的经济性。
3)双层无功调整策略可以减少换流站交流滤波器的投切次数,延长交流滤波器的使用寿命。
LCC-HVDC Converter Station Reactive Power Optimization and Two-Layer Coordination Strategy Research Based on Synchronous Sondenser
doi: 10.16516/j.gedi.issn2095-8676.2023.05.004
- Received Date: 2022-12-08
- Rev Recd Date: 2023-08-24
- Available Online: 2023-09-06
- Publish Date: 2023-09-10
-
Key words:
- converter station /
- HVDC /
- synchronous condenser /
- AC filter /
- reactive power compensation
Abstract:
| Citation: | ZHANG Dongqing, XU Lingling, LI Yanlong, ZHANG Guohua. LCC-HVDC Converter Station Reactive Power Optimization and Two-Layer Coordination Strategy Research Based on Synchronous Sondenser[J]. SOUTHERN ENERGY CONSTRUCTION, 2023, 10(5): 24-33. doi: 10.16516/j.gedi.issn2095-8676.2023.05.004 |








































 DownLoad:
DownLoad: