-
电力设施系统由输电塔、绝缘子串、高压输电线、保护金具、塔臂等结构组成,其中高压输电线是电力设施系统的重要组成部分[1]。作为国家经济建设的生命线工程,输电线路的正常运行保证了国家经济的稳定发展[2]。然而,舞动对于输电线路的安全运行最具破坏性,详见图1。高压输电线是电力设施系统的重要组成部分,出现故障会严重影响人民的日常生活和工作,而舞动是输电线路安全运行的最大威胁因素。因此,分析舞动发生的原因,进而开发防舞、抑舞技术是一项具有重要现实意义的课题。目前,我国电网的建设得到了国家财政的大力扶持,已经成为世界上规模最大的电网之一[1]。遗憾的是,随着恶劣气象、灾害的频繁出现,我国电网遭受舞动破坏的概率以及破坏程度都急剧上升,几乎每年都会发生大范围的舞动事件,带来了沉重的经济损失和严重的社会影响[3-4]。
输电线路系统防灾、减灾性能的评估及提高是多学科交叉的复杂工程,舞动对电网的影响分析涉及到力学、数学、电学和材料学等多个学科[3-4]。目前,虽然取得了不少科研成果,保证了电网的安全运行,但电网规模越来越大,分裂导线结构越来越多,安全可靠性要求越来越高,电网所处地区的地形、气象条件也变得更加复杂,舞动的发生概率增加。
文章基于近几十年来输电线路弯曲刚度、气动力系数、数值仿真、舞动方程的理论求解等方面的研究现状,总结了现有研究的优点、缺点,并分析了输电线路舞动相关课题的发展趋势,为国内及国外输电线路舞动灾害的防治和运行维护提供了参考。
-
覆冰输电线的舞动是一个相当复杂的课题,其复杂性体现在:(1)它属于流-固耦合振动;(2)气象、地区、结构参数、人工制造等造成的随机性;(3)输电线的几何非线性特征以及塔线耦合效应。因为输电线的档距远大于其直径,所以输电线属于柔性索单元结构。近几十年来,国内外学者基于索单元做了大量与输电线舞动有关的研究,取得了丰富的研究成果。目前针对单档输电线的非线性振动研究较多,关于多档输电线振动的研究成果还较少。Irvine[4]建立了索单元结构的经典理论,对悬索结构的静力学、线性和非线性动力学行为进行了研究,给出了索单元结构任意模态之间可能发生耦合共振的条件,并提出了重要的Irvine系数。该参数是和几何参数有关的重要参数,对索单元结构的动力学特征分析起着至关重要的作用,其相关的研究成果已经被广泛运用于学术界、工业界中。
针对覆冰输电线的非线性舞动特征研究,为了简化理论模型及方便求解理论模型对应的舞动方程,大部分科技学者们都选择忽略弯曲刚度对覆冰输电导线舞动特征的影响。然而,在实际工程中,输电导线的弯曲刚度随着其直径的增加而增加,且弯曲刚度会影响输电导线的舞动频率,进而可能导致输电导线的舞动特征发生改变。因此基于索单元结构来研究特大直径输电导线的舞动特征时忽略其弯曲刚度可能并不合理。基于这一“出发点”,部分学者们重新推导了单档输电导线的舞动方程,重点评估了弯曲刚度对输电导线舞动特征的影响。
赵跃宇等[5]基于哈密顿变分原理推导了索单元结构考虑弯曲刚度影响的三自由度耦合振动方程,结合边界条件和降维法将无穷维自由度系统转变为有限维自由度系统,利用摄动法分析了索单元结构可能存在的内共振模式,通过MATLAB研究了弯曲刚度对索单元结构内共振的影响程度。结果表明:弯曲刚度会使得索单元结构的固有频率增大,进而使得索单元结构发生内共振的条件向左偏移;受弯曲刚度的影响,索单元结构内共振条件下的幅值和拍频的大小都将增大。赵跃宇等[6]基于伽辽金法研究了弯曲刚度对索单元结构面内、面外的一阶频率及高阶频率的影响。其研究结果表明:弯曲刚度对面外频率的影响较大,弯曲刚度对面内频率的影响较小,且弯曲刚度对频率的影响随着模态函数阶次的增加而增大。该研究成果对实际工程有一定的指导价值。
肖一等[7-8]在已有文献的研究基础上,考虑了弯曲刚度对索单元结构静力构型的影响,首先推导了两端固结悬索的面内自由振动解析解,接着推导了两端铰接悬索的面内自由振动解析解,对比了两种边界条件下悬索的动力学行为,并修改了已有文献的研究结论。学者肖一在建立悬索自由振动理论模型时,重点考虑了弯曲刚度对悬索结构振动特性的影响,因此其研究成果在理论上会更为准确。Wu等[9]也推导了考虑弯曲刚度影响的索单元面内外耦合振动的新方程,修正了Irvine提出的索单元面内外耦合振动方程,讨论了新振动方程的适用范围,接着采用有限差分法验证了新振动方程的正确性。因此其研究成果通过修正既有方程并引入弯曲刚度影响,可以更准确地预测结构的振动特性和响应。这对于工程设计、结构优化等方面都具有重要意义。
Yan等[10]建立了考虑弯曲刚度影响的节点六自由度索单元有限元方程,并采用Newton-Raphson迭代法求解了该有限元方程,最后通过数值算例进行了结果分析。算例表明:当覆冰输电导线振动时,导线的弯曲刚度对扭转角影响最为显著。Yan等[11-12]接着进一步考虑了弯曲刚度对输电导线振动性质的影响。算例分析表明:忽略弯曲刚度会使得导线振动时的幅值降低,这一点与文献[5]的研究结果吻合。其研究结果表明忽略弯曲刚度的影响,可能会低估导线的振幅,从而导致未能正确地评估其疲劳寿命或者出现意外事故。因此引入弯曲刚度考虑可以更准确地预测导线振动,从而更好地保障电力系统的稳定性和可靠性。吕建根等[13]在文献[5]的基础上进一步推导了考虑弯曲刚度效应的索单元面内、面外内共振的幅-频响应方程,结合多尺度法和数值法系统地研究了索单元的1∶1和2∶1的内共振模式,获得了较有意义的结论。接着,吕建根等[14]建立了索-梁耦合简化模型,进一步研究了索-梁系统中索单元的非线性响应。算例分析表明:考虑弯曲刚度后,索单元结构的长度对索单元面内基频的影响较大;对于长度较短的索,应考虑弯曲刚度;弯曲刚度会使索单元的幅-频响应曲线、激-频响应曲线向左偏移,偏移的幅度取决于弯曲刚度的大小。该研究成果为后续进一步确定应考虑弯曲刚度的索单元结构长度的范围提供了依据。刘小会等[15]提出了两种不同的动张力计算公式,并研究了这两种计算公式下弯曲刚度对索单元1∶1、2∶1内共振的影响。接着,刘小会等[16-17]在其自身研究的基础上进一步考虑了索单元的气动效应,建立了覆冰索振动的拟静态模型,系统地研究了弯曲刚度对覆冰索振动特征的影响。算例分析表明:对于档距大于300 m的索单元结构,弯曲刚度对相位、幅值的影响较小,对于档距小于300 m的索单元结构,不能忽略弯曲刚度的影响。该研究结果给出了在保证计算效率的同时,尽可能地提高模拟结果精度而考虑弯曲刚度的索单元结构长度的一定范围。该研究成果对于后续类似的模拟分析具有一定的指导价值。
Younespour等[18]为了评估索单元的弯曲刚度对索网平面内动力响应的影响,对现有的双索网分析模型进行了改进,导出了一组闭式解,清楚地揭示了索单元弯曲刚度对两种不同结构索网模态响应的影响。结果表明:索单元的弯曲刚度会通过增加索网的模态频率来影响索网的所有模态,其中对高阶整体模态和局部模态的影响更为显著。如果忽略不计,网络基频可能会出现高达7.1%的误差。此外,索单元的弯曲刚度对局部模态的影响大于对整体模态的影响。其研究结果表明忽略弯曲刚度的影响,可能会产生较大的网络基频误差,从而影响结构的振动特性和响应。因此应引入弯曲刚度考虑以保证计算结果的准确性和可靠性。
-
气动力系数是覆冰分裂导线舞动特征分析与防舞、抑舞技术开发的关键参数,国内外学者在这方面皆做了许多研究。分析覆冰导线的气动特性之前,需了解覆冰导线的分裂类型,常见的类型有单分裂、双分裂、四分裂、六分裂、八分裂,图2[19]给出了双分裂、四分裂的图片。针对覆冰单导线、多分裂导线气动力系数的获得,需建立不同的试验、仿真模型,并采用合适的研究方法,就目前而言,学术界、工业界普遍采用的研究方法有3种:(1)现场监测;(2)开展导线节段模型的风洞试验;(3)利用流体计算软件进行仿真、模拟。

Figure 2. Types of transmission line bundle[19]
在现场监测方面,国内学者[20-22]针对湖北中山口地区覆冰导线的舞动测得了一系列气动力系数,部分气动力系数对于实际工程而言有着十分宝贵的参考价值。
在风洞试验方面,李万平等[23]通过风洞试验测试了不同工况下覆冰单导线和双分裂导线的气动力系数,并研究了覆冰类型、尾流效应、冰厚以及风速对气动力系数的影响,其试验成果对防舞、抑舞技术的开发起到了参考、借鉴的作用。同时,李万平等[24-25]还进行了覆冰导线的拟静态特性试验和动态特性试验,试验得知拟静态特性试验能给出动态特性试验的主要特征。张宏雁等[26-28]在文献[23]的基础上进一步制作覆冰四分裂导线节段模型,通过风洞试验获得了不同覆冰冰型、覆冰厚度、平均风速下导线的静态气动力系数。楼文娟等[19]选取不同厚度的分裂导线与单导线进行了风洞试验,并分析了厚度对气动力系数的影响,结果表明:厚度对气动升力系数和气动阻力系数有着明显的影响。接着,楼文娟等[29]针对覆冰六分裂导线的气动力系数不完善问题进行了覆冰六分裂导线的风洞试验,分别基于试验实测和舞动非线性计算判定了实际输电线路的起舞风速。Cai等[30]通过风洞试验测量了覆冰八分裂导线模型各子导线的气动力系数,试验结果得知:子导线之间存在明显的尾流效应,因此八根子导线的气动力系数存在较明显差异,尤其是当子导线处于上风子导线的尾流区时,作用于其上的阻力会明显下降,这对覆冰八分裂导线舞动特性及防舞的后续研究有一定的参考意义。风洞实验可以提供真实物理的模型,可以模拟实际风场下导线的振动情况。通过风洞实验可以获得更准确的数据和更全面的信息,可以更好地研究导线舞动特性,为输电线路的设计和运行提供科学依据,因此利用风洞实验研究输电导线舞动特性具有非常重要的意义。
在软件仿真方面,彭家宁等[31]建立了覆冰单导线的空气流场二维CFD(Computational Fluid Dynamics,计算流体动力学 )模型,结合风洞试验验证了CFD数值模拟方法的准确度和可靠性。王琼等[32]采用流体计算软件对影响覆冰导线气动力系数的主要因素进行了详细的研究,接着采用风洞试验再一次对影响气动力系数的因素进行了研究,对比两种方法所得结果发现:虽然两种方法所得结果存在一定的误差,但是误差在允许的范围内,即可采用价格低廉的流体计算软件来分析影响覆冰导线气动力系数的关键因素以达到降低工程预算、节约成本的目的。吕翼等[33]采用有限体积法和SIMPLEC算法,对风吹过平行布置的覆冰三分裂导线的气动力特性进行CFD数值模拟。计算结果表明:新月形覆冰三分裂导线比扇形覆冰三分裂导线舞动的风攻角范围大,但前者的舞动幅值小于后者;分裂导线中处于尾流区的子导线的气动力系数均小于迎风面子导线的气动力系数,且扇形覆冰导线比新月形覆冰导线更为显著。相对于风洞实验而言软件仿真可以快速地模拟不同条件下的导线振动情况,可以进行大量的参数分析和优化设计。软件仿真可以快速地评估不同导线类型、张力、风向和风速等因素对导线舞动特性的影响,可以为实验设计提供重要的参考。
-
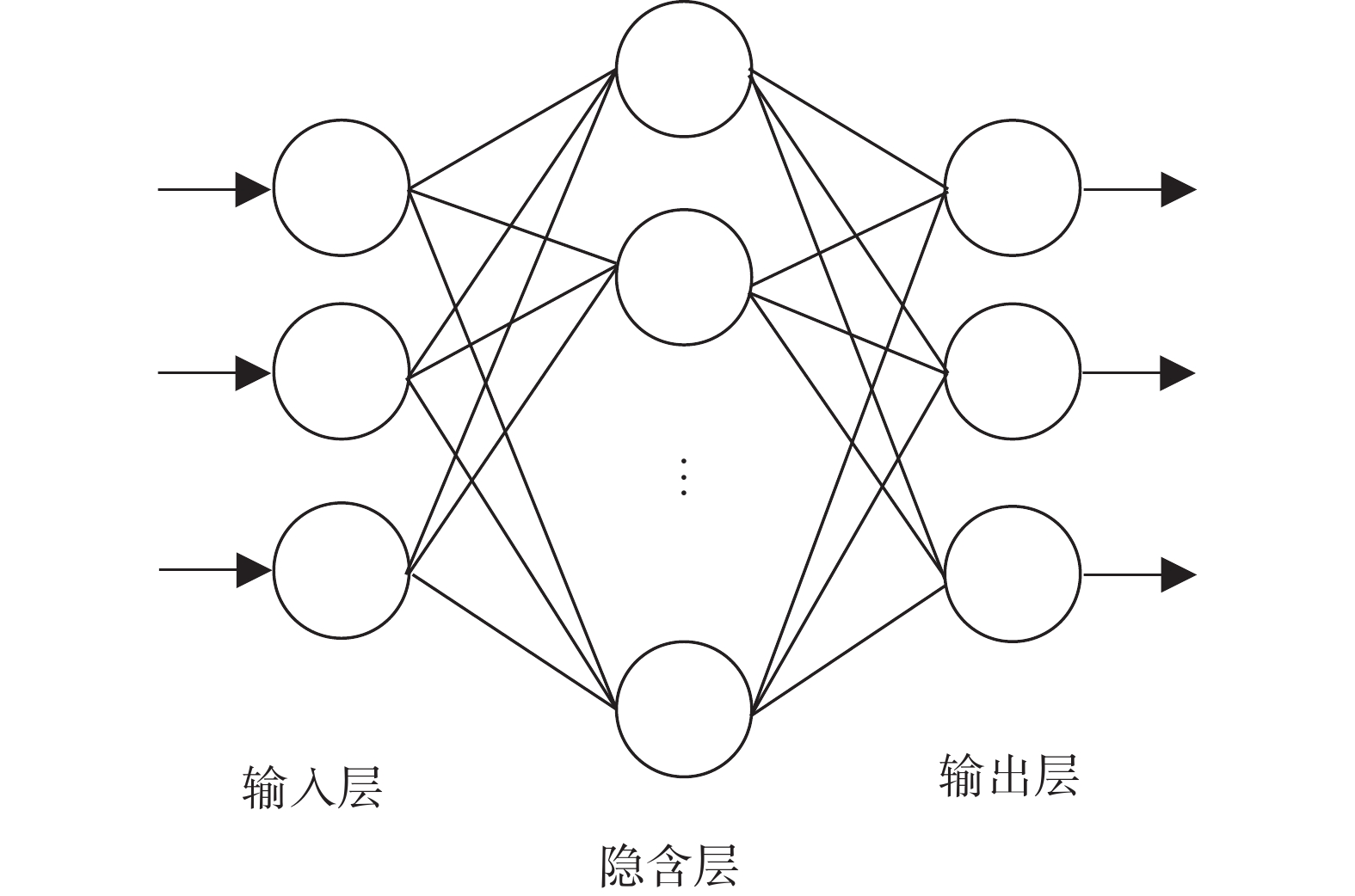
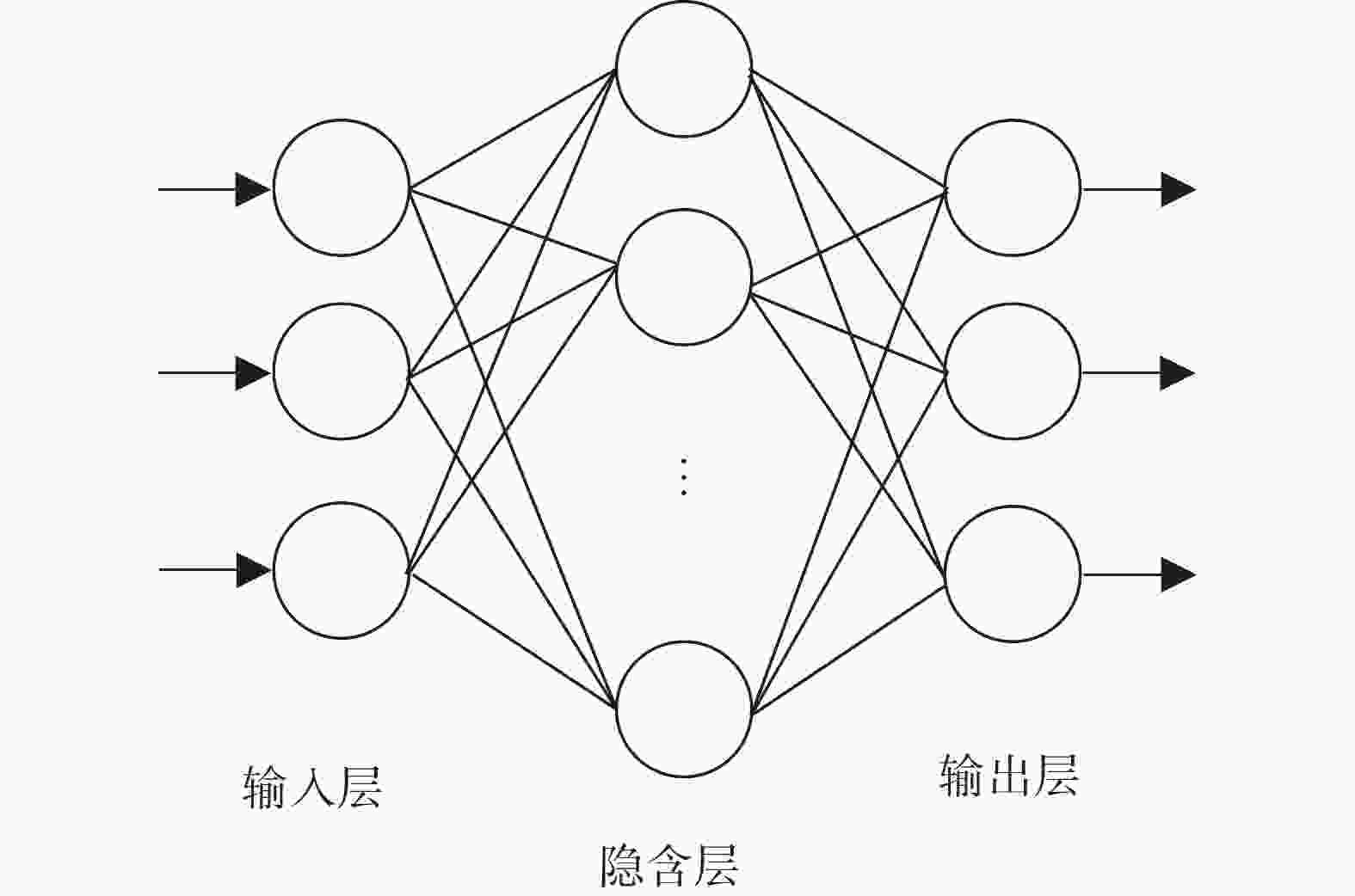
近年来,随着计算机技术的快速发展,神经网络在多个不同领域的应用研究受到了科技学者们的密切关注。简单来讲,人工神经网络是模拟生物神经网络进行信息处理的一种数学模型,具有广泛的应用前景,得到了国家财政的大力支持。目前,在人工神经网络的实际应用中,几乎大部分模型都是采用反向传播算法(Backpropagation Algorithm,BP),学者们将采用BP算法的人工神经网络定义为BP神经网络[34]。BP神经网络的网络结构是分层排列的,且每一层神经元的输出值仅与下一层相连接,即所谓的前馈式网络结构,BP神经网络由输入层、隐含层、输出层3层网络构成,详见图3。图3中的输入层通常表示影响研究对象的因素;输出层则为研究对象的预测值;隐含层的作用则是调节预测值与真实值的差值,一般来讲隐含层越多,该差值越小,但计算量就会成倍增加,因此隐含层的数目需根据实际情况而设置[35-36]。BP神经网络的功能较多,大众熟知的有预测、识别、控制、诊断等功能,目前在预测领域的研究成果较多,部分学者基于BP神经网络对特定研究对象的气动力系数进行了预测、识别。
国内早期阶段,学者李林[37]在其硕士论文中简单描述了BP神经网络的计算法则,接着采用BP神经网络识别了桥梁断面的气动力系数,并分析了数据处理方式、隐含层数目等参数对预测结果的敏感性,预测结果验证了基于BP神经网络识别桥梁断面的气动力系数的可行性。2008年,Chen等[38]建立了BP神经网络预测理想薄板的气动力系数模型,并比较了多种参数对预测结果的影响,最终证明了BP神经网络在预测领域的科学性。2010年,黄继鸿等[39]建立了BP神经网络的翼型空气动力预测模型,接着对该模型的升力系数和阻力系数进行预测,并与风洞试验数据进行了对比分析,最终验证了BP神经网络预测翼型空气动力系数的可行性。2019年,陈讷郁等[40]在文献[37]的基础上进一步改进了BP学习算法,接着根据风洞试验所得的气动力系数预测了相似桥梁断面的气动系数,其研究成果具有十分重要的现实意义。现阶段利用BP神经网络预测气动力系数可以提高其预测精度:利用BP神经网络可以通过对大量实验和模拟数据的学习,提高预测气动力系数的精度和准确性;可以减少实验和计算成本:传统的气动力系数预测方法需要进行大量的实验和计算,成本较高且耗时,利用BP神经网络可以通过对已有数据的学习,快速地进行气动力系数预测,减少实验和计算成本;可以优化设计方案:利用BP神经网络可以对不同气动参数和结构参数进行优化设计,以实现更好的气动力性能。
-
考虑到输电线路模型的复杂性,最初的输电线舞动特征的分析对象主要是覆冰单导线。例如:张栋梁等[41]建立了三个平动自由度和一个扭转自由度的偏心耦合覆冰单导线非线性有限元模型,将相邻档导线和绝缘子串等效为弹簧,研究了覆冰单导线的舞动特征。王昕等[42]基于三节点等参单元建立了覆冰单导线的有限元模型,同时在文献[41]的基础上考虑了湍流的影响,数值结果表明:以弹簧作为单导线舞动的边界条件,弹簧刚度对舞动幅值有明显的影响。胡霁等[43]采用数值方法比较了单档和三档模型计算结果的差异,研究结果表明:覆冰单导线舞动时相邻档导线对舞动档导线的舞动幅值影响较为明显。
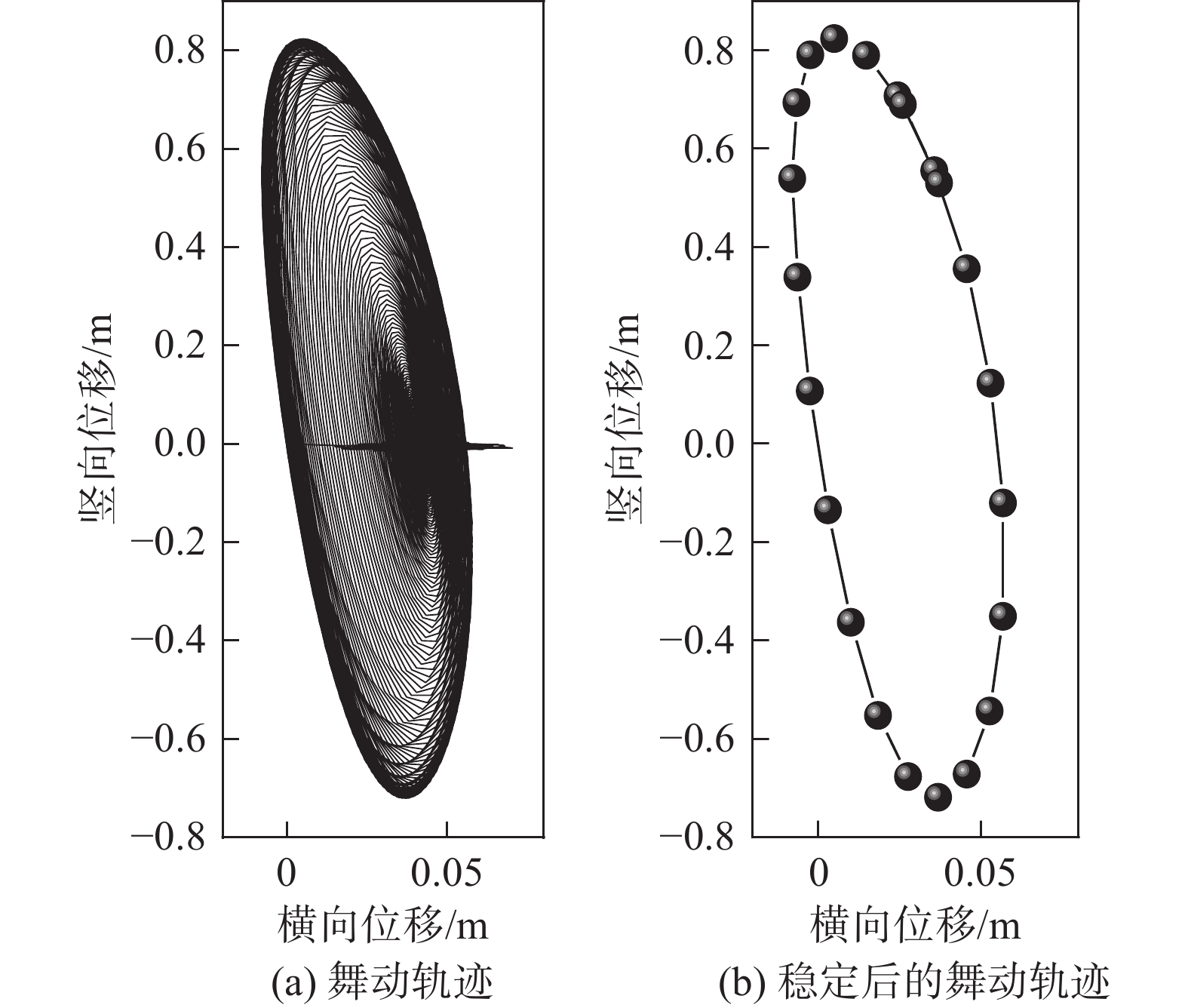
考虑到覆冰的影响,覆冰单导线的舞动通常表现竖向-横向-扭转三自由度的偏心耦合振动,导线的舞动轨迹通常为垂直走向的椭圆形。Liu等[44]首先通过风洞试验得到了覆冰单导线的气动力参数,接着建立了覆冰单导线的有限元模型,对覆冰单导线的舞动特性进行了模拟,得到了导线中点的轨迹,如图4所示。另外,也有许多学者[45-49]采用类似的方法建立了覆冰单导线舞动的有限元模型,得到了单导线中点的舞动轨迹,他们的研究结果都表明:覆冰单导线中点的舞动轨迹可归纳为垂直走向的椭圆形。

Figure 4. Galloping track of the midpoint of single conductor covered with ice (Liu Xiaohui model)[44]
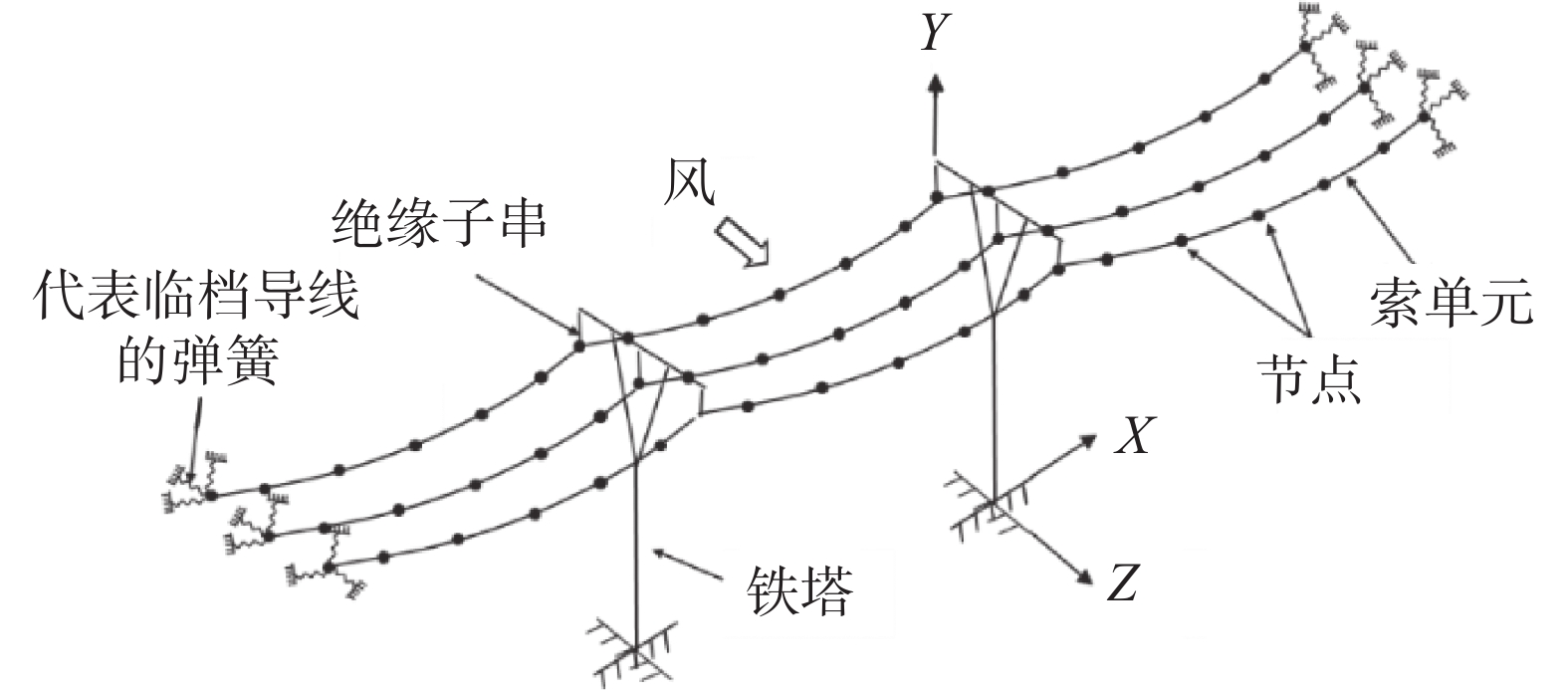
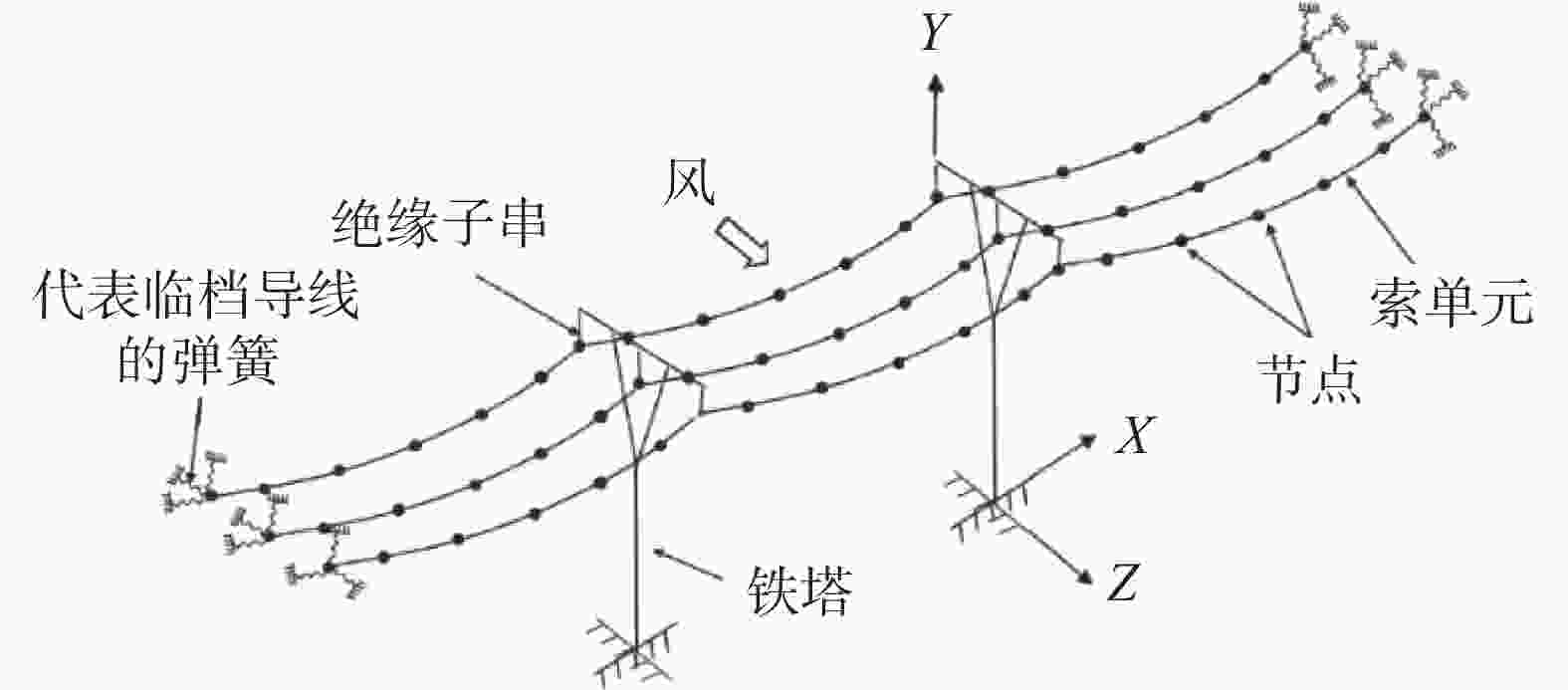
随着我国经济的飞速发展以及我国电力战略部署,越来越多的大跨越分裂导线结构被建立,且分裂导线通过间隔棒衔接为一个整体从而导致分裂导线的扭转刚度较大,最易诱发舞动,因此分析覆冰分裂导线的舞动特性是必然趋势。利用现场调研、风洞试验或者数值模拟得到覆冰分裂导线的气动力系数,接着基于气动力系数建立有限元模型(图5为多档导线有限元模型简图),进而研究覆冰分裂导线的舞动特征,达到开发防舞、抑舞技术的目的,已经是一套比较完善的算法。
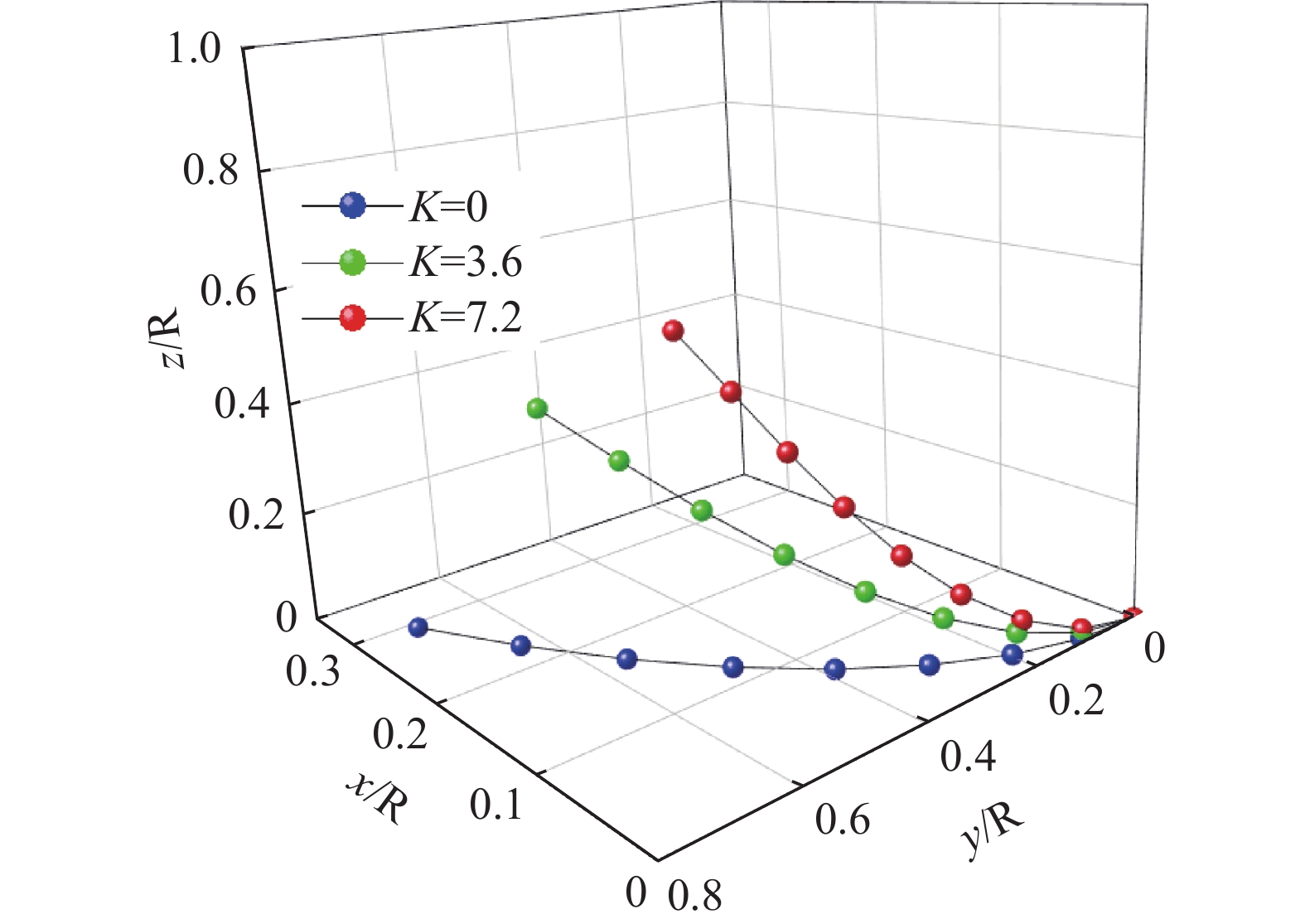
覆冰分裂导线的舞动是一种自激振动,数值模拟花费时间较长。为了能够更高效地模拟覆冰分裂导线的舞动,导线通常采用具有扭转自由度的三节点索单元模拟,间隔棒通常采用梁单元模拟,输电塔采用梁和杆的混合单元模拟,学者刘小会等[50]开发了一类梁单元,该单元可用于模拟梁的大位移、大转动,且结果良好,如图6所示。
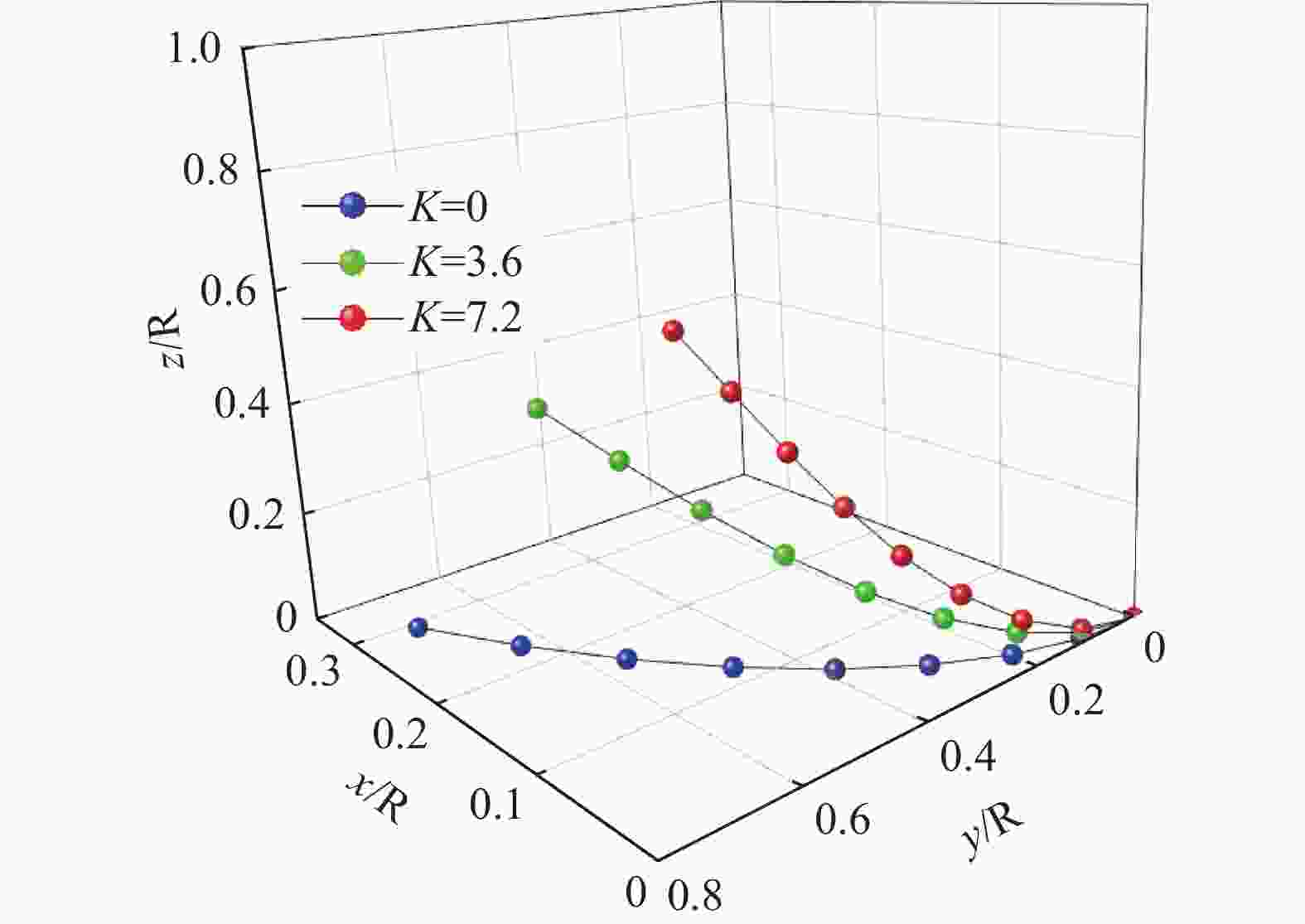
Figure 6. Spatial bending beam model[50]
刘小会等[51]基于其自身开发的梁单元,采用具有三个平动自由度和一个扭转自由度的三节点等参单元离散覆冰导线,用欧拉梁单元离散间隔棒,编制了相应的计算程序,通过算例验证了方法和程序的正确性。刘小会等[52]进一步利用由风洞实验获得的覆冰四分裂导线的空气动力系数,模拟研究具有不同档距的覆冰四分裂线路的舞动,为架空输电线路的设计提供了参考价值。覆冰输电导线的舞动是非线性振动问题,针对非线性振动问题的研究首选ABAQUS软件。严波等[53]基于ABAQUS软件的自定义单元施加气动力载荷,模拟了覆冰四分裂导线的起舞过程,最后对覆冰四分裂导线的舞动特征进行了系统的分析,同时研究了风速、档距、湍流等关键参数对舞动幅值的影响。覆冰输电导线的舞动同样是流-固耦合振动,针对流-固耦合振动问题的研究首选ANSYS软件。杨伦等[54]在文献[53]的基础上,通过ANSYS建立了覆冰四分裂导线的舞动模型,并考察了流场对导线舞动幅值的影响。向玲等[55-56]也通过ANSYS软件模拟了覆冰四分裂导线的气动特性、舞动特性,并采用风洞试验验证了其模拟结果的正确性。蔡萌琦等[57]结合风洞试验与ABAQUS用户子单元程序系统地研究了覆冰八分裂导线的气动特性、舞动特性。相较于传统实验方法而言,输电线数值模拟可以模拟多种工况,如风、温度、电荷等因素的作用下,输电线路的响应和振动情况;可以模拟多种输电线路的结构形式;可以大幅降低研究成本;可以模拟高风速、高温度等极端条件下输电线路的响应情况,避免了实验过程中可能出现的安全隐患。同时输电线数值模拟也存在一些缺点,如模型的准确性受限:输电线数值模拟的准确性受到模型的精度和参数的影响,因此需要对模型进行不断优化和验证;计算量大:输电线数值模拟需要进行大量的计算,因此需要高性能的计算机和软件支持;数据处理难度大:输电线数值模拟产生的数据量大,处理难度较大,需要专业的数据处理技术和工具。因此,在实际应用中需要综合考虑其优缺点,选择合适的方法进行研究。
-
关于覆冰输电线舞动发生的原因,不同学者提出了不同舞动机理,熟知的有:Den-Hartog[58]提出的竖向失稳机理;Nigol等[59-60]提出的竖向-扭转二自由度耦合的舞动机理;Yu等[61-62]提出的三自由度偏心耦合失稳机理。此外我国学者蔡廷湘[63]也提出了一种舞动机理。以上舞动机理皆能有效地解释覆冰输电线发生舞动的原因。基于舞动机理,国内外学者采用非线性振动方法对舞动这一特殊现象展开了大量的研究,较为普遍的方法有:(1)奇异摄动法;(2)多尺度法;(3)平均法;(4)增量谐波法;(5)同伦分析法。
蒋扇英等[64]基于松弛索振动理论建立了架空输电线非线性振动的理论模型,应用奇异摄动方法得到该模型的1次、2次、n次近似解析解,结果表明:随着近似次数的增加,解析解和数值解的误差逐次接近零,验证了奇异摄动法研究输电线振动特征的可行性。Luongo等[65-67]建立了输电线舞动的竖向-水平二自由度耦合振动模型,采用奇异摄动法分析了该耦合振动模型的稳定性,并推导了1∶1共振、1∶2共振以及非共振下舞动方程的近似解析解,又在此基础上进一步研究了舞动的连续分岔特征。该研究方法精度高,可以处理复杂的输电线舞动问题,可以针对不同的输电线舞动问题进行调整和优化。同时该方法也存在一些缺点,如计算量大,依赖于模型的准确性,难以处理非线性问题等。
李欣业等[68-69]基于竖向-扭转二自由度耦合模型,采用多尺度法分析了风速、档距等参数对覆冰导线舞动稳定性和舞动特性的影响。目前,针对覆冰导线混沌特性的研究还较少。基于此,侯磊等[70]结合文献[66]建立的二自由度覆冰导线舞动方程,进一步使用多尺度法系统地分析了1∶1、2∶1及3∶1内共振模式下覆冰导线的混沌特性和复杂的动力学行为。刘小会等[71]应用多尺度法分别求解了覆冰四分裂导线竖向-扭转二自由度耦合模型和竖向-横向-扭转三自由度舞动模型的位移响应,对比了两种模型位移响应的区别,发现扭转方向上的位移响应的差别最为明显。该研究方法具有高效性、适用性广、可以提供更多信息等优点,同时存在着计算量大、需要建立准确的多尺度模型、需要进行误差分析和纠正等缺点。
蔡君艳等[72]建立了覆冰四分裂导线竖向-横向-扭转的三自由度舞动模型,运用平均法获得了1∶1、3∶1共振情形下舞动幅值的解析解,并用数值法验证了解析解的正确性。郝淑英等[73]使用平均法分析了舞动幅值、张力等因素对覆冰导线舞动频率的影响。在文献[74]的基础上,刘小会等[75-76]首次考察了两种连续系统离散方法对舞动方程解的精度影响,首先使用多尺度法研究了覆冰导线的舞动特征,然后提出二自由度的平均法,并应用其研究覆冰导线的舞动特征,将两种方法所得结果进行对比,证明所提出的二自由度平均法的合理性。平均法具有计算简单、适用性广、误差较小等优点,同时具有精度较低、无法处理复杂情况、对模型要求较高等缺点。
晏致涛等[77]运用增量谐波平衡法推导了覆冰导线三自由度舞动模型的幅值解析解,结合实例分析了舞动方程中系数的取值对舞动幅值的影响程度,分析了1∶1和1∶2内共振模式下覆冰导线的舞动特征,并采用有限元对结论进行了验证。增量谐波法相对于多尺度法而言需要进行大量的计算,而多尺度法可以通过将问题分解成多个尺度的子问题来降低计算复杂度,从而提高计算效率;增量谐波法能对输电线舞动的微小变化进行高精度的计算和模拟,能够准确地预测输电线的振动情况但计算结果准确性要低于多尺度法;增量谐波法对模型的要求要略低于多尺度法。
吴钦宽[78]建立导线的非线性振动模型,利用同伦分析法得到了该模型的1次、2次和n次精度的近似解,并分析了精度对近似解的影响程度。赵珧冰等[79-80]利用法得到了无覆冰导线主共振下前两阶模态的近似解,分析了位移场与索力时程响应曲线,并与数值结果进行了对比分析,是一种基于同伦理论的数值计算方法,相对于其他方法而言同伦分析法能够对参数进行优化从而得到最优的输电线设计方案。同伦分析法还具有处理非线性问题、提供更多信息和高精度等优点。
-
1)针对弯曲刚度的研究:端部轴向激励荷载会使得索发生振动,共振时幅值将会大幅增加。然而,弯曲刚度会影响输电线的自振频率,进而使得共振发生的条件提前或延后。因此在研究覆冰输电线舞动特征时,不仅要考虑弯曲刚度的影响,还需考虑相邻档导线之间的相互作用。未来进行该研究时可以通过数值仿真和实验研究相结合的方法,建立覆冰输电线的数值模型,在考虑弯曲刚度、相邻档导线之间的相互作用、覆冰厚度等因素的情况下模拟输电线在不同工况下的舞动特征。通过探究在不同弯曲刚度、覆冰厚度、相邻档导线间距等因素对输电线舞动特征的影响,分析其机理。
2)针对气动力系数的研究:现场监测方法非常依赖于监测仪器的灵敏度、人力等,成本较高且耗时较长。数值仿真方法成本最低并能对风洞试验方法起到辅助作用,然而某些工况下其结果与实测结果误差较大。风洞试验可得到任意特定覆冰冰型导线模型的气动特性及其发生舞动的临界条件,并且能验证数值模拟的计算结果,但受实验室条件和模型的缩放比例影响,难以开展完整的风洞试验,得到理想的试验数据。未来进行该研究时可以采用风洞实验和数值仿真相结合的方法在保证数值模拟准确度的同时尽可能得到理想的实验数据。
3)针对BP神经网络预测气动力系数的研究:影响覆冰输电线气动力系数的因素较多,风速、湍流强度、高差、风攻角、档距、电磁力和间隔棒排布方式等关键参数都会影响覆冰导线的气动力系数。国内外基于神经网络预测覆冰导线气动力系数的研究成果还较少。未来利用BP神经网络预测气动力系数时可以通过采集大量数据以确定对气动力系数影响较大的因素,将数据预处理后建立一个合理的BP神经网络模型并对模型进行验证与优化。上述措施可以在利用BP神经网络预测气动力系数时,考虑到影响因素的复杂性和多样性,从而提高预测精度和可靠性。
4)针对数值模拟研究:舞动属于自激振动,能量积累需要很长的过程,而采用数值模拟方法时增量步通常较大,且计算耗时、收敛困难。除此之外,经过一次计算分析,数值模拟方法仅能获得某一特定参数下的覆冰导线舞动响应。未来针对数值模拟研究时可以采用简化的模型,降低模型的复杂度和计算量,从而提高数值模拟的效率;可以结合通过对不同参数的优化,提高模拟结果的准确性和可靠性;可以采用并行计算的方式,加速数值模拟的过程,缩短模拟时间。上述措施可以在未来开展相关研究时提高模拟的效率和准确性,更加全面地了解覆冰导线的舞动特性。
5)针对理论方法的研究:多档覆冰输电导线结构的理论建模、分析方法比单档覆冰输电导线结构更复杂,复杂的多档覆冰输电导线舞动分析方法涉及到高维非线性动力学系统的降维、全局分岔、周期解分岔理论及混沌等理论,是当前非线性科学研究的前沿课题之一。未来开展复杂的多档覆冰输电导线舞动分析时可以结合新的非线性动力学理论,建立更加精确的数学模型,提高输电线舞动分析的准确性;可以基于深度学习的数据驱动计算,提高计算效率和精度;可以结合智能化技术,对输电线舞动的大规模数据进行分析和建模,提高研究效率和准确性。上述措施可以提高输电线舞动分析的预测和控制能力。
Research Progress of Galloping of Overhead Iced Transmission Lines
doi: 10.16516/j.gedi.issn2095-8676.2023.05.015
- Received Date: 2023-04-03
- Accepted Date: 2023-07-10
- Rev Recd Date: 2023-05-31
- Available Online: 2023-08-24
- Publish Date: 2023-09-10
-
Key words:
- transmission lines galloping /
- galloping equation /
- bending stiffness /
- aerodynamic coefficient /
- numerical simulation
Abstract:
| Citation: | MIN Guangyun, ZHAO Xin, LIU Xiaohui. Research Progress of Galloping of Overhead Iced Transmission Lines[J]. SOUTHERN ENERGY CONSTRUCTION, 2023, 10(5): 116-128. doi: 10.16516/j.gedi.issn2095-8676.2023.05.015 |








 DownLoad:
DownLoad: