-
随着电力电子器件的发展,直流输电进入到了第三代新型直流输电,其基于全控型器件IGBT(Insulated-Gate Bipolar Transistor,绝缘栅双极晶体管)。采用全控型器件可以使换流器在四象限运行,实现有功无功解耦控制,因此特别适用于海上风电联网、无源网络供电、异步交流电网互联等。
传统的两电平或三电平电压源换流器(Voltage Source Converter,VSC)由于谐波含量大、容量低、电压等级低、器件串联动态均压并联均流等问题,发展受到了制约。2001年德国学者提出了模块化多电平换流器MMC(Modular Multilevel Converter,模块化多电平变流器)概念[1-3],西门子公司于2010年将其用于实际工程。近年来,基于MMC的工程越来越多,据不完全统计,目前已投运30项工程。国外工程集中在欧洲,主要将其用于海上风电的送出和电网互联。近年来国内已有南汇、厦门、舟山、鲁西、渝鄂、张北柔性直流电网、乌东德混合直流、三峡如东海风柔性直流、白鹤滩混合直流等工程。
文献[4-6]给出了MMC的基本数学关系和静态特性;文献[7]研究了采用PWM( Pulse Width Modulation,脉宽调制)方式的谐波特性;文献[8-10]对MMC的动态特性进行了建模研究;文献[11-13]研究了MMC联接弱交流电网的稳定运行区间;文献[14-16]开展了MMC孤岛送新能源场景下的控制研究;文献[17-18]就MMC处于直流电压控制下的稳定性开展了研究分析;文献[19-21]就MMC从电容电压控制出发开展的控制手段进行了研究。
近年来,对于MMC的研究主要集中于MMC与传统LCC(Line-Commuted Converter,换相换流器)直流的混合特性、主动故障隔离及故障清除策略、接入弱电网时的稳定性分析、新能源经柔性直流送出的稳定性分析、自适应强弱电网等方向。
其中对于柔性直流稳定性的分析成为重中之重,当前的分析手段是针对柔性直流系统的稳态工作点建立小信号模型,基于小信号模型得到柔性直流系统的阻抗特性,再根据柔性直流及外部电网的阻抗特性进行稳定性分析[22-24]。因此,对MMC稳态建模是稳定性分析的基石。
此外,高压大容量MMC换流器设备造价主要取决于IGBT器件及并联电容器的造价。当系统容量一定时,IGBT器件选型较为固定,并联电容器的大小选型的重要参考是子模块电容电压的波动。因此,对MMC的稳态工作点的精细化建模特别是模块电容电压分析具有重要意义。已发表的相关文献侧重点在于MMC内部环流产生原因及环流抑制的相关策略,文章则侧重电容能量变化规律,从子模块电容能量变化角度出发给出一种精细化数学建模,在推导出桥臂电容能量的波动公式前提下,深入研究了桥臂电容电压随时间、功率因数角、子模块电容大小的波动规律,根据电容电压的波动得到MMC谐波分布特性,并得出二次谐波的估算公式;在电容电压波动前提下,研究了桥臂子模块投入个数和模块电容电压随时间、功率因数的关系;最后对得到的规律进行了详细的仿真验证。
-
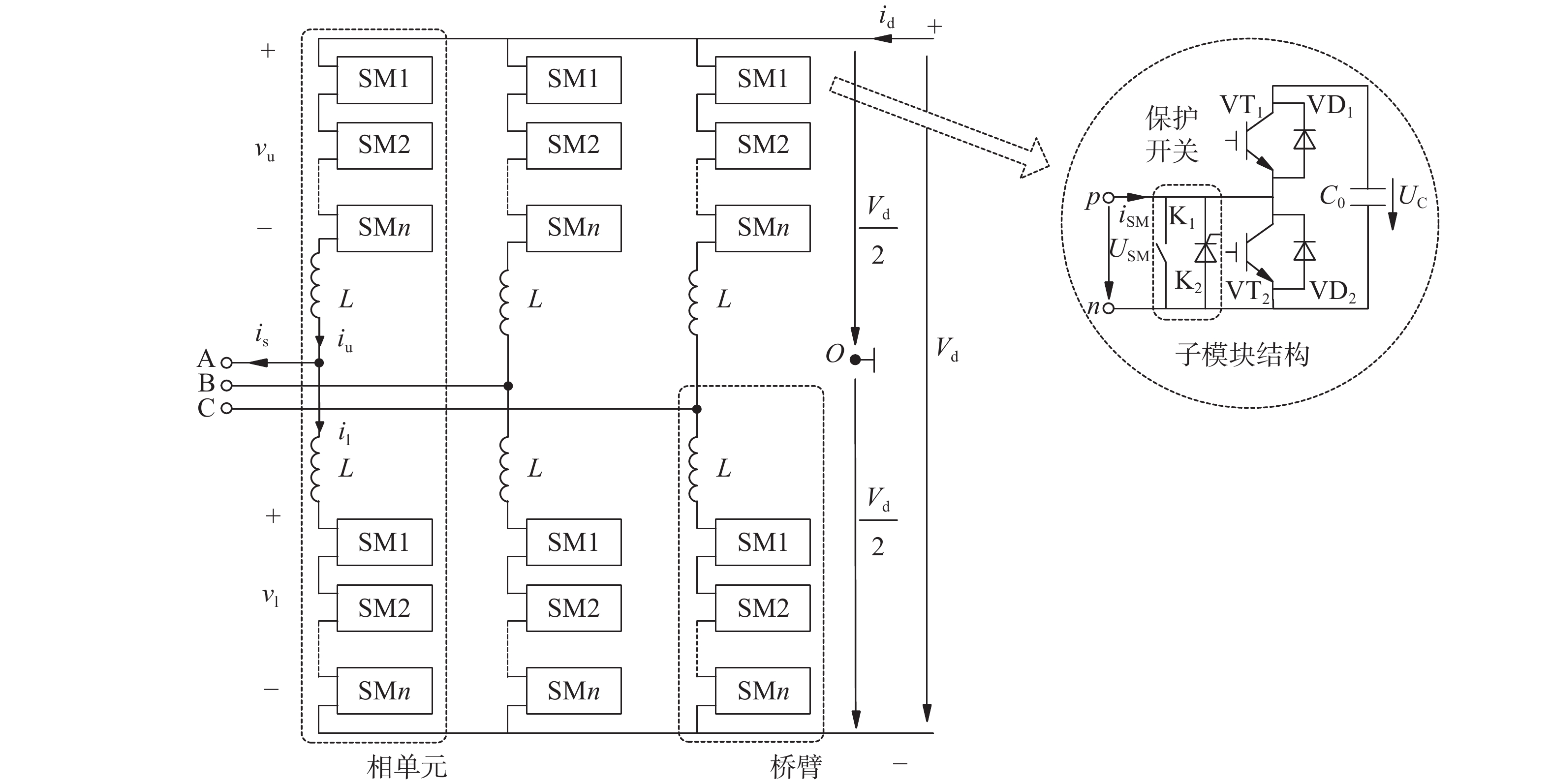
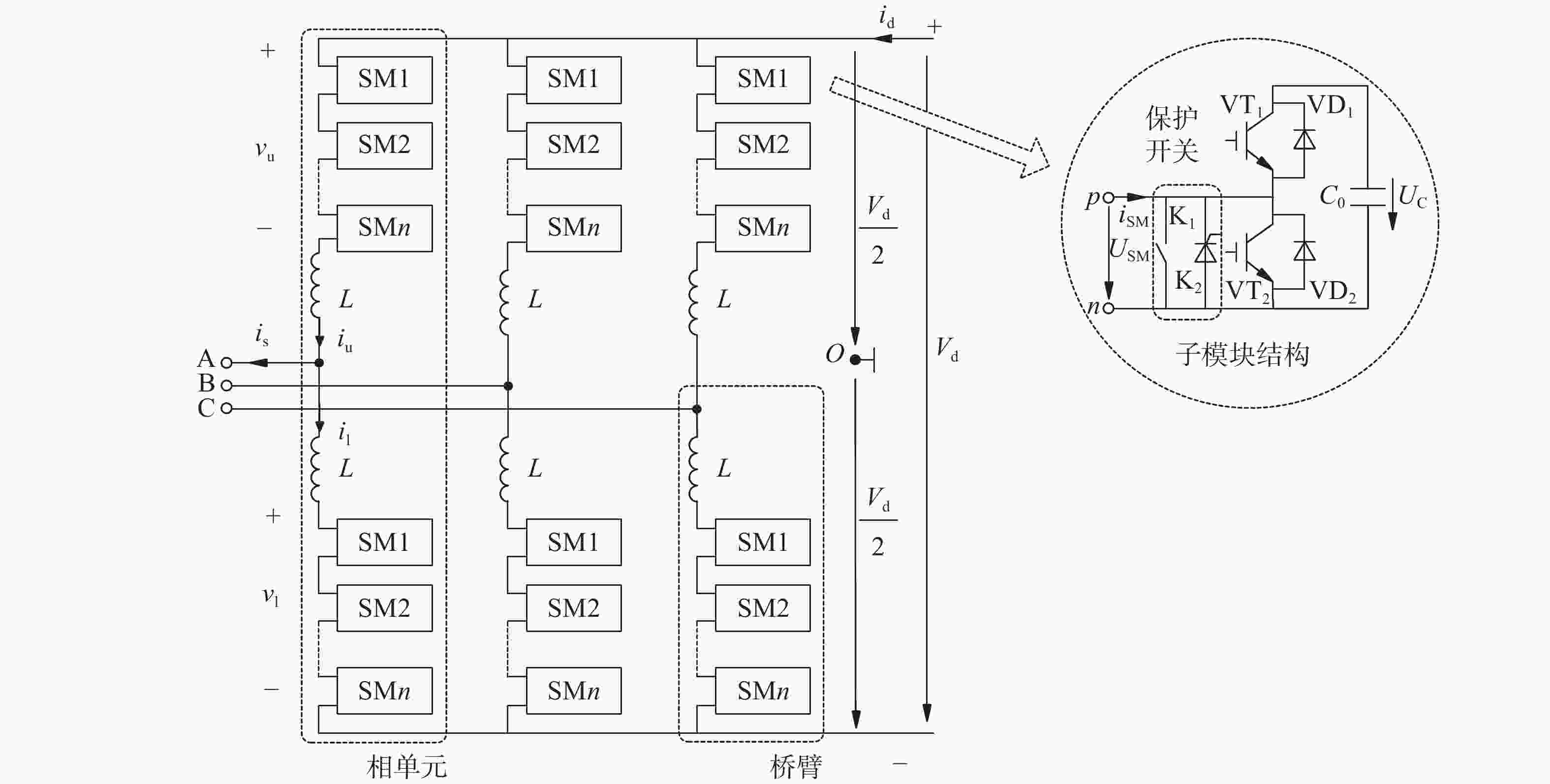
典型的半桥MMC换流器拓扑如图1所示,各相单元含上下两个桥臂,各桥臂单元由N个MMC子模块及桥臂电抗L组成,图中R为子模块等效内阻。子模块采用半桥结构,内含两个具有反并联二极管的IGBT和电容组成,实际工程中每个子模块还含一个保护晶闸管和快速开关。在直流侧通过钳位电容或钳位大电阻接地提供接地钳位点时[25],此时正负极母线上电压分别为Vd/2及−Vd/2。
-
对相单元与交直流侧形成回路的利用基尔霍夫电压定律( Kirchhoff's Voltage Law,KVL)有:
$$ \left\{ {\begin{array}{*{20}{c}} {\dfrac{{{V_{\rm{d}}}}}{2} - {v_{\rm{u}}} - R{i_{\rm{u}}} - L\dfrac{{{\rm{d}}{i_{\rm{u}}}}}{{{\rm{d}}t}} = {v_{\rm{a}}}} \\ { - \dfrac{{{V_{\rm{d}}}}}{2} + {v_{\rm{l}}} + R{i_{\rm{l}}} + L\dfrac{{{\rm{d}}{i_{\rm{l}}}}}{{{\rm{d}}t}} = {v_{\rm{a}}}} \end{array}} \right. $$ (1) 式中:
L ——桥臂电抗值(H);
R ——子模块的等效内阻(Ω);
Vd ——直流电压(kV);
vu、vl ——上、下桥臂端间电压(kV);
iu、il ——上、下桥臂电流(kA),电流方向如图1所示;
va ——阀侧A相相电压(kV)。
对式(1)进行数学变换得:
$$ \left\{ {\begin{array}{*{20}{c}} {\dfrac{L}{2}\dfrac{{{\rm{d}}{i_{\rm{s}}}}}{{{\rm{d}}t}} = \underbrace {\dfrac{{ - {v_{\rm{u}}} + {v_{\rm{l}}}}}{2}}_{{v_{\rm{s}}}} - {v_{\rm{a}}} - \dfrac{R}{2}{i_{\rm{s}}}} \\ {L\dfrac{{{\rm{d}}{i_{\rm{c}}}}}{{{\rm{d}}t}} = - \underbrace {\dfrac{{{v_{\rm{u}}} + {v_{\rm{l}}}}}{2}}_{{v_{\rm{c}}}} + \dfrac{{{V_{\rm{d}}}}}{2} - R{i_{\rm{c}}}} \end{array}} \right. $$ (2) 式中:
is ——阀侧相电流(kA);
ic ——流过桥臂的直流电流分量(kA);
vs ——上下桥臂的差模电压(kV);
vc ——上下桥臂的共模电压(kV)。
式(2)中用到了如下关系[26]:
$$ \left\{ {\begin{array}{*{20}{l}} {{i_{\rm{u}}} = \dfrac{{{i_{\rm{s}}}}}{2} + {i_{\rm{c}}}} \\ {{i_{\rm{l}}} = - \dfrac{{{i_{\rm{s}}}}}{2} + {i_{\rm{c}}}} \end{array}} \right. $$ (3) 根据每个子模块投入切除状态定义单个子模块j(j=1,2,···,N)投入切除的开关状态数nju,l(为1表示投入,为0表示切除),在单桥臂中所有子模块电压均衡时,可得到单个桥臂总投入子模块等效电压为:
$$ {v_{{\rm{cu,l}}}} = \displaystyle \sum\limits_{j = 1}^N {n_{{\rm{u,l}}}^j} v_{{\rm{cu,l}}}^j = \dfrac{{v_{{\rm{cu,l}}}^\Sigma }}{N}\displaystyle \sum\limits_{j = 1}^N {n_{{\rm{u,l}}}^j} = {n_{{\rm{u,l}}}}v_{{\rm{cu,l}}}^\Sigma $$ (4) 式中:
$v_{{\rm{cu,l}}}^\Sigma$ ——上/下桥臂所有子模块电压之和(kV);N ——上/下桥臂子模块个数;
${n_{{\rm{u,l}}}}$ ——上/下桥臂的总开关函数,nu为上桥臂的总开关函数,nl为下桥臂的总开关函数。 -
考虑每个子模块电容电压波动后将其叠加得到桥臂上所有MMC子模块两端电压波动,以上桥臂为例,有:
$$ C\dfrac{{{\rm{d}}v_{{\rm{cu}}}^j}}{{{\rm{d}}t}} = n_{{\rm{u}}}^j{i_{{\rm{u}}}} $$ (5) $$ C\underbrace {\displaystyle \sum\limits_{j = 1}^N {\dfrac{{{\rm{d}}v_{{\rm{cu}}}^j}}{{{\rm{d}}t}}} }_{{\rm{d}}v_{{\rm{cu}}}^\Sigma /{\rm{d}}t} = \displaystyle \sum\limits_{j = 1}^N {n_{{\rm{u}}}^j} {i_{{\rm{u}}}} = {i_{{\rm{u}}}}\underbrace {\displaystyle \sum\limits_{j = 1}^N {n_{{\rm{u}}}^j} }_{N{n_{{\rm{u}}}}} $$ (6) 式中:
C ——MMC子模块电容容值(F)。
替换下标u为表示下桥臂的l,公式依然成立。将式(6)重写得到上下桥臂的总子模块电容电压波动方程如下:
$$ \left\{ {\begin{array}{*{20}{c}} {\dfrac{C}{N}\dfrac{{{\rm{d}}v_{{\rm{cu}}}^\Sigma }}{{{\rm{d}}t}} = {n_{\rm{u}}}(\dfrac{{{i_{\rm{s}}}}}{2} + {i_{\rm{c}}})} \\ {\dfrac{C}{N}\dfrac{{{\rm{d}}v_{{\rm{cl}}}^\Sigma }}{{{\rm{d}}t}} = {n_{\rm{l}}}( - \dfrac{{{i_{\rm{s}}}}}{2} + {i_{\rm{c}}})} \end{array}} \right. $$ (7) 将式(4)代入到vs、vc的公式中,可得到桥臂的总开关函数为:
$$ {n_{\rm{u}}} = \dfrac{{{v_{\rm{c}}} - {v_{\rm{s}}}}}{{v_{{\rm{cu}}}^\Sigma }} {n_{\rm{l}}} = \dfrac{{{v_{\rm{c}}} + {v_{\rm{s}}}}}{{v_{{\rm{cl}}}^\Sigma }} $$ (8) 结合式(7)和式(8),可以得到上下桥臂电容能量的波动方程:
$$ \left\{ {\begin{array}{*{20}{c}} {v_{{\rm{cu}}}^\Sigma \dfrac{C}{N}\dfrac{{{\rm{d}}v_{{\rm{cu}}}^\Sigma }}{{{\rm{d}}t}} = \underbrace {\dfrac{C}{{2N}}\dfrac{{{\rm{d}}{{(v_{{\rm{cu}}}^\Sigma )}^2}}}{{{\rm{d}}t}}}_{{\rm{d}}{W_{\rm{u}}}/{\rm{d}}t} = ({v_{\rm{c}}} - {v_{\rm{s}}})(\dfrac{{i_{\rm{s}}}}{2} + {i_{\rm{c}}})} \\ {v_{{\rm{cl}}}^\Sigma \dfrac{C}{N}\frac{{{\rm{d}}v_{{\rm{cl}}}^\Sigma }}{{{\rm{d}}t}} = \underbrace {\dfrac{C}{{2N}}\dfrac{{{\rm{d}}{{(v_{{\rm{cl}}}^\Sigma )}^2}}}{{{\rm{d}}t}}}_{{\rm{d}}{W_{\rm{l}}}/{\rm{d}}t} = ({v_{\rm{c}}} + {v_{\rm{s}}})( - \dfrac{{i_{\rm{s}}}}{2} + {i_{\rm{c}}})} \end{array}} \right. $$ (9) 从式(9)进一步得到某相单元中上下桥臂总电容能量的波动及上下桥臂电容能量之差的波动方程为:
$$ \left\{ {\begin{array}{*{20}{c}} {{W_\Sigma } = {W_{\rm{u}}} + {W_{\rm{l}}}} \\ {{W_\Delta } = {W_{\rm{u}}} - {W_{\rm{l}}}} \end{array}} \right. \left\{ {\begin{array}{*{20}{c}} {\dfrac{{{\rm{d}}{W_\Sigma }}}{{{\rm{d}}t}} = 2{v_{\rm{c}}}{i_{\rm{c}}} - {v_{\rm{s}}}{i_{\rm{s}}}} \\ {\dfrac{{{\rm{d}}{W_\Delta }}}{{{\rm{d}}t}} = {v_{\rm{c}}}{i_{\rm{s}}} - 2{v_{\rm{s}}}{i_{\rm{c}}}} \end{array}} \right. $$ (10) 表达式中vc=Vd/2;vs=Vscos(w1t);is=Iscos(w1t−φ)。
将上述关系代入式(10)中,可得:
$$ \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{\rm{d}}{W_\Sigma }}}{{{\rm{d}}t}} = {V_{\rm{d}}}{i_{\rm{c}}} - \dfrac{{{V_{\rm{s}}}{I_{\rm{s}}}}}{2}\cos \varphi - \dfrac{{{V_{\rm{s}}}{I_{\rm{s}}}}}{2}\cos (2{w_1}t - \varphi )} \\ {\dfrac{{{\rm{d}}{W_\Delta }}}{{{\rm{d}}t}} = \dfrac{{{V_{\rm{d}}}{I_{\rm{s}}}}}{2}\cos ({w_1}t - \varphi ) - 2{V_{\rm{s}}}{i_{\rm{c}}}\cos ({w_1}t)} \end{array}} \right. $$ (11) 从式(11)的第一个公式可以看出,相单元的总能量变化主要由三部分构成:第一部分为直流分量对应到单相中的有功功率;第二部分为交流系统注入MMC换流器的有功功率;第三部分为表示相间交换的有功,其以二倍频为主,表示相间环流以二倍频为主。
将式(11)两边积分得:
$$ \left\{ {\begin{array}{*{20}{l}} {{W_{_\Sigma }} = {W_{_{\sum 0 }}}\underbrace { - \dfrac{{{V_{\rm{s}}}{I_{\rm{s}}}}}{{4{w_1}}}\sin (2{w_1}t - \varphi )}_{\Delta {W_\Sigma }}} \\ {{W_\Delta } = {W_{\Delta 0}} + \underbrace {\dfrac{{{V_{\rm{d}}}{I_{\rm{s}}}}}{{2{w_1}}}\sin ({w_1}t - \varphi ) - \frac{{2{V_{\rm{s}}}{i_{\rm{c}}}}}{{{w_1}}}\sin ({w_1}t)}_{\Delta {W_\Delta }}} \end{array}} \right. $$ (12) 式中:
$ \Delta {W_\Sigma } $ ——相单元总能量的波动量(MJ);$ \Delta {W_\Delta } $ ——上下桥臂能量差的波动量(MJ)。由于能量储存于子模块电容中,假设不考虑实际工程中的子模块冗余个数,则有:
$$ \left\{ {\begin{array}{*{20}{l}} {{W_{\Sigma 0}} = 2N\times \dfrac{1}{2}C{{(\dfrac{{{V_{\rm{d}}}}}{N})}^2} = \dfrac{{CV_{\rm{d}}^2}}{N}} \\ {{W_{\Delta 0}} = 0} \end{array}} \right. $$ (13) 将式(13)代入式(12)可得到上下桥臂总子模块电容能量为:
$$ \left\{ {\begin{array}{*{20}{c}} {{W_{\rm{u}}} = \dfrac{{{W_\Sigma } + {W_\Delta }}}{2} = \dfrac{{{W_{\Sigma 0}} + \Delta {W_\Sigma } + \Delta {W_\Delta }}}{2}} \\ {{W_{\rm{l}}} = \dfrac{{{W_\Sigma } - {W_\Delta }}}{2} = \dfrac{{{W_{\Sigma 0}} + \Delta {W_\Sigma }-\Delta {W_\Delta }}}{2}} \end{array}} \right. $$ (14) 根据桥臂能量与电容电压之间的关系,结合式(12)~式(14)可最终得到上下桥臂MMC子模块电容电压的详细波动关系如下:
$$ \left\{ \begin{split} &v_{{\rm{cu}}}^\Sigma = \sqrt {\dfrac{{2N}}{C}{W_{\rm{u}}}} = {V_{\rm{d}}}\sqrt {1 + \dfrac{N}{{CV_{\rm{d}}^2}}(\Delta {W_\Sigma } + \Delta {W_\Delta })} \approx \\& {V_{\rm{d}}} + \underbrace {\dfrac{N}{{2C{V_{\rm{d}}}}}(\Delta {W_\Sigma } + \Delta {W_\Delta })}_{\Delta v_{{\rm{cu}}}^\Sigma } \\& v_{{\rm{cl}}}^{_\Sigma } = \sqrt {\dfrac{{2N}}{C}{W_{\rm{l}}}} {\kern 1pt} = {V_{\rm{d}}}\sqrt {1 + \dfrac{N}{{CV_{\rm{d}}^2}}(\Delta {W_\Sigma } - \Delta {W_\Delta })} \approx \\& {V_{\rm{d}}} + \underbrace {\dfrac{N}{{2C{V_{\rm{d}}}}}(\Delta {W_{_\Sigma }} - \Delta {W_\Delta })}_{\Delta v_{{\rm{cl}}}^{_\Sigma }} \end{split} \right. $$ (15) 式中:
$\Delta v_{{\rm{cu}}}^\Sigma$ 、$\Delta v_{{\rm{cl}}}^\Sigma$ ——上、下桥臂子模块电容电压之和的波动量(kV)。为定性初步分析基波分量与二倍频分量的规律,在泰勒展开时忽略了更高频分量,从式(15)可初步得到如下结论:
1)桥臂电容电压和的波动与电容C成反比。
2)上下桥臂的电容电压和的波动均含两部分,一部分为
$ \Delta {W_\Sigma } $ 二倍频分量,一部分为$ \Delta {W_\Delta } $ 基频分量。3)二倍频分量在上下桥臂总大小相等,方向相同;基波分量在上下桥臂上大小相等,方向相反。
-
将式(15)泰勒展开后取其任一项有:
$$ \left\{ \begin{array}{l} {(\Delta {W_\Sigma }{\rm{ + }}\Delta {W_\Delta })^n} = \displaystyle \sum\limits_{k = 0}^n {C_n^k \cdot \Delta {W_\Sigma }^k \cdot \Delta {W_\Delta }^{n - k}} \\ {(\Delta {W_\Sigma } - \Delta {W_\Delta })^n} = \displaystyle \sum\limits_{k = 0}^n {C_n^k \cdot \Delta {W_\Sigma }^k \cdot {{( - \Delta {W_\Delta })}^{n - k}}} \end{array} \right. $$ (16) 对典型项
${C}_{n}^{k}\cdot \Delta {{W}_{\Sigma }}^{k}\cdot\Delta {{W}_{\Delta }}^{n-k}$ 及${C}_{n}^{k}\cdot\Delta {{W}_{\Sigma }}^{k}\cdot {(-\Delta {W}_{\Delta })}^{n-k}$ 进行分析,由于$ \Delta {W_\Sigma } $ 为二倍频分量,$ \Delta {W_\Delta } $ 为基波分量,可以看出$ \Delta {W_\Sigma }^k $ 项仍为偶数倍频,谐波电压的奇偶关系与$ \Delta {W_\Delta }^{n - k} $ 或$ {( - \Delta {W_\Delta })^{n - k}} $ 中n−k的奇偶性相同。因此,可以得到上下桥臂的电容电压波动量的奇数次谐波呈谐波大小相等,方向相反的关系;偶数次谐波大小相等,方向相同的关系。由于电容电压的波动会带来桥臂上的谐波电流,因此,我们可以得出桥臂电流上谐波电流分布规律:1)上下桥臂的奇数次谐波大小相等,方向相反。
2)上下桥臂的偶数次谐波大小相等,方向相同。
3)相间环流为偶数次环流,且以二倍频为主。
4)第1)条等同于MMC阀侧出口交流电压电流只含奇数次谐波。
5)第2)条等同于MMC直流侧电压电流只含偶数次谐波。
6)根据
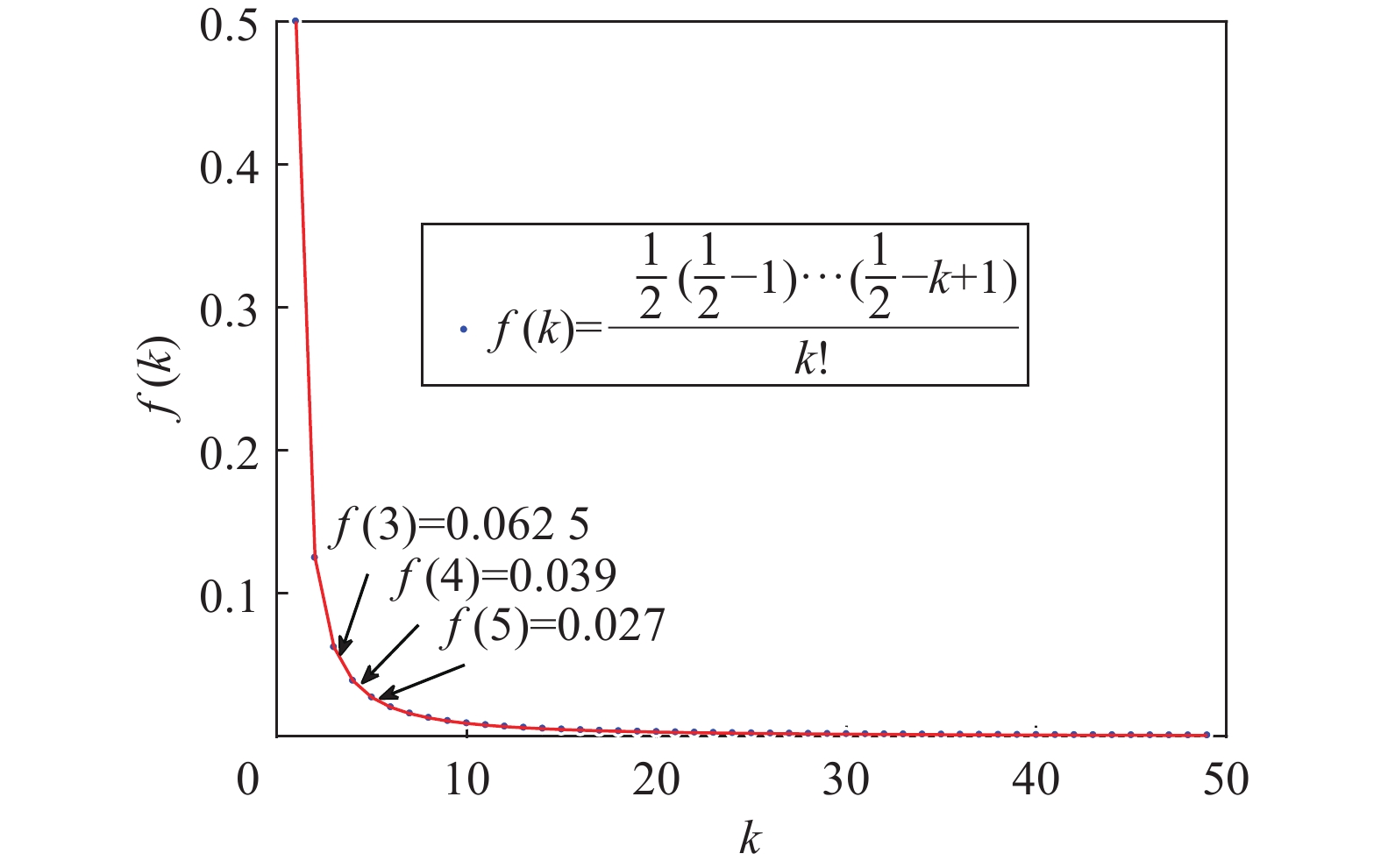
$\Delta {W_\Sigma }$ 和$ \Delta {W_\Delta } $ 的计算公式,可以得到相间环流只含偶数次谐波,其中6k+2次环流呈负序;6k+4次环流呈正序;6k次环流呈零序[12]。从式(17)、式(18)的电容电压波动泰勒展开式出发,考虑取2w1t的相关部分后可以达到二次谐波电流的估算大小。由于高频分量在进行三角函数计算时也有可能产生二倍频分量,这里忽略这些高频分量因中间计算过程带来的二倍频分量的大小,忽略的原因在于随着展开的幂次数的增加,其分量的幅值越来越小,图2给出了泰勒展开式的系数函数随展开阶数的关系。
$$ \begin{split} &v_{{\rm{cu}}}^\Sigma = {v_{\rm{d}}}\sqrt {1 + \dfrac{N}{{Cv_{\rm{d}}^2}}(\Delta {W_\Sigma } + \Delta {W_\Delta })} = {v_{\rm{d}}} + \dfrac{N}{{2C{v_{\rm{d}}}}}(\Delta {W_\Sigma } + \Delta {W_\Delta }) + \cdots + \dfrac{{\dfrac{1}{2} \times \left( {\dfrac{1}{2} - 1} \right) \times \left( {\dfrac{1}{2} - 2} \right) \times \left( {\dfrac{1}{2} - k + 1} \right){v_{\rm{d}}}}}{{k!}} \times \\& {\left[ {\dfrac{N}{{Cv_{\rm{d}}^2}}(\Delta {W_\Sigma }{\text{ + }}\Delta {W_\Delta })} \right]^k} + \cdots \end{split} $$ (17) $$ \begin{split} & v_{{\rm{cl}}}^{_\Sigma } = {v_{\rm{d}}}\sqrt {1 + \dfrac{N}{{Cv_{\rm{d}}^2}}(\Delta {W_\Sigma } - \Delta {W_\Delta })} = {v_{\rm{d}}} + \dfrac{N}{{2C{v_{\rm{d}}}}}(\Delta {W_\Sigma } - \Delta {W_\Delta }) + \cdots + \dfrac{{\dfrac{1}{2} \times \left( {\dfrac{1}{2} - 1} \right) \times \left( {\dfrac{1}{2} - 2} \right) \times \cdots \times\left( {\dfrac{1}{2} - k + 1} \right)}}{{k!}} \times \\& {v_{\rm{d}}}{\left[ {\dfrac{N}{{Cv_{\rm{d}}^2}}(\Delta {W_\Sigma } - \Delta {W_\Delta })} \right]^k} + \cdots \end{split} $$ (18) 得到二次谐波电流的估算大小为:
$$ \begin{split} &{i_\text{2harm}} = \dfrac{C}{N}\frac{{{\rm{d}}\Delta {v_{{\rm{cu}}}}}}{{{\rm{d}}t}} = A\sin (2{w_1}t) + B\cos (2{w_1}t) = \\& \sqrt {{A^2} + {B^2}} \cos(2{w_1}t + \varphi ') \end{split} $$ (19) $$ \begin{split} & A = - \dfrac{{{V_{\rm{s}}}{I_{\rm{s}}}}}{{4{V_{\rm{d}}}}}\sin \varphi - \dfrac{{NV_{\rm{s}}^2i_{\rm{c}}^2}}{{2{w_1}CV_{\rm{d}}^3}} - \dfrac{{NV_{\rm{d}}^2I_{\rm{s}}^2}}{{32{w_1}CV_{\rm{d}}^3}}\cos (2\varphi ) + \\& \dfrac{{N{V_{\rm{d}}}{i_{\rm{c}}}{V_{\rm{s}}}{I_{\rm{s}}}}}{{8{w_1}CV_{\rm{d}}^3}}\cos \varphi \end{split} $$ (20) $$ B = \dfrac{{{V_{\rm{s}}}{I_{\rm{s}}}}}{{4{V_{\rm{d}}}}}\cos \varphi - \dfrac{{NV_{\rm{d}}^2I_{\rm{s}}^2}}{{32{w_1}CV_{\rm{d}}^3}}\sin (2\varphi ) + \dfrac{{N{V_{\rm{d}}}{i_{\rm{c}}}{V_{\rm{s}}}{I_{\rm{s}}}}}{{8{w_1}CV_{\rm{d}}^3}}\sin \varphi $$ (21) -
式(22)、式(23)给出了上、下桥臂子模块电容电压的波动规律,从式子可以知道在忽略高频谐波的情况下桥臂电容电压和的波动与电容C成反比,在直流电压、直流电流、阀侧相电压相电流幅值一定的情况下,子模块电容电压的波动主要取决于阀侧功率因数角φ和时间t。为深入研究,本章节以我国首个海风柔性直流江苏如东工程参数为算列开展,其主参数如表1所示。
参数名 值 额定直流电压/kV ±400 额定直流电流/kA 1.375 额定有功/GW 1.100 额定视在功率/MVA 1230 子模块个数不考虑冗余/个 400 子模块电容容值/mF 4, 6, 8, 9, 10, 12 桥臂电抗器/H 0.133 阀侧相电压峰值/kV 340 阀侧相电流峰值/kA 2.411 Table 1. Parameters for MMC
$$ v_{{\rm{cu}}}^\Sigma = {v_{\rm{d}}}\sqrt {1 + \dfrac{N}{{Cv_{\rm{d}}^2}}(\Delta {W_\Sigma } + \Delta {W_\Delta })} = {v_{\rm{d}}}\sqrt {1 + \dfrac{N}{{Cv_{\rm{d}}^2}}\left( { - \dfrac{{{V_{\rm{s}}}{I_{\rm{s}}}}}{{4{w_1}}}\sin(2{w_1}t - \varphi ) + \dfrac{{{v_{\rm{d}}}{I_{\rm{s}}}}}{{2{w_1}}}\sin({w_1}t - \varphi ) - \dfrac{{2{V_{\rm{s}}}{i_{\rm{c}}}}}{{{w_1}}}\sin({w_1}t)} \right)} $$ (22) $$ v_{{\rm{cl}}}^{_\Sigma } = {v_{\rm{d}}}\sqrt {1 + \dfrac{N}{{Cv_{\rm{d}}^2}}(\Delta {W_\Sigma } - \Delta {W_\Delta })} = {v_{\rm{d}}}\sqrt {1 + \dfrac{N}{{Cv_{\rm{d}}^2}}\left( { - \dfrac{{{V_{\rm{s}}}{I_{\rm{s}}}}}{{4{w_1}}}\sin(2{w_1}t - \varphi ) - \dfrac{{{v_{\rm{d}}}{I_{\rm{s}}}}}{{2{w_1}}}\sin({w_1}t - \varphi ) + \dfrac{{2{V_{\rm{s}}}{i_{\rm{c}}}}}{{{w_1}}}\sin({w_1}t)} \right)} $$ (23) -
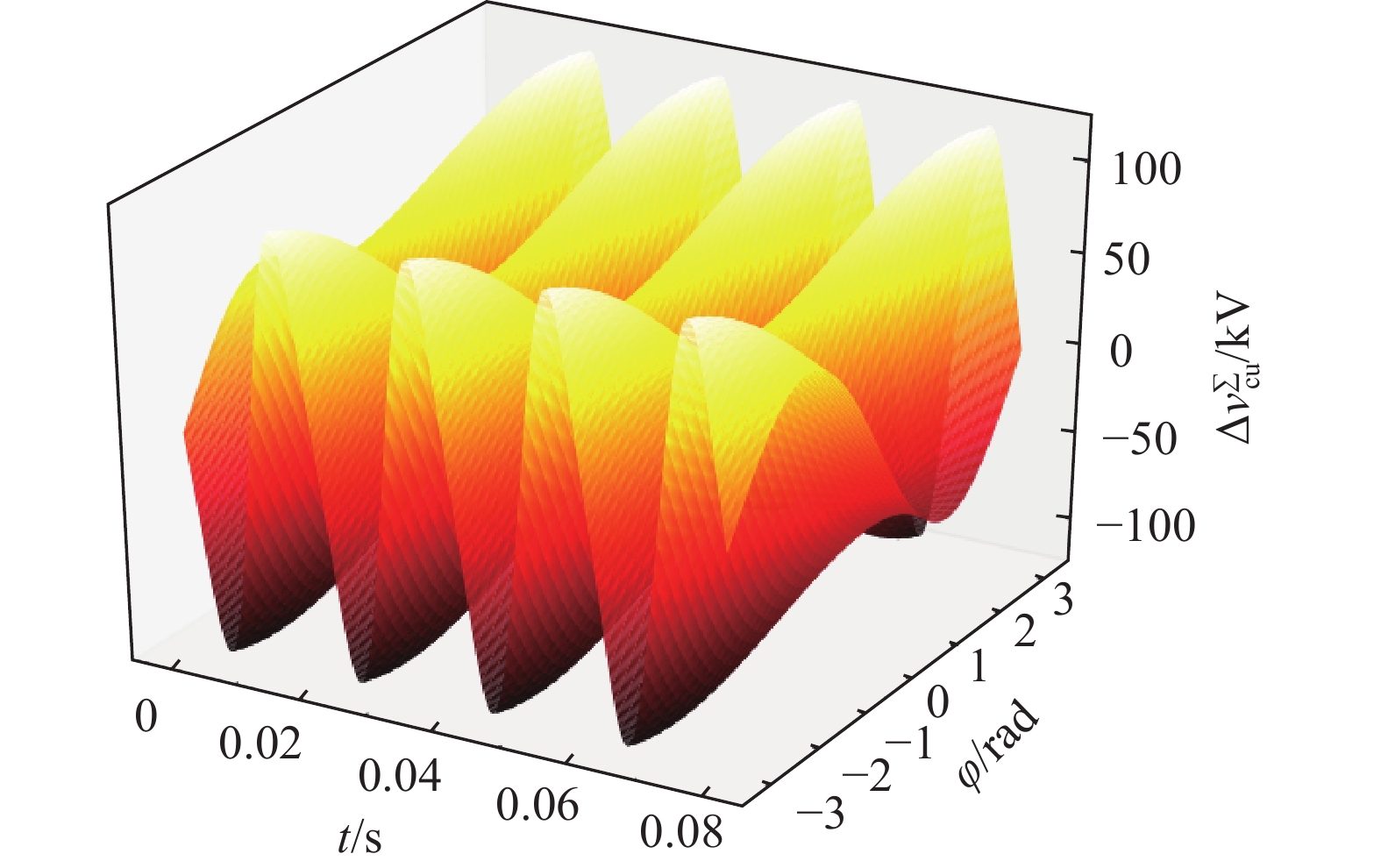
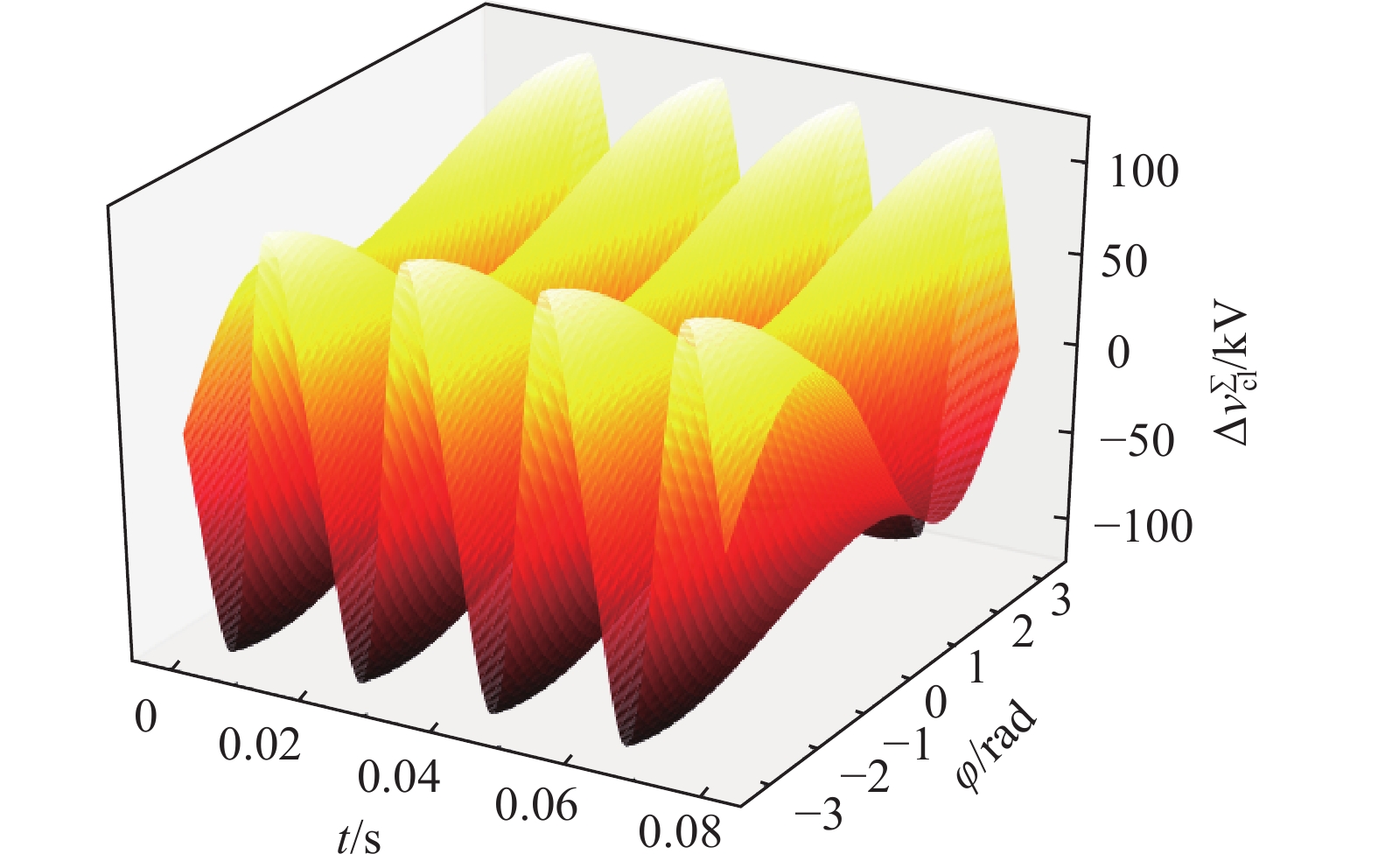
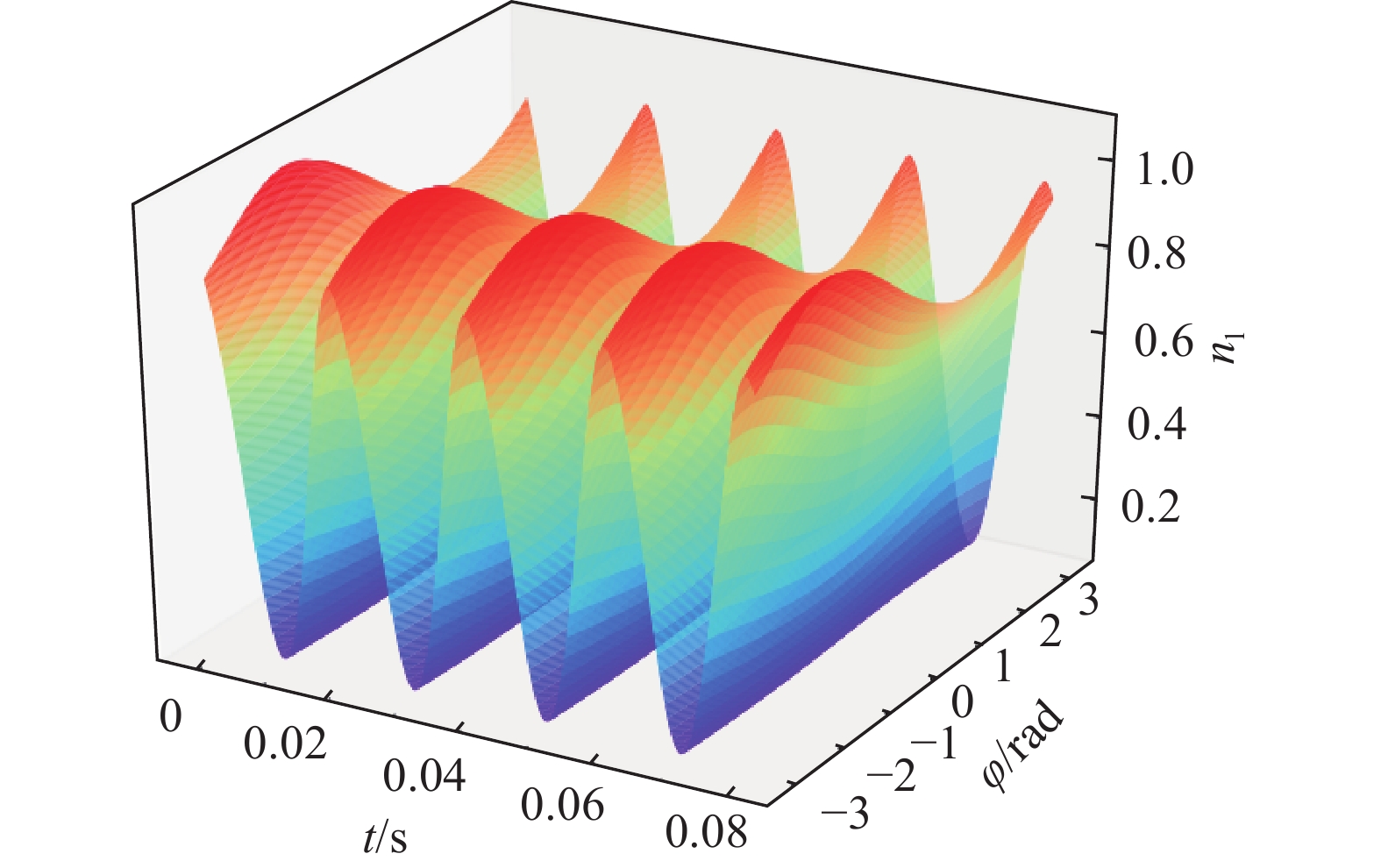
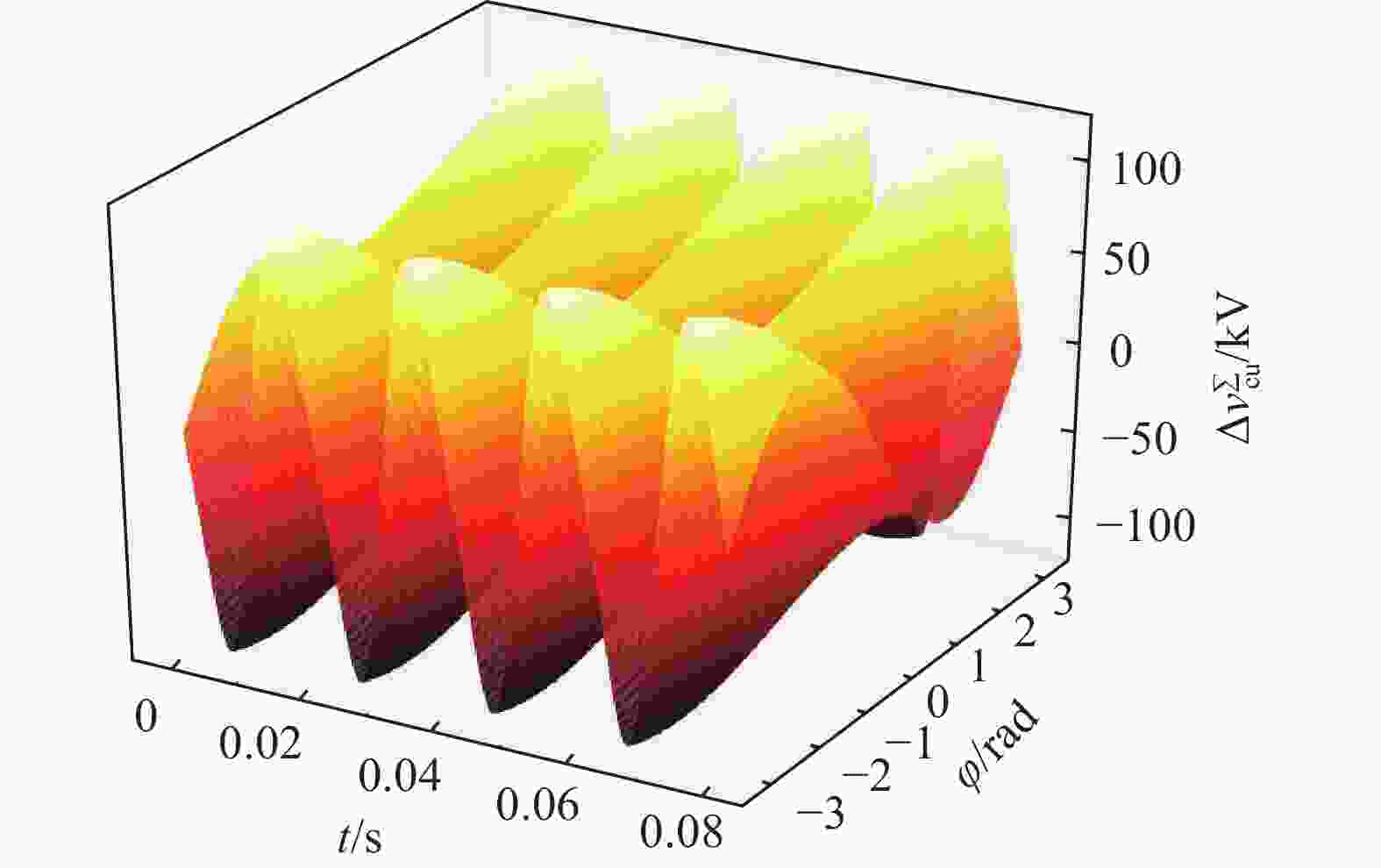
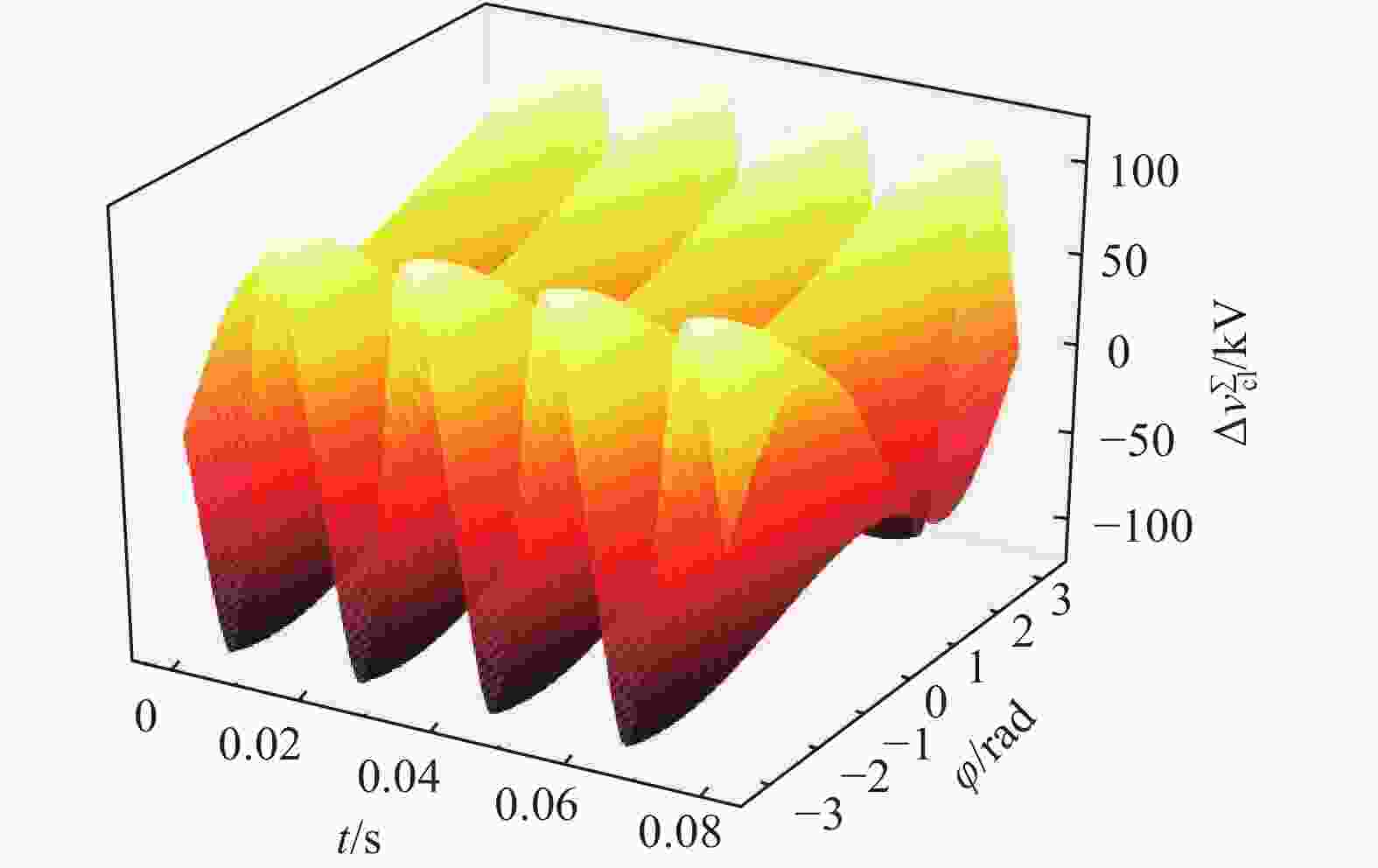
根据式(22)、式(23),假设阀侧电压与阀侧电流的相位差在[−π, π]之间变动,考虑4个工频周期下的波动,得到如下三维关系图,其中x轴坐标为时间t(单位为s),y轴坐标为相角差φ(单位为rad),z轴坐标为桥臂子模块电容电压的波动量
$\Delta v_{{\rm{cu}}}^\Sigma$ (单位为kV),根据前面式子,得到上下桥臂所有投入的子模块电容电压的波动随时间及阀侧电压初始相位差的三维关系图,如图3及图4所示。从上图可知,在φ=0时,MMC换流阀与交流侧没有无功交换,此时桥臂子模块电容电压波动的峰值最小。在φ减小或增大的过程中,波动量均在一定程度上增大。
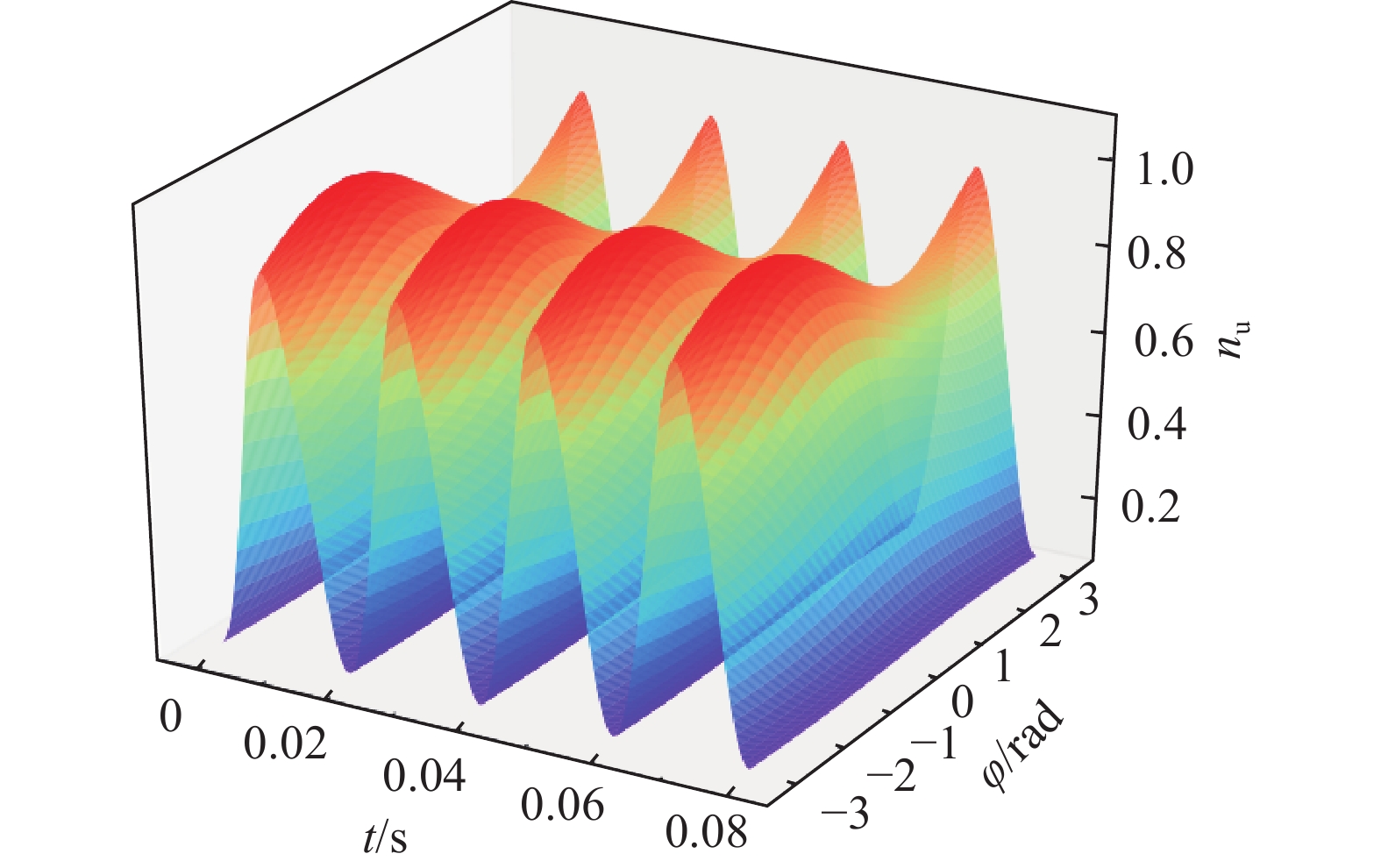
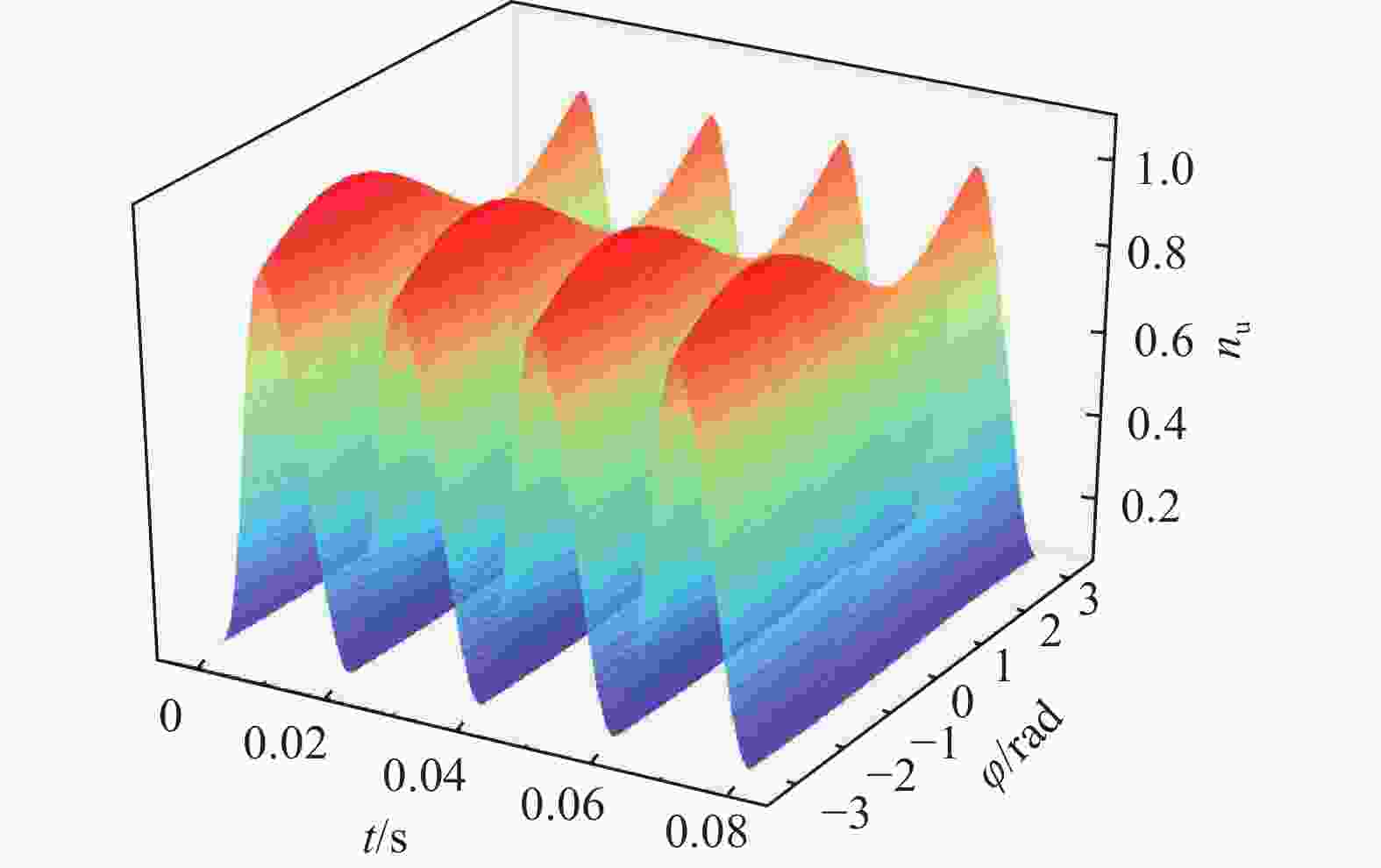
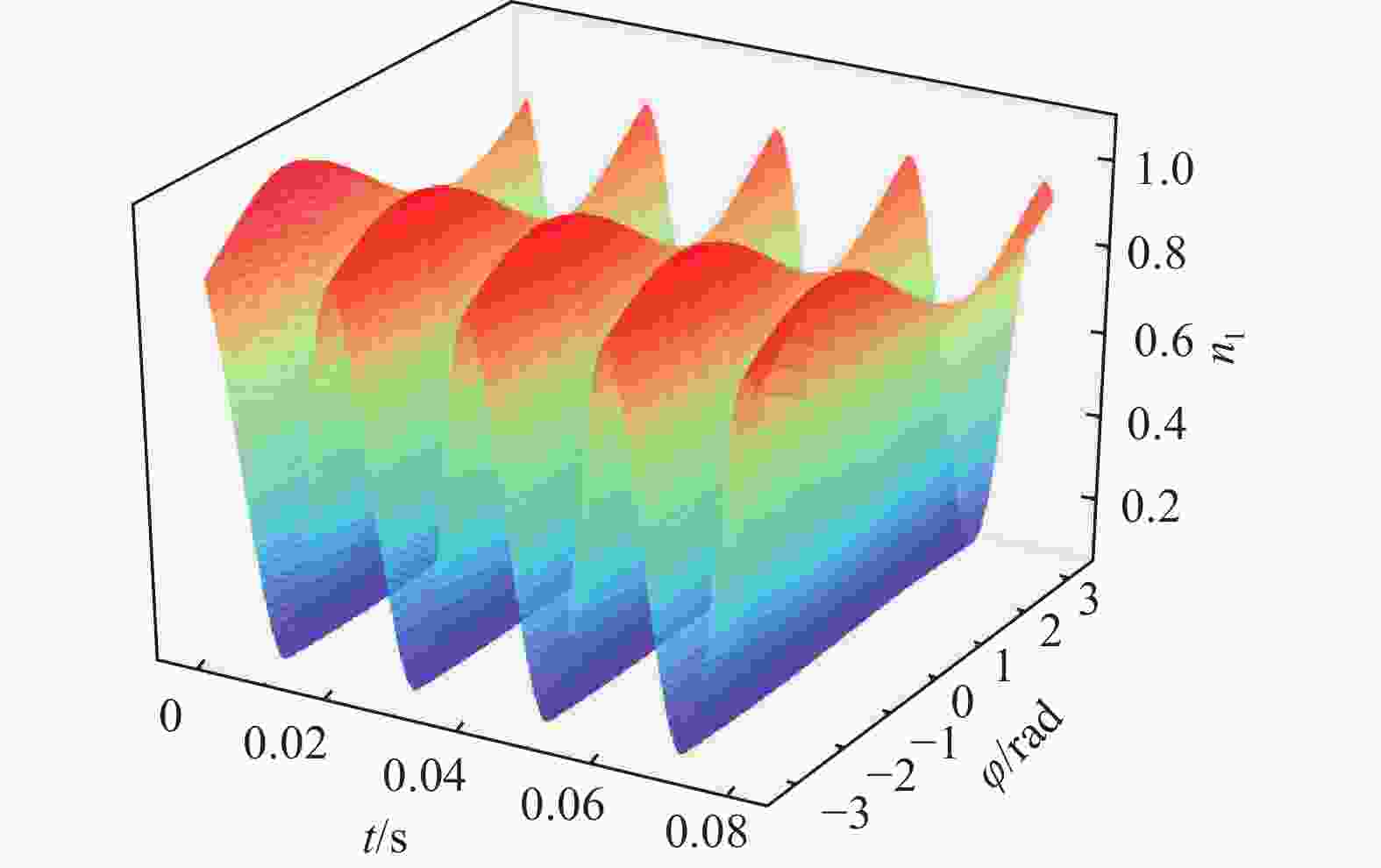
根据式(8)同样可得到上下桥臂的总开关函数nu、nl随时间及功率因数角φ的曲线图。其中x轴坐标为时间t(单位为s),y轴坐标为相角差φ(单位为rad),z轴坐标为桥臂总子模块开关函数,图5为上桥臂总开关函数图,图6为下桥臂总开关函数图。
从图5和图6可以明显看出,功率因数角φ一定时桥臂总开关函数是时间t的三角工频周期函数,在时间t一定时,开关函数是功率因数角的周期函数,且在φ<0的一定范围内,开关函数的最大值大于1,这是由于φ<0时,换流器向交流系统注入容性无功,在[−90°, 0]范围内,φ越小注入容性无功越大,此时同等有功条件下需要投入的子模块个数越多。将式(15)代入式(8)以后,可得到上下桥臂的开关函数的表达式,这里仅列出下桥臂开关函数:
$$ {n_{\rm{l}}} = \dfrac{{{V_{\rm{d}}}/2 + {V_{\rm{s}}}\cos {w_1}t}}{{{V_{\rm{d}}} + \Delta v_{{\rm{cl}}}^\Sigma }} $$ (24) $$ \begin{split} &\Delta v_{{\rm{cl}}}^\Sigma = \dfrac{N}{{2C{v_{\rm{d}}}}}[ - \dfrac{{{V_{\rm{s}}}{I_{\rm{s}}}}}{{4{w_1}}}\sin (2{w_1}t - \varphi ) - \dfrac{{{v_{\rm{d}}}{I_{\rm{s}}}}}{{2{w_1}}}\sin ({w_1}t - \varphi ) + \\& \dfrac{{2{V_{\rm{s}}}{i_{\rm{c}}}}}{{{w_1}}}\sin ({w_1}t)] \end{split} $$ (25) t=0时刻,有桥臂最大的开关函数为:
$$ {n_{\rm{l}}}{|_{\max}} = \dfrac{{{V_{\rm{d}}}/2 + {V_{\rm{s}}}}}{{{V_{\rm{d}}} + \dfrac{{N{I_{\rm{s}}}}}{{4{w_1}C}}(\dfrac{{{V_{\rm{s}}}}}{{2{V_{\rm{d}}}}} + 1)\sin \varphi }} $$ (26) 在开关函数最大值为1的情况下,此时得出:
$$ \mathrm{sin}\varphi =\dfrac{4{w}_{1}C}{N{I}_{{\rm{s}}}}\times \dfrac{{V}_{\rm{s}}-\dfrac{{V}_{\rm{d}}}{2}}{\dfrac{{V}_{{\rm{s}}}}{2{V}_{\rm{d}}}+1} $$ (27) 由于阀侧相电压最大值小于直流电压的一半,可以看出在开关函数的最大值为1时,功率因数角φ∈[−π/2, 0],这与图中结论一致。
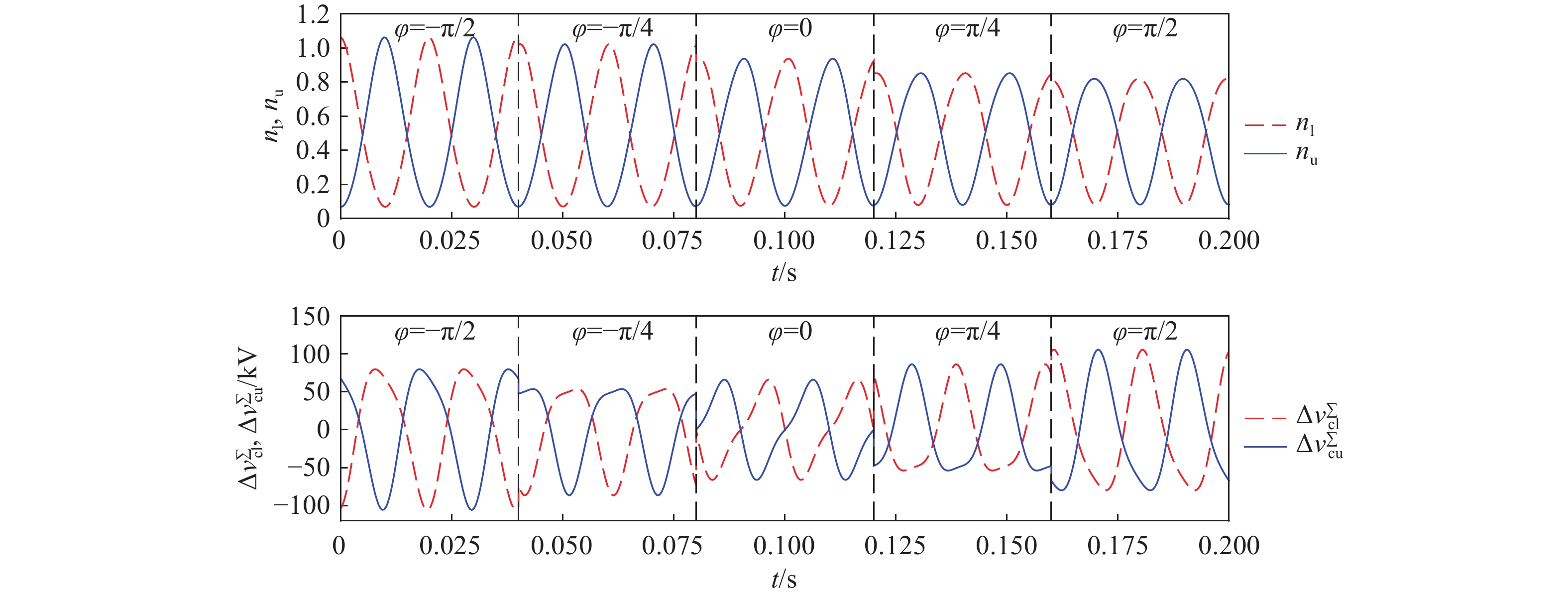
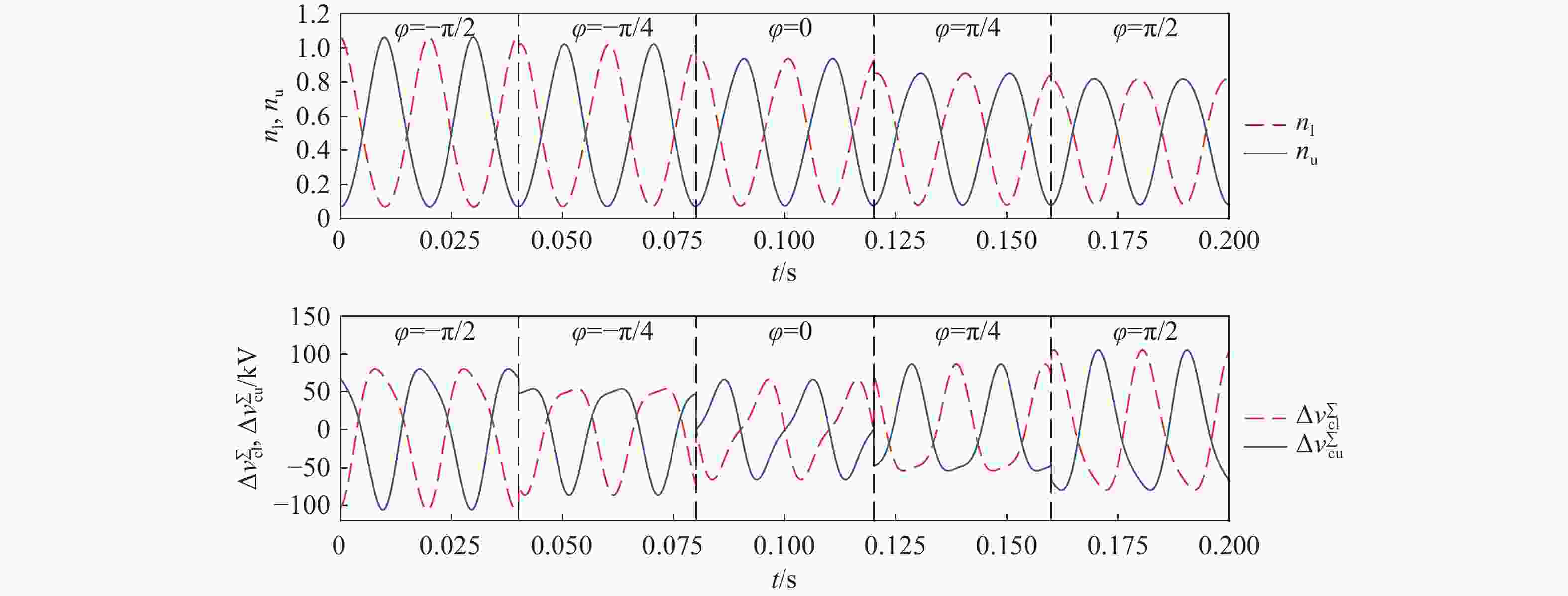
为进一步分析开关函数与模块电容电压随功率因数角的变换关系,给出了不同功率因数角下的开关函数及桥臂子模块电容电压波动的关系图(图7)。从图中及式(24)可得到如下结论:
1)桥臂开关函数的最大值在φ∈[−π/2, π/2]范围内单调递减,且在[−π/2, 0]内某点φ0处其最大值为1。
2)在额定视在功率一定的情况下,桥臂开关函数的最大值在φ<0的某些范围内会呈现大于1的情况,此时功率因数较小,理论交换无功较大,φ=−90°时换流器工作在STATCOM工况下,实际工程中采用限幅环节对开关函数进行限幅。
3)子模块电容电压纹波存在明显的二倍频和基波分量。
4)在低功率因数φ=±90°下,子模块电容电压纹波比高功率因数下的纹波更大,且在低功率因数下子模块电容电压波动呈现正负半周期不对称现象。
-
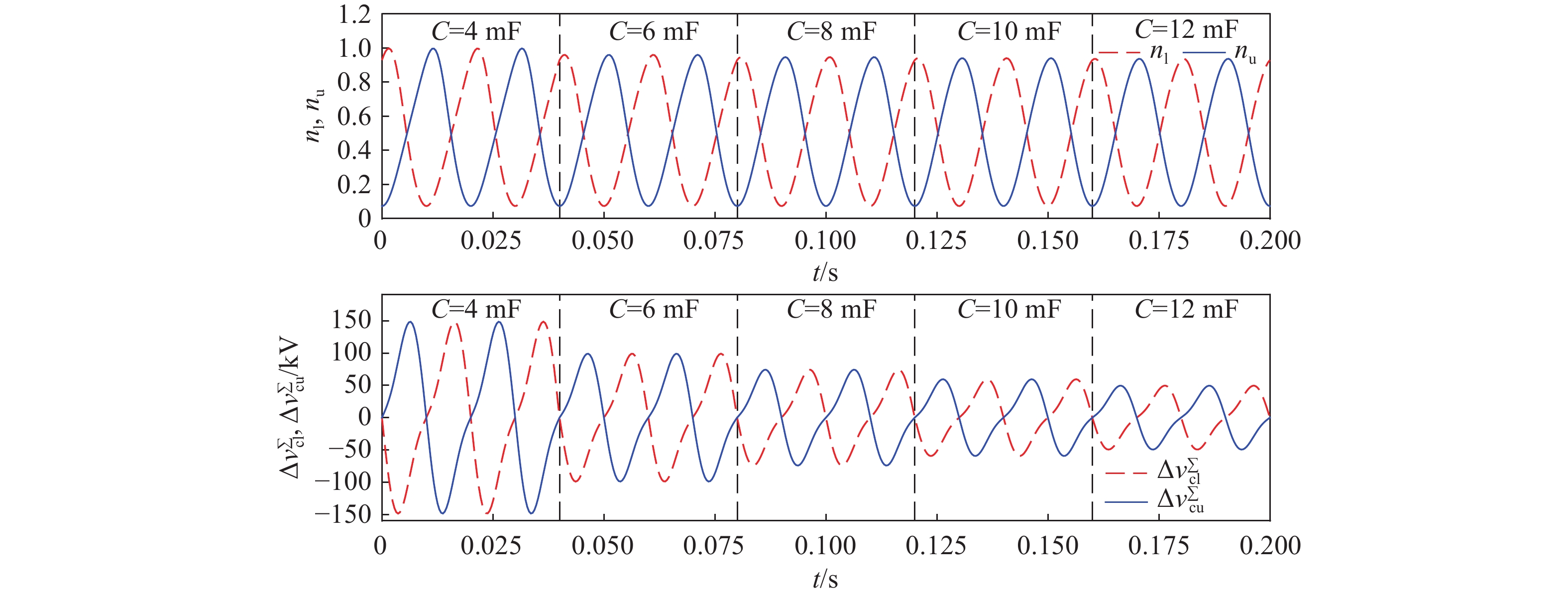
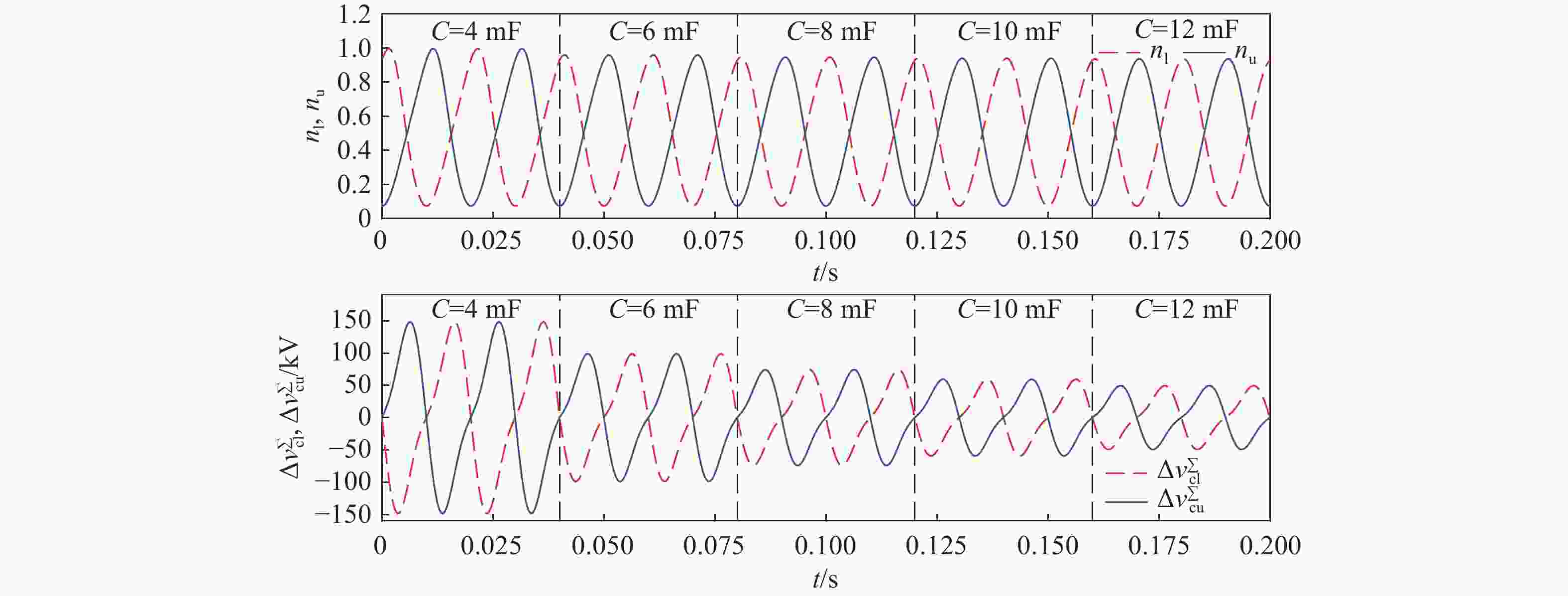
考虑φ=0时,子模块电容电压及桥臂开关函数随电容容值的变化关系。图8给出了表1参数下的桥臂开关函数及电容电压波动随时间和电容容值的变化。
从图8中可知,在φ=0时,桥臂开关函数的最大值不随电容电压的变化而变化,进一步从式(20)中可知,在φ≠0时,开关函数的最大值一定程度上随电容容值的变大而变小。子模块电容电压的波动量随着电容容值的变大而减少。
-
为验证上述结论,在PSCAD/EMTDC仿真软件中搭建了上述表1参数下的仿真模型。
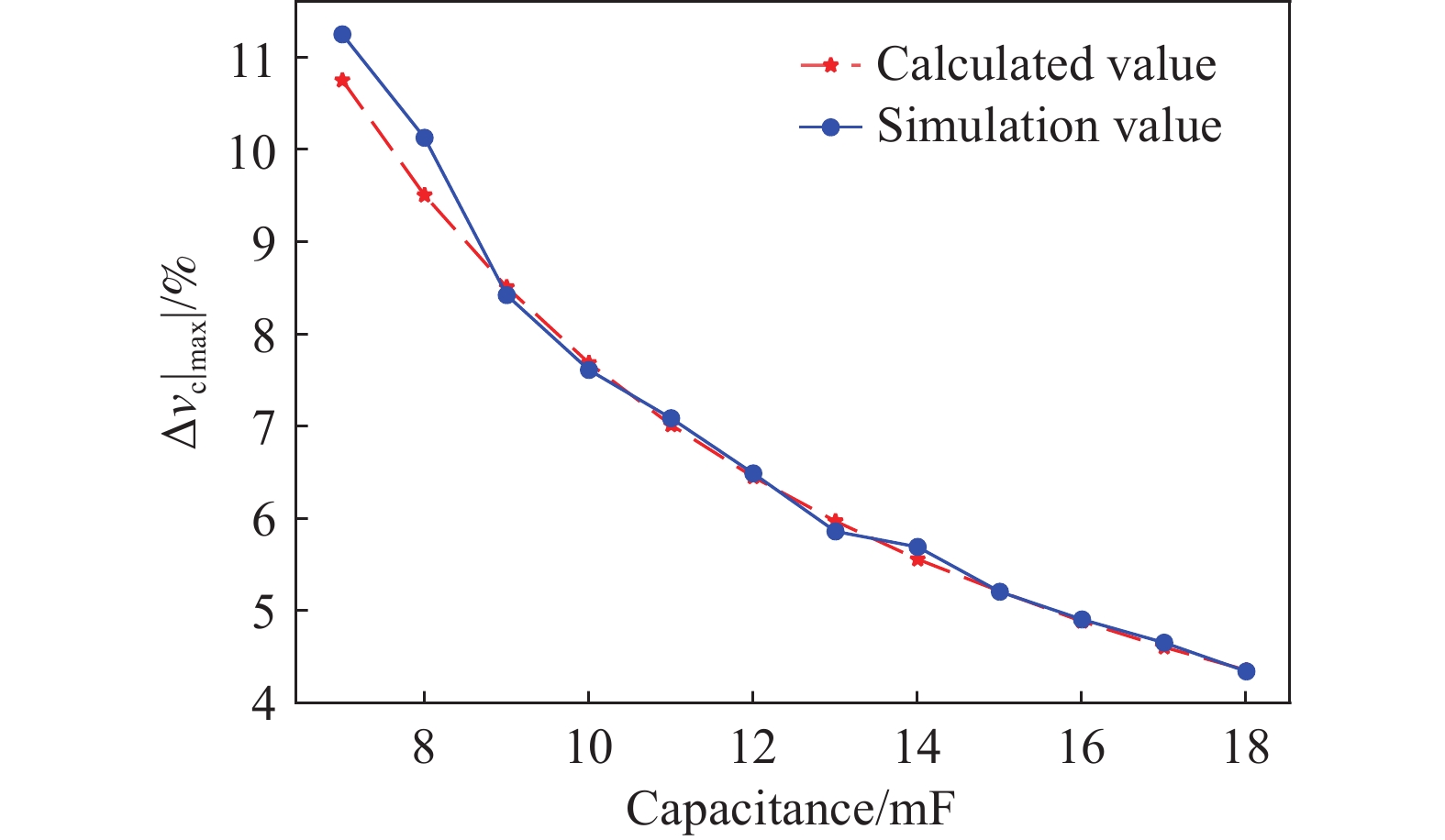
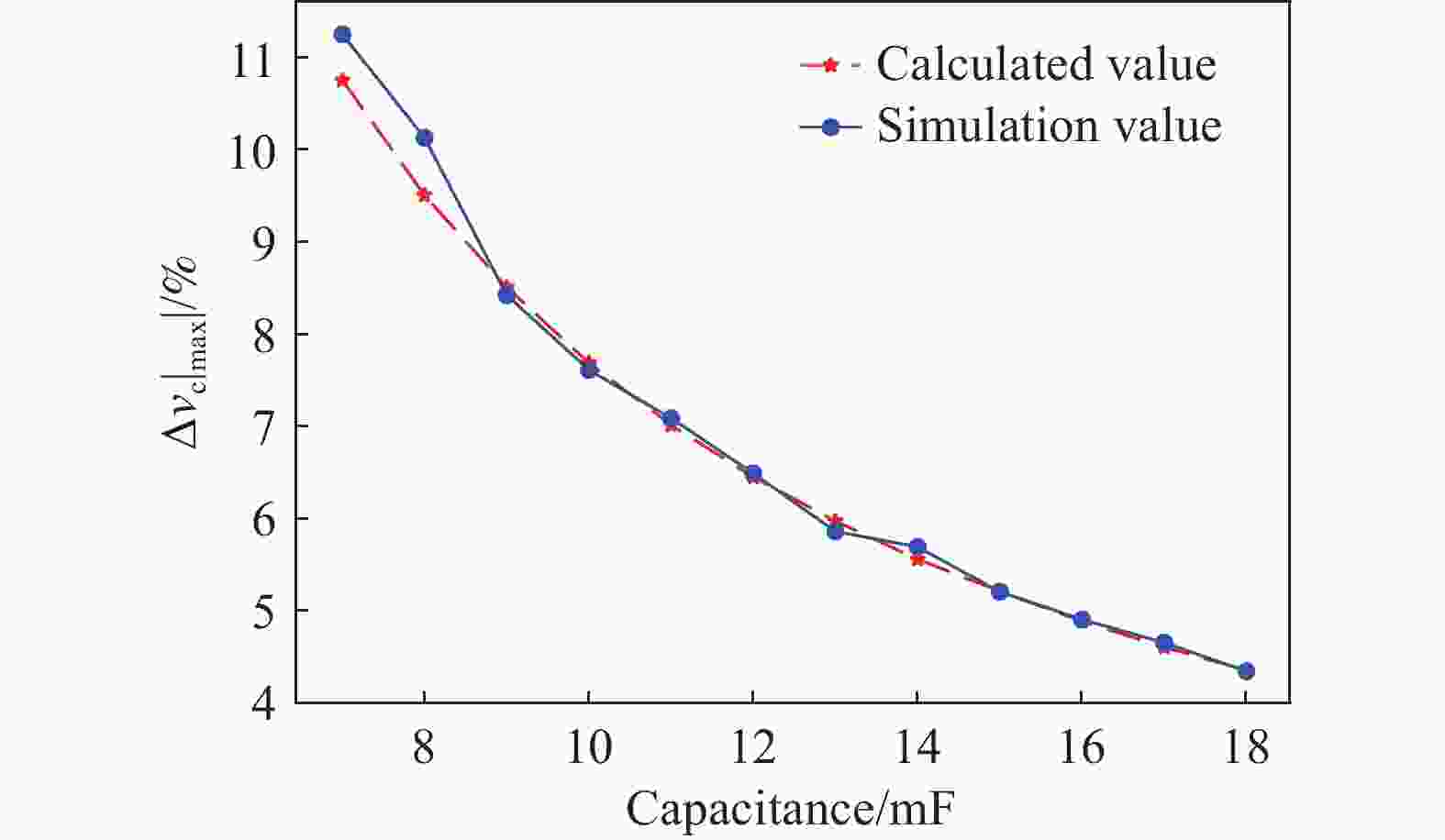
为验证子模块电容电压波动随子模块电容容值的变化,图9给出了计算与仿真的对比关系图,其横坐标为子模块电容容值,纵坐标为电容电压的波动幅值相对基准值的占比,可看出子模块电容电压波动幅值随容值的变大而减小,理论计算值与仿真值较为吻合。
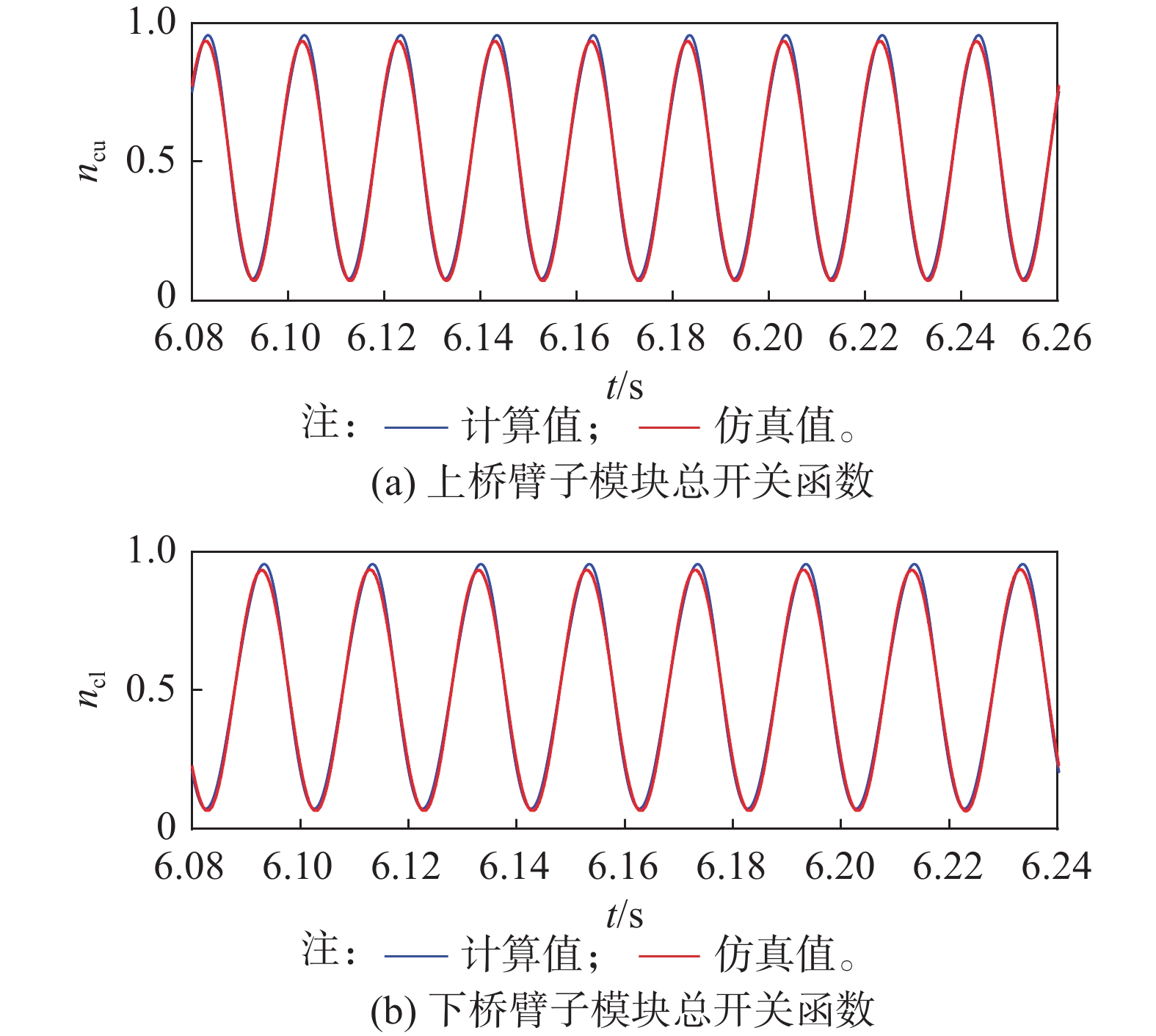
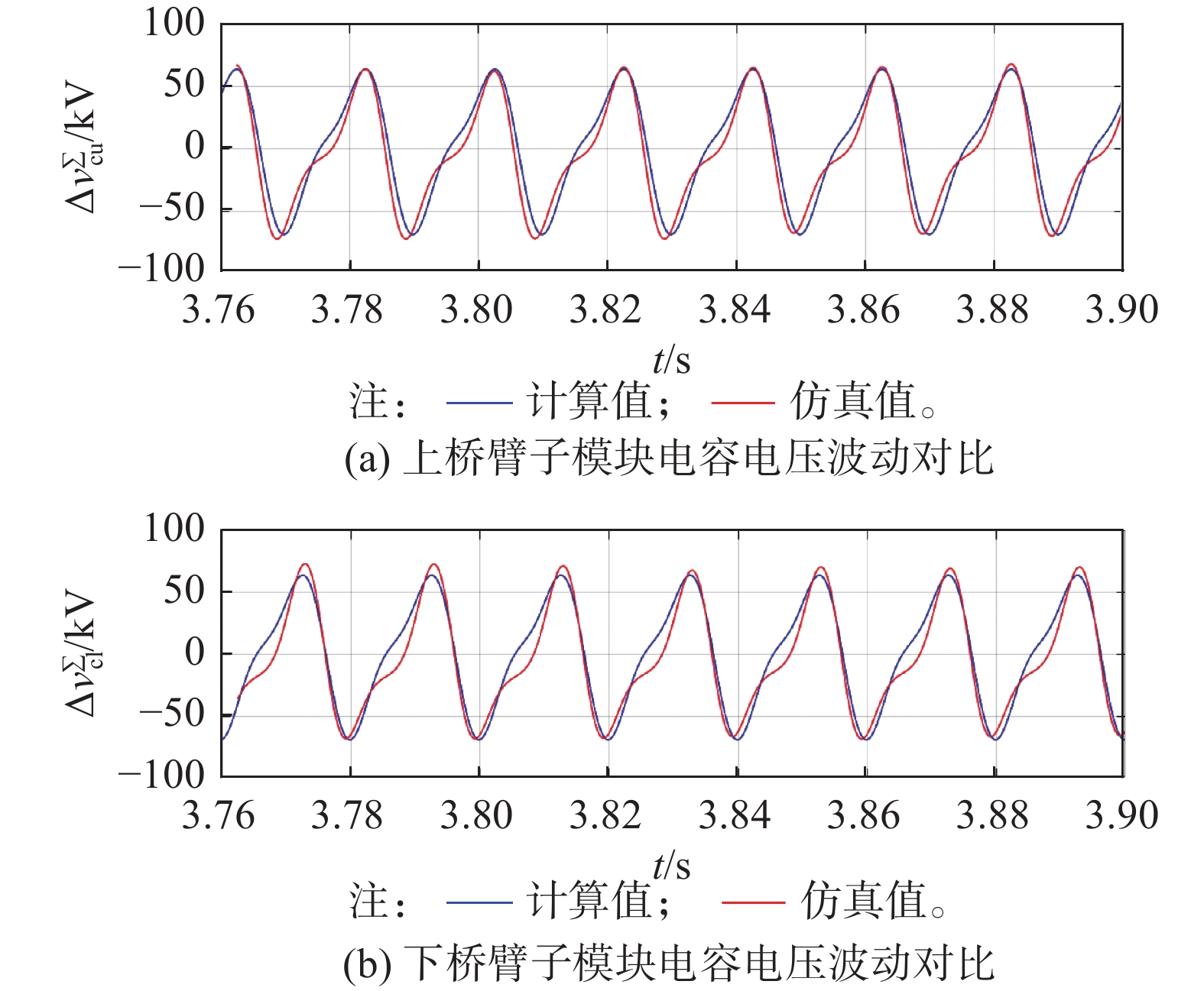
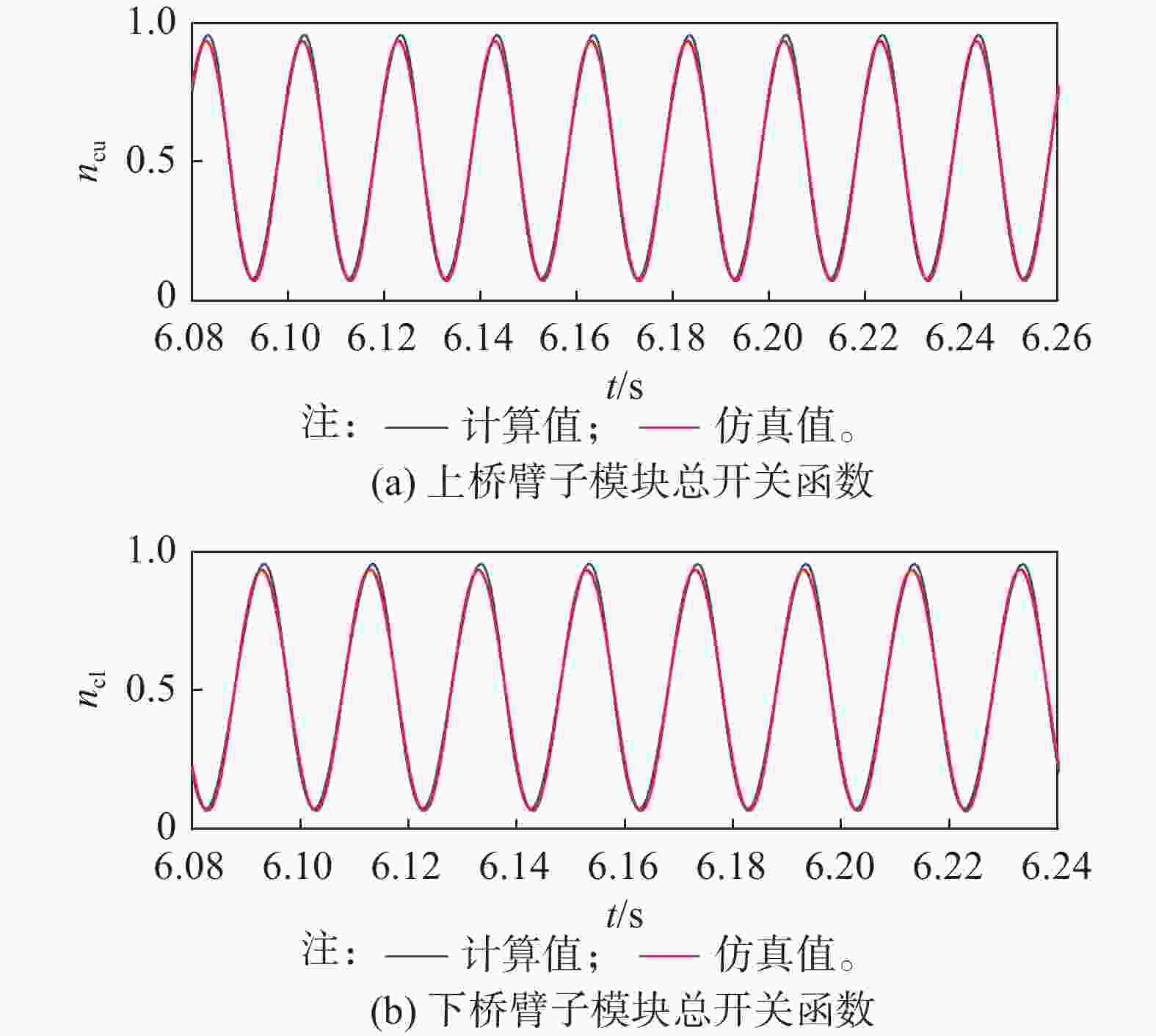
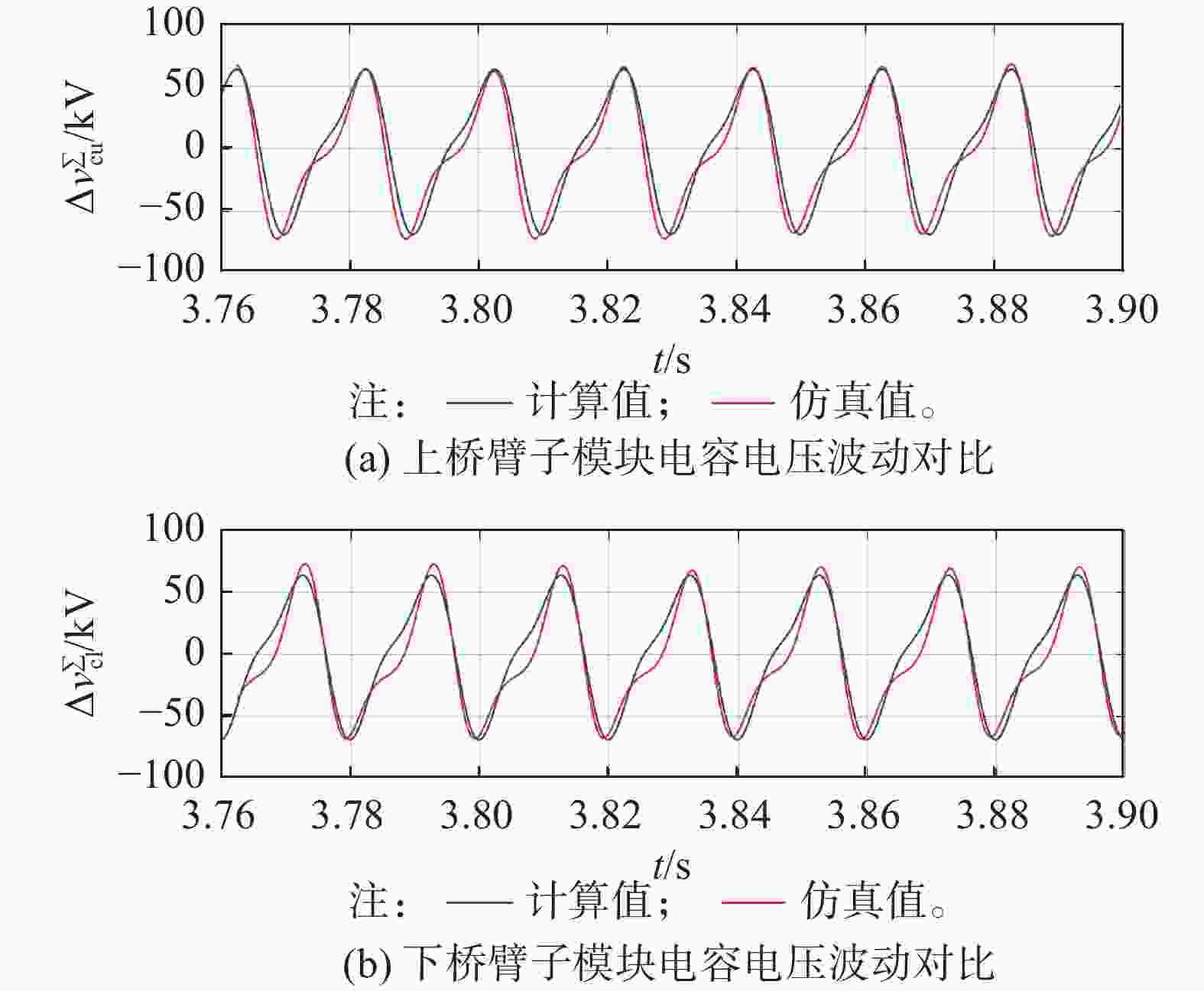
为验证子模块电容电压波动实时曲线及桥臂开关函数的实时曲线,在仿真模型中任取一个PQ功率点(1100 MW, 123 Mvar)下对两者进行了对比。从图10对比中可看出在任取的功率点下,上下桥臂开关函数理论计算值与仿真值吻合度较高。图11给出了上下桥臂子模块电容电压实时波动的对比,可看出计算与仿真总体较为吻合,在模块电容电压波动过零点处的不一致主要是由于计算中未考虑二次以上的高倍频谐波波动导致。
-
文章从能量角度出发得到了桥臂电容电压、桥臂开关的理论计算值,在此基础上研究了桥臂谐波的特性,并深入研究了子模块电容电压的波动和桥臂开关函数的情况,主要得出的结论与仿真结果一致,为实际工程中MMC换流器设计提供了参考。
但是,文章对换流器建模尚未结合换流器自身控制系统,后续可开展结合控制系统的换流器阻抗建模研究及换流器自身调制环节、控制链路等MMC稳定性影响因子分析;另一方面,通过注入倍频环流或先进控制方式可降低模块电容电压的波动,以优化系统参数的选型,这也是后续待研究之一。
Capacitor Voltage Ripple and Harmonics Analysis in MMC
doi: 10.16516/j.gedi.issn2095-8676.2023.05.016
- Received Date: 2023-03-20
- Rev Recd Date: 2023-06-26
- Available Online: 2023-09-06
- Publish Date: 2023-09-10
-
Key words:
- MMC /
- capacitor voltage ripple /
- switching function /
- harmonic voltage /
- harmonic current
Abstract:
| Citation: | ZOU Kaikai, LI Gang, ZOU Qiang, DONG Yunlong, LU Yu. Capacitor Voltage Ripple and Harmonics Analysis in MMC[J]. SOUTHERN ENERGY CONSTRUCTION, 2023, 10(5): 129-138. doi: 10.16516/j.gedi.issn2095-8676.2023.05.016 |




















































 DownLoad:
DownLoad: