-
根据电压等级,配电台区可分为高压配电台区、中压配电台区和低压配电台区。文章研究的低压配电台区是指10 kV/400 V公共配电变压器下的居民区。低压配电台区网络主要是一个径向网络,从配电变压器的低压侧出口开始,到每个用户的接入点结束。供电部门记录的正确的拓扑信息有助于工作人员监测电网信息,分析故障,优化电网运行,满足低压配电台区精益化、智能化管理的需要[1]。
目前,各式新型用电设备及用户的加入使低压配电网络结构呈现出持续变化的特征。因此,开展低压台区拓扑关系识别研究具有重要的工程应用价值。
低压台区配电网拓扑识别类型可归纳为以下4种:(1)识别低压台区与10 kV馈线的从属关系,该层关系识别错误率较低;(2)识别低压用户与低压台区的从属关系,部分用户易被误识别到邻近台区;(3)识别低压用户与电表表箱的从属关系,部分用户易被误识别到邻近表箱;(4)识别低压用户的相位信息。
目前,主流的拓扑结构识别方法可分为人工检测法、信号标记法和数据分析法[2-3]。传统的人工检测法和信号标记法需要投入大量的人力成本和设备维护成本,经济效益低[4-6]。数据分析方法是基于先进的计量基础设施所收集的大量电气测量数据,如电压和电流[7],通过分析每个电气量的空间和时间特征,得出每个节点的潜在连接关系。因此,与人工检测法和信号标记法相比,数据分析法更加高效、便捷和环保,是目前低压配电网络拓扑识别问题的一个重要研究方向。因此,国内外大量专家学者都相继在拓扑识别领域展开了数据分析法的研究。
文献[8]和文献[9]识别配电网10 kV母线之间的连接关系,即不同联络线上隔离开关闭合或断开时所形成的不同拓扑结构。文献[10]提出了识别电能表与低压配电网一级分支线(即低压配电网首端出线)的归属关系的方法。基于T型灰色关联度和K-最近邻算法,结合供电部门记录的原拓扑结构图,文献[11]提出了识别低压台区和10 kV的从属关系以及识别低压用户与台区的从属关系的方法。文献[12]通过对智能电表采集的电气量数据的读取分析,提出了基于主成分分析及其图论解释来生成稳定状态的网络拓扑。文献[13]使用智能电表数据,根据每小时电压曲线的相关因素和相对幅度水平,检测变压器附近错误连接的用户。文献[14]和文献[15]利用高质量电表电量数据,分别基于分层聚类算法以及半监督约束聚类算法解决单一台区的用户相位信息识别问题。
总体而言,现有的拓扑识别方法大多只能识别低压配电网络的一种拓扑关系,很少有方法能识别一个完整拓扑的两种以上的连接信息[16]。同时,目前方法在应用到大规模低压台区上时,准确率仍然无法达到实际工程上的要求[9]。
在此背景下,针对当前拓扑识别研究中缺少低压用户归属台区误挂问题的识别方案以及多台区混合用户数据下用户相序识别方法的研究,文章提出了基于密度聚类的低压台区归属关系及相位识别方法。文章首先在阐述了对用户电压数据进行预处理的方法;接着详述了文章所用的t分布随机近邻嵌入降维方法(t-distributed Stochastic Neighbor Embedding,t-SNE)与基于数据密度的噪声应用空间聚类方法(Density-Based Spatial Clustering of Applications with Noise,DBSCAN)的算法原理;最后,通过对实际数据进行算法应用分析,验证所提方法的有效性与实用性。
-
文章算法需要用到的有效数据信息主要有用户测量点编号或智能电表编号、采集数据对应的时间信息与采集到的用户电压信息。因此,需要从供电公司的用户用电数据文件中对该类有效数据进行有效提取并生成电压数据矩阵U,如式(1)所示。
$$ {\boldsymbol{U}} {\text{ = }}\left[ {\begin{array}{*{20}{c}} {{U_{1,{{t}_1}}}}&{{U_{1,{{t}_2}}}}& \cdots &{{U_{1,{{t}_q}}}} \\ {{U_{2,{{t}_1}}}}&{{U_{2,{{t}_2}}}}& \cdots &{{U_{2,{{t}_q}}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{U_{{p},{{t}_1}}}}&{{U_{{p},{{t}_2}}}}& \cdots &{{U_{{p},{{t}_q}}}} \end{array}} \right] $$ (1) 式中:
${U_{{j},{{t}_{k}}}}$ ——电表$ j $ 在$ {t_k} $ 时刻测量的电压幅值;$ p $ ——每一台区用户数量或节点数相加的总和;$ q $ ——在一定时间段内的采样点数量,作为每个用户或节点的原始完整特征维度。目前智能电表采集的数据精度还较低,采集的电压数据样本标准不一,给电压数据分析工作造成了不小的困难,甚至会直接影响后期降维聚类的精准度。因此,文章选用Z-Score方法对U进行归一化处理,方法表达式如下:
$$ {{\boldsymbol{U}}'_{{{t}_{j}}}} = \dfrac{{{U_{{{t}_{j}}}} - \mu \left( {{U_{{{t}_{j}}}}} \right)}}{{\sigma \left( {{U_{{{t}_{j}}}}} \right)}}{\text{, }}j = 1,2, \cdots ,n $$ (2) 式中:
${{\boldsymbol{U}}'_{{{t}_{j}}}}$ ——电压经标准化处理后在tj采样时刻下所有台区用户节点电压列向量;${{\boldsymbol{U}}_{{{t}_{j}}}}$ ——在tj采样时刻所有台区用户节点量测电压值列向量;$\mu \left( {{U_{{{t}_{j}}}}} \right)$ ——在tj采样时刻下所有台区用户节点的电压均值;$\sigma \left( {{U_{{{t}_{j}}}}} \right)$ ——在tj采样时刻下所有台区用户节点的电压标准差;n ——表计采集的用户节点电压采样时刻总数。
-
未经处理的高维时序电压数据中包含有异常干扰信息,会在台区辨识与相位辨识过程中引入误差,影响准确率。而降维可以对高维数据内部的本质结构进行有效提取,减少低可信度信息造成的误差,提高辨识精度。同时,数据维度的降低更便于计算机处理和可视化操作,缓解了高维空间数据的维度灾难,有效提高了辨识效率。
-
在数据挖掘领域,目前已经存在着大量成熟的数据降维算法,可以分为线性降维算法与非线性降维算法两大类,主要区别在于降维算法使用的映射函数的不同。主成分分析法(Principal Component Analysis,PCA)作为经典线性降维算法的代表,其基于数据线性变换原理将高维数据线性映射到低维坐标中[17],具有计算简便高效、不受标签限制的优点,但无法通过修改算法输入参数等方法对算法的降维处理过程进行可变性的人为干预,对数据泛化能力差,不适于处理拓扑复杂用户量大的高维时序电压数据;局部线性嵌入方法(Locally Linear Embedding,LLE)作为流形学习的代表,其基于高维数据点与点之间的线性组合重构出保留点与点之间局部关系的低维数据[18],优点是能够学习高维数据的局部线性低维流形,有利于数据点间关系辨识,算法输入参数少,调参简便,缺点是降维数据受异常数据点影响较大,数据可视化效果差,不适于处理数据采集异常率较高的用户电压数据,而t-SNE[19]作为目前最好的非线性概率降维算法之一,受异常数据点影响较小,对高维数据特征保留完好,数据可视化效果好,适用于对低压配电网络中的高维的复杂用户电压数据的降维处理。因此,选择t-SNE算法作为文章所用的数据降维算法。
-
本小节将重点阐述t-SNE算法的原理步骤。首先,计算联合概率以表示各数据点之间的关联性,分别计算条件概率
$ {p_{j|i}} $ 与$ {p_{i|j}} $ ,如式(3)、式(4)所示。$$ {p_{{j}|{i}}} = \dfrac{{\exp \left( {{{ - {{\left\| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right\|}^2}} \mathord{\left/ {\vphantom {{ - {{\left\| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right\|}^2}} {2\sigma _{i}^2}}} \right. } {2\sigma _{i}^2}}} \right)}}{{{\displaystyle \sum\limits}_{k \ne i} {\exp \left( {{{ - {{\left\| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_k}} \right\|}^2}} \mathord{\left/ {\vphantom {{ - {{\left\| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_k}} \right\|}^2}} {2\sigma _{i}^2}}} \right. } {2\sigma _{i}^2}}} \right)} }} $$ (3) $$ {p_{{i}|{j}}} = \dfrac{{\exp \left( {{{ - {{\left\| {{{\boldsymbol{x}}_j} - {{\boldsymbol{x}}_i}} \right\|}^2}} \mathord{\left/ {\vphantom {{ - {{\left\| {{{\boldsymbol{x}}_j} - {{\boldsymbol{x}}_i}} \right\|}^2}} {2\sigma _{j}^2}}} \right. } {2\sigma _{j}^2}}} \right)}}{{{\displaystyle \sum\limits}_{k \ne i} {\exp \left( {{{ - {{\left\| {{{\boldsymbol{x}}_j} - {{\boldsymbol{x}}_k}} \right\|}^2}} \mathord{\left/ {\vphantom {{ - {{\left\| {{{\boldsymbol{x}}_j} - {{\boldsymbol{x}}_k}} \right\|}^2}} {2\sigma _{j}^2}}} \right. } {2\sigma _{j}^2}}} \right)} }} $$ (4) 式中:
xi,xj,xk ——任意3个输入向量;
${\sigma _i}$ ,${\sigma _j}$ ——以xi和xj为高斯分布中心的模型方差。再利用式(5)计算高维数据的联合概率分布
${p_{{ij}}}$ :$$ {p_{ij}} = \dfrac{{{p_{{j}|{i}}} + {p_{{i}|{j}}}}}{{2n}} $$ (5) 式中:
n ——高维输入数据集中高维向量的个数。
接着利用式(6)计算高维数据的联合概率分布
$ {q_{ij}} $ :$$ {q_{ij}} = \dfrac{{{{\exp \left( {- {{\left\| {{\boldsymbol{y}_i} - {\boldsymbol{y}_j}} \right\|}^2}} \right)}}}}{{\sum\nolimits_{k \ne i} {\exp {{\left( {- {{\left\| {{{\boldsymbol{y}}_i} - {{\boldsymbol{y}}_k}} \right\|}^2}} \right)}}} }} $$ (6) 式中:
yi,yj,yk——经过初步降维得到的3个输出向量,此时算法还未收敛。
而满足
${p_{{ij}}} = {q_{{ij}}}$ 这一条件是高低维数据局部特征保留完整、变化差异小的充要条件,因此利用该条件作为算法的目标函数构建条件,利用式(7)来构建目标函数优化${p_{{ij}}}$ 和${q_{{ij}}}$ 之间的$ {\text{KL}} $ 散度:$$ \dfrac{{{\rm{\partial}}{\boldsymbol{C}}}}{{\partial {{\boldsymbol{y}}_{i}}}} = 4\displaystyle \sum\limits_j {\left( {{p_{{ij}}} - {q_{{ij}}}} \right)} \left( {{{\boldsymbol{y}}_{i}} - {{\boldsymbol{y}}_{j}}} \right){\left( {1 + {{\left\| {{{\boldsymbol{y}}_{i}} - {{\boldsymbol{y}}_{j}}} \right\|}^2}} \right)^{ - 1}} $$ (7) 最后筛选出
$ {\text{KL}} $ 散度最小的特征集合${{\boldsymbol{Y}}^T} = \{ {{y_1}, {y_2}, \ldots ,{y_{n}}}\}$ 。算法3.1提供了t-SNE算法的伪代码。算法3.1:t分布随机近邻嵌入方法 输入:高维数据集 ${\boldsymbol{X}} = \left\{ { {x_1},{x_2}, \ldots ,{x_{n} } } \right\}$ ;困惑度$ {\text{Perp}} $ ;学习率$ \eta $ ;迭代次数T;动量${\boldsymbol{\alpha}} \left( t \right)$ 输出:低维数据集 ${{\boldsymbol{Y}}^T} = \left\{ { {y_1},{y_2}, \ldots ,{y_{n} } } \right\}$ 步骤: 1)利用式(3)、式(4)计算在给定 $ {\text{Perp}} $ 下的条件概率$ {p_{j|i}} $ 与$ {p_{i|j}} $ ;2)令联合概率 ${p_{ {ij } } } = \dfrac{ { {p_{ {j}|{i} } } + {p_{ {i}|{j} } } } }{ {2n} }$ ;3)用正态分布 $ N\left( {0,{{10}^{ - 4}}I} \right) $ 随机初始化目标低维数据集${{\boldsymbol{Y}}^0} = \left\{ { {y_1},{y_2}, \ldots ,{y_{n} } } \right\}$ ;4)迭代求解,从t=1到T,执行步骤5)至7); 5)利用式(6)计算低维空间下的联合概率 ${q_{ {ij} } }$ ;6)利用梯度下降法式(7)计算梯度 $\dfrac{ {\partial {\boldsymbol{C}}} }{ {\partial {{\boldsymbol{y}}_{i} } } }$ ;7)对目标低维数据集进行更新 ${ {\boldsymbol{Y} }^{t} } = {Y^{ {t} - 1} } + \eta \dfrac{ {\partial {\boldsymbol{C} } } }{ {\partial {\boldsymbol{Y} } } } + \alpha \left( t \right)\left( { {{\boldsymbol{Y}}^{ {t} - 1} } - {{\boldsymbol{Y}}^{ {t} - 2} } } \right)$ ;8)结束。 -
聚类分析指的是把一个输入数据集按照某种特定的标准度量划分成不同的簇,且在此标准下簇内数据样本差异性低,不同簇之间的数据样本差异性高,最终实现类别划分的功能。对于完成特征降维的低维电压特征数据集而言,其内部特征差异呈现同类小、异类大的特点。因此,选用无监督学习中的聚类算法可以完成对用户数据的分类任务。
-
目前常用的数据聚类算法主要可以分为划分式聚类、密度聚类、层次化聚类等。K均值聚类方法(k-means)是经典划分式聚类算法之一,聚类依据为数据间的欧式距离大小,其优点在于调参简单,计算简便,但聚类精度低,对异常数据较为敏感,无法处理非凸性数据的聚类问题,因此不适于处理用户拓扑种类多样的低维电压特征数据;在层次化聚类方法中,以平衡迭代规约和聚类方法(Balanced Iterative Reducing and Clustering Using Hierarchies,BIRCH)[20]为例,其聚类依据为建立分类树结构按照树的节点一层一层聚类,聚类速度快,但主要缺点在于无法处理非凸性数据的聚类问题,且调参复杂,对同一种情况下的数据集,输入不同的算法参数会有较大的结果差异,加之此聚类算法没有科学的机器调参方法进行聚类效果判据分析,需要进行人工调参,最佳聚类参数需要通过枚举和人工分析求出,工程应用效率低,不适于处理工程应用中的大量台区用户数据;而在密度聚类算法中,应用广泛的DBSCAN[21],其聚类依据为根据已降维的数据密度进行聚类,适于对可视化效果好、密度均匀的凸性或非凸性数据进行聚类分析,与前述中的t-SNE降维算法相容性高,同时有着科学的机器调参方法进行聚类效果判据分析,不需要人工分析最佳的聚类参数,有着较高的工程应用价值,能够精细地处理复杂的数据量大的低维电压特征数据。因此,选择DBSCAN算法作为文章所用的数据聚类算法。
-
DBSCAN算法是最有效的密度聚类算法之一。算法将某一对象的
$ \varepsilon $ 邻域内含大于等于$ {\text{MinPts}} $ 数量的数据点的对象称为核心对象,将某一核心对象与其的$ \varepsilon $ 邻域内的对象间的关系称为密度可达关系。DBSCAN首先会遍历找到所有的核心对象,然后随机选择一个作为种子,找到与其有着密度可达关系的所有样本点集合作为一个聚类簇,循环执行上述步骤,直至所有核心对象都完成归类。最后,算法将少数游离在簇外的异常样本点标记为噪音点,它们不属于任何一个聚类簇,并输出不同数据点的类别结果。由于DBSCAN算法可以轻松识别和过滤掉离群值,因此在密度较大的数据集中表现良好,且不需要预先指定聚类的数量。这使得它成为机器学习领域中非常有用的聚类算法之一。算法3.2提供了DBSCAN算法的伪代码。
算法3.2:基于数据密度的噪声应用空间聚类方法 输入:数据集 ${\boldsymbol{D}} = \left\{ { {p_1},{p_2}, \ldots ,{p_{n} } } \right\}$ ;描述邻域关系参数:邻域半径$ \varepsilon $ ;邻域样本对象密度阈值MinPts输出:聚类簇划分 ${\boldsymbol{C}} = \left\{ { {C_1},{C_2}, \ldots ,{C_{k} } } \right\}$ 步骤: 1)标记D内所有对象为未访问对象; 2)随机选择一个未访问对象pi; 3)标记pi为已访问对象; 4)如果pi的 ${\varepsilon}$ 邻域至少有MinPts个对象,循环执行步骤5)至12),否则跳转执行步骤13);5)创建一个新簇Cj,并把pi添加到簇Cj中; 6)设N是pi的 $ \varepsilon $ 邻域内的样本集合,遍历N中的每个点$ p' $ ;7)如果 $ p' $ 是未访问对象,循环执行步骤8)至11),否则遍历下一个对象;8)标记 $ p' $ 为已访问对象;9)如果 $ p' $ 的$ \varepsilon $ 邻域至少有MinPts个对象,循环执行步骤10)至11),否则跳转执行步骤7);10)把这些数据对象添加到N中; 11)如果 $ p' $ 还不是任何簇的成员,就把$ p' $ 添加到簇Cj中;12)保存簇Cj; 13)标记pi为噪音点; 14)搜寻是否还有未访问的对象,若有: 15)跳转执行步骤2); 16)结束。 -
本章通过对中国海南省三亚市下属3个台区实际数据进行分析,证明在实际工程应用中文章所提方法的有效性。3个实际台区的基础参数如表1所示。
台区 用户数 A相表数量 B相表数量 C相表数量 数据采集完整率/% 1 220 80 74 66 100.0 2 216 72 68 76 94.6 3 233 81 75 77 93.1 Table 1. Basic parameters of the actual low-voltage distribution transformer networks
各台区数据集由所有用户智能电表电压采集数据组成。其中,数据采集长度为3 d,频率为每分钟一次,总共4320个时刻点。
本章首先对台区类别以及各台区下用户相位进行识别,接着将文章所提方法与其他方法进行比较,证明文章所提方法在实际工程领域的有效性。
首先,利用低压配电网络智能电表采集的节点电压数据生成时序电压矩阵U。电压矩阵大小为669×4320,669为3个台区的用户测量点的总和,电压矩阵行向量表示同一智能电表记录的某一用户的电压序列,4320个列向量表示相同时刻下各智能电表测得的电压大小。
接着,对电压矩阵U进行归一化处理,得到标准化时序电压矩阵
$ {{\boldsymbol{U}}'} $ 。然后,采用t-SNE降维算法对该标准化时序电压特征矩阵
$ {{\boldsymbol{U}}'} $ 做降维处理。降维结束后,得到二维的电压特征矩阵${{\boldsymbol{U}} _{{2{\rm{d}}}}}$ 。将
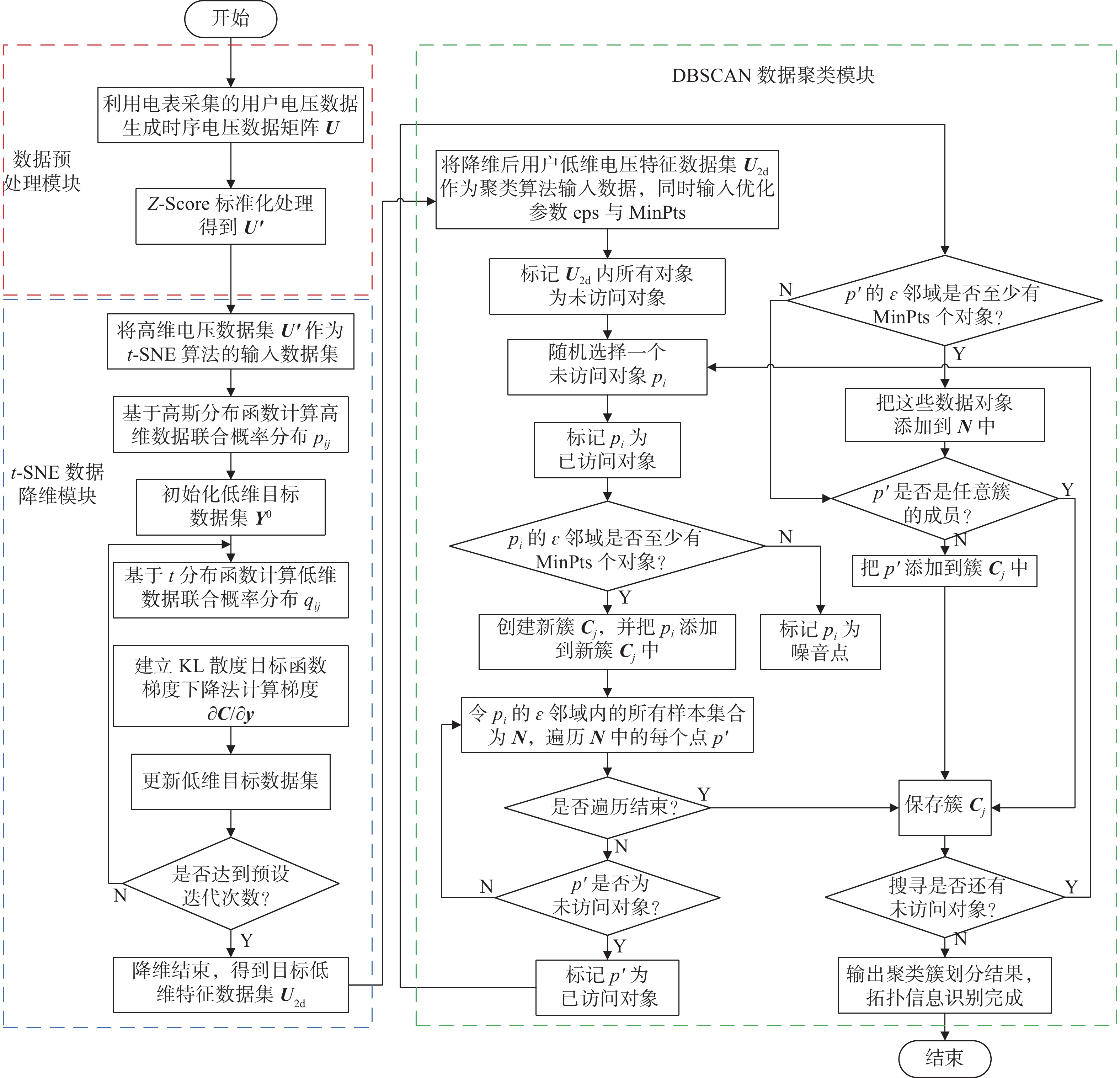
${ {\boldsymbol{U}} _{{2{\rm{d}}}}}$ 作为DBSCAN聚类算法的输入矩阵,采用枚举迭代的方法对距离阈值参数eps与样本数阈值参数min_samples进行机器调参,得出噪声点最小、轮廓系数最大的参数组合,作为DBSCAN聚类算法对该组输入数据矩阵的最佳输入参数。聚类完成后,输出用户的拓扑分类结果,用户拓扑归属关系识别完成。整体方案流程图如图1所示。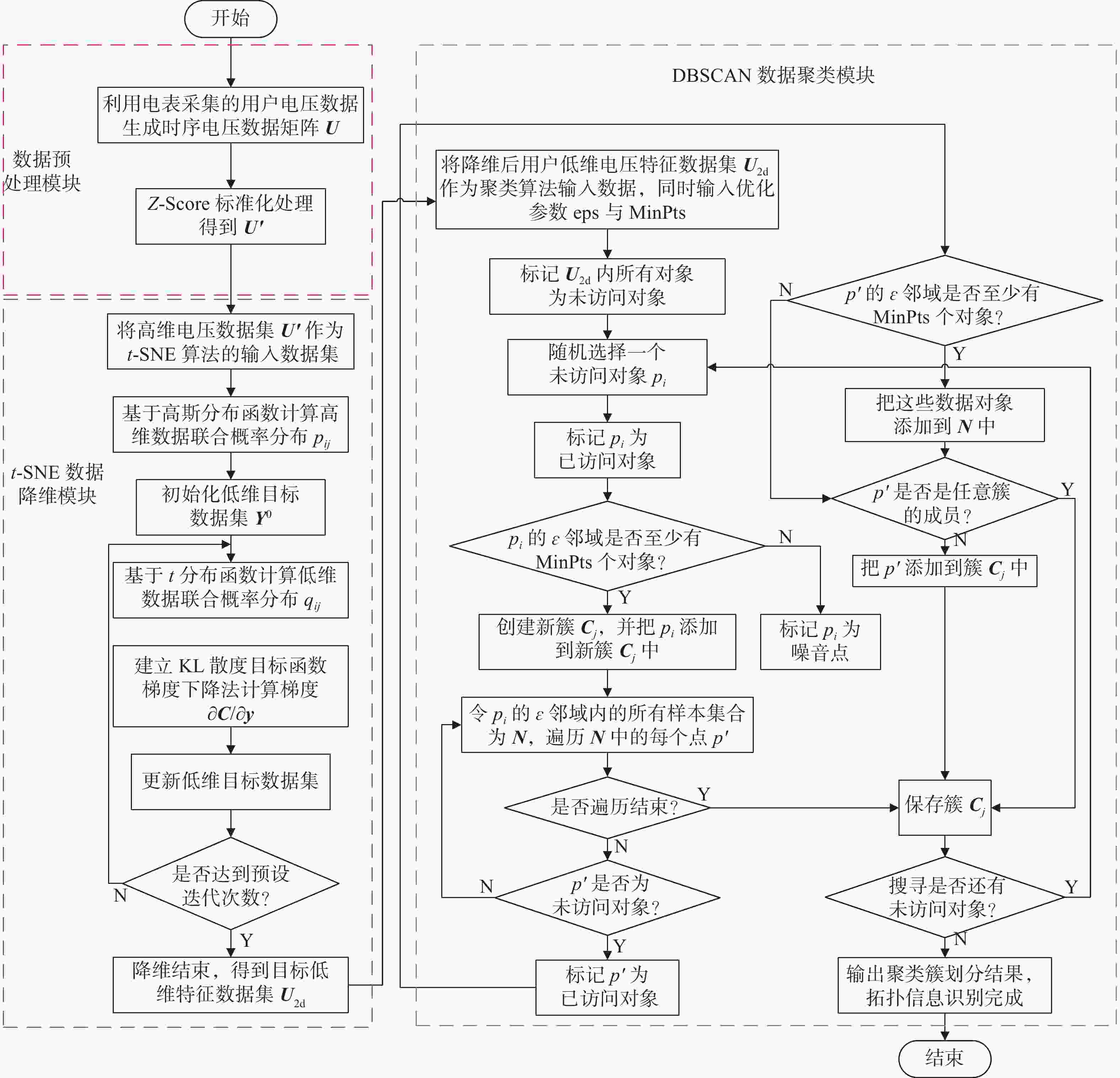
Figure 1. Flowchart of the identification of low-voltage distribution network attribution relationship and phase information
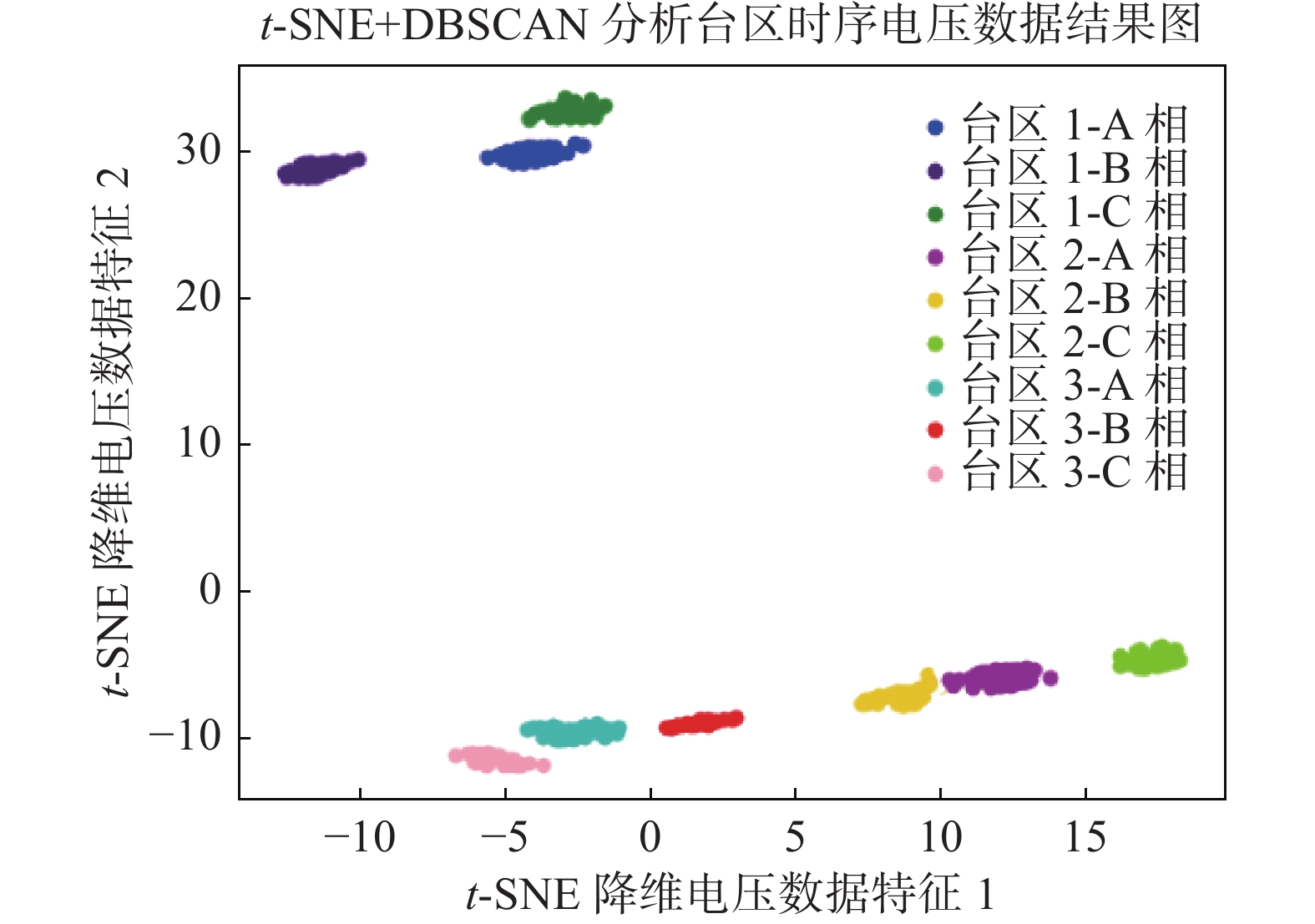
经过详细统计与计算,最终得出低压用户与台区归属关系的识别准确率为100%,不同台区用户相位识别平均准确率为99.1%。聚类识别效果图如图2所示。

Figure 2. Clustering effect diagram of low-voltage distribution network attribution relationship and phase information
为了证明文章所提方法与当前其他主流辨识算法相比具有更高的准确性与普适性,文章从线性降维算法中选用基于距离映射降维的PCA降维法,从流形降维算法中选用基于数据点与点之间流形关系降维的LLE降维法,与文章所提的基于概率映射降维的t-SNE降维法进行对照;从划分式聚类算法中选用基于欧氏距离聚类的k-means聚类法,从层次化聚类算法中选用基于建立分类树结构按照树节点层层聚类的BIRCH聚类法,与文章所提的基于数据密度的DBSCAN密度聚类法进行对照,最终辨识结果准确率如表2所示。
识别算法 台区归属识别准确率/% 用户相位识别准确率/% 台区1 台区2 台区3 A相 B相 C相 t-SNE+DBSCAN 100.0 100.0 100.0 100.0 99.4 98.9 t-SNE+BIRCH 100.0 100.0 100.0 100.0 93.6 94.4 t-SNE+k-means 100.0 100.0 100.0 100.0 91.2 86.9 LLE+DBSCAN 99.0 96.5 98.8 76.3 78.6 75.6 LLE+BIRCH 96.5 95.7 91.5 73.1 69.5 68.0 LLE+k-means 93.6 94.0 90.6 72.5 63.1 62.0 PCA+DBSCAN 96.5 94.1 97.6 70.8 69.0 69.2 PCA+BIRCH 96.2 93.7 91.2 69.6 68.7 64.0 PCA+k-means 92.0 91.7 92.1 63.1 59.5 61.8 Table 2. Identification accuracy of low-voltage distribution network attribution relationship and phase information under different methods
分析表2数据可知,对于实际台区中的用户时序电压数据,在采用相同的降维算法的情况下,DBSCAN算法相较于BIRCH算法与k-means算法在聚类数据上有着更高的台区归属关系识别准确率与相位识别准确率;在采用相同的聚类算法的情况下,t-SNE算法相较于LLE算法与PCA算法有着更高的识别准确率。
其主要原因在于由智能电表采集的用户电压数据体量大、拓扑信息复杂数据簇分支多、精度较低噪点多,从算法原理的角度来看,PCA算法泛化能力差,LLE算法与k-means算法易受数据噪点影响,BIRCH算法仅擅长处理树形数据,在处理该类数据时的效果不如泛化性强、数据可视化效果好的t-SNE算法与擅长处理密度均匀数据的DBSCAN算法。
因此,分别结合在两方面表现最优的算法,即t-SNE+DBSCAN的组合,能够解决实际情况下含噪点用户数据的台区归属辨识问题以及多台区下用户相序辨识问题,证明了文章所提方法的有效性与优势性。
-
对文章的研究内容总结如下:
1)提出了一种基于密度聚类的低压台区归属关系及相位识别新方法,该方法改进了已有的数据预处理方法、降维算法和聚类算法,将3种方法有机地结合在一起用于拓扑信息识别问题上,为低压台区拓扑信息的识别提供了不一样的研究思路。
2)经过严谨的实验分析和比较,结果表明,所提出的方法能够很好地利用智能电表采集的含噪声的实际工程电压数据,在识别台区归属信息与相位信息问题上能够达到95%以上的准确率,并高于现有的其他主流识别算法,证明了文章所提方法在解决此类问题上具有有效性与优势性。
但文章所提方法仍具有一定的局限性,体现在基于概率降维的t-SNE降维方法无法保留原始高维数据的流形信息,即降维后的数据点图无法保留分支与分支之间和用户与用户之间的电气距离信息,无法对低压台区的拓扑信息进行更深入准确的识别。下一阶段将探索更有效的深度学习方法,针对低压台区用户分支的电气距离识别问题作进一步的研究。
Identification of Low-Voltage Distribution Network Attribution Relationship and Phase Information Based on Density Clustering
doi: 10.16516/j.gedi.issn2095-8676.2023.05.018
- Received Date: 2023-03-22
- Accepted Date: 2023-05-08
- Rev Recd Date: 2023-05-04
- Available Online: 2023-09-06
- Publish Date: 2023-09-10
-
Key words:
- low-voltage distribution network /
- voltage data information /
- t-SNE /
- DBSCAN /
- identification of low-voltage distribution network attribution relationship /
- phase identification
Abstract:
| Citation: | YAN Donghui. Identification of Low-Voltage Distribution Network Attribution Relationship and Phase Information Based on Density Clustering[J]. SOUTHERN ENERGY CONSTRUCTION, 2023, 10(5): 149-156. doi: 10.16516/j.gedi.issn2095-8676.2023.05.018 |



































































 DownLoad:
DownLoad: