-
实现“碳达峰”和“碳中和”是当今国际社会能源发展已达成的共识,我国近期提出“双碳”目标,2030年风电、太阳能总装机容量将达到1.2 GW以上[1]。对我国而言,改变以煤炭为主的高碳能源电力结构转型为以清洁能源为主的新型电力系统是实现可持续发展的必由之路,推动能源低碳转型,关键是加快发展风电、太阳能等新能源。
随着新能源的快速发展,电力系统呈现“双高”特征,新能源出力的波动性、间歇性和随机性给电网规划及运行带来新的挑战。研究新能源出力特性是一项重要工作,已有学者从不同角度进行研究。在风电特性的分析方面,文献[2]用风电出力变化率等指标表征风电自然特性,用风电穿透率、风电调峰特性指标等指标描述风电与电网交互影响。文献[3]用峰谷时段风电出力中位数差反映风电调峰特性。在光伏特性分析方面,文献[4]提出用“光伏出力季节属性”“平均出力”和“全日最大出力”3个指标来评估光伏出力特性。文献[5]提出3种概率性负荷特性指标,用蒙特卡洛模拟法评估不同渗透率的光伏接入对配电网负荷特性的影响。在新能源特性的综合评估方面,文献[6]提出来表征新能源的年特性、季特性及日特性的指标。文献[7]提出由净负荷时序爬坡功率与机组爬坡功率阈值之差作为灵活性需求指标来定量描述新能源波动对电网的影响。文献[8]用时间序列的方法分析新能源-负荷特性,用源荷相似性距离描作为新能源-负荷特性指标描述电力曲线特征。从时间尺度的研究方面,文献[9]基于不同时间尺度分析风电波动特性,在日时间尺度提出六种风电典型波动类型划分方法。文献[10]基于光伏电站运行数据,分析了不同时间尺度的光伏出力波动特性。从实际数据的分析研究方面,文献[11-12]分别对江苏和青海的风电场和光伏电站实际出力特性进行统计分析。文献[13-14]分别分析了内蒙古新能源和湖南新能源对电网的调峰影响。
然而,上述研究虽各有重点,但没有聚焦于多维度、多尺度综合评估新能源与电网的交互影响,有些评估指标和方法有着严谨的理论基础,但很难大规模应用于评估全网的计算,例如蒙特卡洛法[5]要提高指标精度需计算大量抽样样本,计算时间长,收敛速度慢;时间序列法[8]需逐条对两条时间序列进行对比分析,应用场景相对局限。对于电力系统从业人员更关心新能源对电网的影响,以及简明、直观、可利用性强的指标用于实际计算和特性分析。
鉴于以上分析,文章从电网规划和运行的实际工作需求出发,构建评估新能源对电网影响的指标评估体系,提出4类指标即表征电网关键时刻新能源出力特性指标,新能源电量指标,调峰特性指标和灵活性指标,适用于从不同时间尺度评估不同场景新能源对电网的影响,可推广应用于新能源输电规划、接入系统,储能规划等实际工程中,对电网的安全稳定运行提供指标参考。
-
新能源的低碳、清洁特性成为驱动能源转型的关键力量,但其不确定性对电力系统平衡、调峰调频等带来新的挑战,因此不能脱离电网独立分析新能源特性,只有深入分析新能源在“源网荷”背景下的运行特性,才能保证源网荷协调发展,有助于优化新能源配置、新能源消纳和电网的安全稳定运行。
新能源对电网的影响从横向上看有电力平衡、电量平衡、调峰及调频影响,从纵向上看需评估上述影响因子在不同时间尺度上的评价效果。
在分析地区新能源消纳能力时,对地区电网影响最严重的时刻往往是负荷高峰与低谷时段的新能源出力,需应用这些典型场景的新能源出力系数进行电力平衡与调峰计算,即需要建立新能源与负荷相关的出力特性指标;评估地区新能源消纳水平时,弃风弃光率是衡量新能源利用率的重要指标,研究新能源出力与电量的关系对新能源规划尤为重要,即需要建立新能源电量特性指标;在地区调峰特性分析中,需要评估调峰最严峻时段和调峰需求,来相应提出调峰措施,保障电网安全运行,即需要建立反映反调峰特性的指标;在电力系统稳定性评估中,由于新能源的波形特性,系统需要有应对波动与不确定性的调节手段和资源,即需要建立量化灵活性需求的特性指标。
由于具有随机波动特征的新能源发展迅速,新型电力系统在不同时间尺度上的特性是变化的。在传统电源规划中,往往以年为规划时间分辨率,而在新型电力系统中则需要考虑多时间尺度多场景的电力平衡分析;在电网实际运行中,需要以月、周为时间分辨率对一年、数年的机组检修、燃料储备、水量分配以及长期交易进行安排;以小时为分辨率对一周、一天的开机方式和出力水平进行优化[15],因此研究不同时间尺度的新能源特性是适应新型电力系统发展要求的。
综上所述,从新能源及负荷的实际运行数据中挖掘出电网规划及运行所需要的、适应多场景应用的表征指标是非常必要的,新能源随机性、间歇性、波动性等不确定特征适用于用概率论研究[16-17],宜采用概率性指标。
-
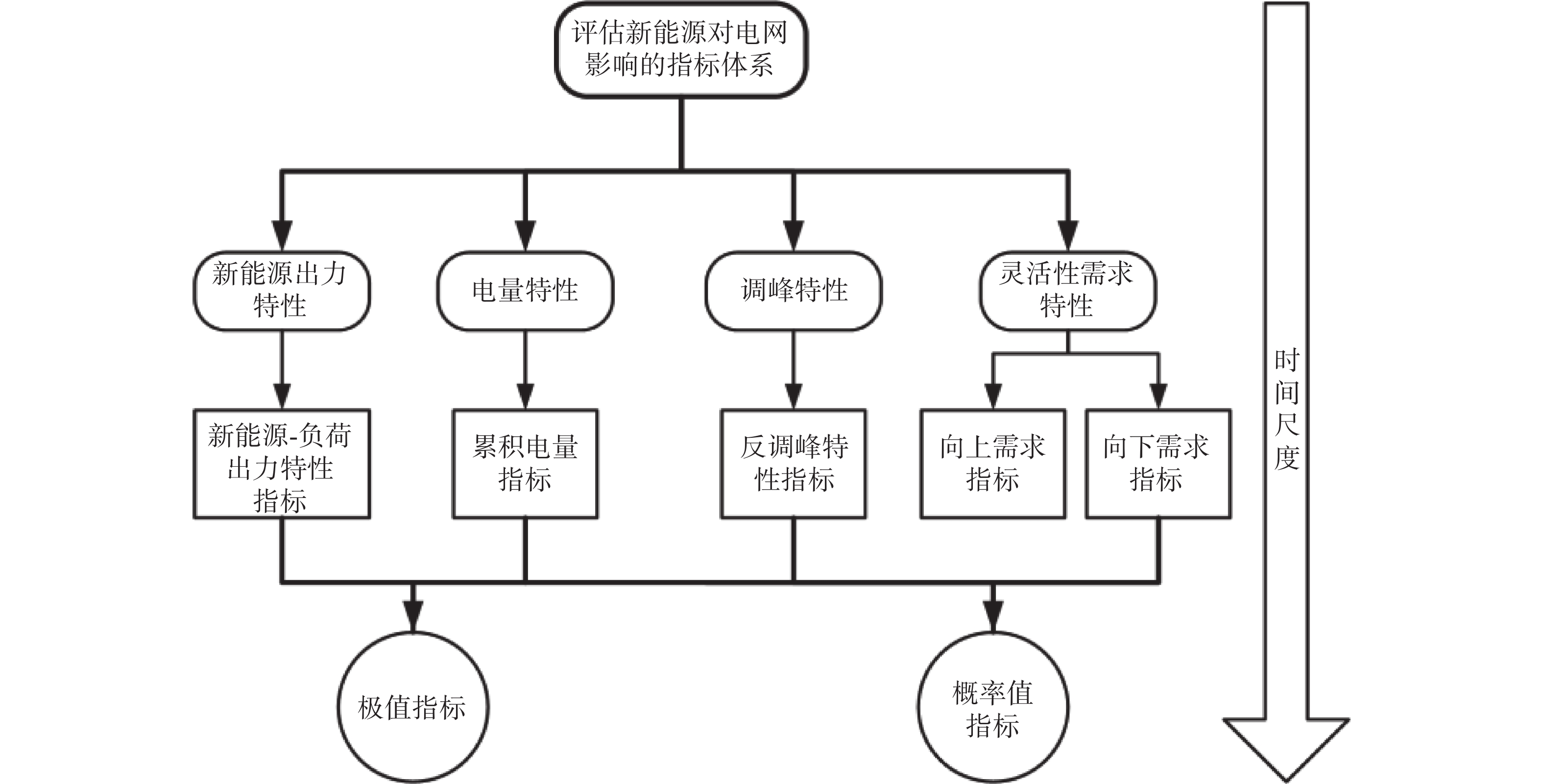
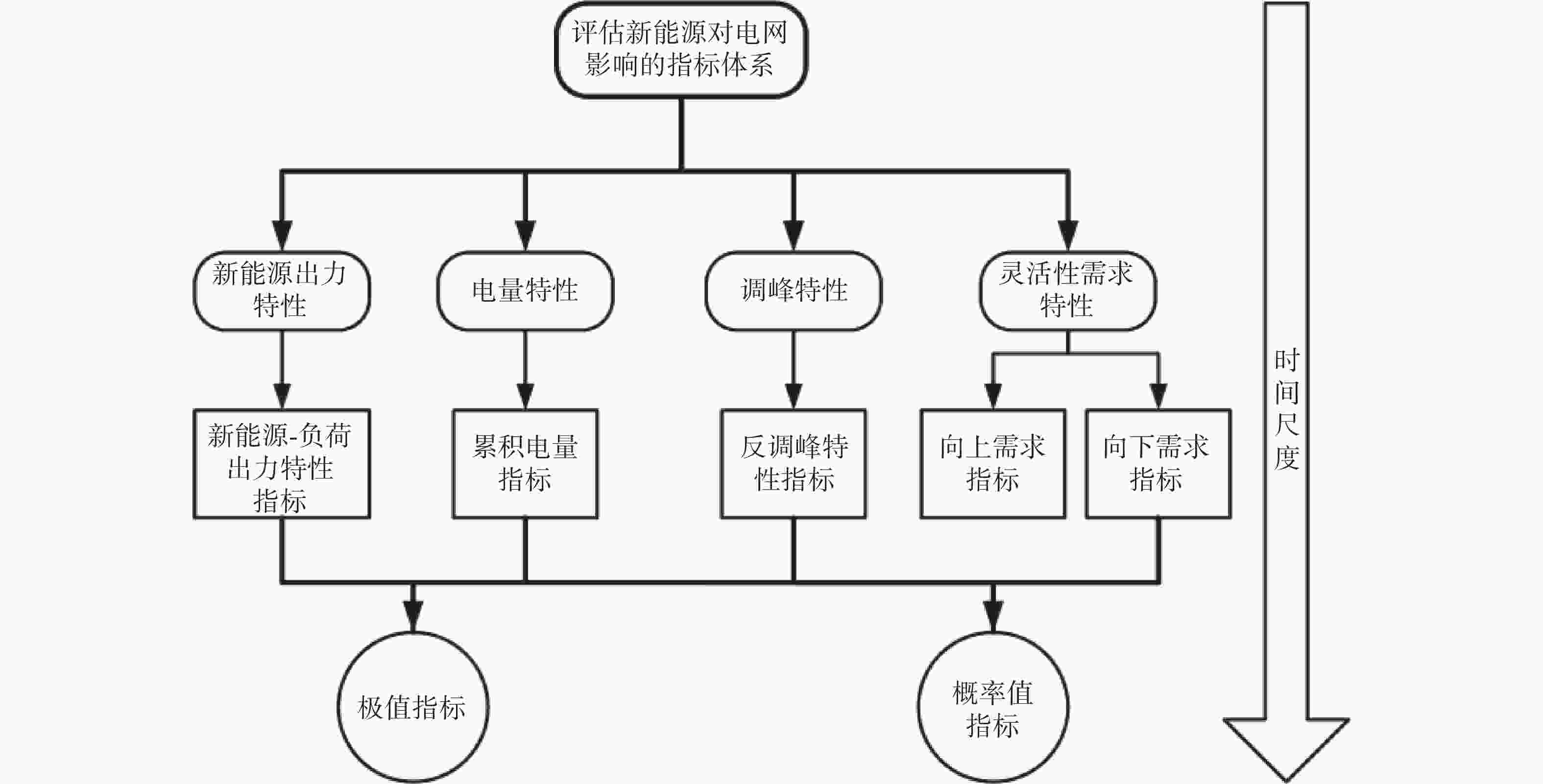
文章提出的评估新能源对电网影响指标分为4类,分别为出力特性、电量特性、调峰特性和灵活性需求特性;每类指标可以用极值、概率值等统计指标来计算,并根据场景需求按分钟、小时、月、年等不同的时间尺度来处理数据。文章提出的指标评估体系详见图1。
-
新能源在电网负荷特殊时段上的出力特性对电网具有典型意义,特别是峰谷时段对调峰和平衡均有较大影响,将源-荷作为整体分析,进一步认识其特性,有助于实现源荷互动,提高对新能源的高效利用。
用LDP、LNP、LV表征在午高峰、晚高峰和低谷负荷下新能源出力指标,每类指标含Cmax、Cmin、C95max和C95min,分别表示该时段的最大值、最小值和95%置信出力值。置信出力是指在一定概率下新能源的保证出力,通常置信度按95%,C95max指标表示新能源出力系数小于等于该值的概率为95%,即95%概率下的最大出力;C95min指标表示新能源出力系数大于等于该值的概率为95%,即95%概率下的保证出力。上述指标均采用新能源出力系数占比来表示,即用新能源出力与装机的比值来标幺化处理作为衡量的统一尺度。
以午时段LDP指标为例,极值指标公式为:
$$ C_{\max } = \mathop {\max }\limits_{t \in T} \dfrac{{{N_t}}}{{{E_t}}} $$ (1) $$ C_{\min } = \mathop {\min }\limits_{t \in T} \dfrac{{{N_t}}}{{{E_t}}} $$ (2) 式中:
Nt ——t时刻的新能源出力(MW);
Et ——t时刻的新能源装机(MW);
T ——计算选取的时间段即午高峰时段。
以午时段LDP指标为例,概率指标公式为:
$$ {{=C}}_{t}=\dfrac{{N}_{t}}{{E}_{t}},{{\boldsymbol{C}}}=\{{C}_{1},{C}_{2},\cdots,{C}_{n}\} $$ (3) $$ {L_{\max }} = {\rm{Ceil}}(n \times 95\% ) $$ (4) $$ {L_{\min }} = \max \{ {\text{floor}}[n \times (1 - 95\% )],1\} $$ (5) $$ {C_{95\max }} = {C_{{L}\max }} $$ (6) $$ {C_{95\min }} = {C_{{L}\min }} $$ (7) 式中:
Ct ——t时刻的新能源出力系数;
C ——对午高峰时段的新能源出力系数序列按从小到大进行排序的数列;
n ——统计时段的样本数;
Ceil(·) ——向上取整;
floor(·) ——向下取整;
L ——相应保证率对应在数列中的位置。
-
通过分析新能源不同出力区间对电量的贡献率来研究不同出力对电网的影响,用Q95指标表征累计电量达到95%对应的新能源出力系数,一般来讲新能源利用率达到95%为国际先进水平[18],因此选取95%作为计算指标依据。该指标在实际应用中可用来表征95%消纳率下对应的新能源的有效容量,可用于新能源送出网架校核等,也可根据各地区实际情况和近远景要求,设置合适的消纳率。
Q95指标公式如下:
$$ {W_j} = \displaystyle \sum\limits_{i = 1}^{{N_j}} {{W_i}} $$ (8) $$ {W_{kj}} = \dfrac{{{W_j}}}{Q} $$ (9) $$ {Q_{kj}} = \displaystyle \sum\limits_{m = 1}^j {{W_{kj}}} $$ (10) $$ {Q}_{95}=j,\text{if}{Q}_{kj}\geqslant 0.95\&{Q}_{kj-1} < 0.95 $$ (11) 式中:
Wj ——第j区间对应的总电量(kWh);
Nj ——将新能源按出力系数划分为m个区间,Nj为第j区间对应的样本数;
Wkj ——第j个区间电量占总电量的比例;
Q ——统计时段总电量(kWh);
Qkj ——第一个区间到第j个区间的累计电量占比。
-
新能源的大规模接入使得电网的调峰面临巨大挑战,特别是负荷低谷时段新能源反而大发即“反调峰特性”对电网的影响更甚,影响地区新能源的消纳、储能的配置等方面,反调峰特性反映为新能源接入后系统的峰谷差增大。净负荷为将新能源出力当作负的负荷与实际负荷叠加,用净负荷峰谷差能反映新能源出力的波动对地区电网调峰影响。若净负荷峰谷差较原始峰谷差变大,说明新能源对电网有反调峰作用。
用KNeg表示最大反调峰比,用P+Neg、P −Neg和P0Neg分别表示正调峰概率、反调峰概率和平调峰概率,用净负荷的峰谷差变化来计算上述指标,具体为:
$$ {K_{{\rm{Neg}}}} = \mathop {\min }\limits_{t \in T} \left( {\dfrac{{{D_t} - D_t^{'}}}{{{D_t}}}} \right) $$ (12) $$ N_{{\rm{Neg}}}^ + = \left\{ {\begin{array}{*{20}{c}} {1,{\text{ if }}{D_t} - D_t^{'} > 0} \\ {0,{\text{ if }}{D_t} - D_t^{'} \leqslant 0} \end{array}} \right. $$ (13) $$ P_{{\rm{Neg}}}^ + = \dfrac{1}{N}\displaystyle \sum\limits_{t = 1}^N {N_{{\rm{Neg}}}^ + } $$ (14) $$ N_{{\rm{Neg}}}^ - = \left\{ {\begin{array}{*{20}{c}} {1,{\text{ if }}{D_t} - D_t^{'} < 0} \\ {0,{\text{ if }}{D_t} - D_t^{'} \geqslant 0} \end{array}} \right. $$ (15) $$ P_{{\rm{Neg}}}^ - = \dfrac{1}{N}\displaystyle \sum\limits_{t = 1}^N {N_{{\rm{Neg}}}^ - } $$ (16) $$ N_{{\rm{Neg}}}^0 = \left\{ {\begin{array}{*{20}{c}} {1,{\text{ if }}{D_t} - D_t^{'} = 0} \\ {0,{\text{ if }}{D_t} - D_t^{'} \ne 0} \end{array}} \right. $$ (17) $$ P_{{\rm{Neg}}}^0 = \dfrac{1}{N}\displaystyle \sum\limits_{t = 1}^N {N_{{\rm{Neg}}}^0} $$ (18) 式中:
Dt ——第t天的原始峰谷差(MW);
D't ——第t天的净负荷峰谷差(MW);
N+Neg ——正调峰,对系统调峰有正面;
N −Neg——负调峰,对系统调峰有反作用;
N0Neg ——平调峰,对系统调峰没有作用;
T ——计算选取的时间段;
N ——T时间段的天数。
-
随着大量新能源接入电网,新能源与负荷波动性叠加,需综合分析新系统下波动性的影响,系统需对负荷与电源的波动进行快速响应,评估系统的灵活性需求,保障电力系统安全可靠运行。系统波动性特征具有向上、向下的方向性和多时间尺度,且不同灵活性资源的响应能力与时间具有较强的相关性[19-20]。
用R+max,R−max分别表征不同时间尺度下灵活性需求的最大向上调率和向下调率,具体如下:
$$ \left\{ {\begin{array}{*{20}{c}} {{R_{{\text{flex + }}}} = \dfrac{{P_{t + 1}^{'} - P_t^{'}}}{{{P_{\max }}}},{\text{ }}P_{t + 1}^{'}- P_t^{'} > 0} \\ {{R_{{\text{flex − }}}} = \dfrac{{P_{t + 1}^{'} - P_t^{'}}}{{{P_{\max }}}},{\text{ }}P_{t + 1}^{'} - P_t^{'} < 0} \end{array}} \right. $$ (19) $$ \left\{ {\begin{array}{*{20}{c}} {R^+_{{\text{max}}} = \mathop {\max }\limits_{t \in T} {R_{{\text{flex + }}}}} \\ {R^-_{{\text{max}}} = \mathop {\min }\limits_{t \in T} {R_{{\text{flex − }}}}{\text{ }}} \end{array}} \right. $$ (20) 式中:
P't+1 ——第t+1时刻净负荷(MW);
P't ——第t时刻净负荷(MW);
Pmax ——T时段最大负荷(MW);
R+flex——灵活性需求向上调率;
R−flex——灵活性需求向下调率。
-
文章结合某地区新能源及电网数据给出文章所提的指标体系的两种算例分析,一是以表形式给出文章指标的计算结果,直观分析地区特性;二是以图形式给出文章所提指标的分布特性,来全面分析不同尺度下地区的新能源特性对电网的影响。
本小节以华东某地区2021年光伏、风电及负荷实际数据进行统计分析,数据采样步长为15 min。该地区从年负荷特性上看,负荷高峰一般在夏冬两季,春秋季是负荷低谷时期;从日负荷特性上看,一般呈现午高峰和晚高峰两个高峰时段,夜间2:00-5:00时为负荷低估时段。
-
地区风电及光伏出力特性指标如表1和表2所示,风电在3个典型时段最大值都比较大,说明风电的随机性更强,相对而言晚高峰和低谷风电极值和保证出力要大于午高峰。
指标/p.u. LDP LNP LV Cmax 0.768 0.850 0.840 Cmin 0.000 0.000 0.000 C95max 0.490 0.537 0.550 C95min 0.006 0.023 0.030 Table 1. Wind power output characteristics index
指标/p.u. LDP LNP LV Cmax 0.720 0.209 0.341 Cmin 0.014 0.000 0.000 C95max 0.637 0.120 0.128 C95min 0.068 0.000 0.061 Table 2. Photovoltaic power output characteristics index
光伏最大出力发生在午高峰,其他两个时段光伏最大值和保证出力值明显小于午高峰。
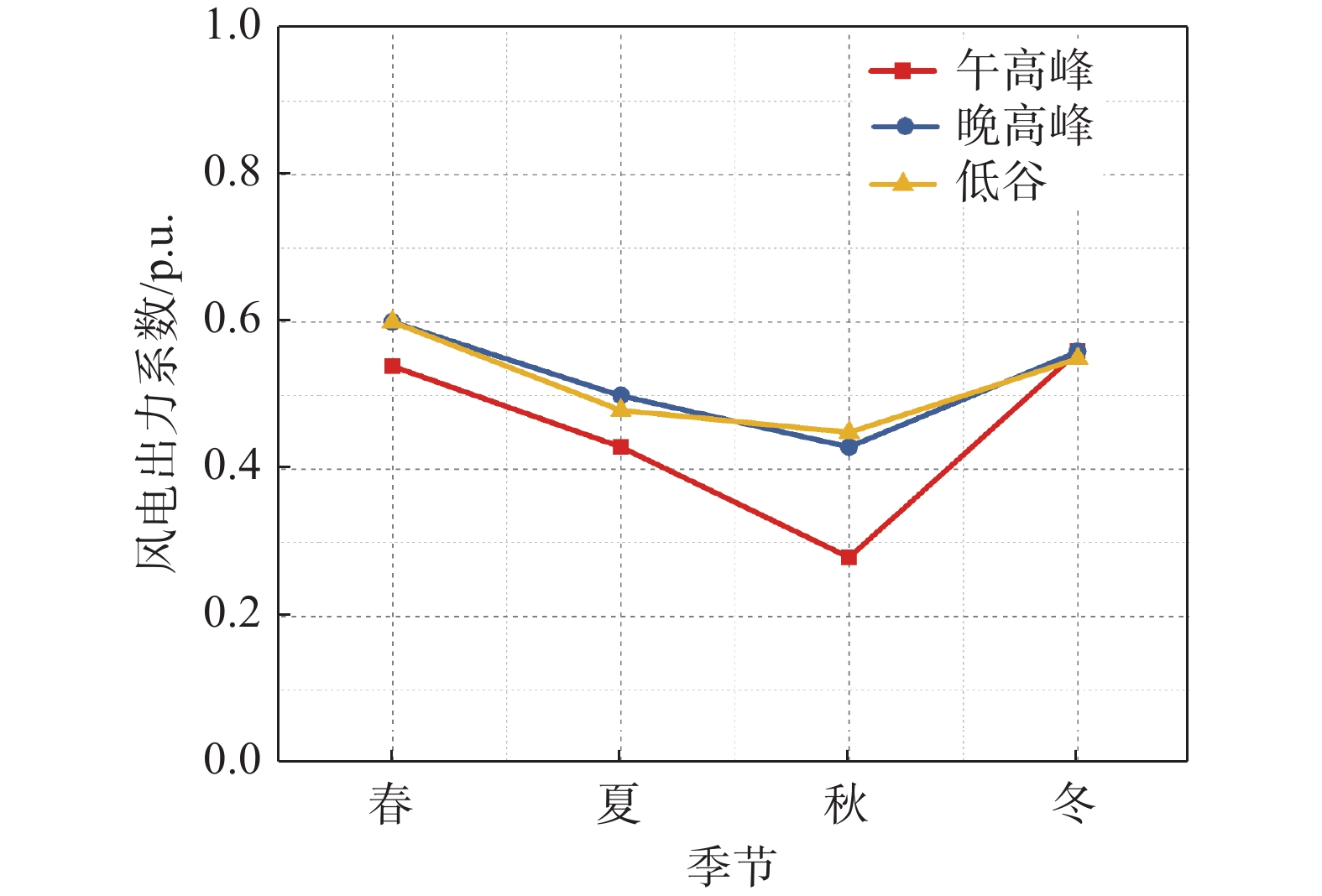
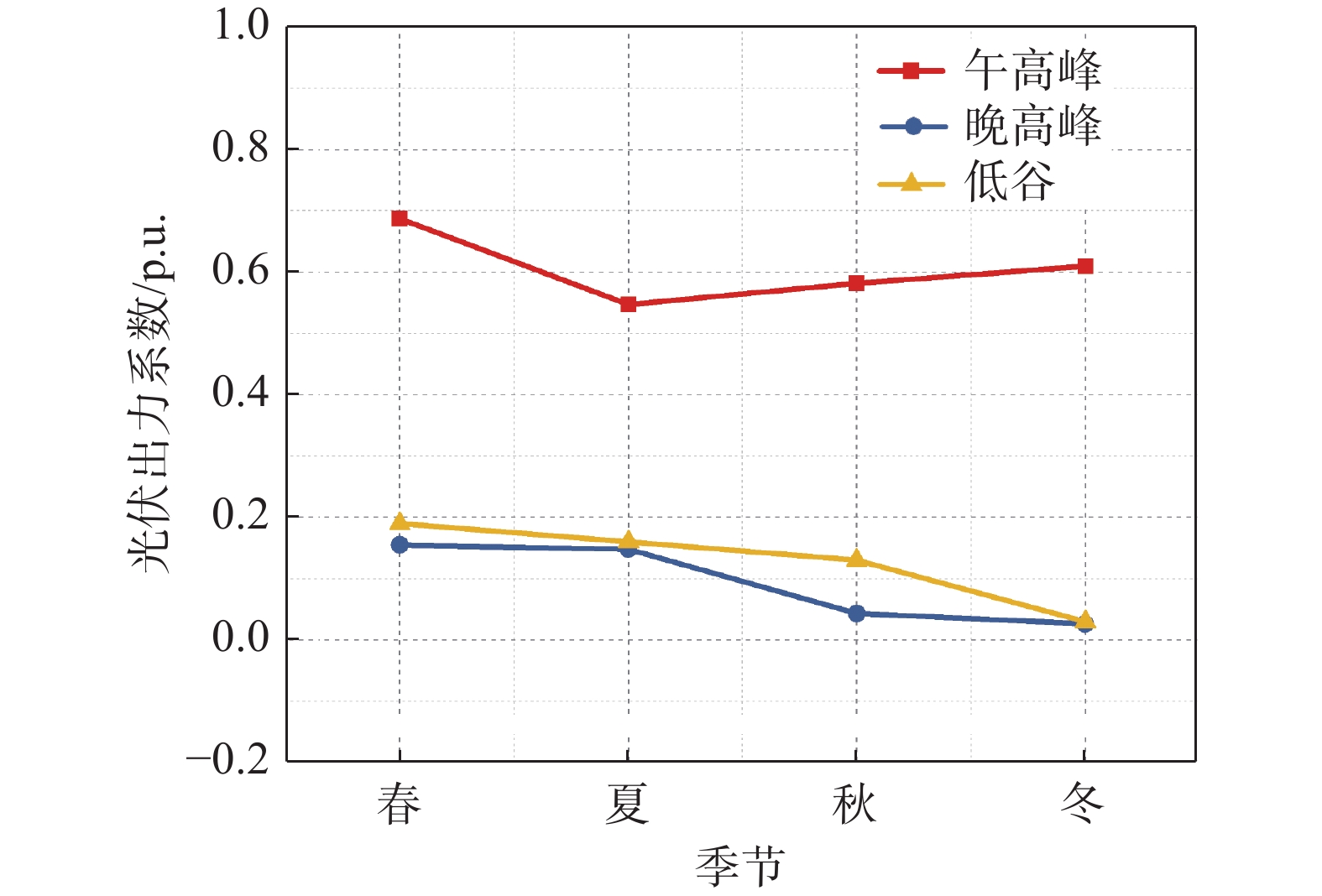
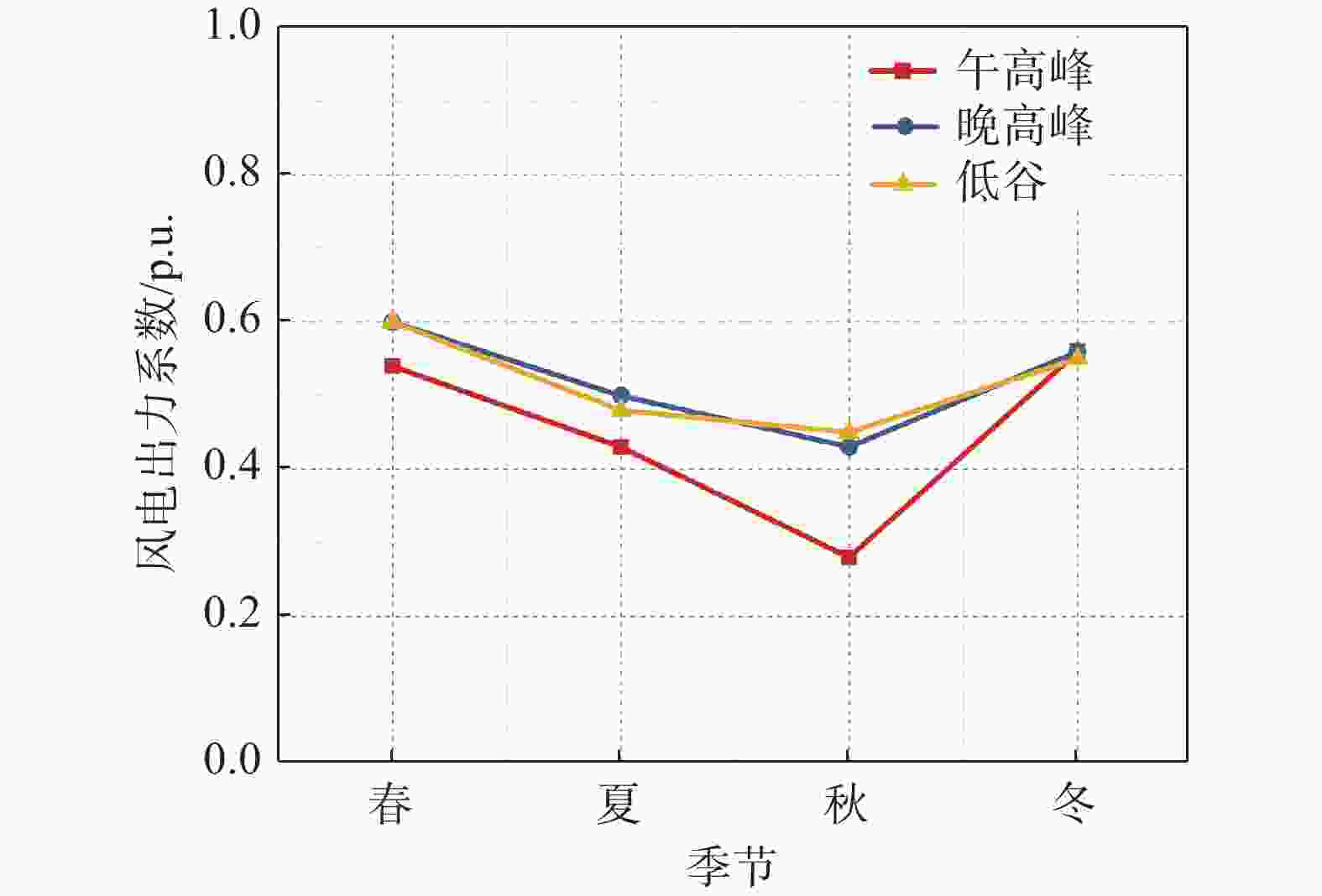
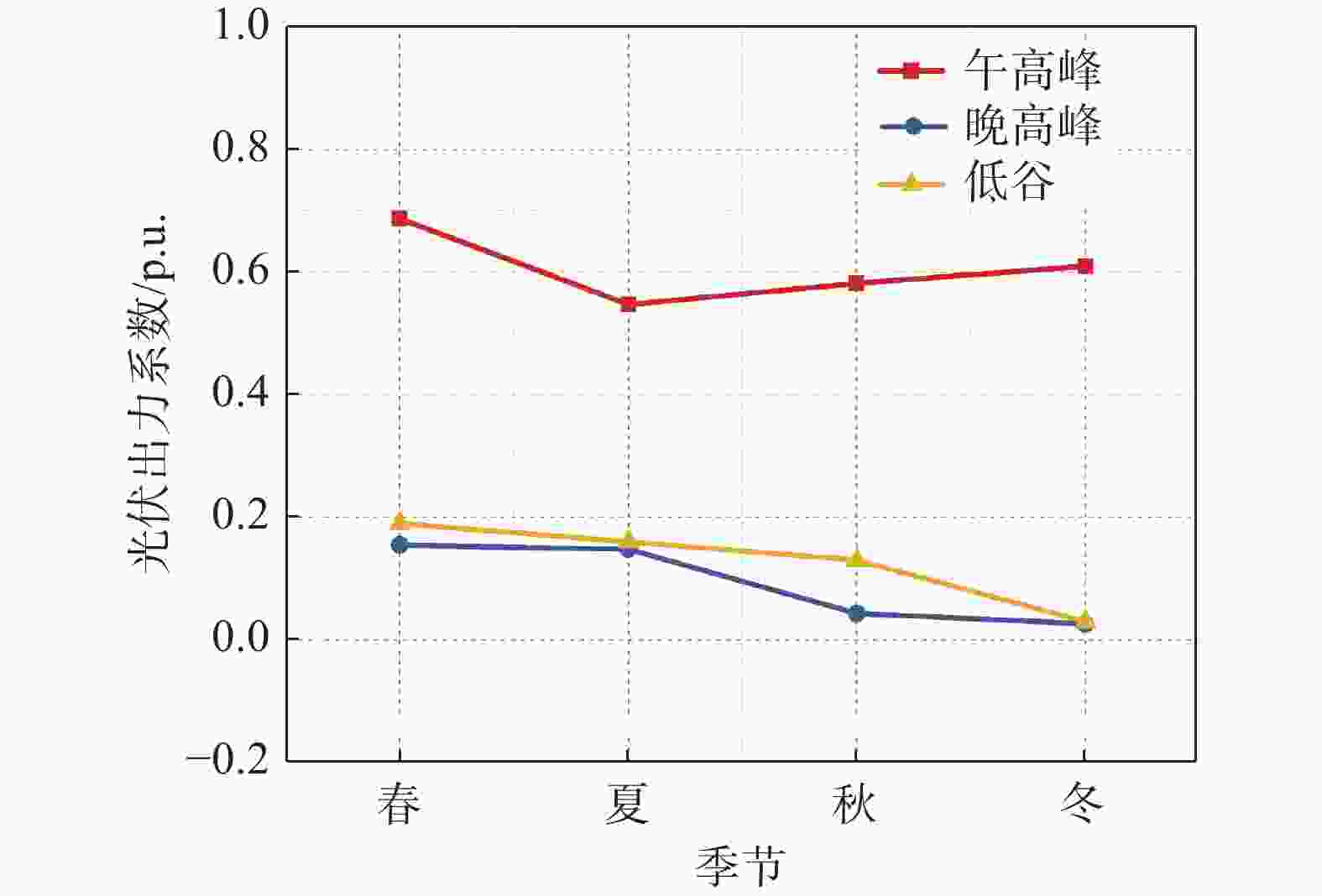
地区风电及光伏的C95max指标季特性分布如图2和图3所示,风电在各季尺度上呈现较为一致的趋势,均是秋季指标较小;该地区光伏在春季午高峰较其他季节大,晚高峰和低谷时冬季光伏较其他季节小。
-
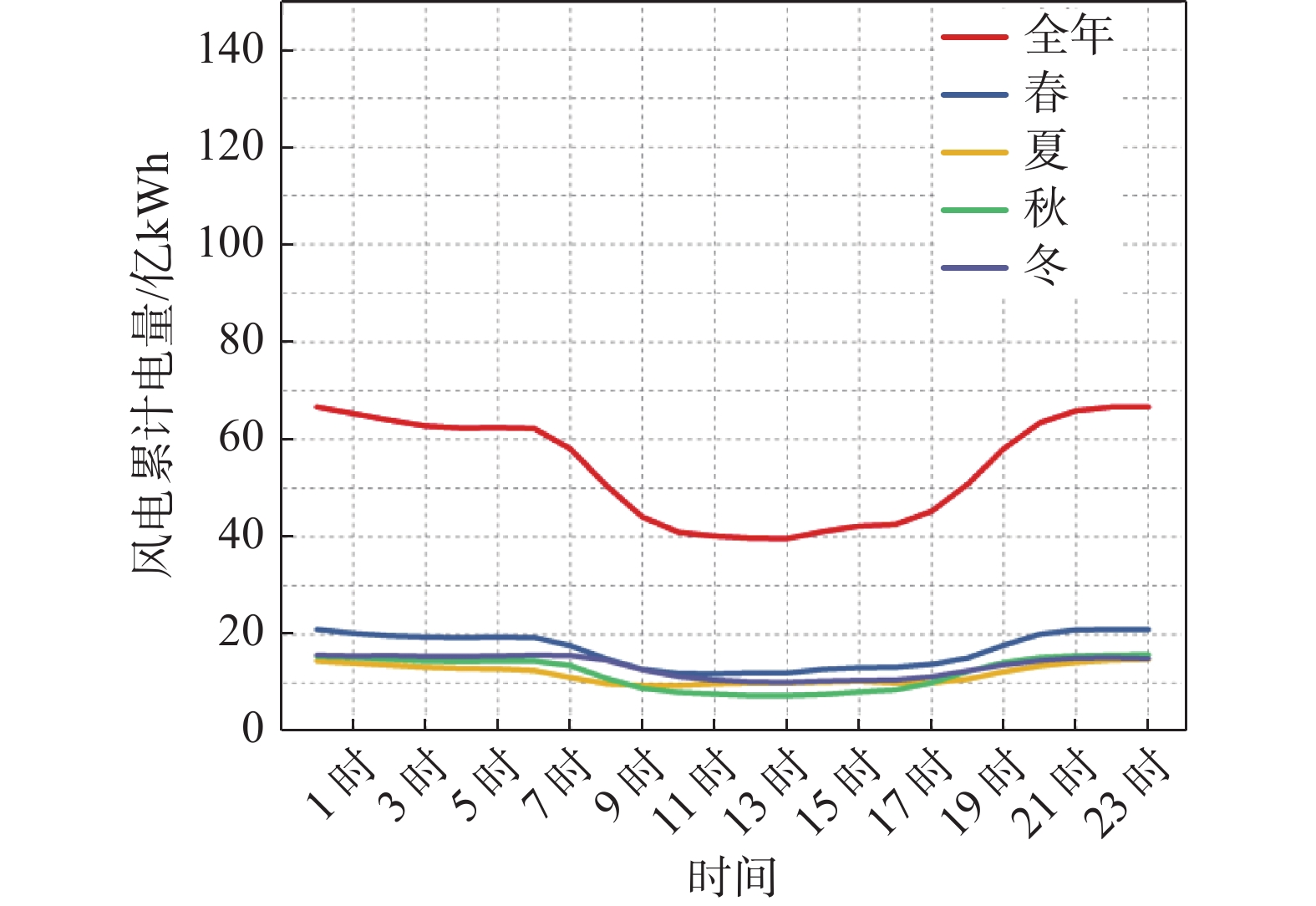
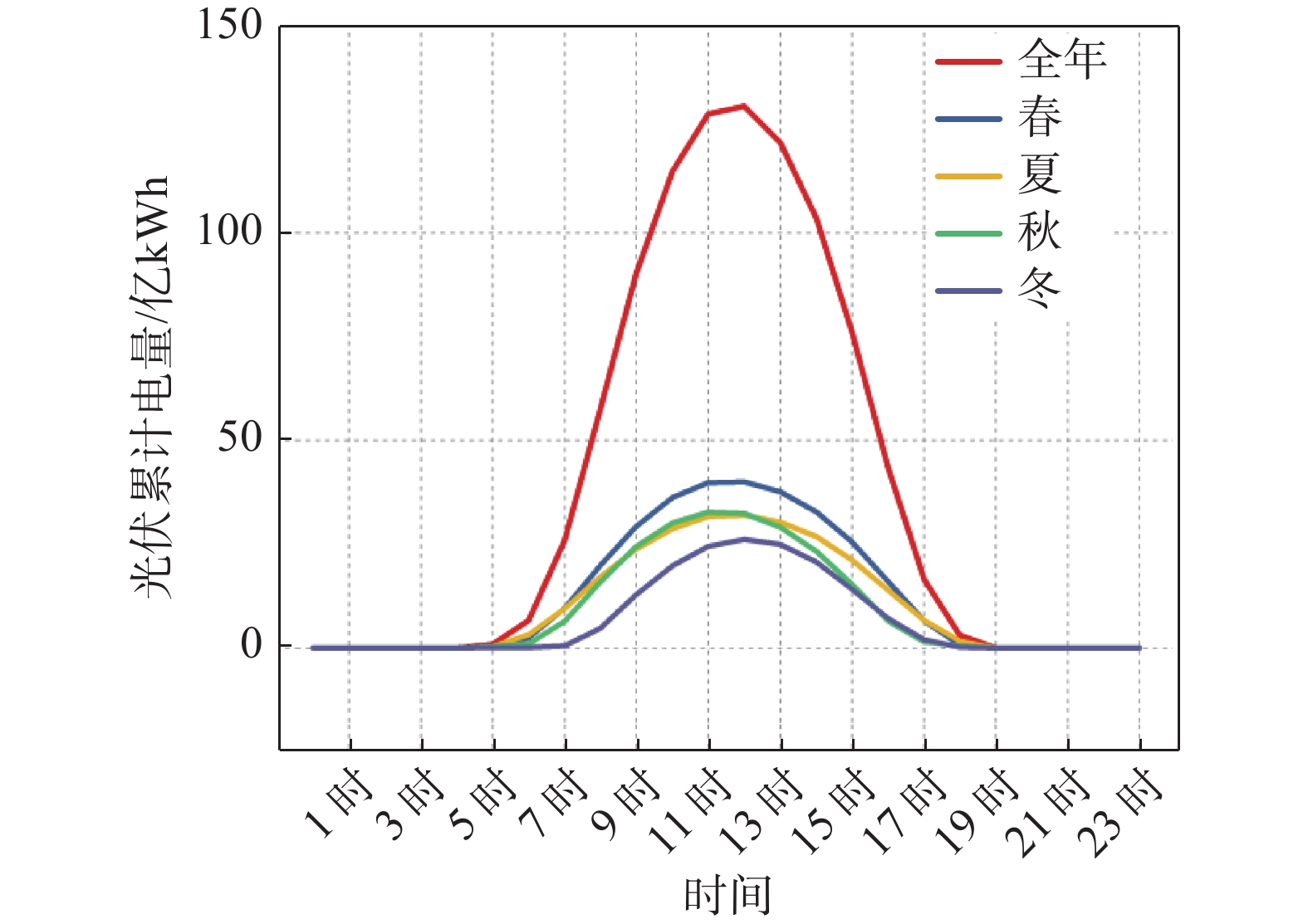
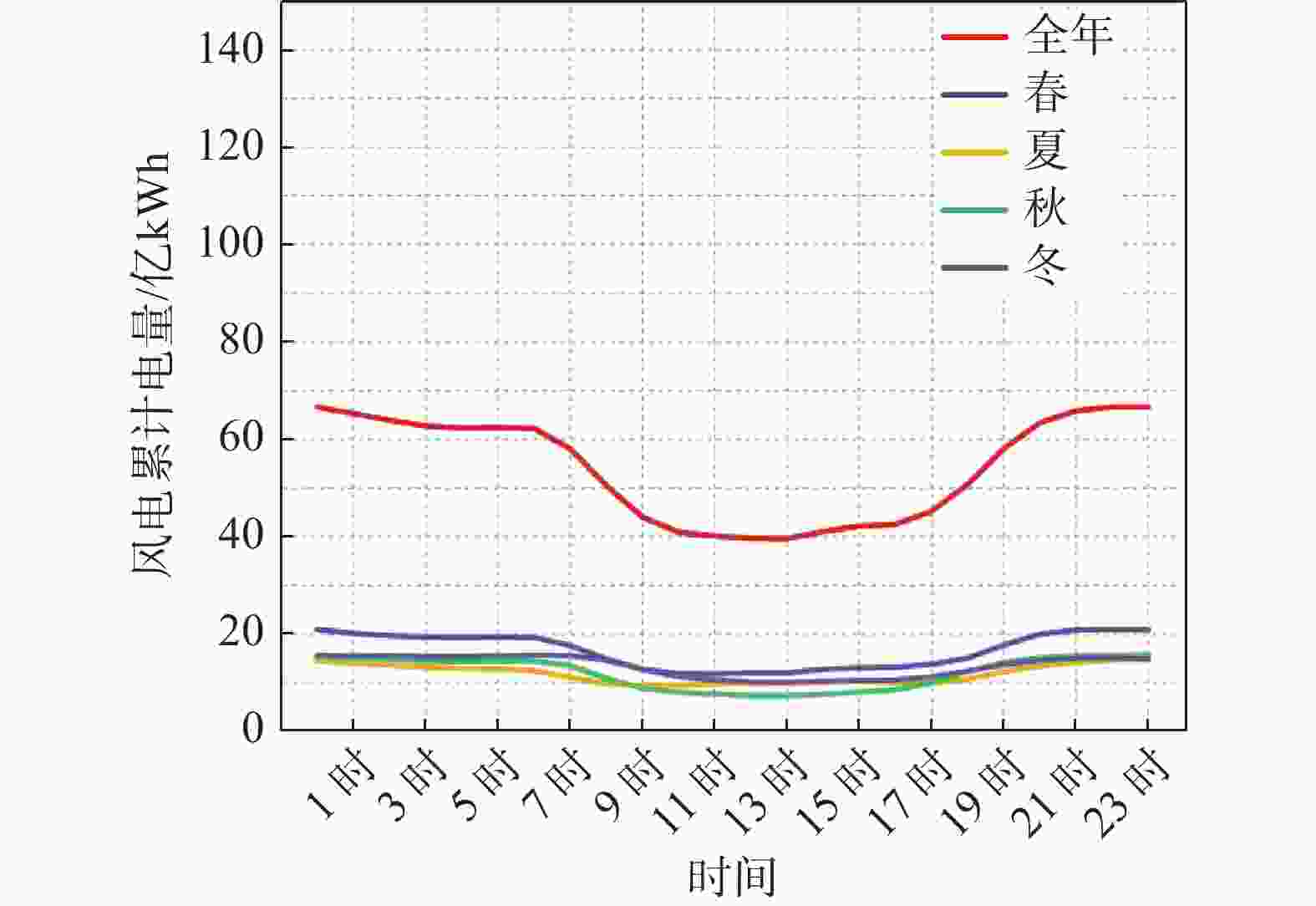
地区新能源电量指标如表3所示,风电和光伏出力系数在[0, 0.62]区间贡献了全年95%的电量;地区新能源电量季特性分布如图4和图5所示,从时段上看,风电在7:00-20:00时累计电量相对较少,在21:00-6:00时累计电量较多,即白天风电电量少,夜晚风电电量多。光伏与风电相反,呈现午间11:00-14:00时大,夜晚无的特性。从季节性上看,四季呈现的特性较为统一,均是春季较其他季节电量略多。
指标/p.u. 风电 光伏 Q95 0.615 0.619 Table 3. New energy power quantity index
-
地区调峰特性指标如表4所示,随着新能源的发展,新能源对电网调峰的影响大概率为负面的,即加重了系统的峰谷差,春季的反调峰影响最大,电网需要配置更多的调节手段,相对来讲,夏季与其他季节相比,调峰需要次数和调节资源相对较少。
调峰指标 全年 春 夏 秋 冬 KNeg −180 −180 −92.63 −130.82 −68.31 P+Neg 19 11 35 13 19 P−Neg 81 89 65 87 81 P0Neg 0 0 0 0 0 Table 4. New energy peak regulation index
% -
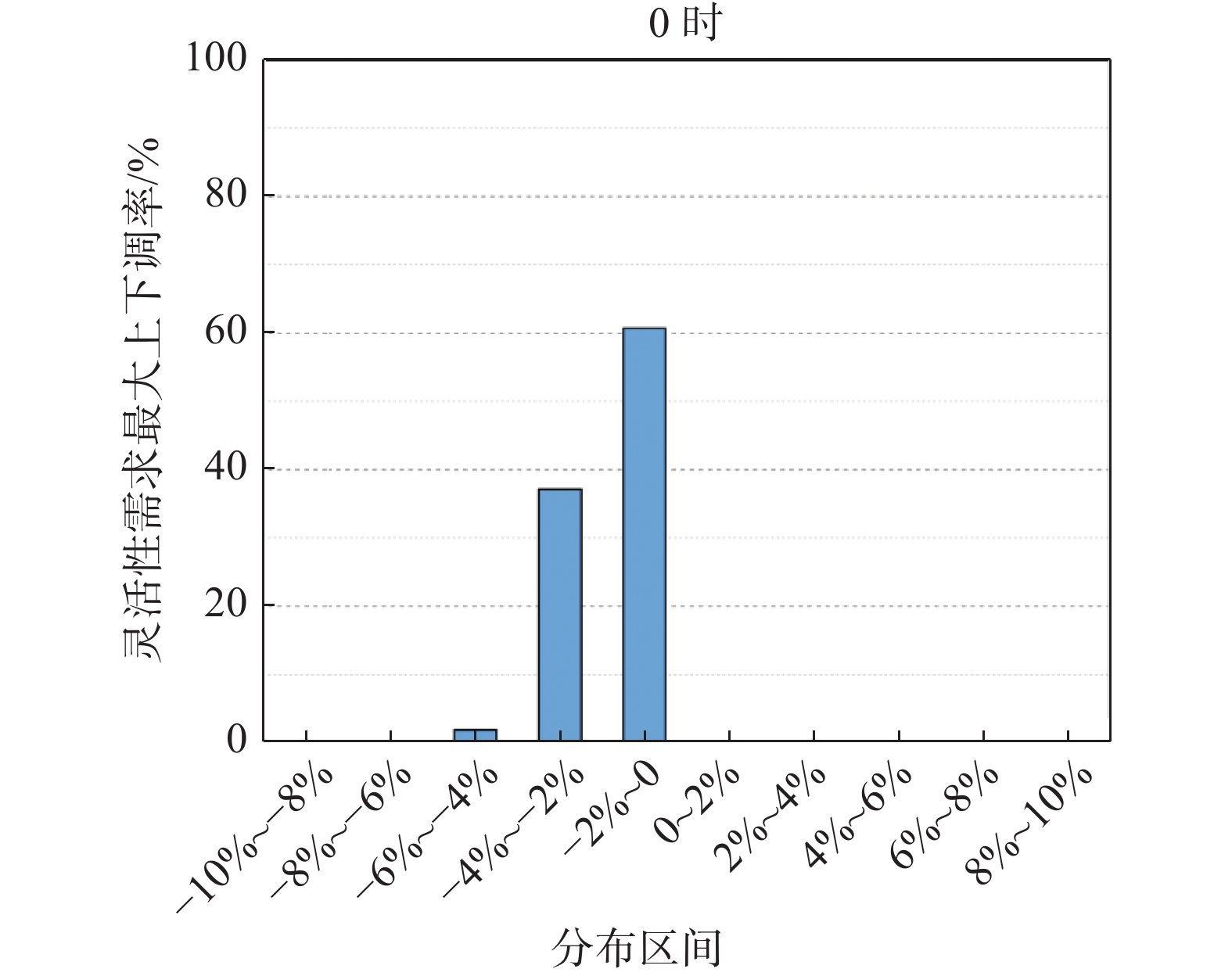
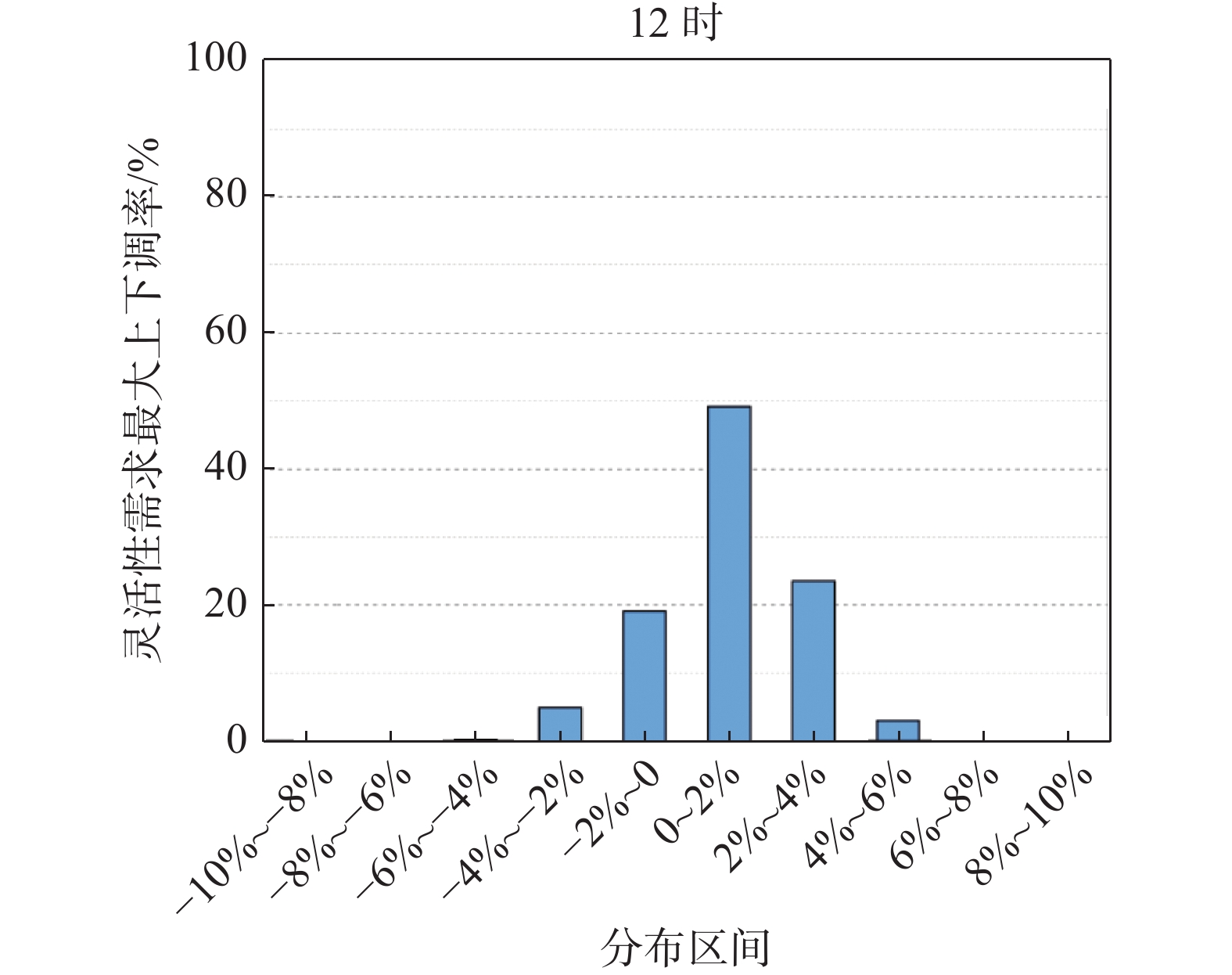
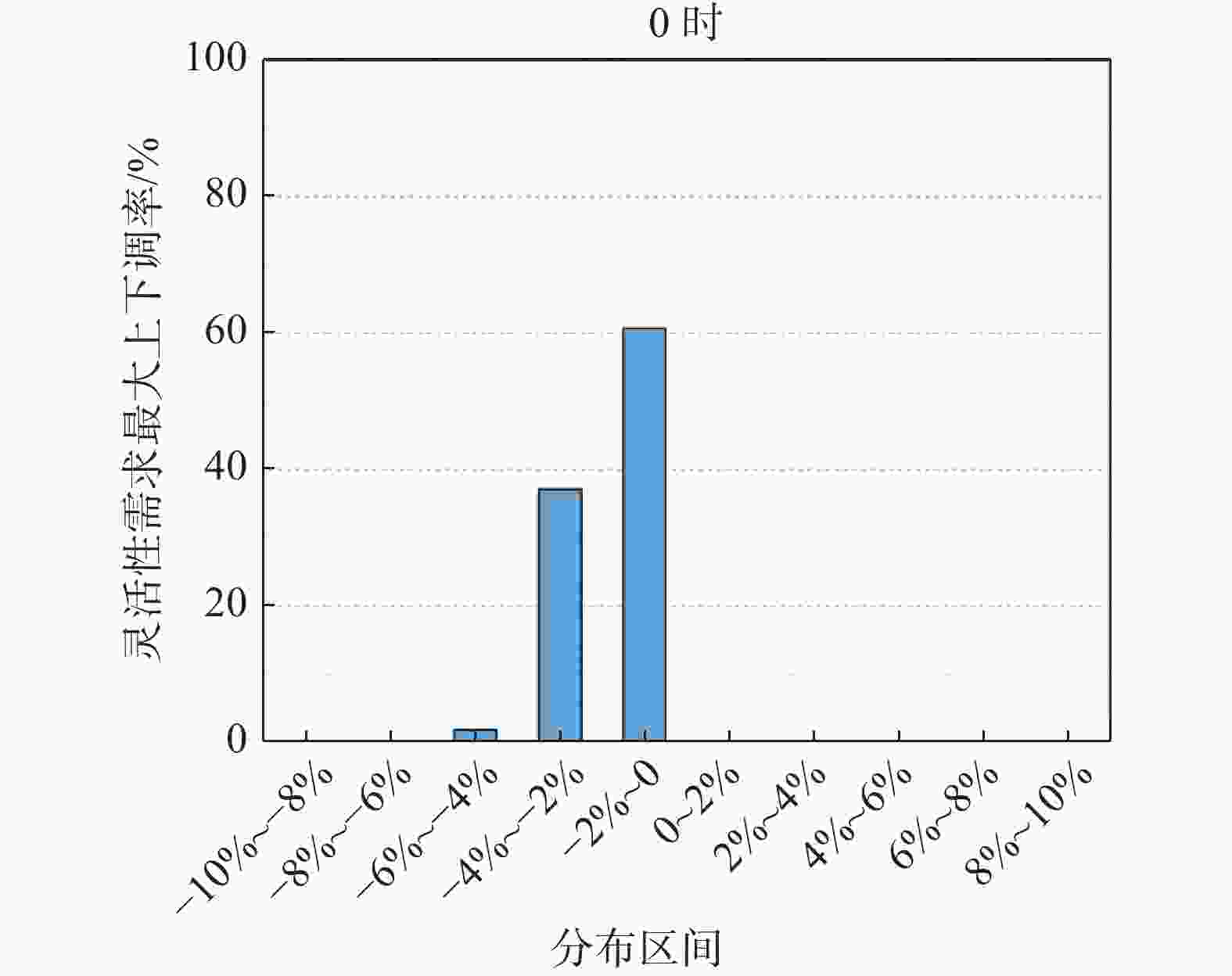
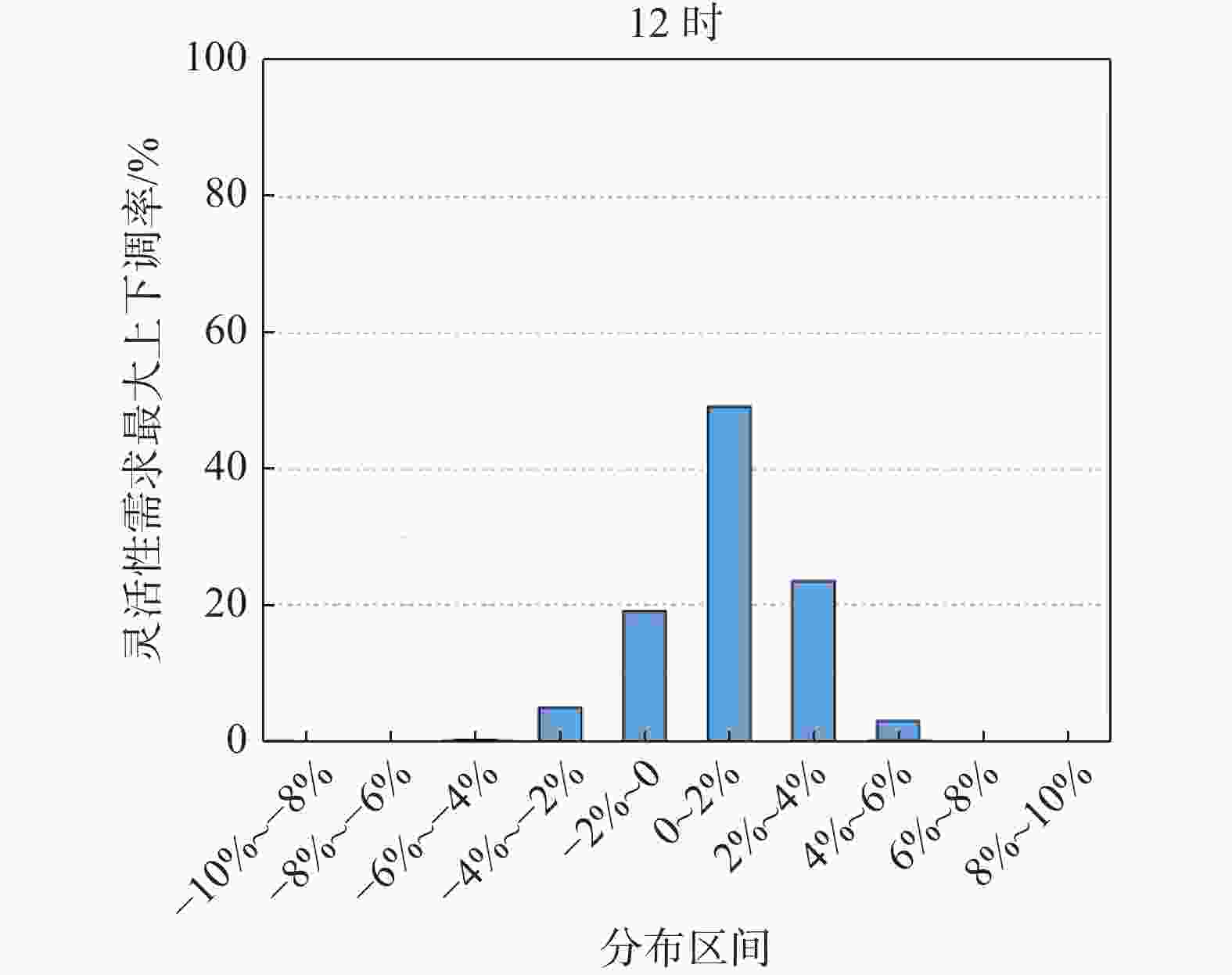
地区灵活性需求指标如表5所示,随着时间尺度的增大,系统的波动范围也随着增大,从年数据上看,向上和向下需求基本对称分布的;就时刻特性如图6和图7所示,1 h尺度下,晚间时段灵活性需求大都分布在−2%~0,午间灵活性需求大都分布在0~2%。
灵活性需求指标 15 min 1 h 4 h R+max 3.3 9.9 25 R−max −3.4 −8.1 −25 Table 5. New energy flexibility demand index
% -
文章从新能源对电网影响的角度,对评估指标进行分析,总结出适用于不同时间尺度评估体系和评估指标,用于反映新能源与电网的交互影响,并应用文章所提方法对某地区以实际运行数据为例计算了典型指标,分析不同尺度下地区的新能源特性对电网的影响,结果表明文章提出的各类指标能够快速量化电网与新能源的相关特征,从而充分挖掘出典型场景的源荷特征,为以新能源为主体的新型电力系统的规划、运行及建模提供参考和评价依据。
Impact Assessment of New Energy Characteristics on Regional Power Grid Considering Multiple Time Scales
doi: 10.16516/j.gedi.issn2095-8676.2023.05.020
- Received Date: 2022-10-27
- Rev Recd Date: 2023-01-11
- Available Online: 2023-08-21
- Publish Date: 2023-09-10
-
Key words:
- wind power /
- photovoltaic power /
- index system /
- peak regulation /
- flexibility /
- data mining
Abstract:
| Citation: | ZHANG Xuemeng, MENG Xiangjuan, MAO Fubin, LI Yuliang, CHEN Fan. Impact Assessment of New Energy Characteristics on Regional Power Grid Considering Multiple Time Scales[J]. SOUTHERN ENERGY CONSTRUCTION, 2023, 10(5): 166-173. doi: 10.16516/j.gedi.issn2095-8676.2023.05.020 |



























 DownLoad:
DownLoad: