Research on Decomposition of Urban Energy-Saving Indicator Based on Combination Weighting and Clustering

能源是实现碳达峰、碳中和不可或缺的关键支撑要素。随着我国能源消费总量的不断提升，以控制单位GDP能耗下降和消费增量为关键的节能工作意义愈发凸显，政府相关的措施力度也不断加强。国家“十一五”规划纲要首次设立单位地区生产总值能耗下降这一约束性指标，明确要求“十一五”末的单位地区生产总值能耗要在五年前的基础上下降20%，这一举措推动了节能工作落到实处，将节能降耗作为政府的一项制度性安排；到“十二五”时期，节能政策进一步完善，在控制单位国内生产总值能耗下降目标的前提下，要求对能源消费总量进行合理控制；“十三五”时期逐步形成相对完整的能耗“双控”政策体系， “十三五”节能减排综合工作方案提出要加强能耗“双控”约束力度，将节能目标逐层分解到下级行政区，让节能指标的地区分解成为了地区上下协同推进完成能耗“双控”任务的主力抓手；在“双碳”目标下，2021年中央提出要创造条件尽早实现能耗“双控”向碳排放总量和强度“双控”转变，标志着在“双碳”目标下，我国节能减排工作即将迎来重要转折。“十四五”时期国家对能耗“双控”制度提出更高的站位要求，近期出台的相关政策中^[1]提出要在能效优先的基础上，保证合理用能，对新增可再生能源和原料用能不纳入能源消费总量控制，突出了能源消费强度指标控制的重要性，并要求进一步完善指标设置及分解落实机制。

在对能耗“双控”指标的定性研究方面，文献[2]等在分析我国单位GDP能耗中指出其优化的关键因素是产业结构调整；文献[3]认为产业结构与能源消费结构优化均可以有效提高能源效率；文献[4]从政策强制性角度研究其对单位生产总值能耗的影响，结果表明以行政执法等手段为主的政策强制性措施对能耗强度具有较明显的控制作用，并且可通过约束能耗强度的下降进一步约束碳排放强度下降。在地方能耗“双控”研究层面，文献[5]以徐州市为例，通过关联分析法分析了高耗能行业与节能降耗的主要影响因素；文献[6]以重庆市为例，分析了碳达峰碳中和目标下影响能耗“双控”目标的主要因素为用能效率和产业结构，并基于主要因素作出了情景假设，给出实现节能降耗的路径。在定量研究节能指标上，文献[7]采用时序分析法挖掘能源消费与地区经济发展的关联关系，分析中国30个省区历年单位生产总值能耗与人均GDP的相关性，并结合经济和能源消费体量等因素，计算出各地区对于全国节能目标的贡献程度。文献[8]建立了数学模型，探讨分析如何将20%的节能指标向下级行政区分解。

主客观组合赋权法从专家先验知识、熵值计算两个维度对个案的多指标进行权重设计，广泛应用于指标体系的综合评价^[9-16]，其中，文献[9]为对核电的节能效果进行评价，从能耗强度、经济效益等方面应用熵权法进行赋权评价；文献[10]和文献[11]均采用层次分析与熵权法评价综合能源系统多指标及配电网指标体系；文献[12]利用客观赋权法对清洁可再生能源的节能潜力进行评估。聚类分析是通过计算样本在多维指标上的相似度来将相似度不高的样本区分开来，文献[13]在省级节能指标分解中采用了系统聚类的方法对各市州差异进行区分；文献[14]在用电需求潜力评估中使用了两阶段聚类分析方法；文献[15]采用聚类分析方法对中国能耗强度的决定性指标进行实证研究。文章以某市“十四五”单位GDP能耗下降强度目标分解为例，参照国家“十四五”能耗双控目标分解原则，选取契合分解原则的几类指标，形成目标分解的评价指标体系，再采用组合赋权与聚类分析结合的方法，构建各区县（市）能耗强度下降指标评价模型并对所选指标体系进行权重计算，得出各区县（市）所在的能耗强度下降档位。测算仿真结果表明该方法符合“十四五”能耗“双控”目标分解原则与要求，具有较为可靠的政策指导性。

根据“十四五”能耗双控指标地区分解“突出强度约束、实行奖惩并重、兼顾地区差异”的原则，综合考虑各地区能源消费总量、GDP、节能潜力、发展阶段与功能定位等因素，选取各地区“十三五”末单位GDP能耗、“十三五”强度下降目标完成情况、“十三五”能耗增量完成情况以及能耗总量占全市的比重4个指标，构建双控指标分解体系，其中能耗总量比重指标包含了各区县可再生能源消费量，在后续研究分析中可通过摸底可再生能源消费量数据对分解结果进行调整修正，确保结果更加合理，符合政策导向，见表1 。

以某市各区县（市）能耗与经济相关数据为例，对以上指标进行计算和梳理，得出强度下降目标分解基础数据见表2。

在对数据进行测算分析时，由于所选指标体系的基础数据量纲各异，部分指标在不同区县上的差别较大，若直接使用原始数据测算会使结果导向有较大差异的指标，从而忽略了其他指标及中间位置区县的差异，对结果产生较大影响。为保证结果准确无偏差，需对其进行规范化处理。考虑区县个数为9个，现将各指标数据进行排序并分列5档，根据排序情况对各区县（市）指标进行赋分1～5分。得出结果如表3所示：

经预处理后，增量目标完成情况指标无明显差异，结合各区县（市）“十三五”实际增量使用情况，除E县增量指标稍有剩余，其余地区使用率均接近100%，该指标不具备区分地区差异的条件，故不予考虑。

将主、客观赋权方法相结合的组合赋权法融合了两类方法的优点，使指标评价及分解结果更为精确和科学。根据既有指标体系构建基于组合赋权的指标分解模型如下：

式中：

${Y_i}$ ——$i$地区的综合得分；

${x_{ij}}$ ——$i$地区在$j$指标上的数值；

${\alpha _j}$ ——组合权重，由主观权重与客观权重共同构成，表达式为：

${w_j}$，$w_j^{'}$分别为主观权重和客观权重，$a$与$b$分别为两类权重对应的权重系数，该系数表示了两类权重的重要性，二者一同构成组合权重。

层次分析法是一类兼具定性分析和定量分析的主观赋权方法，可将定性问题进行定量化处理。多应用于多目标系统综合评价与权值分配问题。

1）构造参考因素比例标度表

比例标度表是通过比值对因素对之间的重要程度进行衡量的方法。典型的比例标度表如表4所示：

2）形成节能指标分解的判断矩阵

参考比例标度表，根据政府主管部门对相关指标的经验判断，在不影响最终主观赋权结果的情况下，考虑不同专家对三类指标的重要性程度排序的量化赋值有所不同，综合选用1,3,5三类标度量化值对指标进行两两之间重要性衡量，构造出判断矩阵见表5：

3）计算权向量

a.计算元素累积：

b.计算${m_i}$的$n$次方根$\overline {{w_i}} $，即几何平均数：

c.对向量${{\boldsymbol{w}}_{\rm{s}}} = [{w_{{\rm{s}}1}},{w_{{\rm{s}}2}}, \cdots ,{w_{{\rm{s}}n}}]$归一化，得出权重系数${w_{{\rm{s}}i}}$：

则${W_{\rm{s}}} = {[{w_{{\rm{s}}1}},{w_{{\rm{s}}2}}, \ldots ,{w_{{\rm{s}}n}}]^T}$为指标体系的权向量。

4）层次分析法一致性检验

a.计算最大特征根${\lambda _{\max }}$；

b.计算一致性指标$C_{\rm{R}}$：

$R_{\rm{I}}$是算法中的平均随机一致性指标，通过查表，可根据不同的评价指标个数得出该指标的对应值见表6：

当$C_{\rm{R}} < 0.1$时，表明判断矩阵一致性检验有效，否则表明当前判断矩阵不具备满意的一致性。

基于能耗双控指标组成的判断矩阵，运用层次分析法计算出各类指标的主观权向量${W_{\rm{s}}} = [0.47,0.16,0.37]$，根据公式（7）算得$C_{\rm{I}} = 0.02$，由$n = 3$可查得随机一致性指标$R_{\rm{I}} = 0.58$，算出检验系数$C_{\rm{R}} = 0.034 < 0.1$,满足一致性约束，至此便确定了评价指标体系的主观权重。

以熵值法为代表的客观赋权法可以通过计算信息熵来判定指标间的相似程度，进而反映选取指标体系对评价结果的重要性，与以层次分析法为代表主观赋权法形成互补。

1）指标预处理

通过标准化处理各指标：

式中：

${x_i}$ ——第$i$项指标的原始值；

$x_i^{'}$ ——第$i$项指标的标准化值；

${x_{i\max }}$——$i$项指标的最大值；

${x_{i\min }}$——$i$项指标的最小值。

2）指标的熵权值计算

a.计算第$j$项指标下第$i$个地区的指标比例：

b.计算第$j$项指标的信息熵：

c.计算第$j$项指标的权重：

$m$为地区数，$n$为指标数，${W_{\rm{o}}} = {[{w_{{\rm{o}}1}},{w_{{\rm{o}}2}}, \ldots \ldots ,{w_{{\rm{o}}n}}]^T}$即为所求客观权重向量。

基于能耗双控指标数据，构造原始数据矩阵，通过预处理、计算信息熵等过程，得出各类指标的客观权重见表7。

选定适当的主客观权重系数，结合公式（2）得到组合权重见表8。

以某市各区县（市）基础数据为例，结合层次分析法与客观赋权法得出的权重，代入分配模型中，得出各区县（市）在能耗、经济方面的综合评价结果，数值越低表明其能效水平越高。根据表9结果，各地区在能耗强度、“十三五”能耗双控目标完成情况及能耗总量等指标情况上均有不同侧重，其中C县排位相对靠前，能耗强度下降压力较小；B县、D县、E县得分较一致，属于中等能耗强度水平地区，A县、H县、G县及I县的排位靠后，能耗强度下降形势相对严峻。

聚类分析依据多个指标对个案进行相似度计算并归类分档，能有效降低统计分析中的信息损失，区分各地区能耗强度下降档次。根据所选指标体系与组合赋权的得分结果，基于SPSS分析软件，采用Ward系统聚类法对地区能耗强度下降目标档次进行聚类，得出聚类系谱图，以进一步验证组合赋权的准确性，得出较为直观的可视化结果如图1所示。

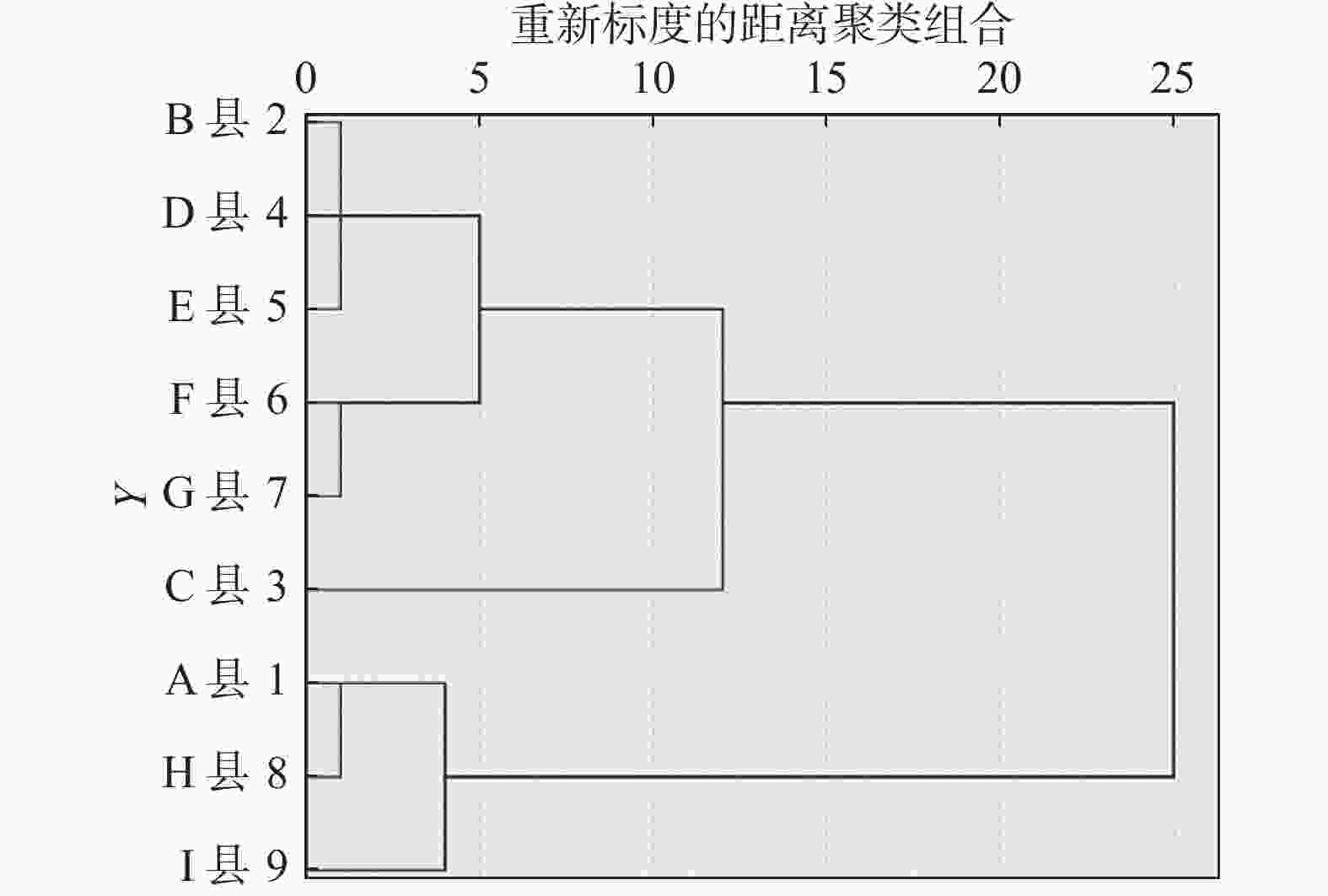
Figure 1.  Target cluster family tree of energy consumption intensity reduction in each district/county (city)

当迭代次数达到5时，B县、D县、E县聚为一类，对应组合赋权综合得分在2分的区段；F县、G县为一类，对应3分段；C县自成一类，对应1分区段；A县、H县、I县聚成一类，对应得分在3.5分以上，聚类结果与组合赋权基本一致。

根据国家、省“十四五”能耗双控工作的有关要求与目标分解原则，基于某市“十四五”单位GDP能耗下降14.5%的基础目标与15%的激励目标，在确保全市单位GDP能耗下降达激励目标且GDP增速负荷预期的前提下，结合赋权与聚类分析的结果，兼顾各区县（市）发展实际与功能定位，对全市9个区县（市）设定14.5%、15%、15.5%三档次强度下降激励目标，以保证能源消费增量目标可免予上级考核。

根据表9中各区县（市）组合赋权得分和图1聚类系谱图结果，得出某市“十四五”分区县（市）能耗强度下降目标分解结果（表10），能效水平较高的B县、C县、D县、E县其节能压力较小，下降目标划分在14.5%档；F县、G县评分相对靠后，节能压力适中，强度下降划分在15%档；H县、I县评分垫底，节能增效压力较大，划分在15.5%档；需要特别说明的是，A县2020年二产GDP占比仅为12%，三产GDP比重高达87%，根据兼顾地区差异的分解原则，可适当采取人为修正的手段对划分结果进行调整，以得出符合地区实际的分配结果。结合A县实际，综合考虑对其设定14.5%的单位GDP能耗下降目标。综上，得出的分解结果符合政府能耗强度下降目标管理要求。

能耗双控制度是我国践行生态文明理念、促进高质量发展的政策保障，也是实现“双碳”目标的重要制度安排，推动能耗双控目标层层分解落实到各地区是压实地方责任、坚持上下一盘棋实现节能降耗的重要抓手。本文聚焦典型城市单位GDP能耗下降分区县（市）目标分解，从能源消费、经济发展、节能潜力等方面选取单位GDP能耗、能耗总量、“十三五”强度下降目标完成情况等指标建立对各区县（市）的节能水平进行评价的指标体系，通过层次分析与熵值法得出各指标体系的组合权重，结合聚类分析方法，得出客观、可靠且符合实际的分区县（市）能耗强度下降目标分解结果，为政府部门制定节能有关的政策措施提供了经验参考和理论依据。同时，加强碳排放总量和强度“双控”制度建设是实现“双碳”目标的必要前提^[17-21]，而用好能耗双控制度，则有利于进一步推动能耗“双控”向碳排放 “双控”的转变，更加凸显以降碳为核心的节能减排工作，兼顾发展和降碳，助力实现碳达峰碳中和目标。