Research on Factors Influencing the Heat Dissipation Performance of Semi-Direct Drive Permanent Magnet Wind Generator

风电行业技术飞速发展，风力发电机组容量不断提升，发电机发热功率也随之增加，这对发电机散热性能要求提出了更大的挑战^[1-3]。发电机运行时若无法及时将热量散出，将导致发电机超温从而引发一系列问题，如永磁体退磁、电路绝缘层破损、降低器件寿命甚至设备损毁^[4-5]。近年来，发电机散热问题日益突出，散热系统的研究已经成为学术界和工程界研究的热点^[6-8]。发电机散热系统设计中，风冷散热和水冷散热是两种常用的冷却方式。风冷散热是指通过风扇或泵驱动冷空气流动，实现发电机内部的热传导、热对流从而冷却发电机的方式；水冷散热是指通过冷却水管中的冷却液与发电机内部结构进行能量交换从而实现发电机冷却的方式。由于水冷散热中冷媒热容大、导热系数高，通常用于大功率发电机散热^[9-11]。因此，风冷、水冷系统冷却效率的优化是提升发电机散热性能的关键。

目前，发电机散热分析的方法主要包括等效热网络法、实验测试以及数值计算3种^[12-13]。魏雪环等^[14]采用有限元软件计算了永磁同步电机温度分布，并将结果与热网络法计算结果进行对比。成丹凤^[15]搭建了1∶1的风力发电机实验台，在不同负载条件下开展实验，分析了发电机关键部位的温升情况。施宁强等^[16]采用计算流体动力学的方法分析了直驱式永磁同步发电机温度分布规律及冷却流体流动特性，为发电机设计提供参考。意大利学者Marco Tosett^[17]采用计算流体动力学（CFD）方法，建立缩尺后的发电机模型，计算了发电机内部三维流场和温度场，并分析了各部件温度分布规律。

以上研究主要局限于对发电机内部温度分布进行研究，而关于发电机冷却系统冷却效果影响因素以及冷却系统优化方面的研究还比较缺乏。本文以1台3 MW冷却方式为空-水冷结合、结构完整且可直接用于整机组装的大功率半直驱永磁同步发电机为基础，采用CFD的方法对半直驱永磁同步风力发电机三维温度场进行分析，探究额定功率条件下发电机温度分布规律以及冷却系统散热效果的影响因素，并对冷却系统散热性能的优化提出了解决方案。

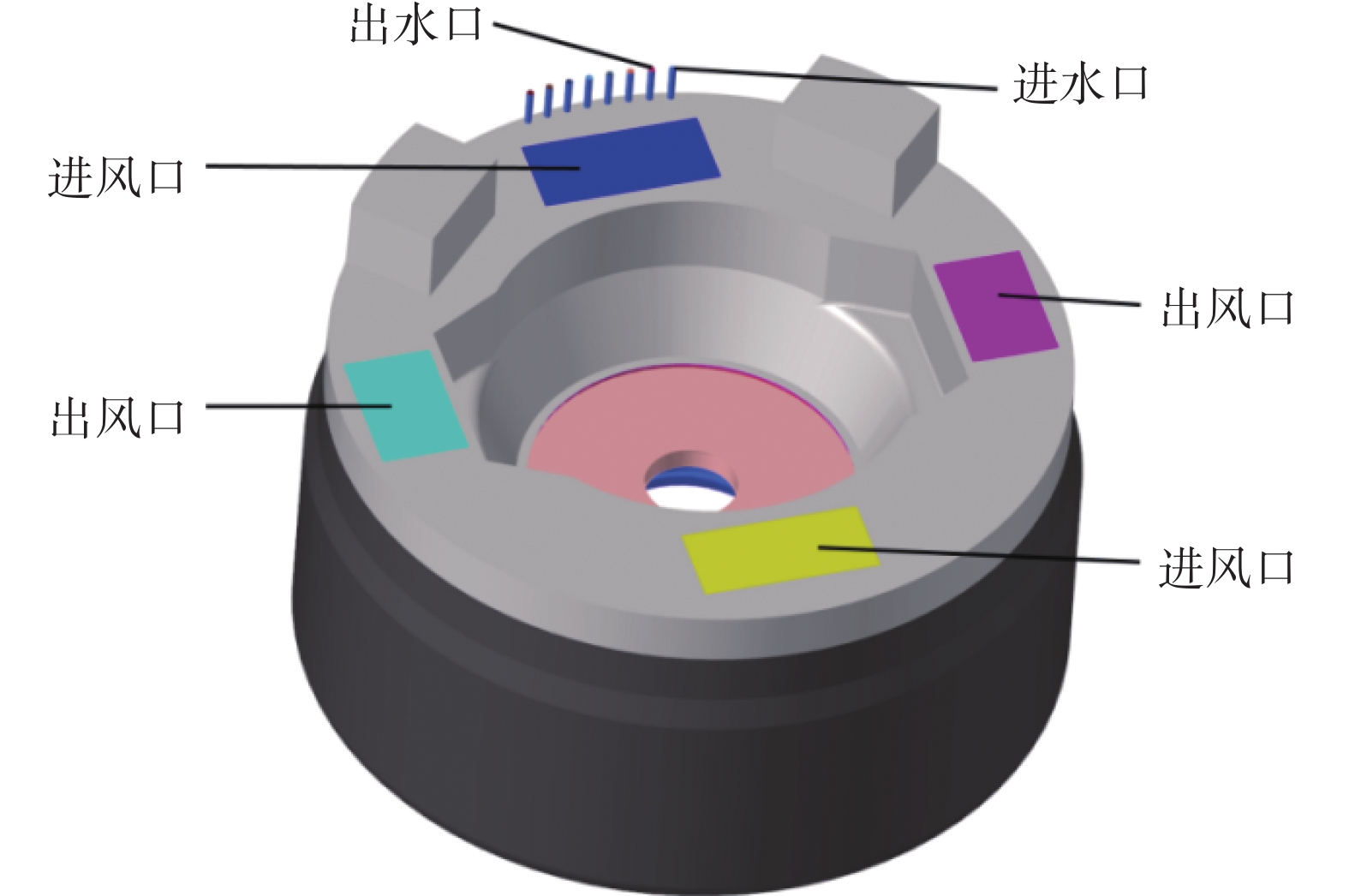
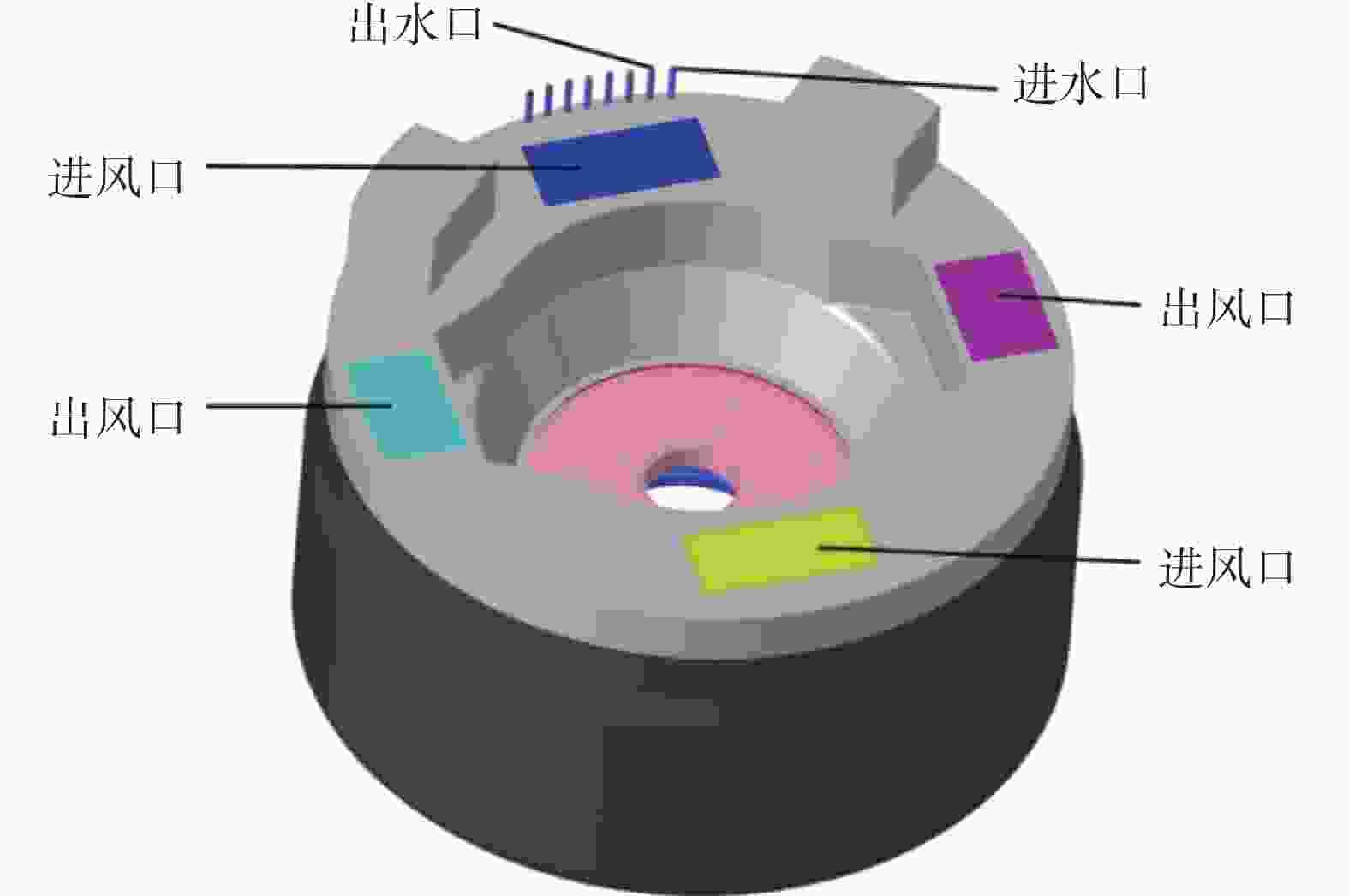
3 MW半直驱永磁风力发电机，发电机耐温绝缘等级按H级（180 ℃）设计，按F级（155 ℃）考核、运行，允许温升100 K。采用风冷系统和水冷系统结合的方式进行散热。风冷系统是在发电机后端盖上开孔并安装散热器进行风冷散热，冷风由进风口被吸入发电机内，与各热源充分换热后由出风口排出，实现发电机的风冷散热功能。水冷系统以安装蛇形冷却水管贯穿定子铁芯的方式对发电机进行水冷散热，进水口和出水口间隔排列，冷水由进水口流入管道内，与内热源充分换热后水温上升，最终由出水口排出。

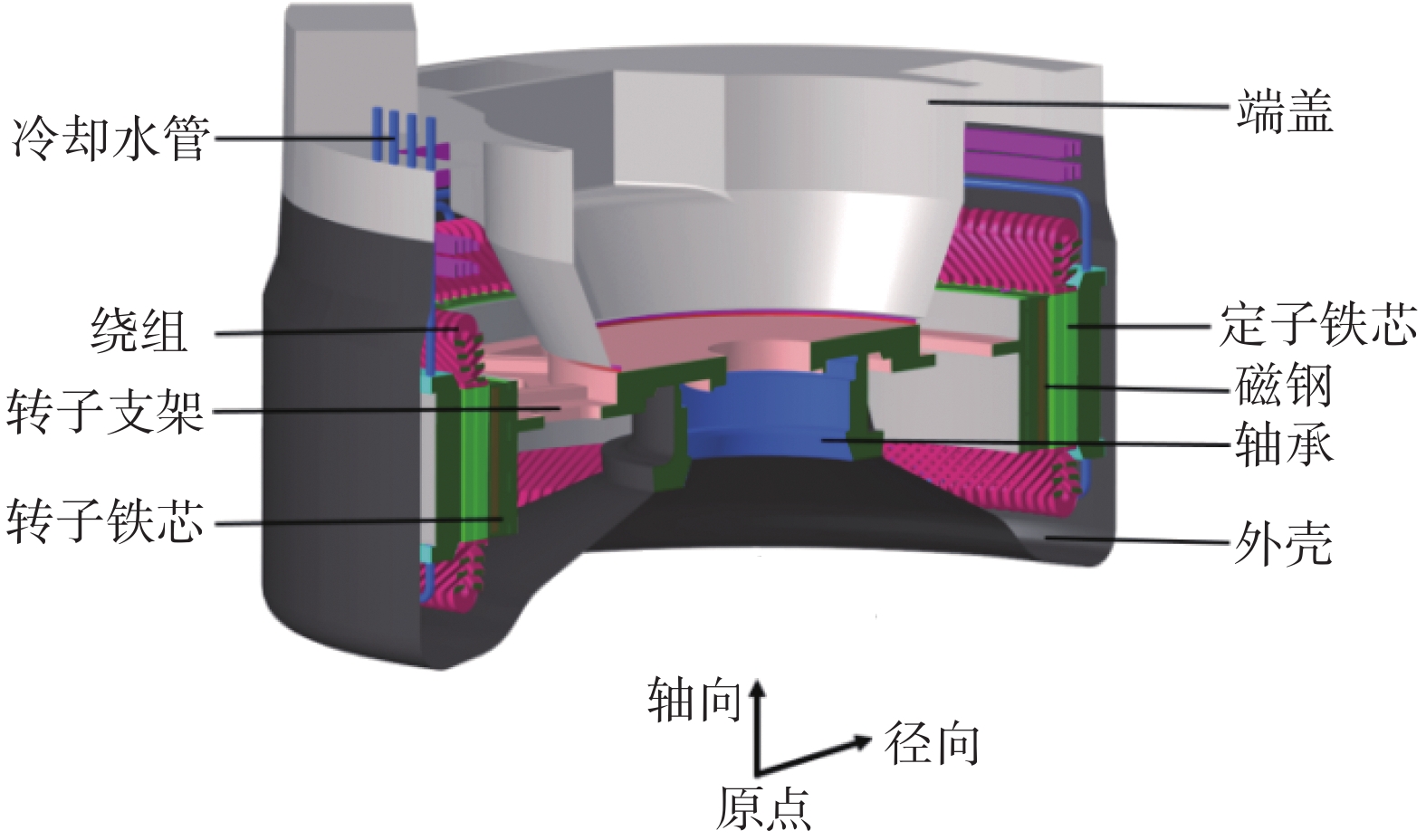
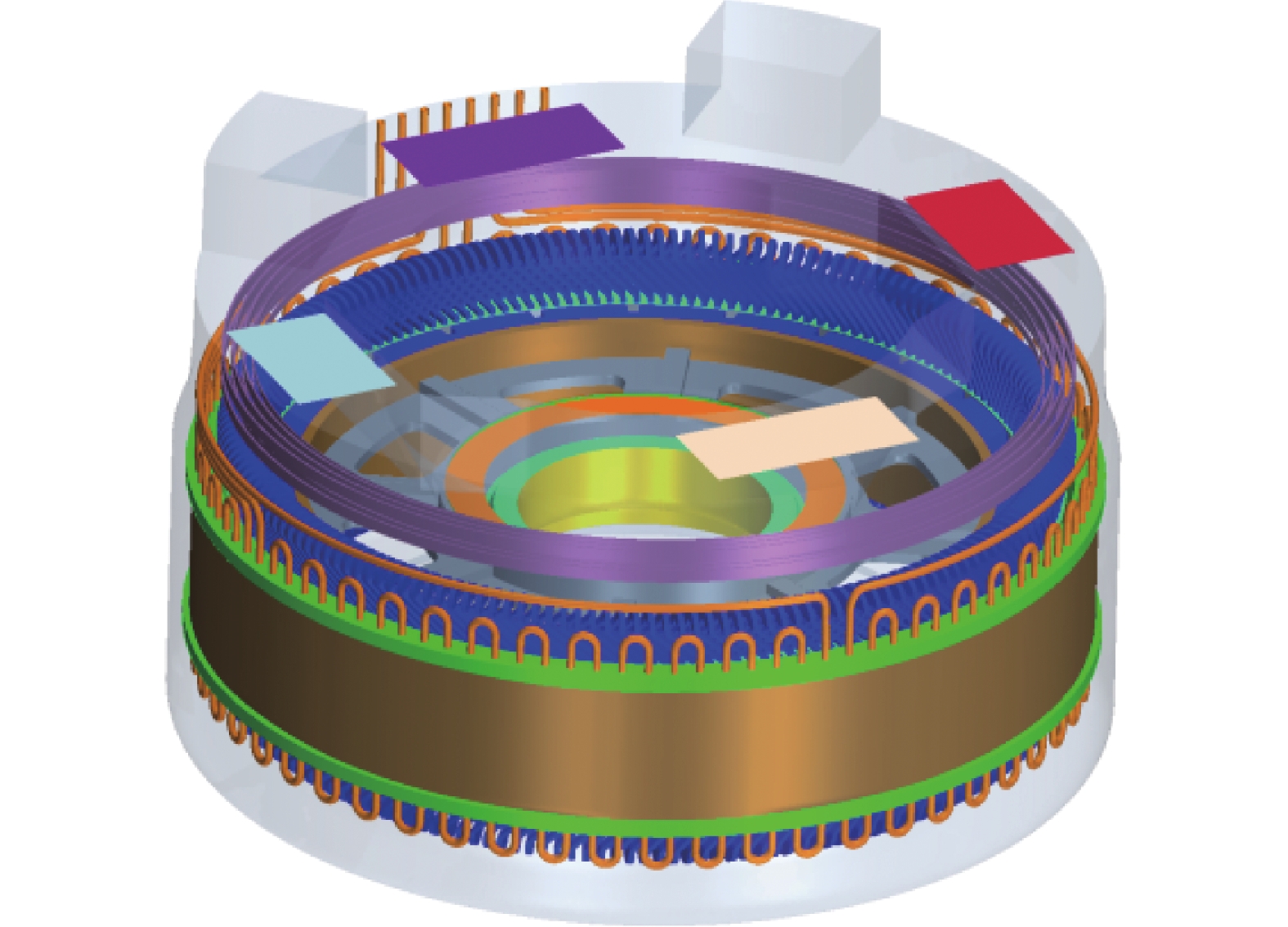
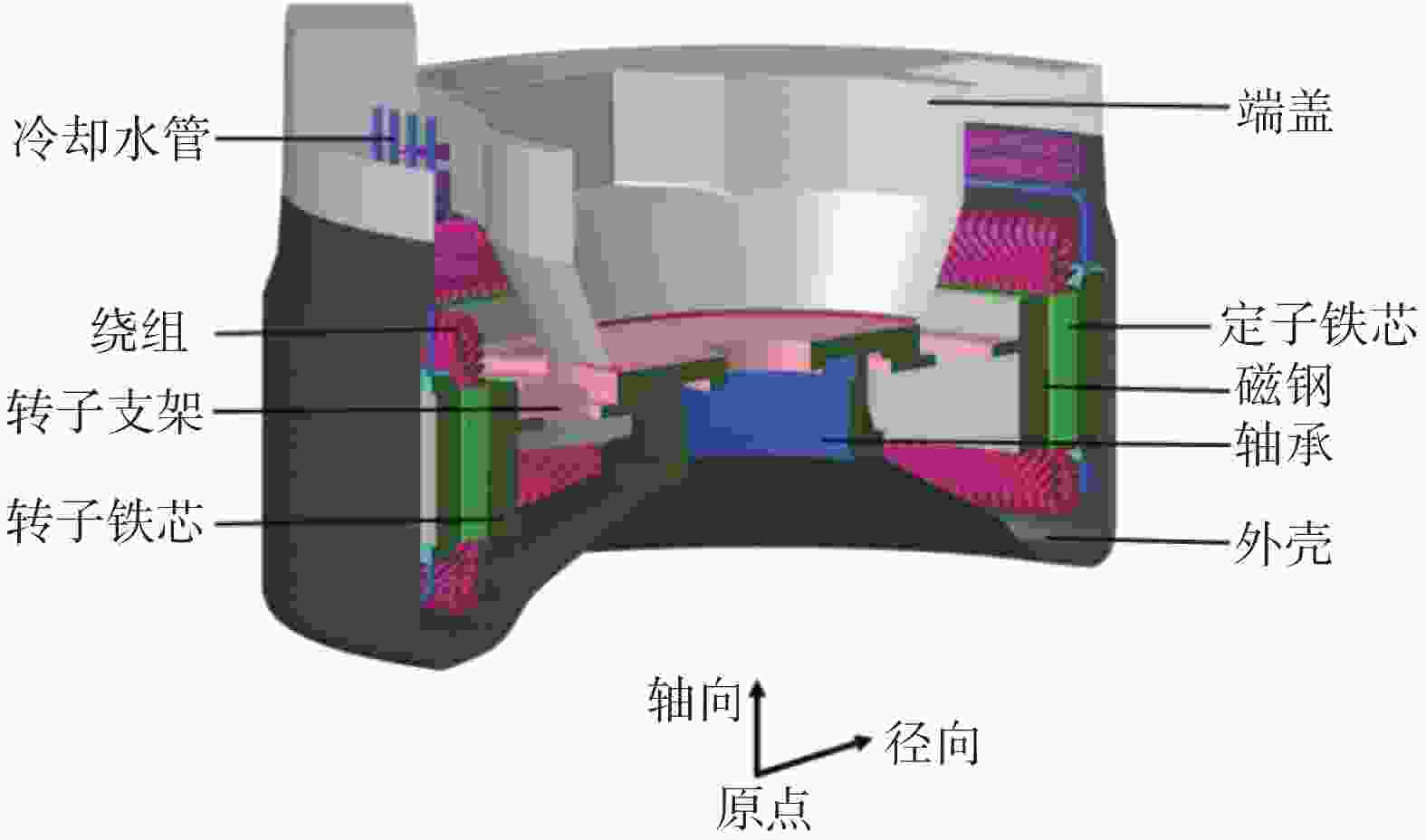
发电机主体主要由定子总成、转子总成、轴承、机壳等结构组成，整体结构如图1、图2所示。发电机坐标轴原点位于外壳底面圆心处，平行于发电机旋转轴的方向为轴向，由外壳底部指向端盖方向为正，垂直于轴向的方向为径向，由旋转轴指向外部为正。

Figure 1.  Structure drawing of the generator air cooling and water cooling systems

Figure 2.  Schematic diagram of the generator structure

本文基于STAR-CCM+软件搭建了发电机散热-冷却一体化三维流动和传热数值模型，物理模型、基本假设和相关参数设置如下。

发电机内流体运动和传热规律满足质量守恒、动量守恒和能量守恒三大定律。

质量守恒方程：

式中：

$\rho $ ——流体密度（kg/m³）；

$t$ ——时间（s）；

$ u $ ——速度矢量（m/s）。

动量守恒方程：

式中：

$P$ ——作用在流体微元上的压力（Pa）；

$\mu $ ——动力粘度（Pa·s）；

${S_{\rm{u}}}$、${S_{\rm{v}}}$、${S_{\rm{w}}}$ ——动量方程的广义源项（N/m³）。

能量守恒方程：

式中：

$h$ ——流体的传热系数（W·（m²·K）⁻¹）；

${c_{\rm{p}}}$ ——比热容（J·（kg·K）⁻¹）；

$T$ ——温度（K）；

${s_{\rm{t}}}$ ——流体的内热源（W/m³）。

实际运行工况下的发电机三维流场、温度场非常复杂，完全还原真实情况的数值计算非常困难。因此，为了提高仿真可行性并保证计算精度，计算过程做出了以下假设^[18-20]：

1）假设发电机各部件材料均匀。

2）绕组中的导线包裹绝缘层，假设绕组具有各向异性导热系数，铁芯由硅钢片叠加而成，硅钢片之间存在绝缘涂层，假设铁芯导热系数为各向异性。

3）假设冷却水均匀、恒温、恒速度流入冷却水管内。

4）忽略重力对空气的影响。

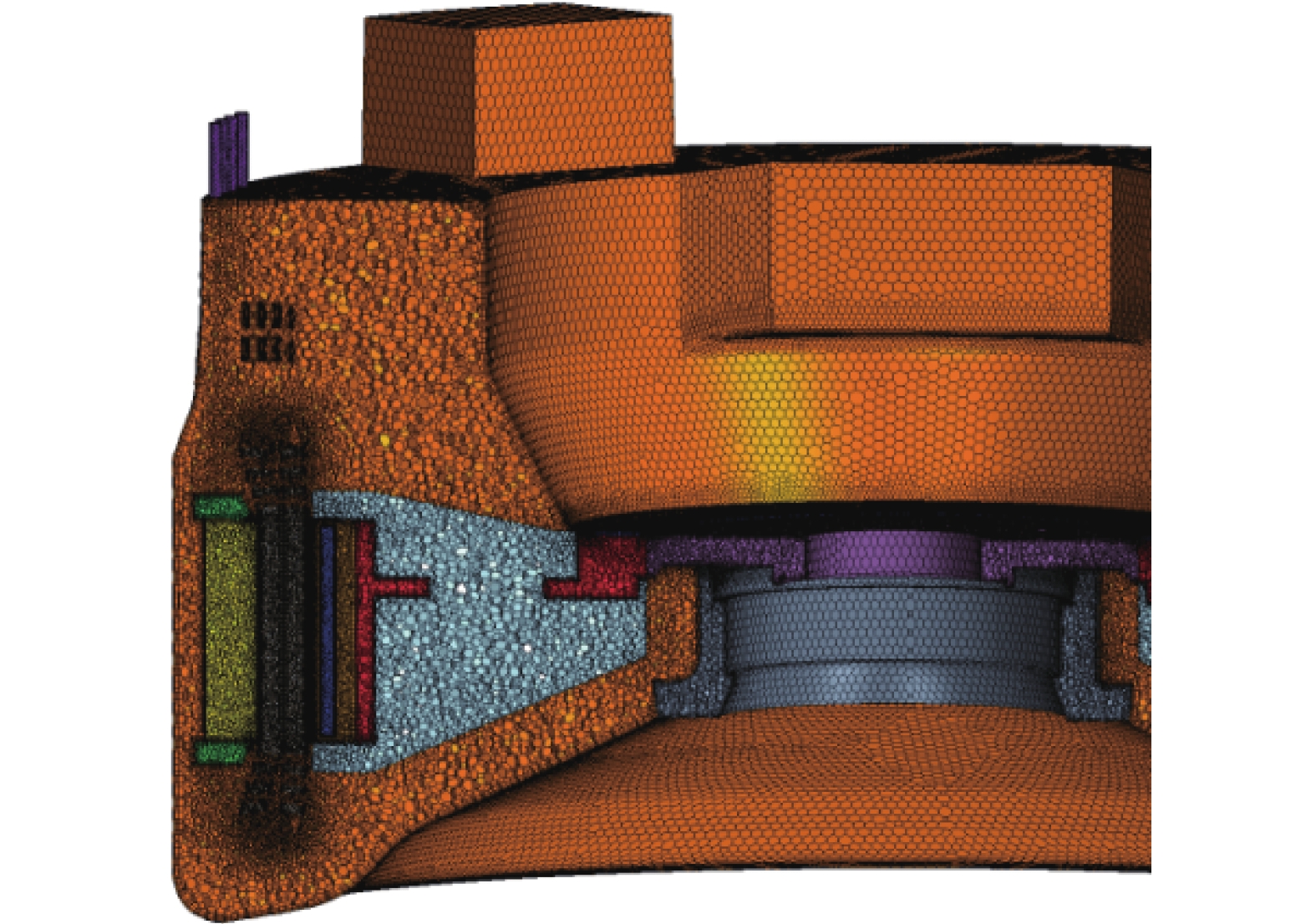
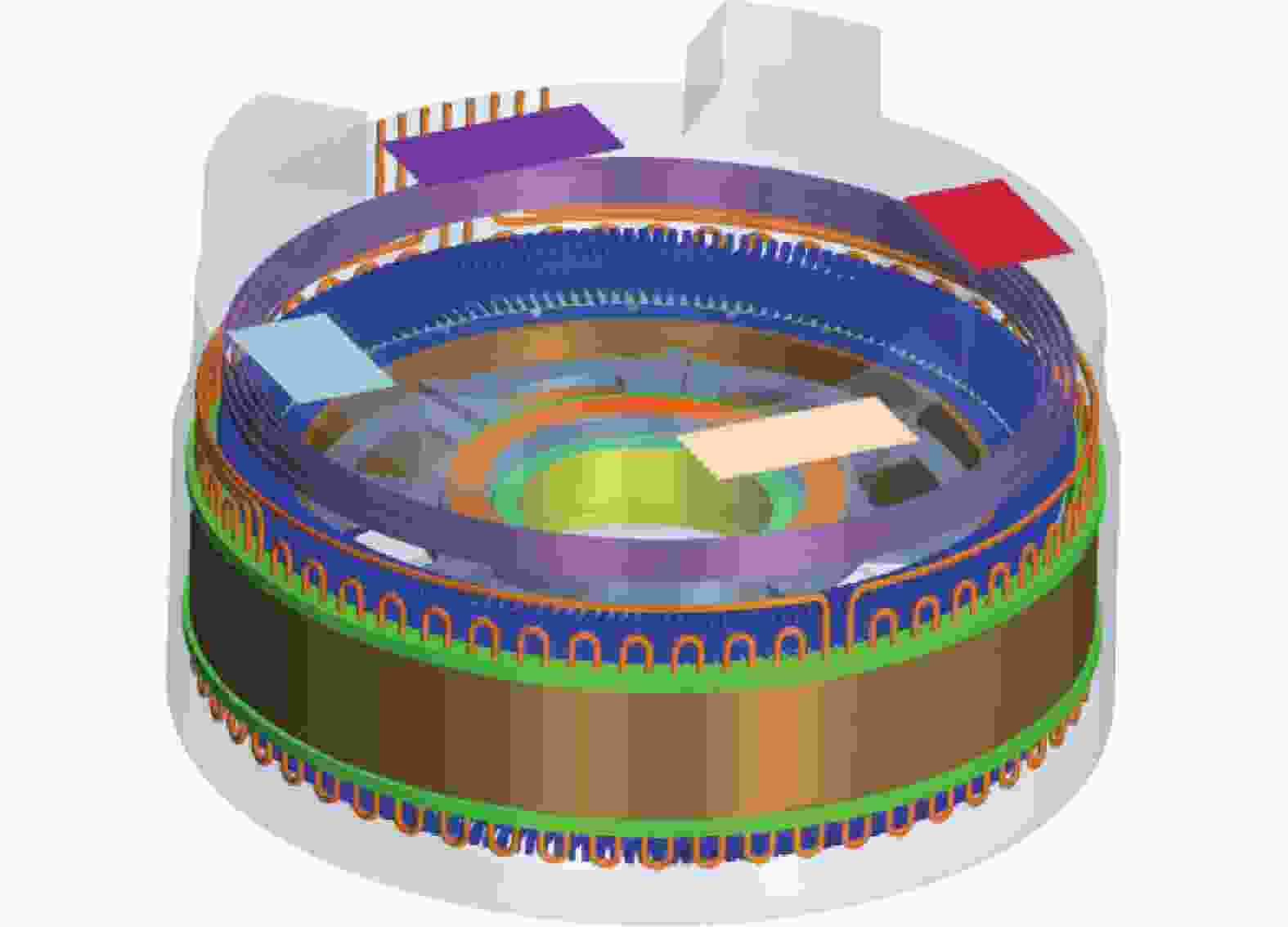
综合考虑计算效率和计算精度，对发电机结构进行了简化处理，忽略螺栓、螺母、铆钉等对流场或温度场影响较小的结构，将多根导线绕扎成的绕组、多层硅钢片压制成的铁芯等效为材料均匀的整体，最终的简化模型应与原模型尽可能保持一致。采用非结构多面体网格对计算域进行离散，由于发电机气隙狭小，因此对该区域附近进行网格加密处理，以准确捕捉气隙内的流动传热。计算模型及网格划分方式如图3、图4所示。

Figure 3.  Simplified model of the generator

Figure 4.  Schematic diagram of the generator grid

为保证计算结果的准确性并尽可能减少计算消耗的资源，共设计了3种网格方案，网格总量分别为1.2×10⁷、1.8×10⁷、2.4×10⁷，以不同监测点的温度变化为参考，在此基础上开展网格无关性验证工作，验证结果如表1所示。由表知，当网格总量达到1.8×10⁷时，计算结果基本保持稳定，此时网格已满足计算需求。因此，本文选择方案2进行网格划分以开展进一步的研究工作。

采用二阶迎风格式对有限体积方程进行离散，时间离散格式为隐式，湍流模型采用${\rm{Realizable}}$${\rm{k}} - \varepsilon $模型。当残差值均小于0.001并且计算域内各物理量数值保持稳定后，视为计算收敛。

本文数值模型边界条件设置如下，风冷和水冷系统中，进水口、进风口的速度由冷媒总进流量确定，边界条件设置为速度入口，出水口、出风口设置为压力出口。本文仿真是以发电机温升实验为参考，实验测试时室内环境温度为31℃，故数值模拟外环境温度也设置为31℃，实验时发电机置于开放环境中，因此四周边界设置为压力出口，压力为一倍的标准大气压。发电机内发热体设置为功率热源。

为验证上述建模方法的可行性以及计算结果的正确性，实验过程中，在发电机绕组、冷却水管出水口、风冷系统出风口不同位置共安装了12个温度传感器，即测点1~12，其中测点1~10布置于不同位置绕组表面，测点11、12分别布置于出水口和出风口处。实时监测额定功率工况和96%额定功率工况的发电机温升情况，实验测试平台如图5所示。

Figure 5.  Experimental test platform

将数值模拟结果与实验结果对比，如表2、表3所示。结果表明，数值模拟结果与实验结果吻合较好，最小误差值为0.2℃，误差比例为0.2%，最大误差值为5.5℃，误差比例为5.1%，误差均在工程误差要求范围内，满足计算精度要求^[16]，说明本文数值模拟的方法准确可靠。

额定工况为机组满发状态，发电功率达到最大值，此时发电机内部各热源发热量达到最大值，是发电机工作的极限状态，也是工程关注的重点工况。永磁风力发电机工作中的主要发热部件为定子绕组和定子铁芯。因此，本文主要对额定工况下永磁同步发电机的定子和绕组进行温度特性分析。

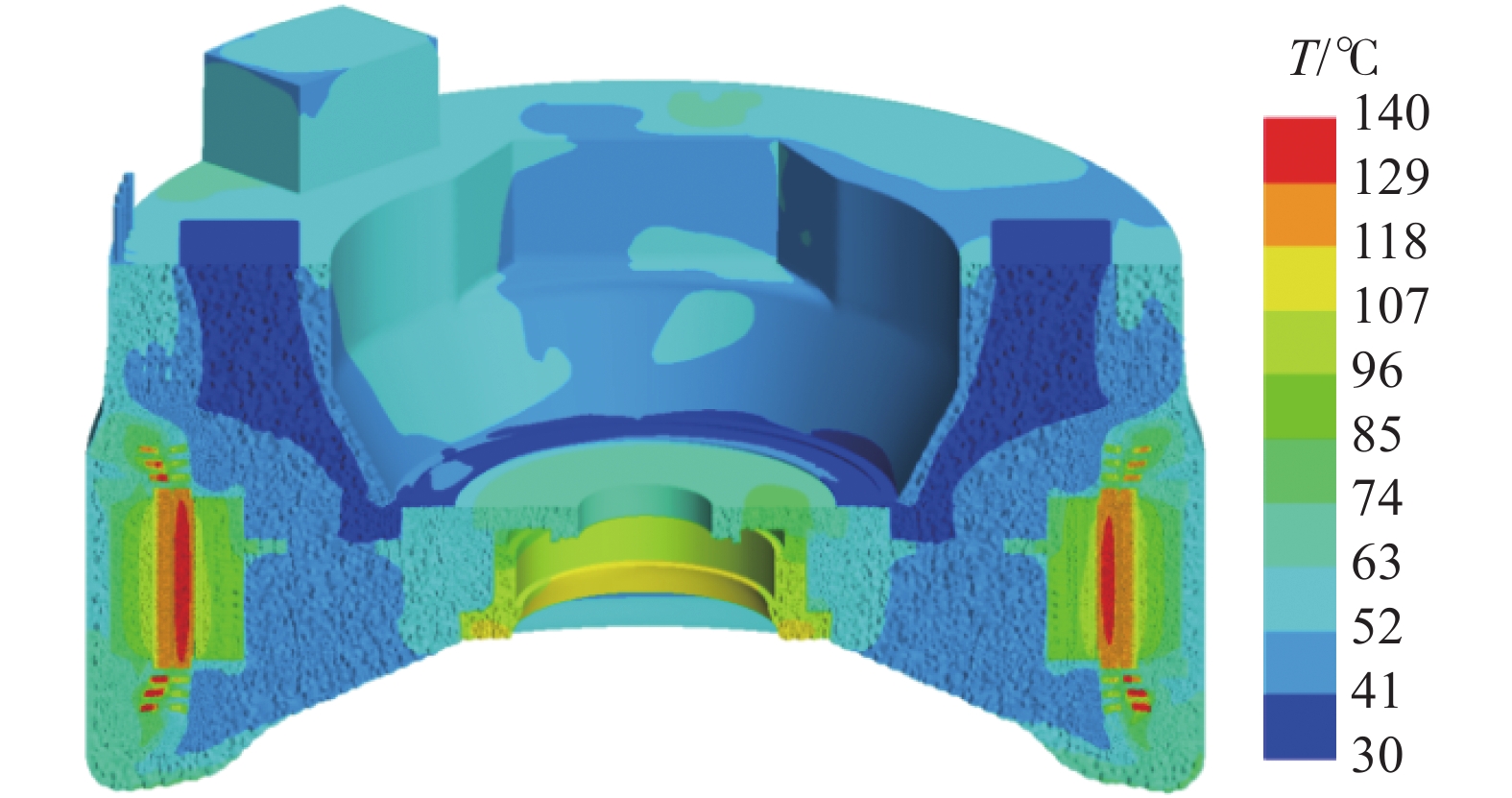
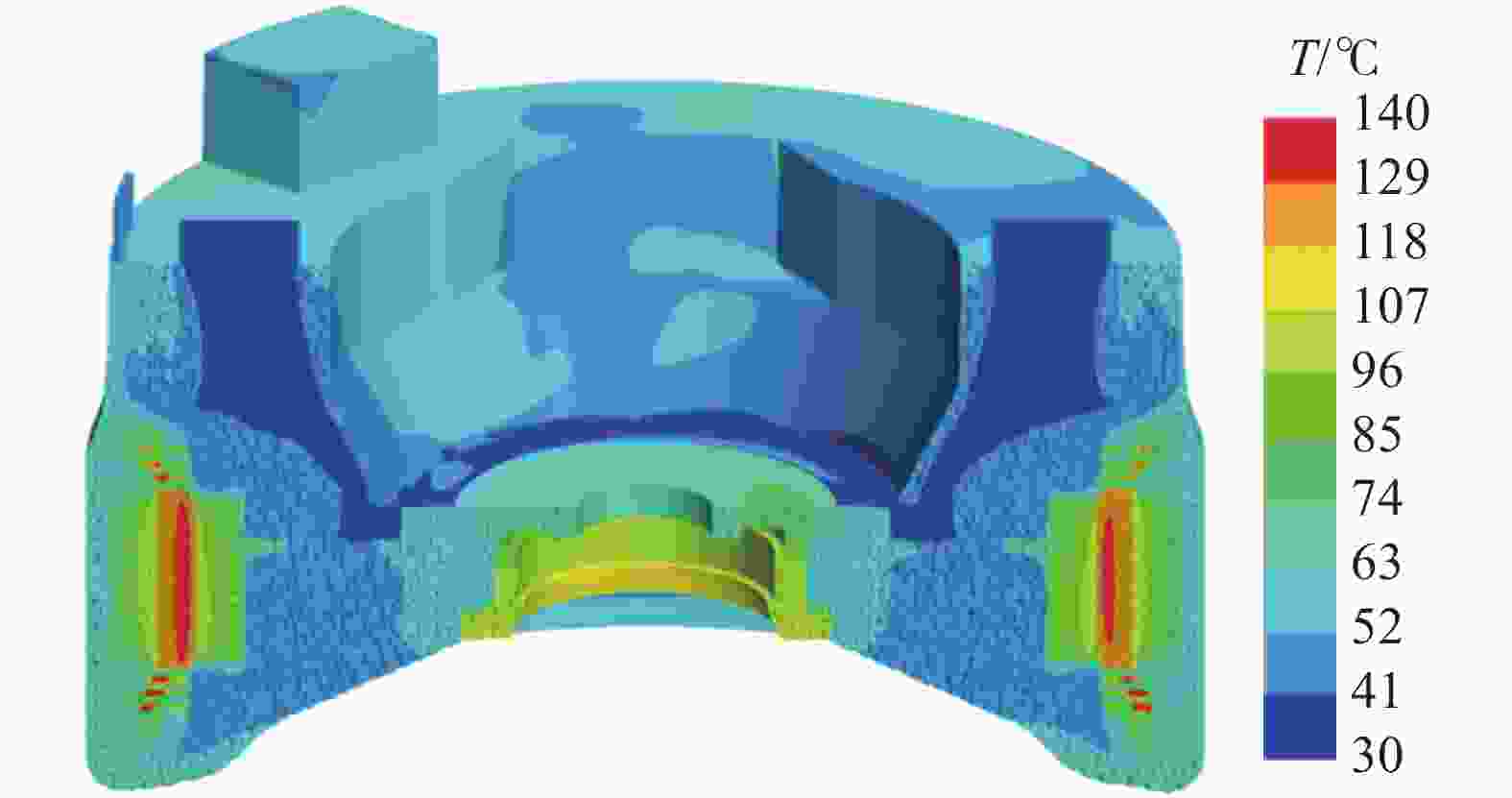
图6为发电机内部温度分布。从图中可以看出，发电机内部温度呈四周高中间低的趋势，这是因为端盖开孔向发电机中部区域输送冷风，降低了发电机中间区域温度。各部件中，绕组温度最高，定子铁芯次之，这是因为定子铁芯、绕组是发电机内的主要发热元件。

Figure 6.  Internal temperature distribution of generator

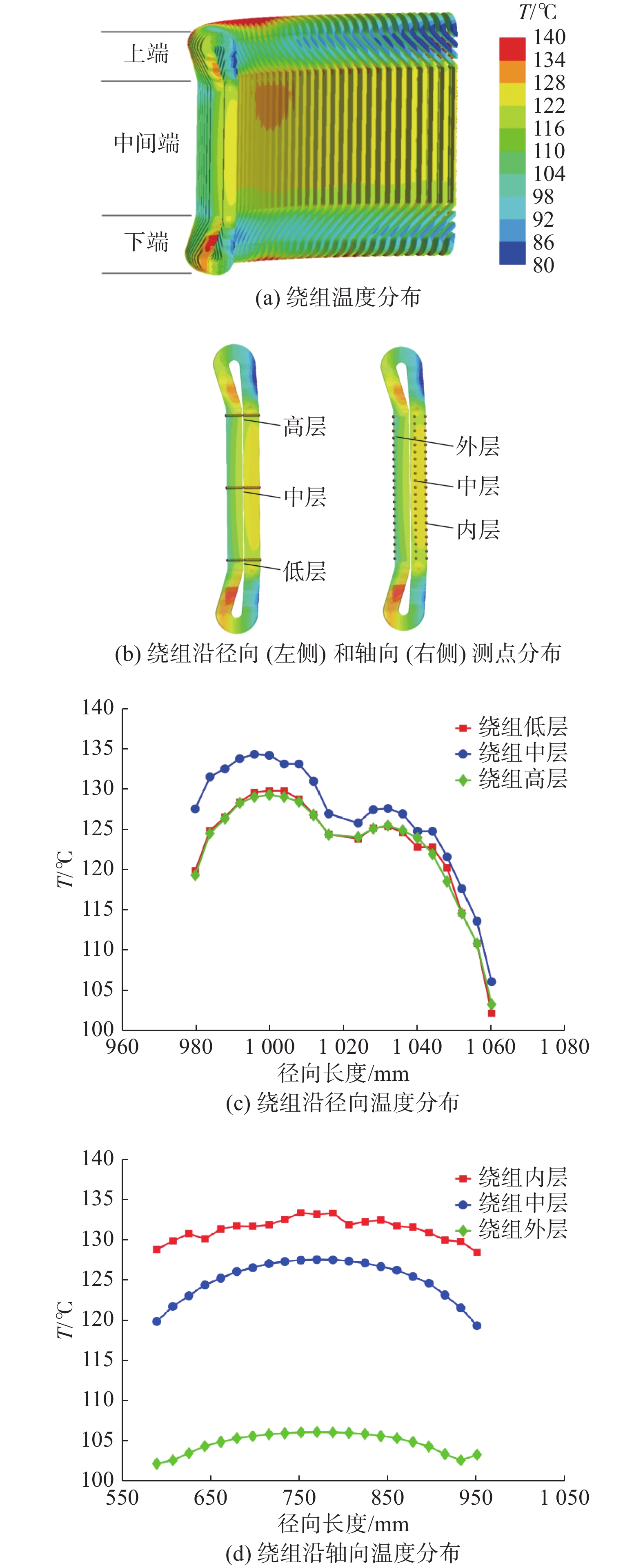
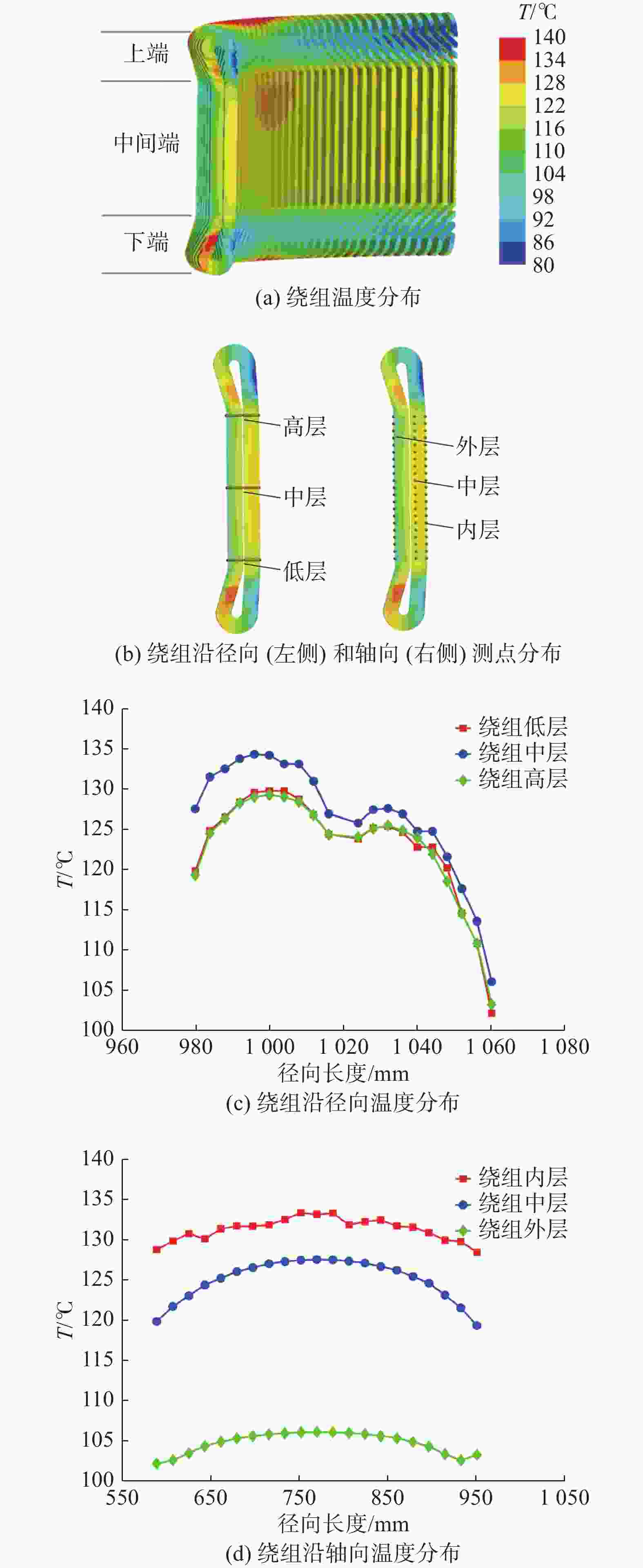
图7（a）为绕组温度分布图。绕组中间段与上、下端部温度分布规律存在明显差别。结合图7（a）、图7（d）知，绕组中间段内，外侧温度较内侧温度更低，这是因为定子铁芯装配有水冷系统，冷却水管与定子铁芯能量交换带走大量的热，绕组外侧距水管更近，换热效率更高，故绕组外侧温度更低。而绕组上、下端部区域内，内侧温度较外侧温度更低，这是因为受冷空气进风和转子旋转的影响，气流在发电机中部旋转，绕组内侧对流换热效果更好。

Figure 7.  Winding temperature distribution characteristics

为详细分析绕组内各区域温度分布规律，在绕组的中间段区域内，沿径向在低层、中层以及高层各布置20个温度测点，沿轴向在内层、中层以及外层各布置20个温度测点。如图7（b）所示。

从图7（c）中可知，随着径向距离的增大，绕组温度整体呈先增大后减小的变化趋势。这是因为当径向距离较小时，绕组靠近气隙、转子铁芯，而气隙、转子铁芯的温度均低于绕组温度，对绕组有一定的冷却作用。随着径向距离的增大，绕组换热效率逐渐降低，温度逐渐上升并达到最大值。当距离冷却水管较近时，绕组温度迅速降低，且距离冷却水管越近温度下降速度越快。绕组温度变化曲线存在下凹部分，这是因为该区域定子铁芯温度较绕组低，绕组外表面包裹绝缘层，绝缘层导热性能较差，换热不充分，因此存在较大的温度梯度。

结合图7（c）、图7（d）知，沿径向方向，绕组低层、高层温度相差不大，绕组中层较低、高层的温度更高，最大温差达28.1℃。这是因为绕组中层的散热方式仅包含固体之间的热交换，而绕组低、高层的散热方式还包括固体和气体之间的热传递，散热效率更高，故低层、上层的温度更低。由上述分析可以总结出，在发电机的制造过程中，冷却水管位置应尽可能靠近绕组，以带走更多的热量。

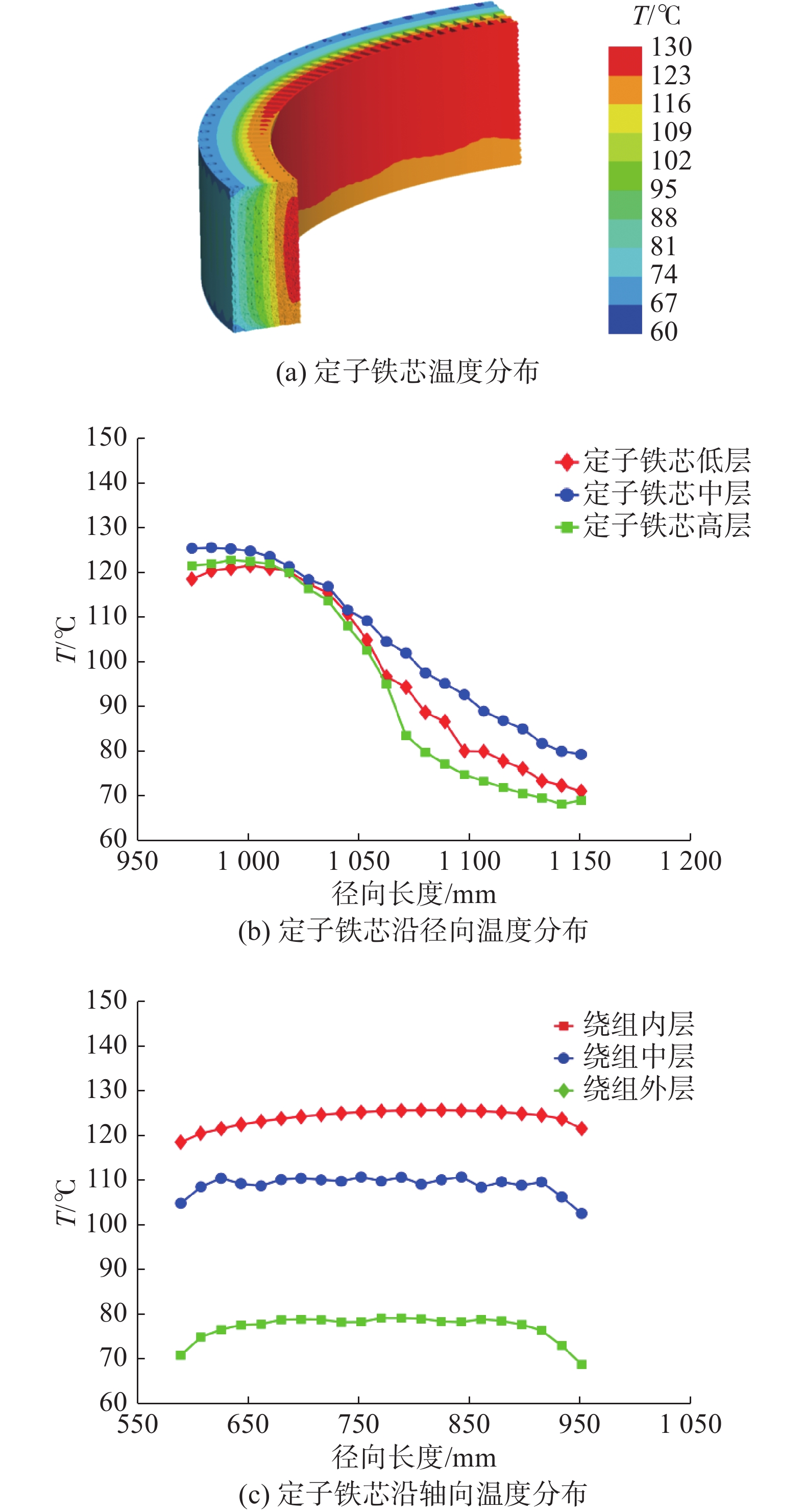
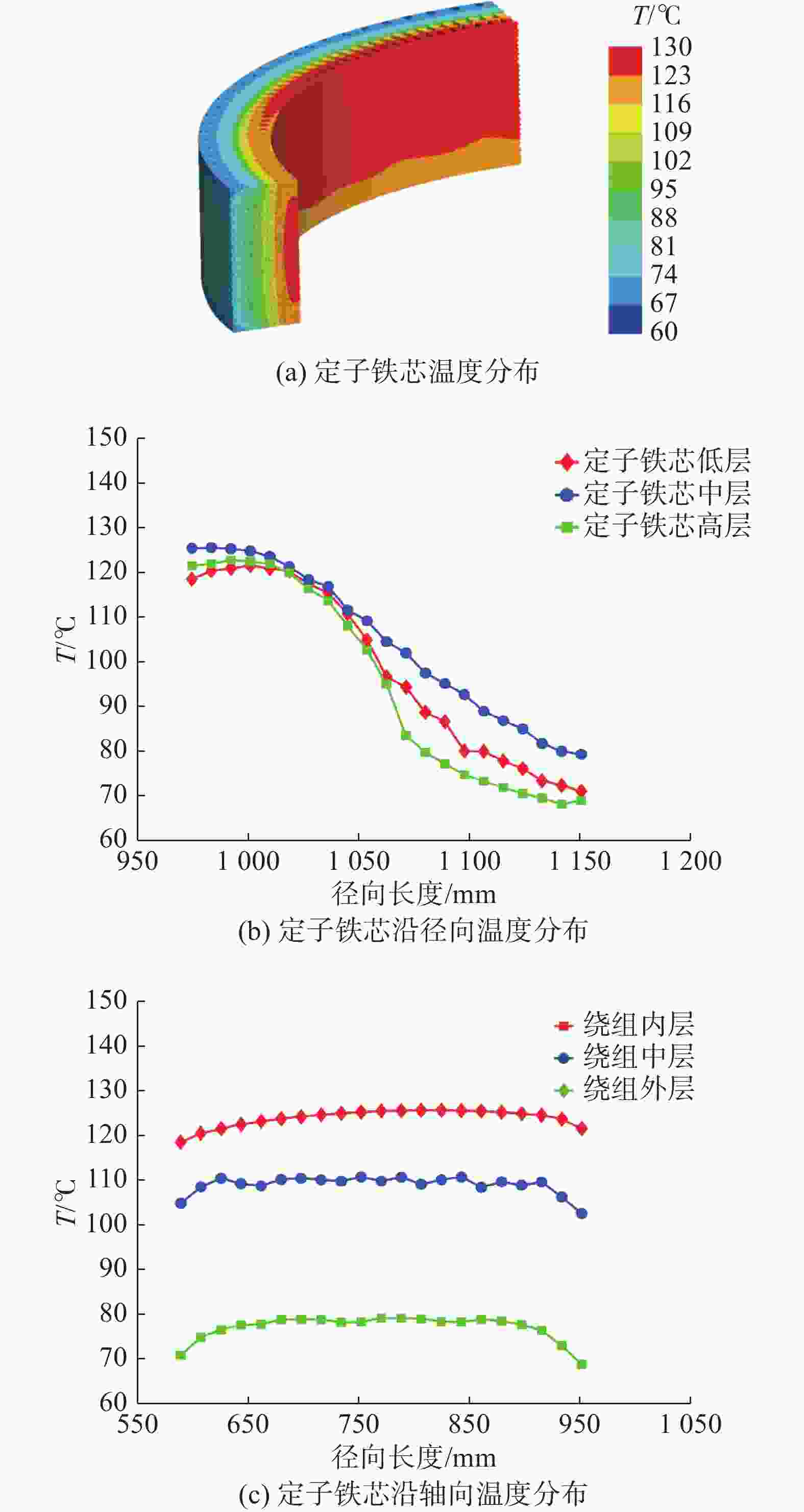
为详细分析定子铁芯内各区域温度分布规律，沿径向在定子铁芯低层、中层以及上层各布置20个温度测点，沿轴向在定子铁芯内层、中层以及外层各布置20个温度测点，铁芯测点位置布置方式参照绕组。

结合图8（a）、图8（b）知，3个层面的定子铁芯温度变化规律相同，均随径向距离的增大温度逐渐降低，这是因为定子铁芯外层装有冷却水管，冷却水流动带走了大量的热。定子铁芯中层温度较低层、高层温度更高，最大温差达53.1℃，产生该现象的原因与绕组一致。低层温度略高于高层温度，这是由于发电机底部空气流速较上部要小，换热效果较弱。由图8（c）知，定子铁芯温度沿轴向分为3个阶段，第一阶段为上升阶段，第二阶段为平稳阶段，第三阶段为下降阶段。这是因为位于中间部分的定子铁芯的换热方式主要是固体之间的热传导，而轴向距离较小或较大的位置处温度较低，这是因为此处热传递方式不仅包含固体之间的热传导，还包括定子铁芯与冷空气的对流换热。

Figure 8.  Temperature distribution characteristics of stator core

为研究发电机散热性能的影响因素，选取了风冷系统中的总进风量、进风温度以及水冷系统中的进水温度、冷却液属性、冷却水管与定子铁芯的间隙共5个参数进行分析，每个参数设有4组工况，总计20个工况，各工况具体参数如表4、表5所示。

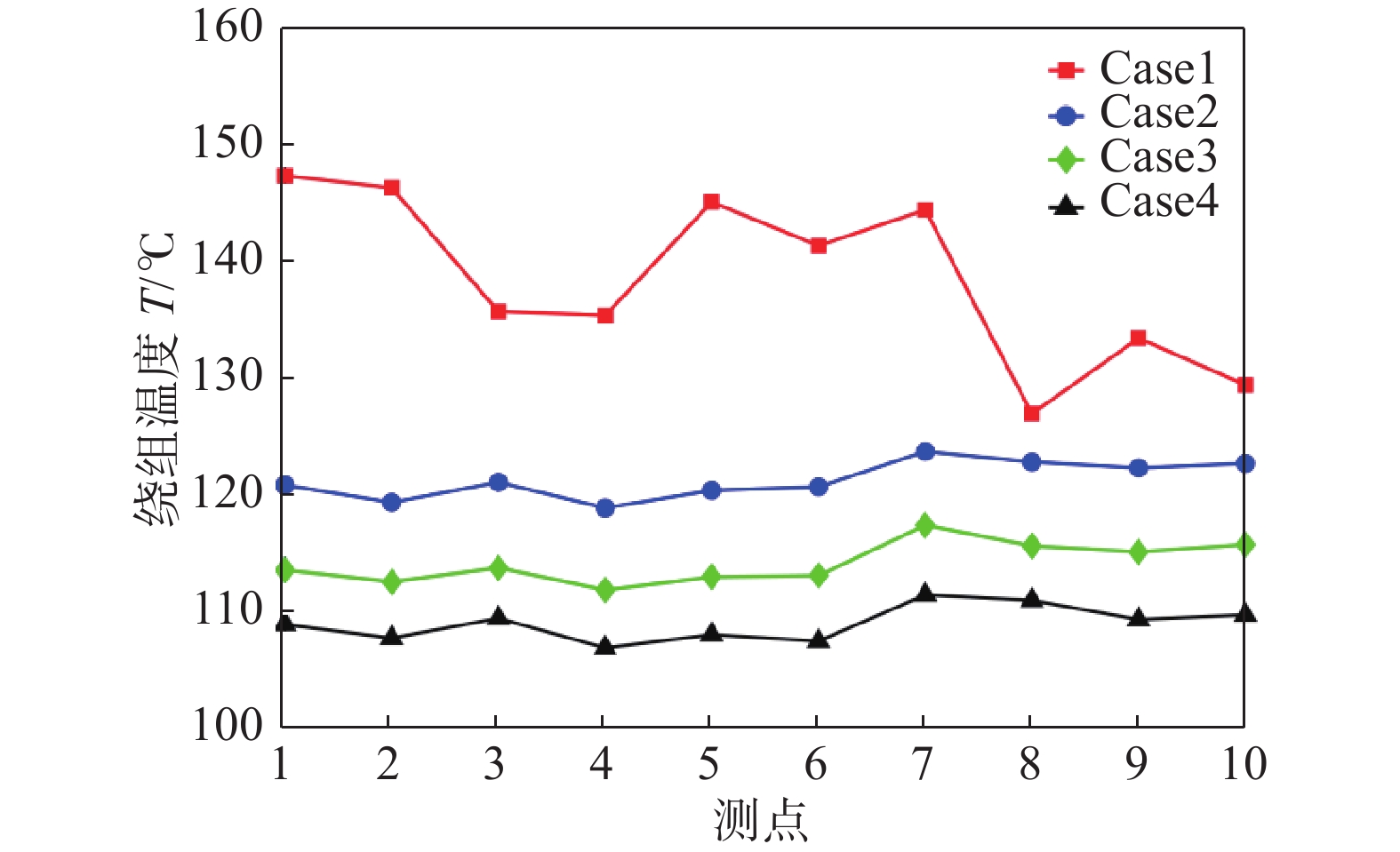
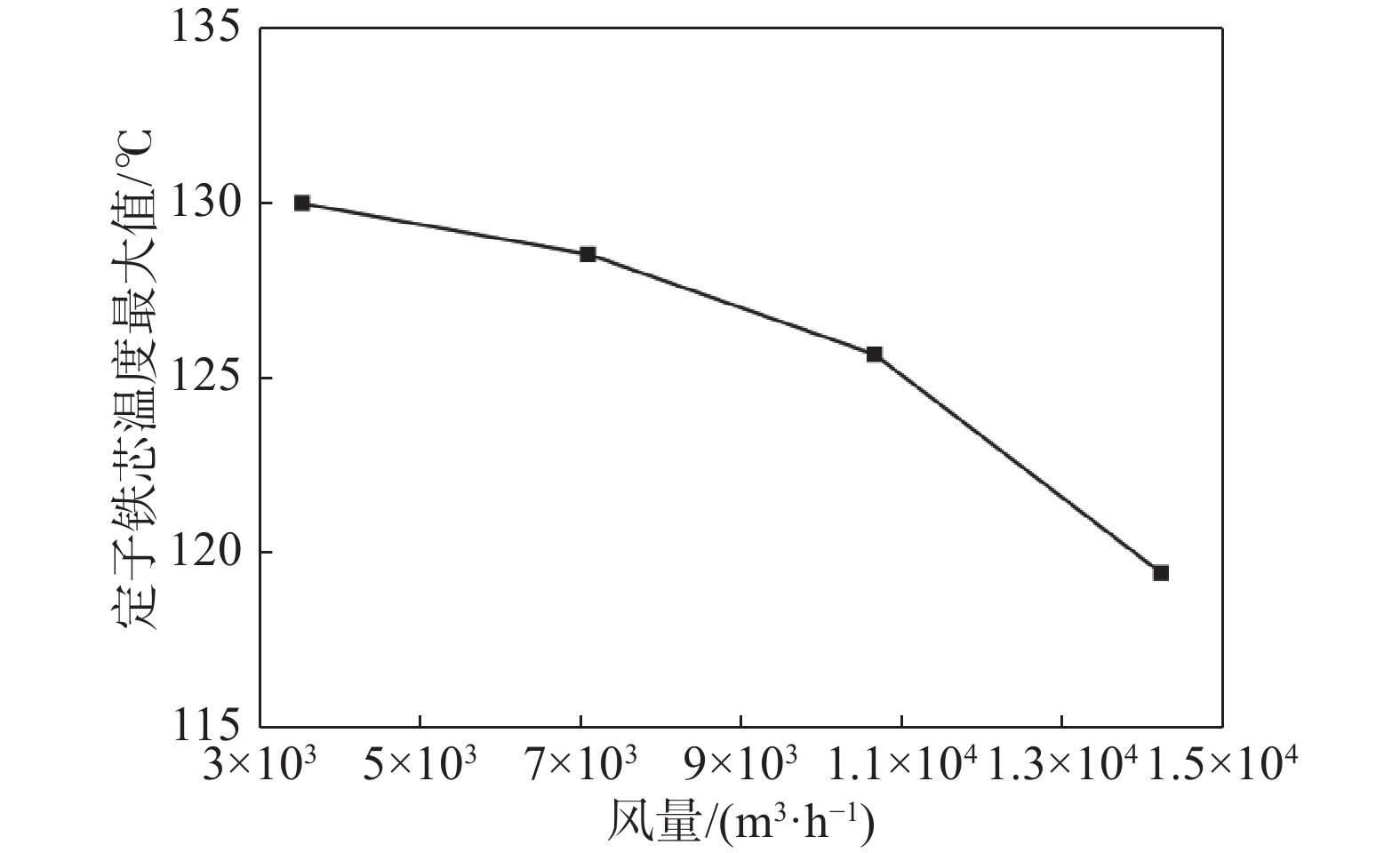
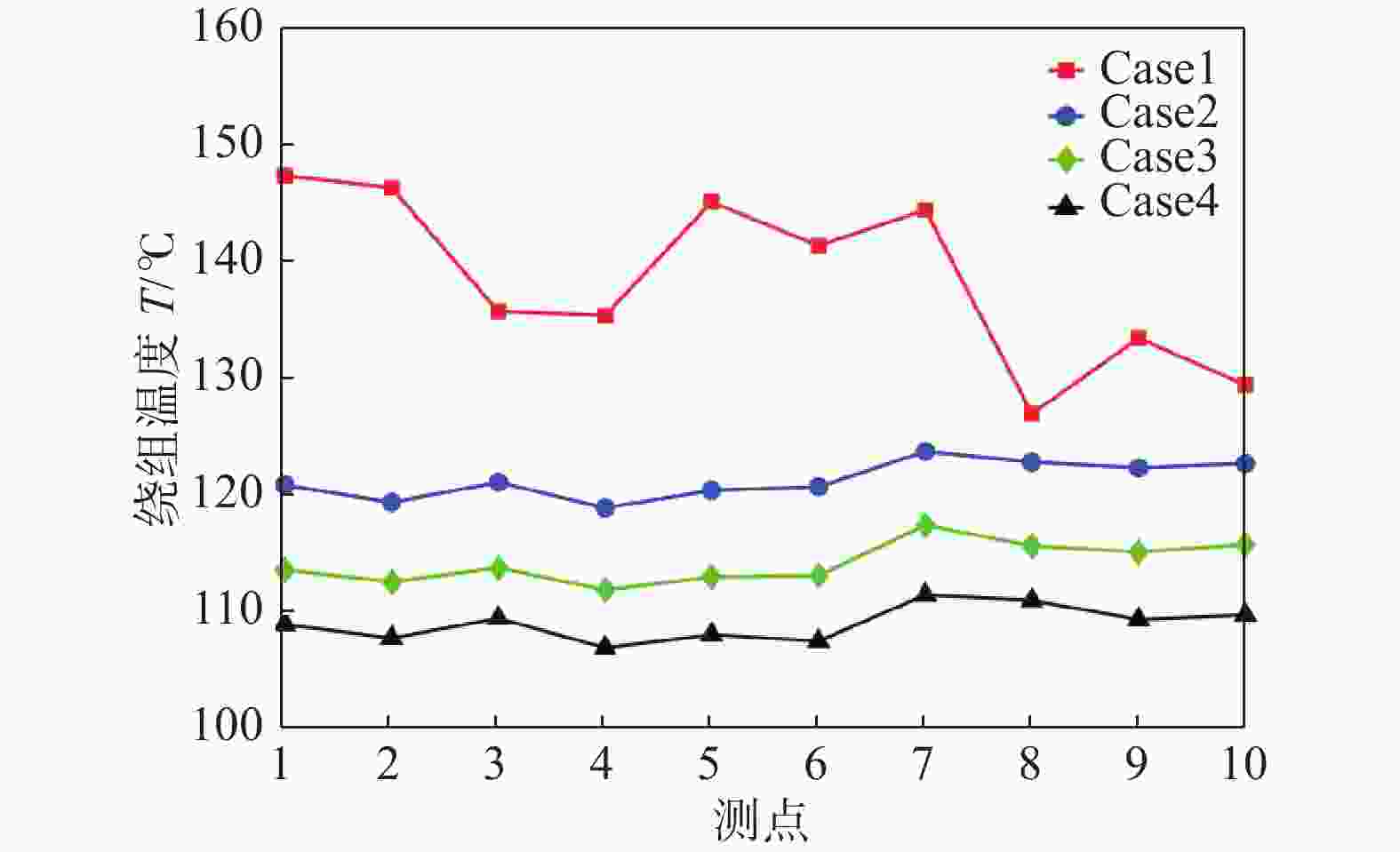
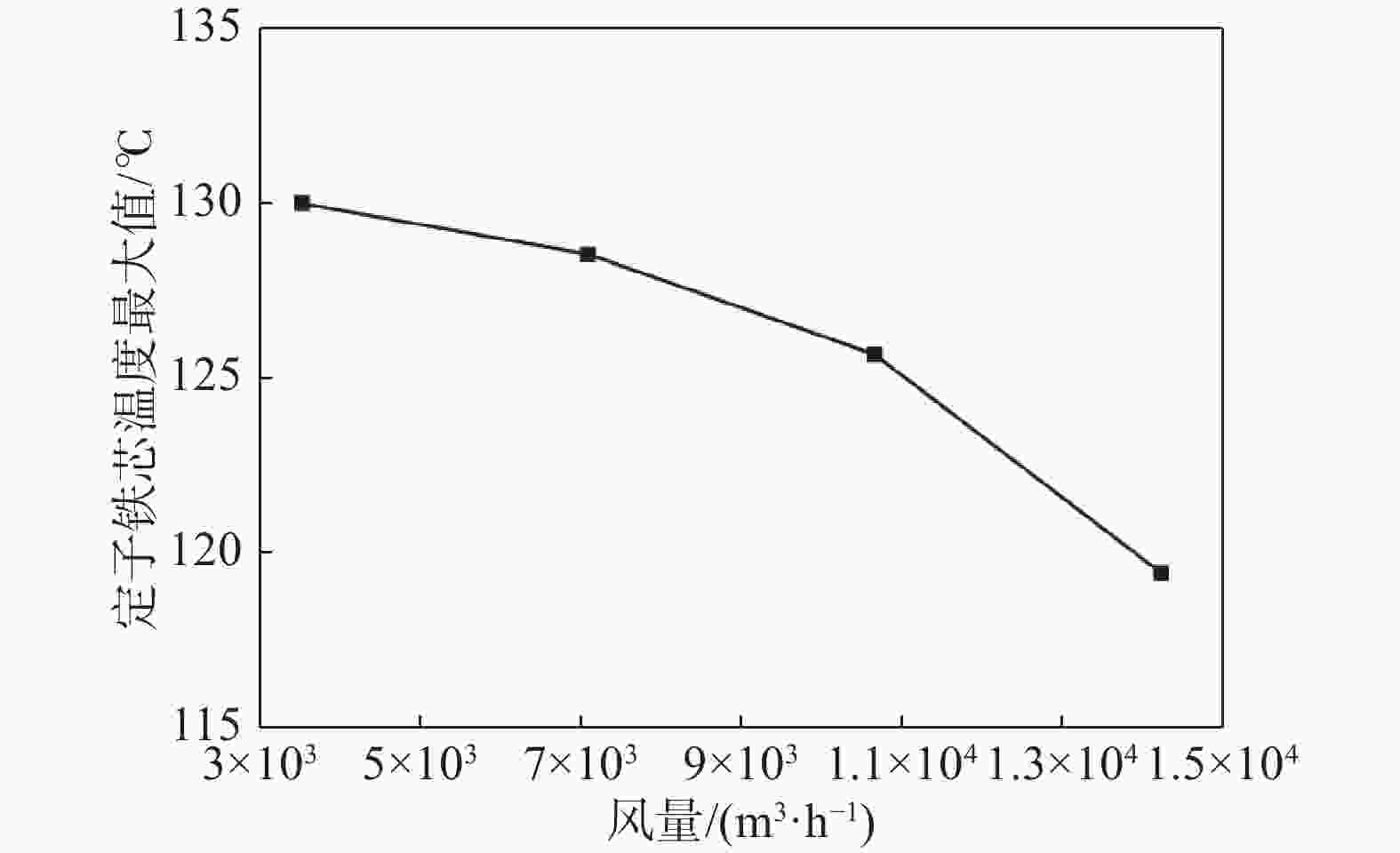
总进风量对绕组温度、定子铁芯温度的影响如图9、图10所示。横坐标中的测点1~10与实验布置的测点1~10位置一致。从图中可以看出，进风量对发电机散热情况影响显著，当总进风量为3 550 m³/h时，绕组测点最高温度为147.2 ℃，总进风量为14 200 m³/h时，绕组测点最高温度为111.6℃，最高温度降低了35.6 ℃。可见，总进风量增大后，发电机散热情况明显改善。结合图9、图10知，随着总进风量的增大，绕组温度降低速率逐渐减小而定子铁芯最高温度下降速率逐渐增加，这是因为定子铁芯完全包裹住了绕组中间段，定子铁芯绝大部分面积能够与空气进行换热，而绕组的换热能力受限。当总风量较低时，换热效果较差，主要原因包括两部分，首先进风量降低直接导致换热量不足，其次进风量低导致进风口流速较低，发电机内气流湍流度低，换热效果减弱，这说明提高散热器功率更有利于发电机散热。

Figure 9.  Influence of total intake air volume on winding temperature

Figure 10.  Influence of total intake air volume on stator core temperature

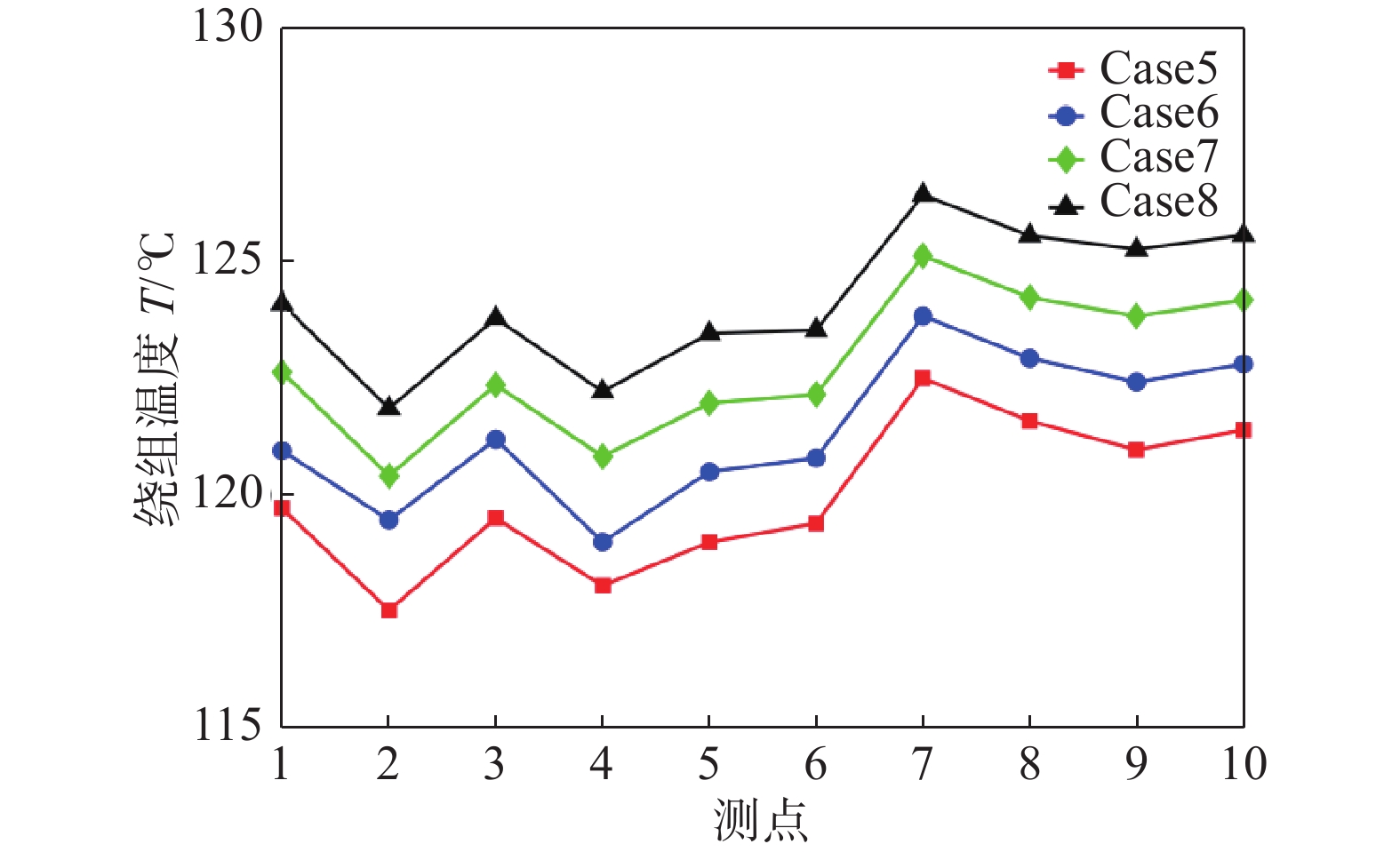
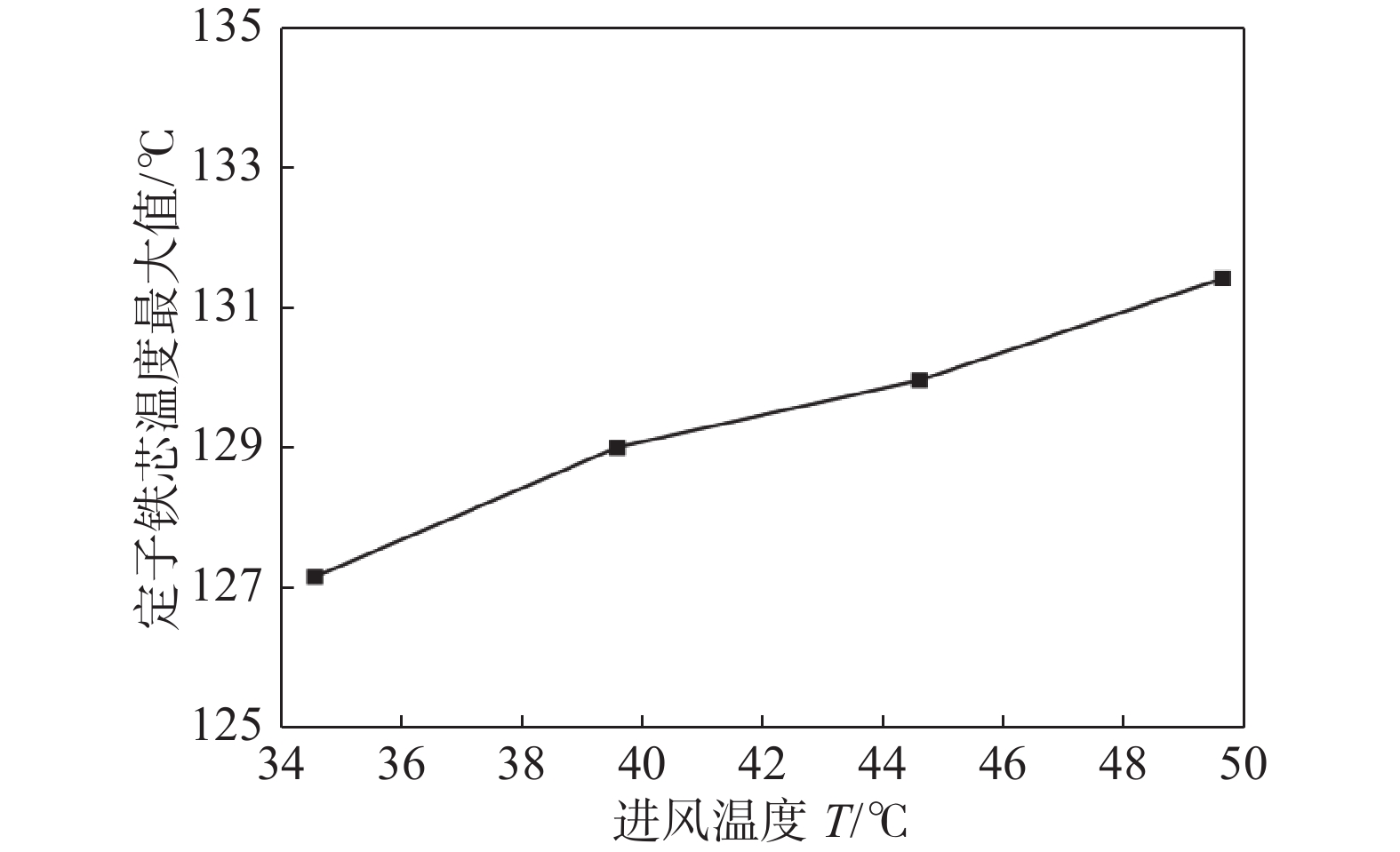
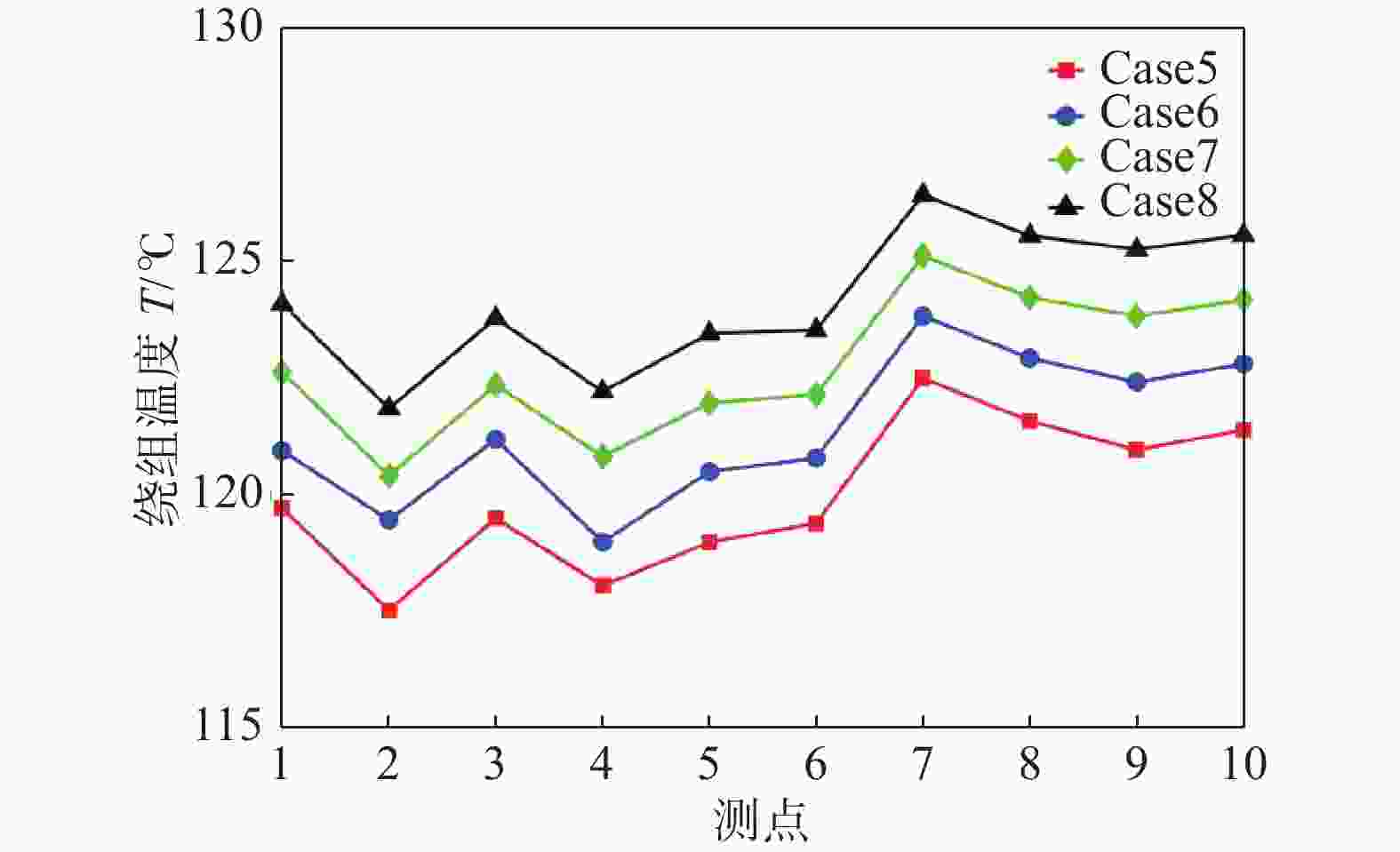
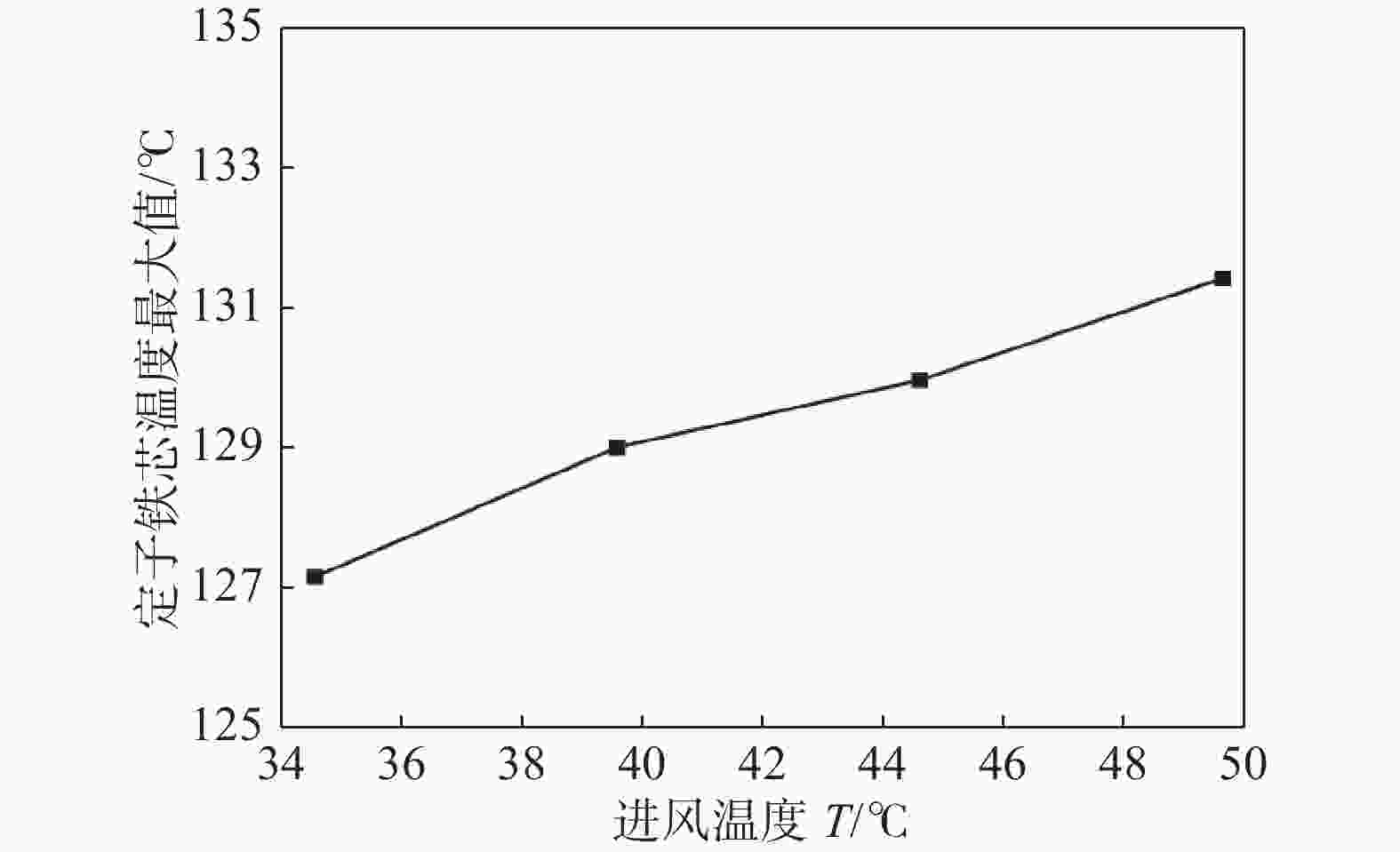
进风温度对绕组温度、定子铁芯温度的影响如图11、图12所示。由图知，随着进风温度的降低，绕组、定子铁芯的最高温度均有所减小，当进风温度由49.6 ℃降低至34.6 ℃时，绕组、定子铁芯最高温度降低4.2 ℃，且进风温度与绕组、定子铁芯最大温度呈线性关系，每降低5 ℃，绕组、定子铁芯最大温度降低约1.4 ℃，这说明降低进风温度可一定程度上改善发电机散热效果。极限工况下，发电机进风温度较高，可先对热风进行冷却处理，使进入发电机内的空气满足温度要求，以降低发电机热载荷。

Figure 11.  Influence of intake air temperature on winding temperature

Figure 12.  Influence of intake air temperature on stator core temperature

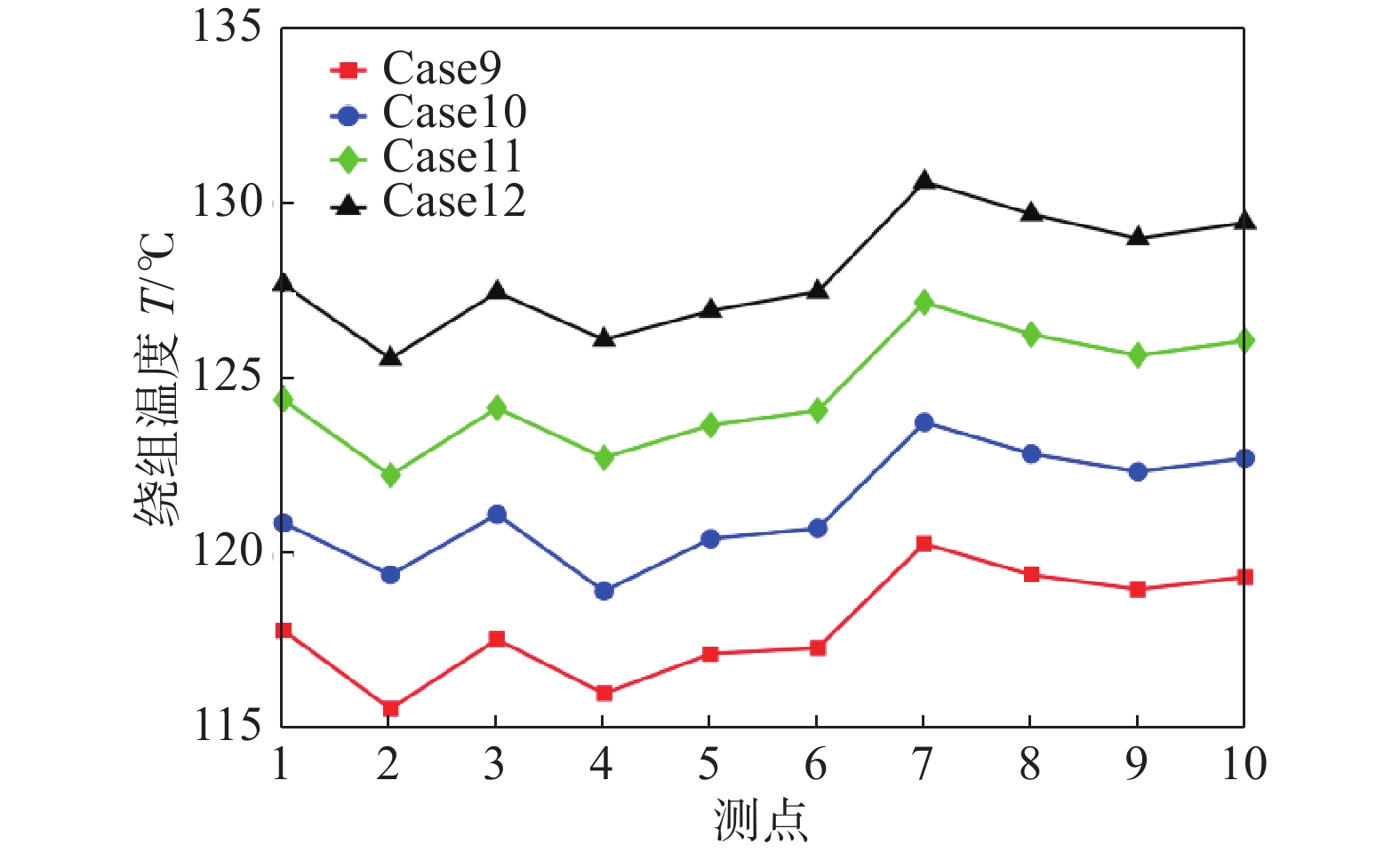
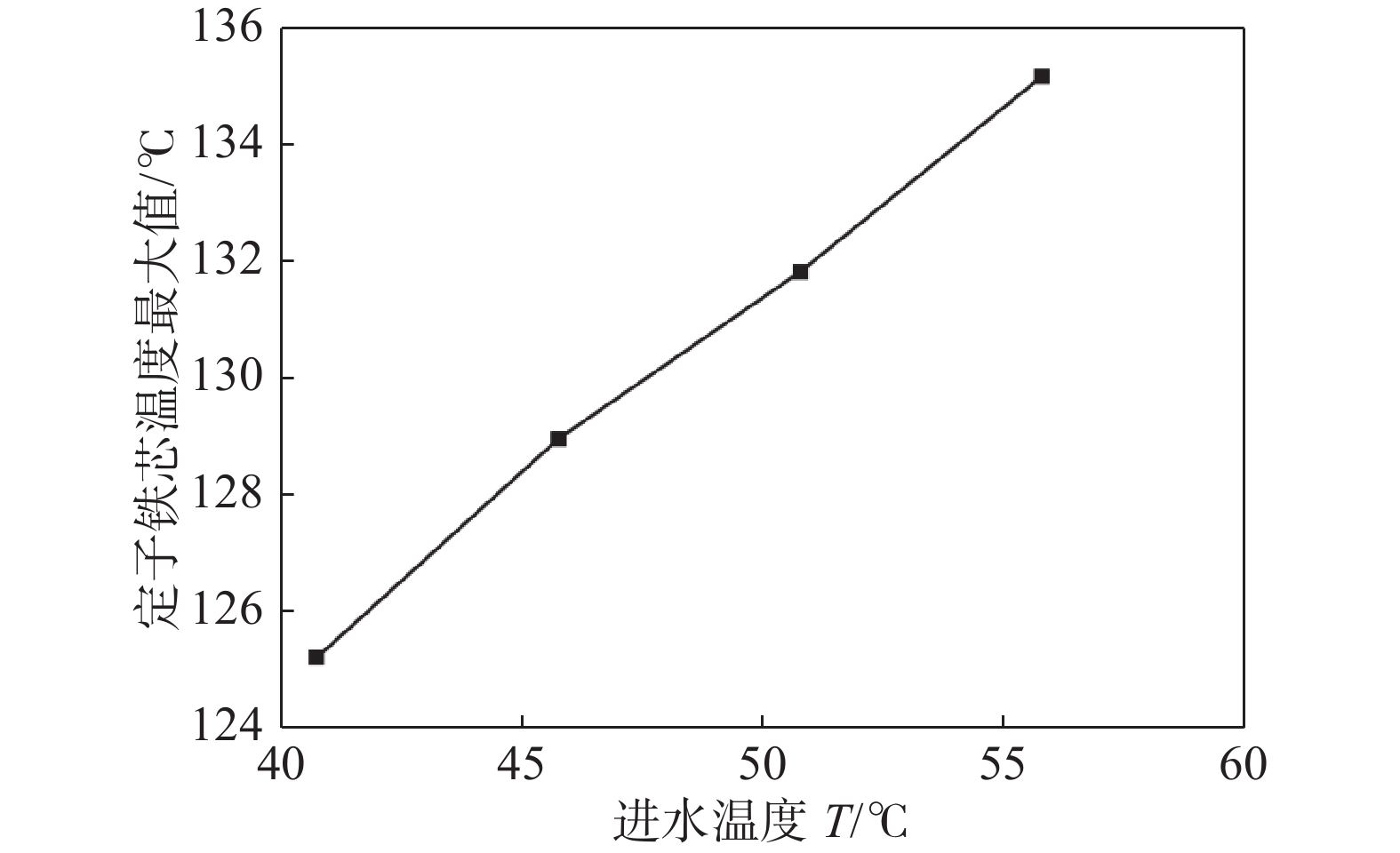
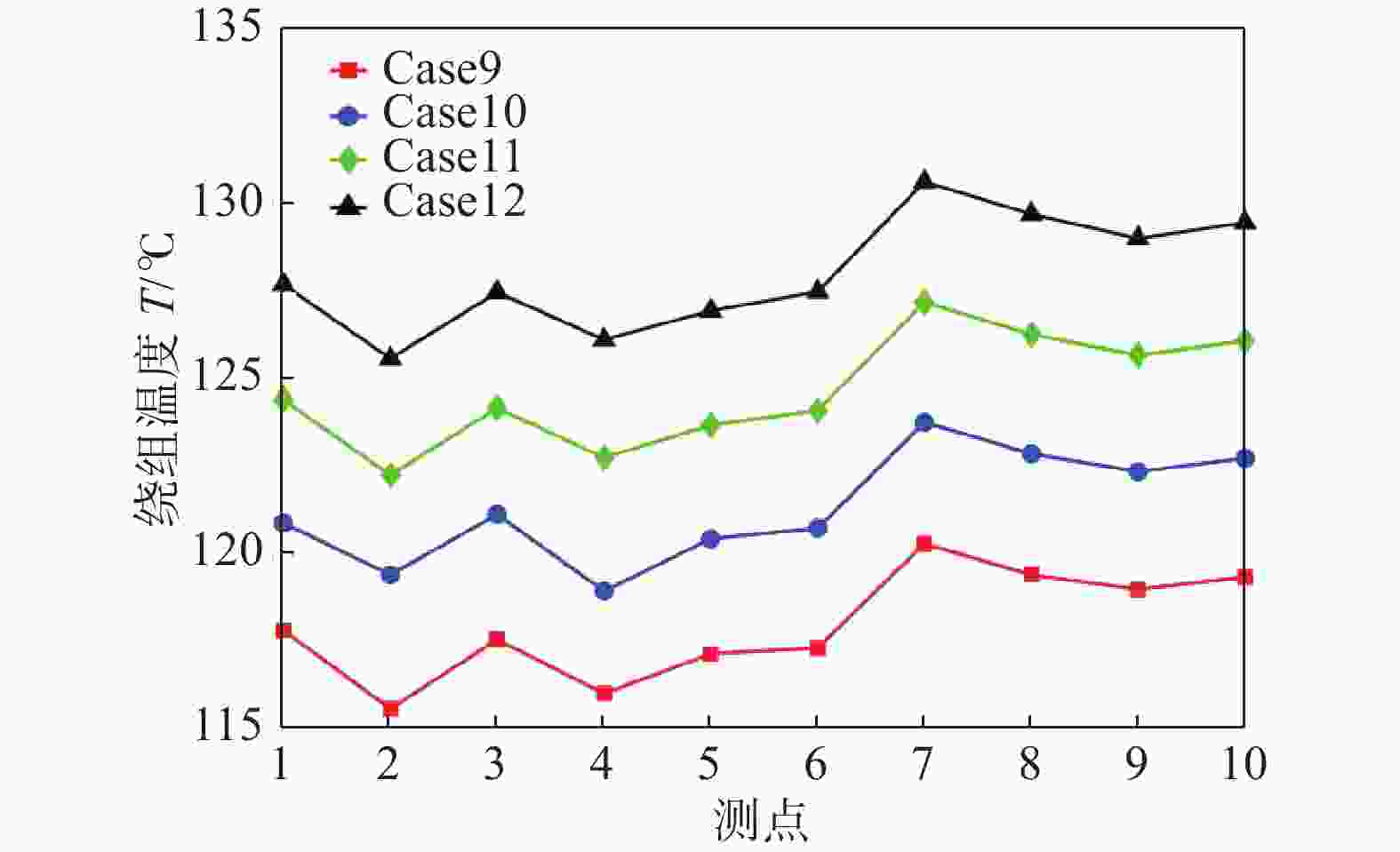
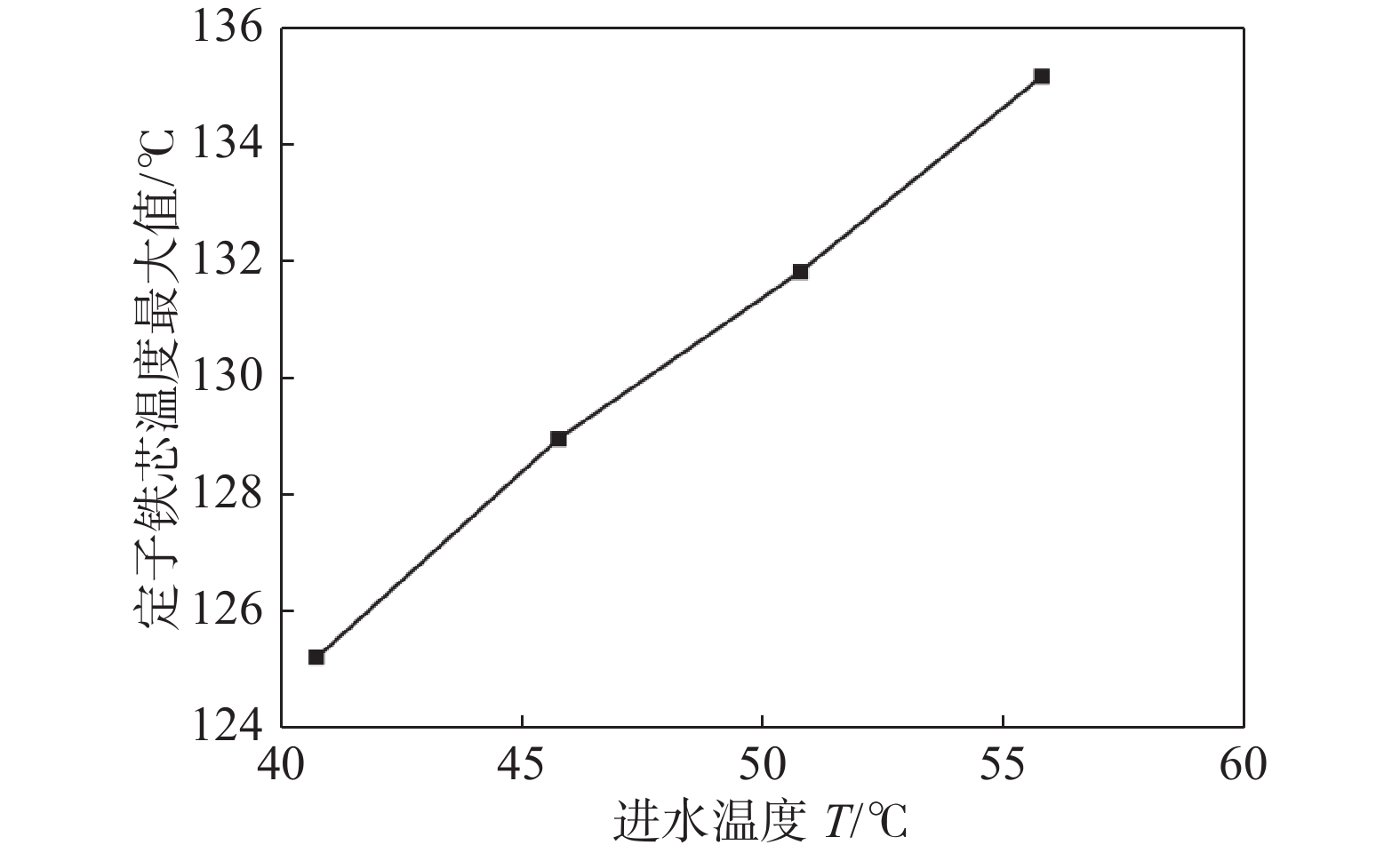
图13、图14给出了进风温度对绕组温度、定子铁芯温度的影响。进水温度降低时，绕组、定子铁芯温度下降明显。当进水温度由55.8 ℃降低至40.8 ℃时，发电机最高温度降低了约10 ℃。同时，进水温度与绕组、定子温度呈线性关系，水温每降低5 ℃，绕组、定子铁芯最大温度降低约3.3 ℃，说明降低进水温度可显著改善发电机散热性能。

Figure 13.  Influence of water intake temperature on winding temperature

Figure 14.  Influence of intake water temperature on stator core temperature

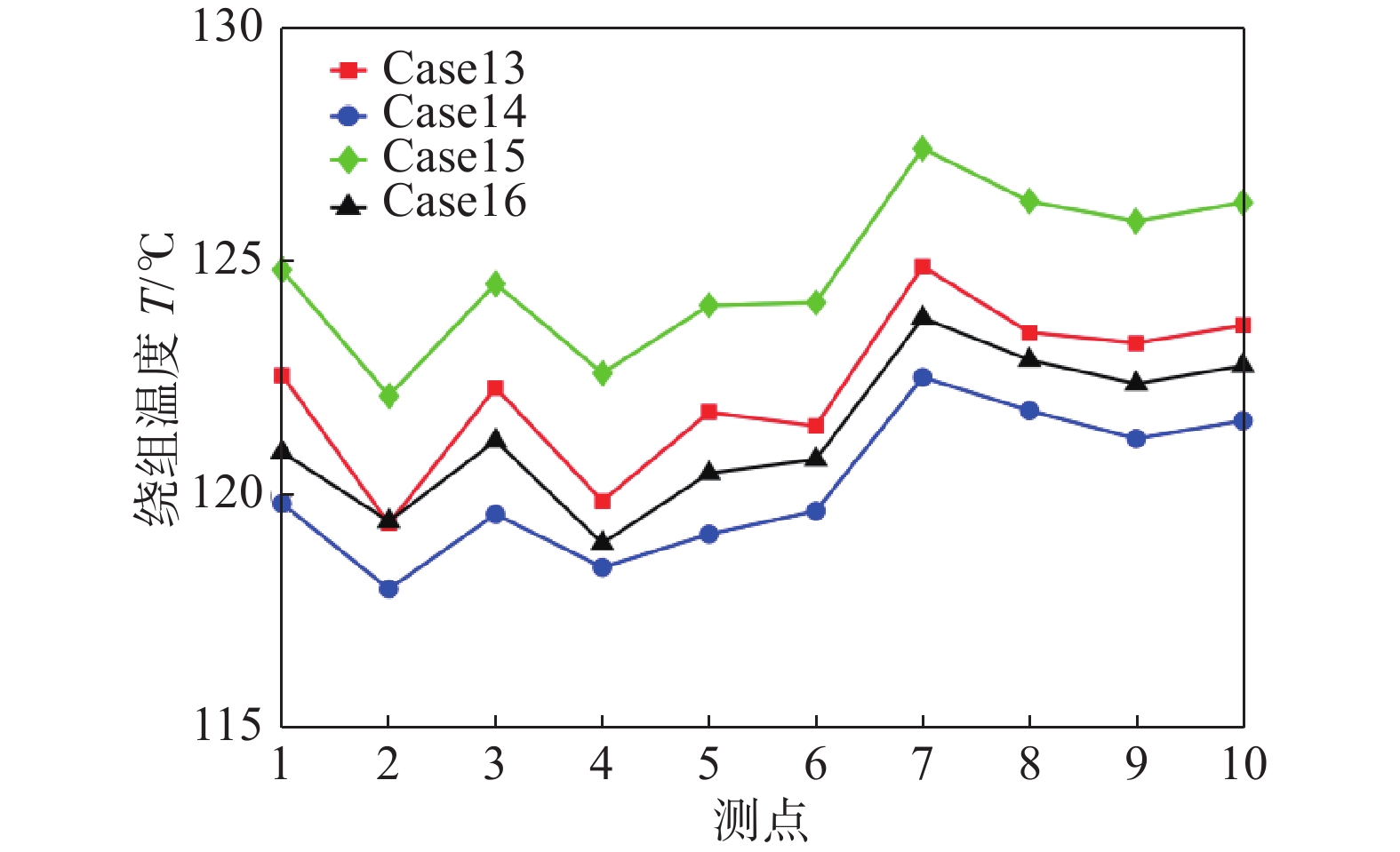
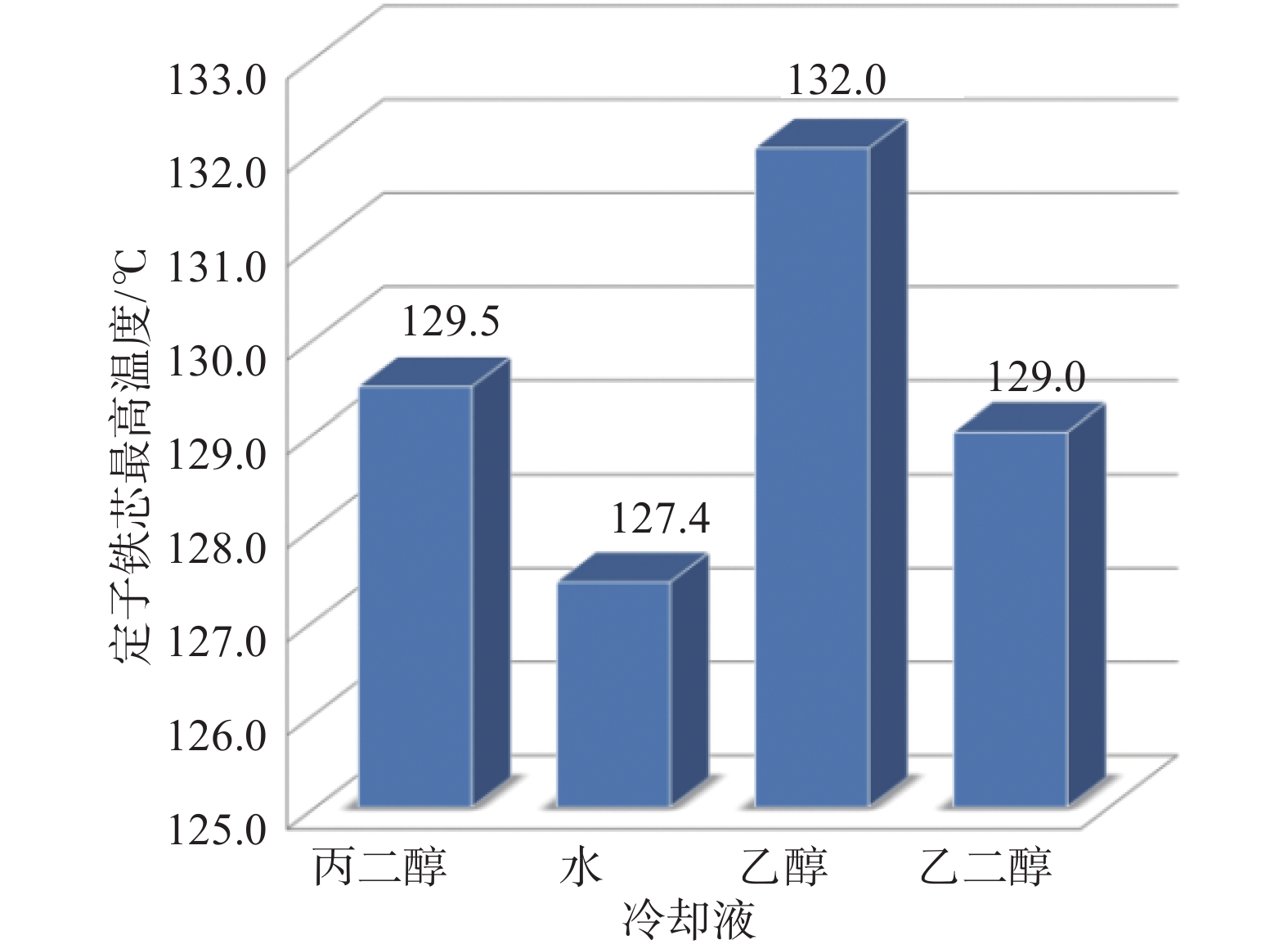
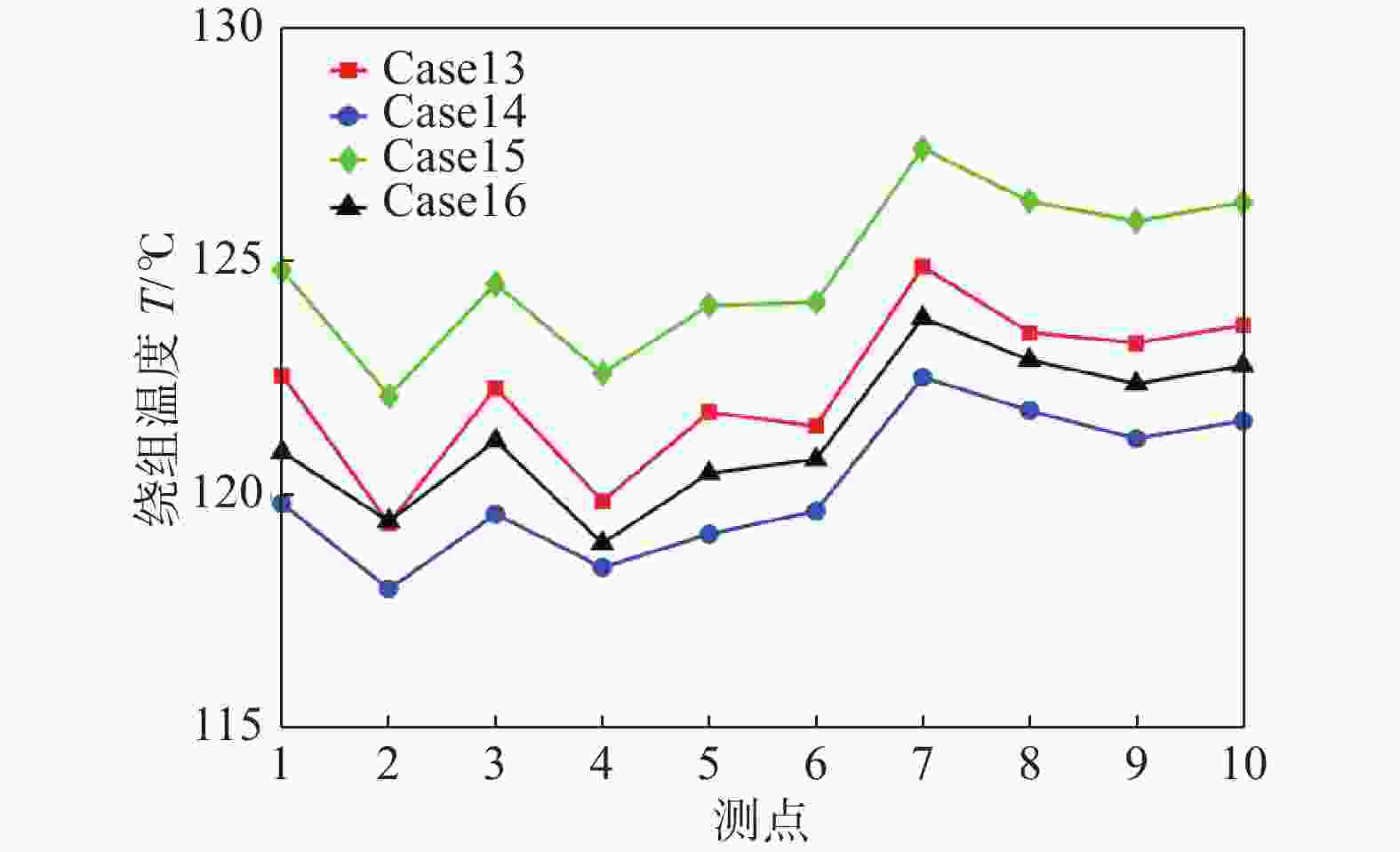
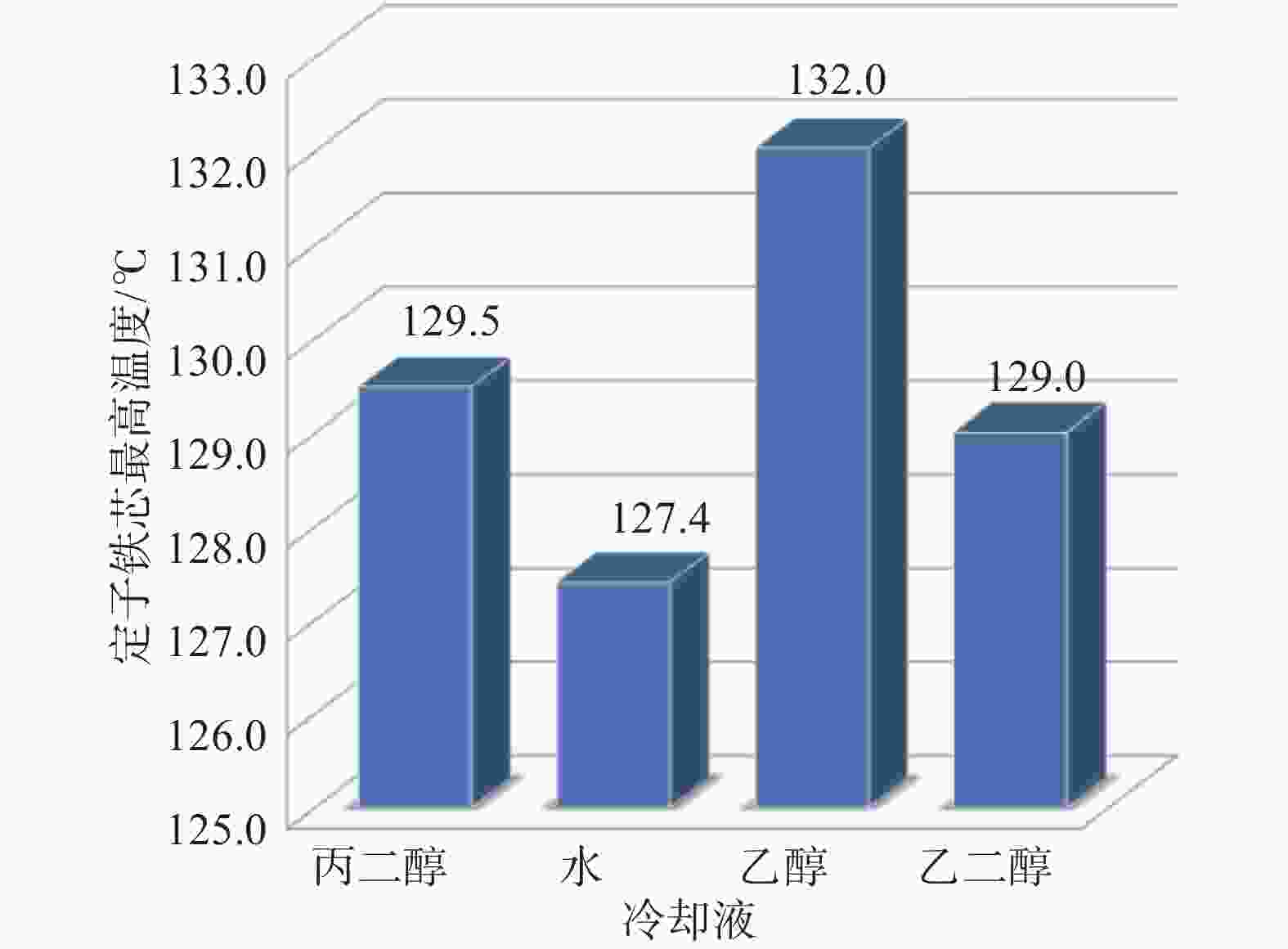
图15、图16给出了4种冷却液对绕组温度、定子铁芯温度的影响。从图中可以看出，相同条件下，水的冷却效果最佳，乙醇的冷却效果最差，这是因为水的热容大、导热系数高，而乙醇恰好相反。根据不同区域环境温度的差别，风力机一般分为常温型和低温型。低温型风力发电机一般布置于寒冷区域，温度可达零下30℃，因此冷却液的冰点须足够低，4种冷却液中乙二醇的凝固点最低，抗冻性能好，并且冷却效果较好，可作为低温区的冷却液使用，其余3种冷却液可作为常温机型的冷却液使用。

Figure 15.  Influence of different coolants on winding temperature

Figure 16.  Influence of different coolants on stator core temperature

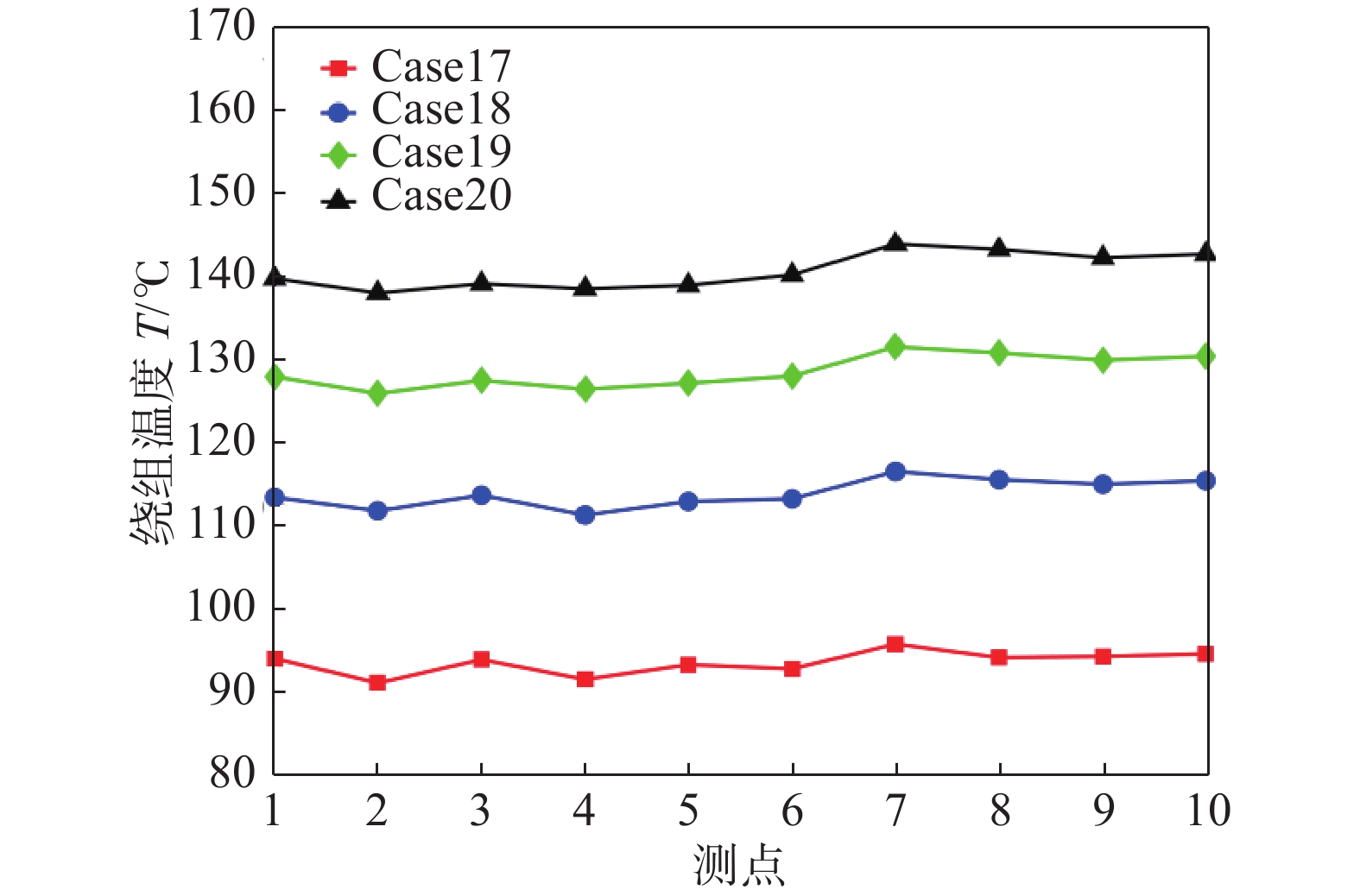
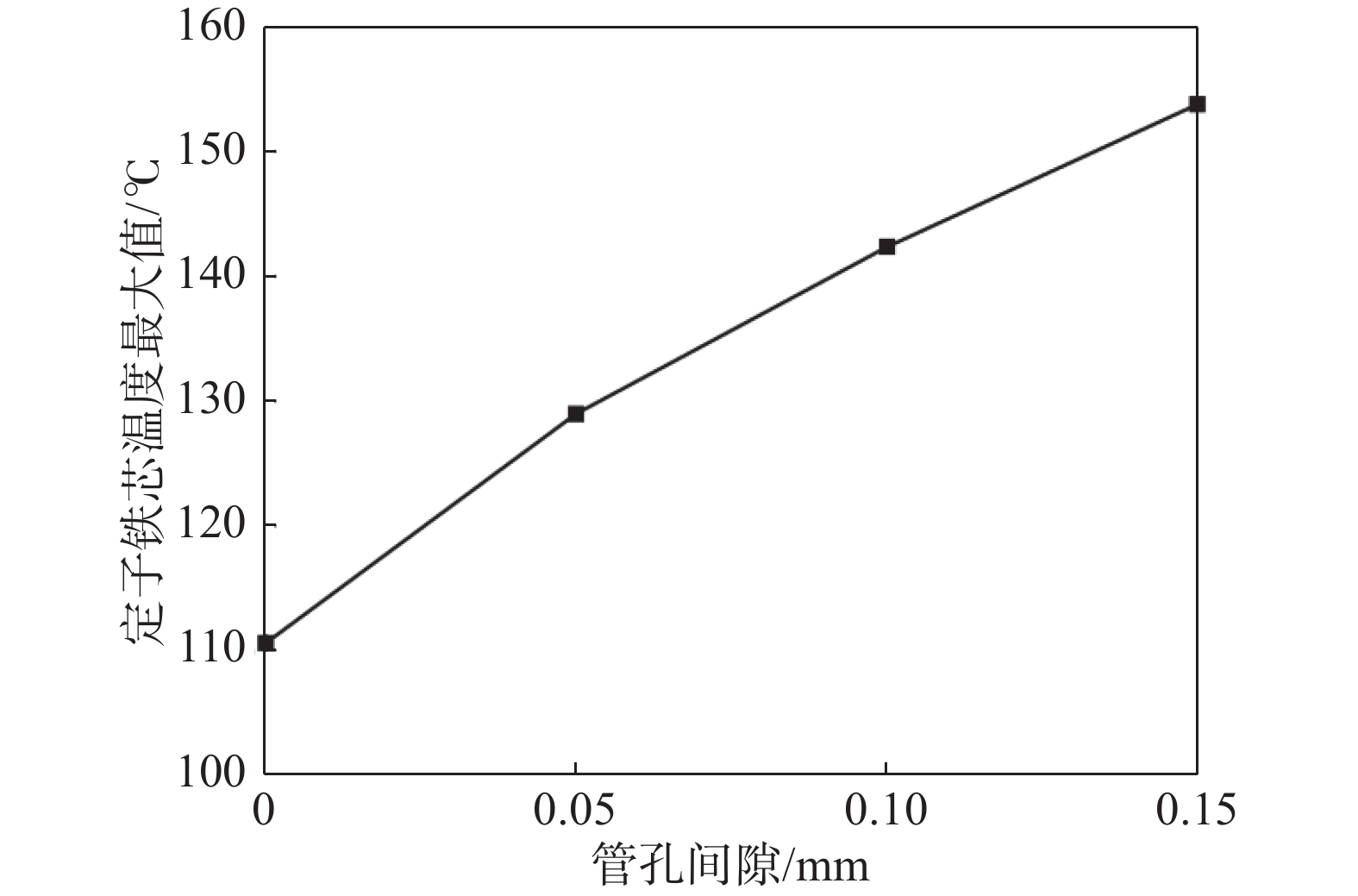
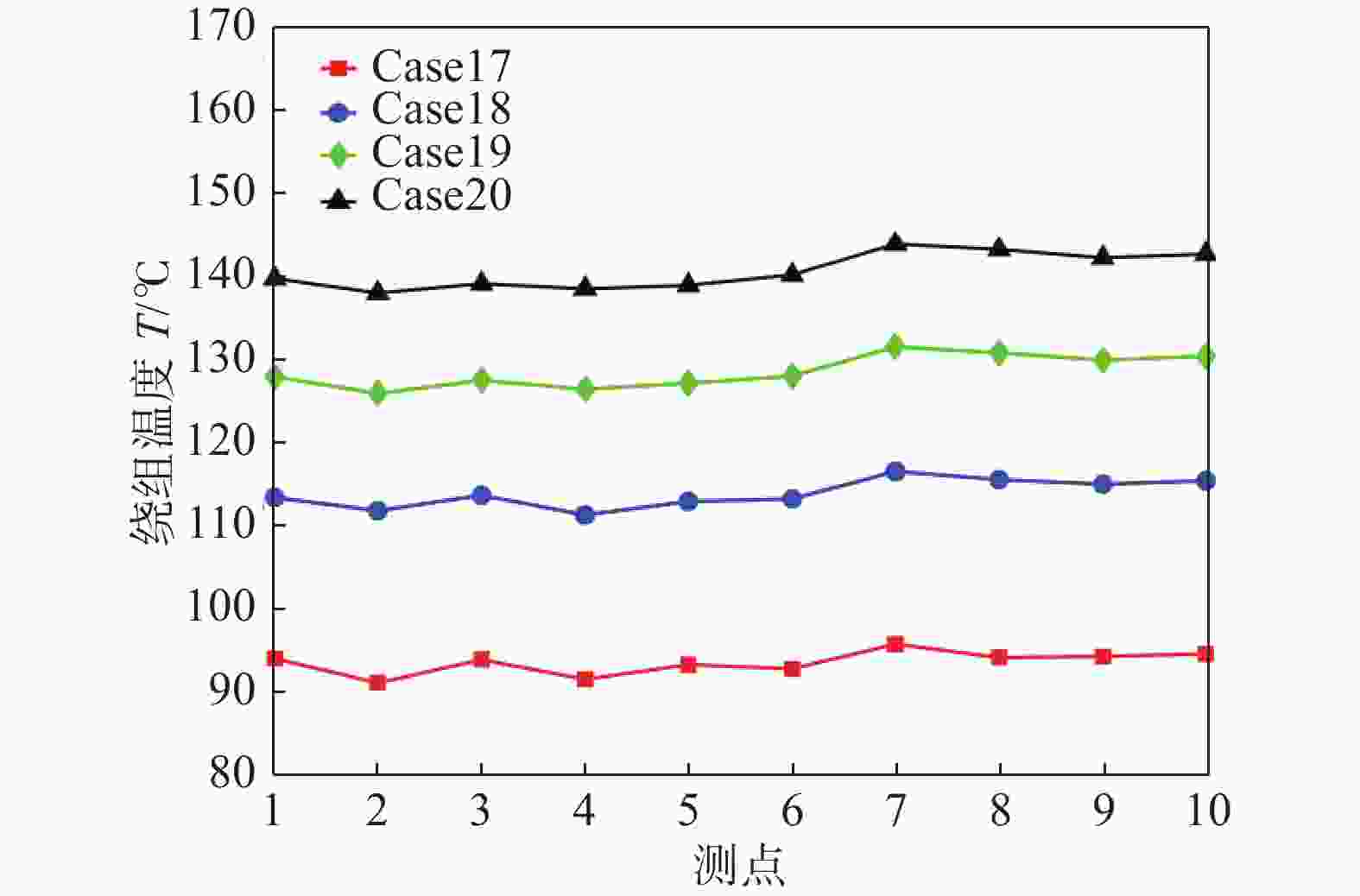
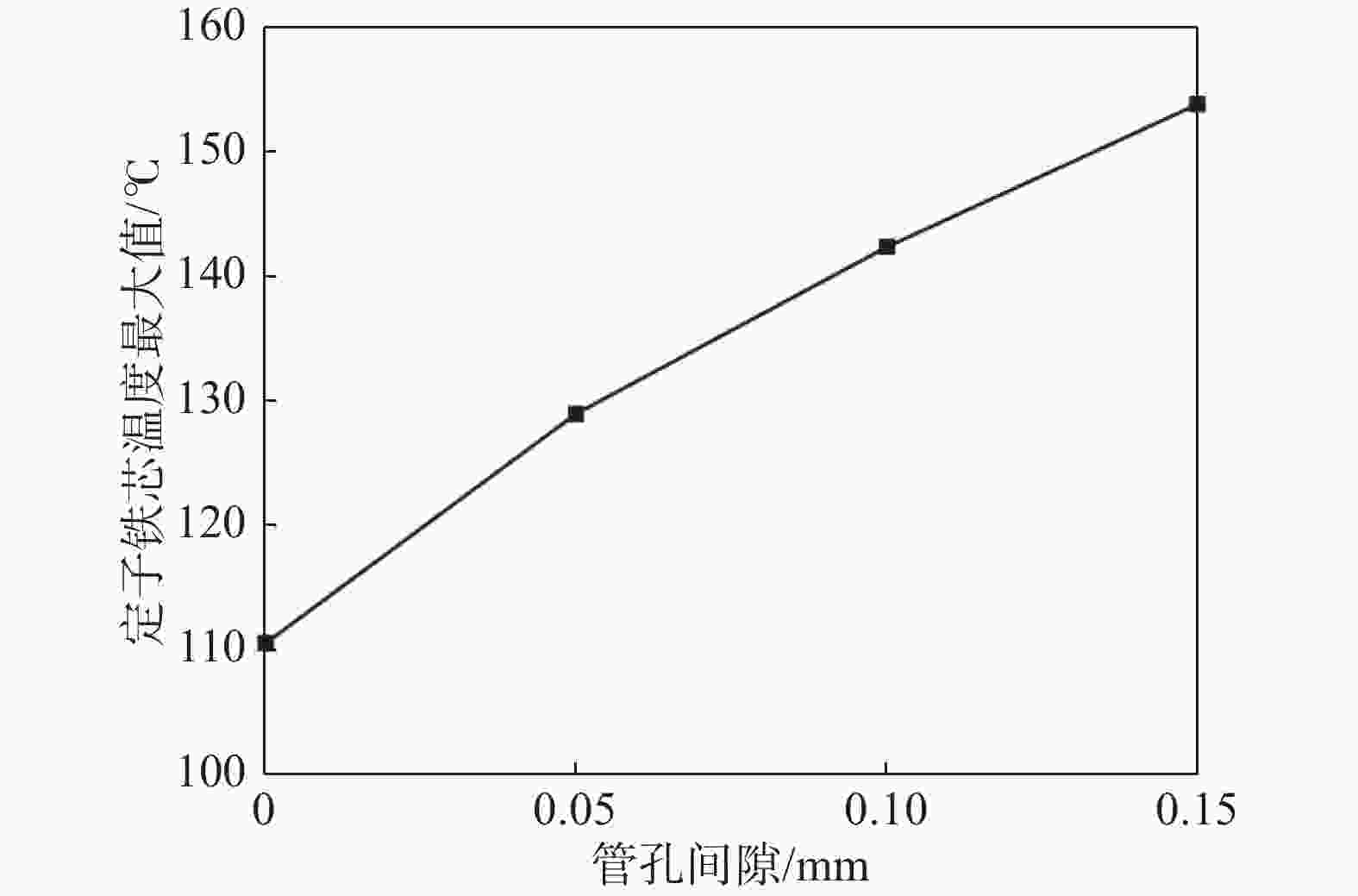
定子铁芯由硅钢片叠压而成，受冷却水管、定子铁芯表面粗糙度以及组装工艺精度的影响，装配过程中，冷却水管与定子铁芯之间会存在间隙，即管孔间隙，间隙大小对绕组温度、定子铁芯温度的影响如图17、图18所示。从图中可以看出，间隙对发电机散热效果影响显著。当管孔间隙为0 mm时，即冷却水管与铁芯完全接触时，测点最大温度为104.7℃；当管孔间隙为0.15 mm时，测点最大温度高达149℃。间隙每增大0.05 mm，测点温度上升数值超过10℃。可见，管孔间隙使得冷却水管换热受到极大的阻碍。产生该现象的原因是间隙的成分主要为空气，空气的热容以及导热系数极低，阻挡了定子与水管的换热。因此，在制造、装配工艺精度无法进一步改善的条件下，可以在间隙中填充导热材料，如导热硅脂等，降低间隙的热阻，增强冷却水管的换热效率。

Figure 17.  Influence of hole clearance on winding temperature

Figure 18.  Influence of hole clearance on stator core temperature

本文采用CFD的方法对半直驱永磁风力发电机三维温度分布规律及发电机散热效果影响因素进行研究，得到的主要结论为：

1）本文的仿真计算结果与实验结果误差小于5.1%，证明了本文建立的三维流动传热模型的准确性，这为后续的发电机设计和散热评估提供帮助。

2）发电机绕组、定子铁芯的最大温度出现在中层区域，最低温度出现在外侧两端，绕组温度最大温差达28.1 ℃，定子铁芯最大温差达53.1 ℃，工艺条件允许的情况下，冷却水管位置应尽可能靠近绕组，以带走更多的热量。

3）风冷系统中，增大总进风量对发电机散热效果改善显著，提高散热器功率更有利于发电机散热。降低进风温度可一定程度上改善发电机的散热效果，进风温度每降低5 ℃，最高温度降低约1.4 ℃。极限工况下，发电机进风温度较高，可先对热风进行冷却处理，使进入发电机内的空气满足温度要求，以降低发电机热载荷。

4）水冷系统中，降低冷却水管进水温度对发电机散热效果影响显著，进水温度每降低5 ℃，最高温度降低约3.3 ℃。

5）4种冷却液中，水的冷却效果最好，乙二醇次之。乙二醇的凝固点最低，抗冻性能好，适用于低温机型的冷却，水、丙二醇、乙醇可作为常温机型的冷却液使用。

6）管孔间隙极大地阻碍了冷却水管和定子之间的热交换。在定子组装过程中，在冷却水管表面涂抹导热性能较好的材料再进行装配，降低冷却水管与定子铁芯之间的热阻，增强冷却水管的换热效率。